[ICLR 2018] Active Learning For Convolutional Neural Networks: A Core-Set Approach

안녕하세요, 허재연입니다. 이제 슬슬 논문 읽는 분야를 Representation Learning에서 Active Learning(AL)으로 옮기려 하고 있습니다. 앞으로 한동안은 AL, MAE 관련 리뷰를 작성하지 않을까 싶습니다. 제가 AL의 개념을 아직 잘 알지는 못하고 컨셉 정도만 이해하고 있어서 부지런히 follow-up 해야 할 것 같습니다. 그런 의미에서 이번에는 AL에 대한 간략한 소개와 논문 하나를 다루고자 합니다. 이 논문은 제가 처음 읽어보는 AL 논문인데요, 타 AL 논문 대비 인용수가 높아서 선정했습니다. 이것 저것 찾아보니 이 논문이 AL 분야의 baseline으로 자주 등장하기도 하네요. 우선적으로 읽으면 좋을 것 같아서 덥석 읽기 시작했는데, 어려워서 디테일까지 완전히 이해하지는 못한 것 같습니다. 그래도 함께 살펴보면서, 나중에 다시 읽어봤을 때는 온전히 이해할 수 있기를 기대해야겠네요.

Preliminary

우선 AL이 무엇인지부터 간단히 짚고 시작하겠습니다. Active Learning은 데이터 부족 이슈를 극복하기 위해 연구되고 있는 분야들 중 하나입니다. self-supervised learning이 unlabeled data를 이용해 어느 정도 데이터의 표현력을 확보하는 것을 목표로 하고, semi-supervised learning이 적은 수의 labeled data를 이용해 학습하고자 한다면, AL은 대규모 unlabeled data를 가지고 있지만 (annotation cost의 부족으로)한정된 개수의 데이터만 annotation 할 수 있을 때, annotation 효용이 높은 데이터를 선별하는 방법을 연구하는 분야입니다.

수능을 코앞에 둔 고3 학생에게는 학교 교과서를 가지고 공부하는 것보다는 해당 학생에게 적절한 난이도의 맞춤형 문제(실전 모의고사라던지)를 푸는 것이 효율이 좋겠죠? 당연히 전 세계의 모든 문제를 다 풀어보고 수능을 보면 좋겠지만, 학생에게는 시간이라는 자원이 한정되어 있으니까요. AL은 이 학생이 당장 풀어보면 효율이 좋을 문제를 선별하는 것에 비유할 수 있겠습니다. AL 연구자들은 labeling cost가 한정되어 있는 상황에서 모델에게 학습 효율이 좋은 data를 선별하고 싶습니다. 그럼 학습 효율이 좋은 데이터란 무엇이고, 이 데이터를 어떻게 선별할 것인가? 라는 질문에는 크게 두 가지 연구 갈래가 있다고 답변 드릴 수 있겠습니다. 1.uncertainty 기반 방법과 2. diveristy 기반 방법입니다.

1. uncertainty 기반 방법은 ‘모델이 정답을 맞추기 어려워하는 데이터가 바로 학습 효율이 높은 데이터일 것이다’ 라는 관점에서 문제를 해결하고자 합니다. 고3의 예시를 다시 들어보자면, 수능 수학 1~2등급 수준의 학생들의 입장에서 수능 보기 직전 시기에 2,3점짜리 쉬운 문제만 푸는 것보다는 고난도 킬러 문항을 집중적으로 공략 하는 것이 공부 효율이 좋겠죠? uncertainty 기반 방법론에서는 너무 쉬운 데이터보다는 모델에게 적당히 어려운 데이터를 학습에 중점적으로 이용하려고 합니다. 편의를 위해 classification task를 예로 들어보자면, top1 confidence가 낮거나 decision boundary에 근접한 데이터를 ‘모델이 어려워 하는 데이터’ 라고 볼 수 있으므로, 이런 데이터를 중점적으로 labeling하려고 합니다. 다만, 모델이 어려워하는(decision boundary 근처에 있는) 데이터만 추출하다 보면 데이터 분포가 다양하지 못하게 될 수 있습니다.

2. diversity 기반 방법은 전체 dataset을 대표할 수 있는 subset을 추출하고자 합니다. uncertainty 기반 방법의 약점인 ‘데이터셋의 전체 분포를 반영하지 못하고 decision boundary 근처 데이터로 편향이 일어나는 문제’를 걱정할 필요가 없겠죠. 이 방법은 데이터셋 전체 분포를 잘 반영하는 데이터를 추출해서 학습하는 것이 모델에게 데이터를 잘 학습 시키는 방법이라는 관점에서 문제를 해결하려고 합니다. 오늘 리뷰하는 이 논문이 diversity의 관점에서 딥러닝 모델을 활용한 연구라고 보시면 됩니다.

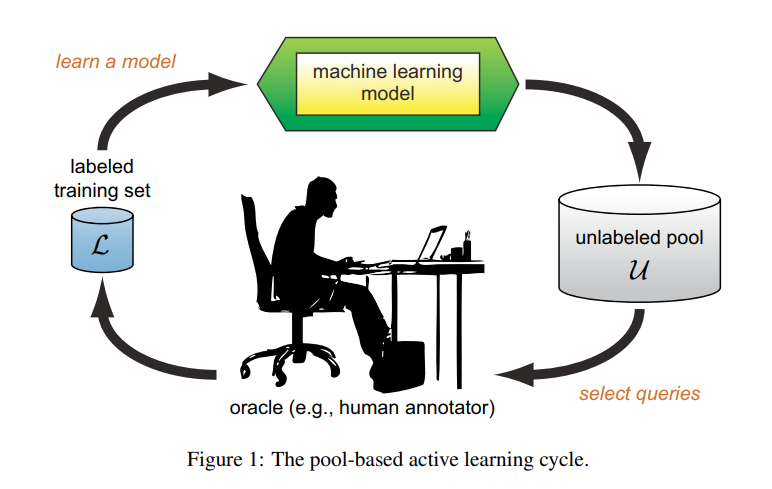
AL의 학습 사이클에 대해 살펴보겠습니다. AL은 처음에 소량의 labeled training set을 가지고 시작합니다. 이 소량의 데이터 셋을 가지고 AL 모델을 학습시킨 다음에 이 모델을 이용해 unlabeled pool에서 labeling할 데이터를 선별합니다. 선별된 unlabeled data는 human annotator(oracle)이 직접 labeling한 다름 labeled training set에 추가합니다. 이제 이 labeled pool로 AL 모델을 다시 학습시키고.. 이 사이클을 반복하게 됩니다. 초기 set을 이용해 맨 처음 AL 모델이 학습하고 데이터를 sampling하게 되니 초기 set을 어떻게 선별하는지가 이후 성능에 큰 영향을 미치게 됩니다.

이정도면 AL에 대한 큰 그림이 그려졌을 것이라 생각됩니다. 논문 리뷰 시작하겠습니다.

Abstact

CNN은 대규모 labeled dataset을 이용해 딥러닝 모델을 학습시키는 보편적인 방법으로 수많은 recognition, learning task에서 상당히 성공적으로 적용되어지고 있습니다. 하지만, 대규모 labeled dataset을 확보하는 것에는 너무 비용이 많이 들기 때문에 이 방법을 실제로 적용하기에는 상당히 제한적입니다. 저자들은 기존의 heuristic active learning 방법들이 CNN에 적용하기에는 효율적이지 못하다는 점을 지적하는데요, 기존의 AL learning은 instance 단위로 sampling하는데 반해 CNN은 batch 단위로 학습하기 때문이라고 합니다.

이런 한계점에서 저자들은 AL 문제를 기존 방법들로 풀어나가지 않고, 주변 데이터를 날 나타낼 수 있는 데이터를 선별하는 ‘Core-Set selection’문제로 정의했다고 합니다. (point set을 잘 선별하는 방법이라고 생각하시면 될 듯 합니다)

Introduction

CNN은 image classification, object detection, seene segmentation 등 수많은 컴퓨터비전/패턴인식 연구 분야에서 상당히 성공적인 모습을 모여주었습니다. 이런 보편적인 성공에도 불구하고 CNN에는 큰 단점이 있습니다. 수많은 파라미터를 학습하기 위해 대규모의 labeled data가 필요한 것입니다. 데이터가 많아진다고 CNN의 정확도가 포화되는 경우는 많지 않기 때문에 대부분 labeled data가 많을 수록 학습에 더 유리합니다. 따라서 더 많은 데이터를 수집하고자 하는 시도가 계속되어 왔습니다. 하지만 데이터를 수집하고 labeling을 하는 것은 시간도 많이 들고 비용도 상당히 많이 듭니다. 이러한 제한상황에서 ‘고정된 라벨링 예산이 주어졌을 때 가장 높은 정확도를 얻을 수 있도록 라벨링할 데이터를 선택하는 최적이 방법은 무엇일까?’라는 화두가 던져졌고, 이 질문을 해결하기 위한 일반적인 방법으로 Active Learning이 제시되었습니다.

Active learning의 목적은 unlabeled data point pool에서 정확도를 최대화 하기 위해 라벨링할 데이터를 효율적으로 찾아내는 것입니다. 논문이 제안될 당시 까지 수많은 휴리스틱 방법이 제안되었다고 하는데, 저자들은 이런 휴리스틱한 방법들이 batch sampling/acquisition으로 인해 CNN에서 사용하기에는 (비효율적이기 때문에)부적절함을 지적합니다. 기존의 고전적인 방법에서는 active learning 알고리즘이 일반적으로 각 iteration마다 하나의 data point를 추출했다고 하네요. 하지만 이런 방법들은 1. 하나의 data point로는 local optimization 방법에 통계적으로 유의미한 영향력을 가지기 힘들고 2.각 iteration에서 수렴까지의 과정이 필요하므로 label을 일일히 쿼리하는것이 어렵기 때문에 각 iteration에서 어느 정도는 큰 subset에 대해 label을 쿼리할 필요가 있다고 합니다.

저자들은 Active Learning을 batch sample이 필요한 케이스에 알맞게 변형하기 위해 AL을 ‘core-set selection’ 문제로 정의하기로 했다고 합니다. Core-set selection 문제는 선택된 집합을 통해 학습된 모델이 전체 데이터셋에서 학습된 것과 경쟁력을 가질 수 있도록 작은 부분 집합을 선택하는 것을 목표로 합니다. 이 과정에서 label을 사용할 수 없으므로 라벨 없이 core-set selection을 진행합니다. Core-set을 통해 추출한 sample들은 전체 dataset을 대표할 수 있어야 합니다.

Method

AL은 다음 future expected loss를 줄이고자 합니다.

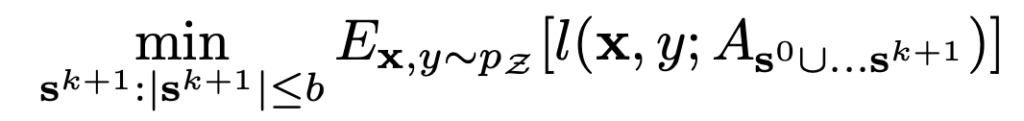
여기서 S0은 초기 labeled pool을, S1은 1번의 iteration으로 뽑은 subset입니다. b(budget)은 뽑아야 할 data point 수를 의미합니다. 저자들은 batch 단위 학습을 효율적으로 하기 위해 위 AL loss의 upper bound를 다음과 같이 다시 정의합니다.

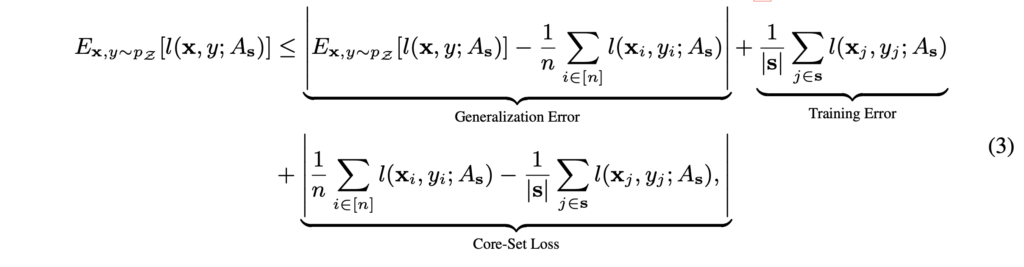
저자들은 이 식에서 CNN 동작을 가정할 때, CNN은 매우 낮은 training error와 다양한 visual problem에서 준수한 generalization error를 보여줌이 이미 증명되었다고(Xu&Mannor2012) 하며 core-set loss에 집중합니다. core-set 이외의 loss값은 CNN의 성능으로 0에 가까워짐이 알려졌으므로 core-set loss만 잘 다루면 된다는 흐름입니다. 이를 통해, 저자들은 learning problem을 다음과 같이 재정의합니다.

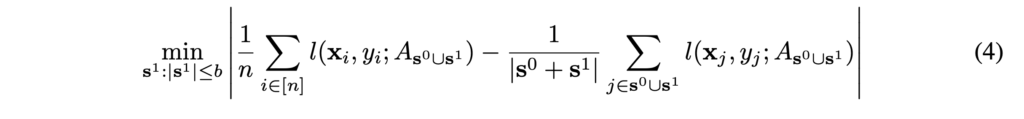
(4)번 수식에 대한 최적화는 전체 라벨을 모르기 때문에 directly computable하지는 않는다고 합니다. 따라서, 저자들은 여기에 최적화가 가능한 목적함수의 upper bound를 이용합니다. 여기 장황한 설명이 나오긴 하는데 다음 그림으로 요약할 수 있습니다.

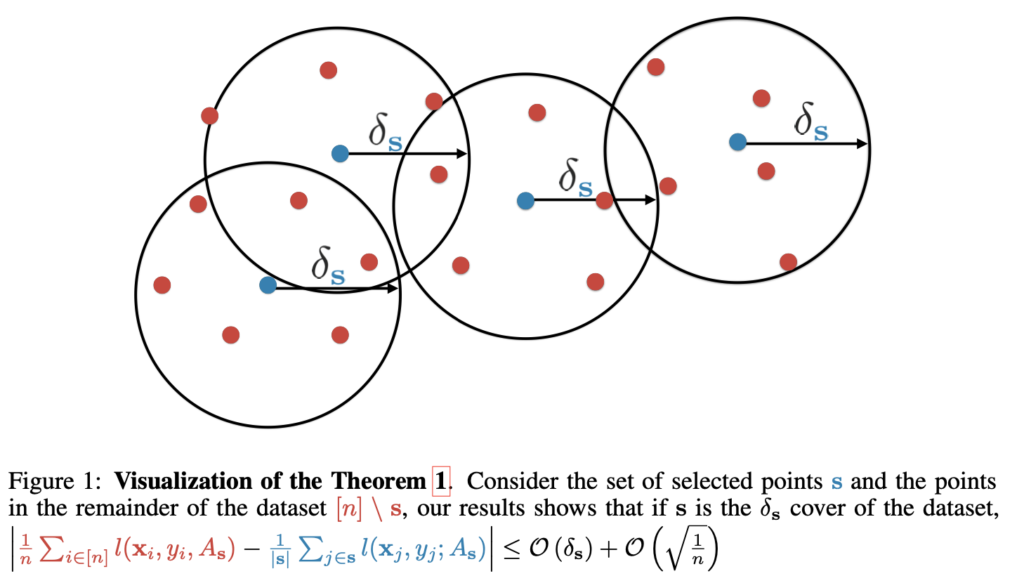
저자들은 여기서 적절한 core-set을 찾으려 하는데, 적절한 core-set을 찾기 위해서는 그림에서 빨간 점에 해당하는 데이터를 모두 커버할 수 있는 적절한 거리인 δs를 구하고, δs에 해당하는 적절한 core-set(그림에서는 파란색 점)을 찾으면 됩니다. 모델이 select한 점을 파란색 점이라고 하면, 이 파란 점을 중심으로 δ반지름의 원들을 그린 다음 원들을 다 합집합 했을 때 전체 distribution을 커버할 수 있을 것입니다. 이 때 반지름 δ를 minimize해서 파란 중심 점들을 골라내는 optimization을 합니다. δ가 minimize된 파란 점들이 데이터 전체를 커버하는 대표점들, core-set이 됩니다.

저자들은 이 core-set 문제 해결을 위해 두 가지 알고리즘(k-center greedy, robust k-center)을 제안합니다.

K-center greedy

저자들은 loss함수의 upper bound에 대해 core-set selection 문제가 k-center problem과 동등하다고 합니다(wolf2011). 데이터 포인트와 최근접 센터 사이 최대 거리를 최소로 만드는 b center point를 찾는 것이라고 합니다.

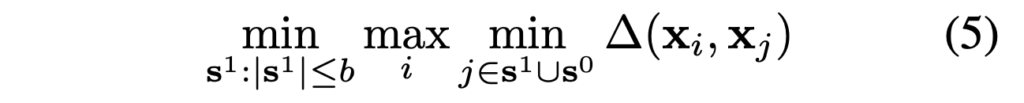
Robust k-center

robust k-center는 k-center problem을 outlier에 보다 강건하게 하기 위한 알고리즘입니다. 이상치 개수가 Ξ를 넘어가지 않게 하고, lower bound와 몇 제한을 걸였습니다.

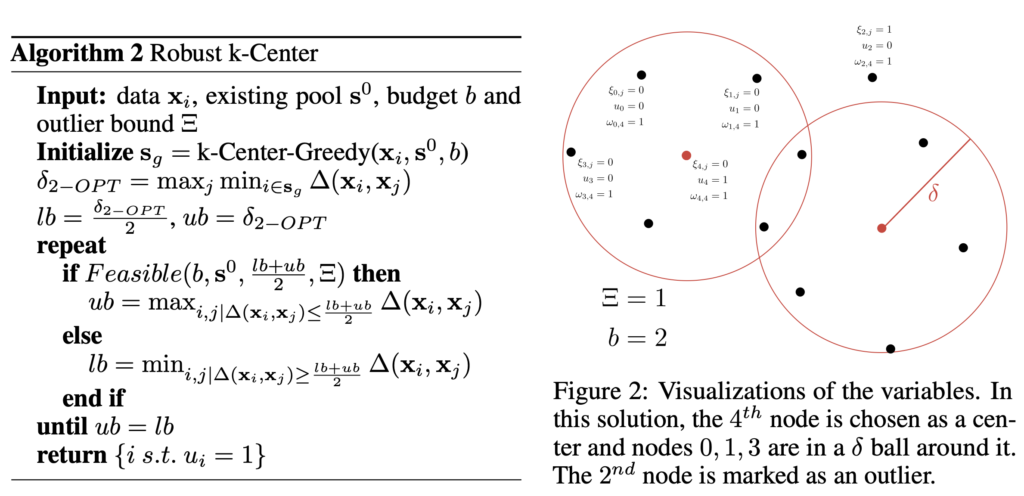
몇가지 구현 세부사항을 살펴보면, 거리는 마지막 fc 이후에 l2 distance를 적용하였고, VGG16을 기본 백본으로 사용하였다고 합니다. 최적화에는 RMSProp optimizer(lr=1e-3)을 사용했다고 합니다.

Experiments

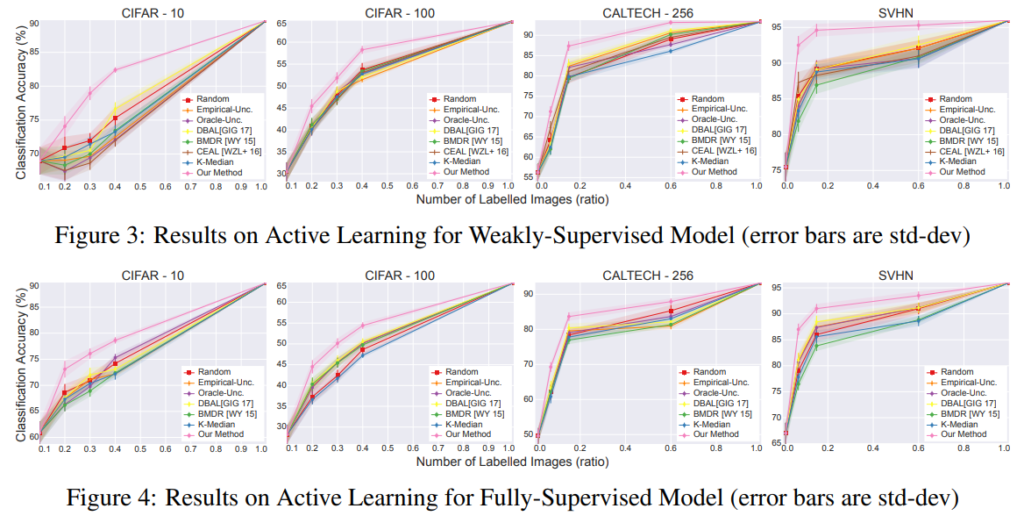
실험은 3가지 데이터셋(CIFAR, CALTECH101, SVHN)에 대해서 수행되었습니다. 기존의 다양한 active learning 방법론들과의 비교 실험이 수행되었습니다. 가로축은 샘플링 비율이므로, 1.0에서는 모든 데이터를 사용한 학습입니다. 모든 성능이 1.0으로 가면서 동일해지겠죠)저희가 집중에서 볼 지점은 sampling rate가 낮은 0.1~0.8 정도입니다. 어떤 방법으로 해당 비율만큼 샘플링했을 때 기존 대비 얼마나 성능이 높은지를 알 수 있습니다. table에서도 나와 있듯이, 기존 방법론들을 누르고 SOTA를 찍은 것을 알 수 있습니다.

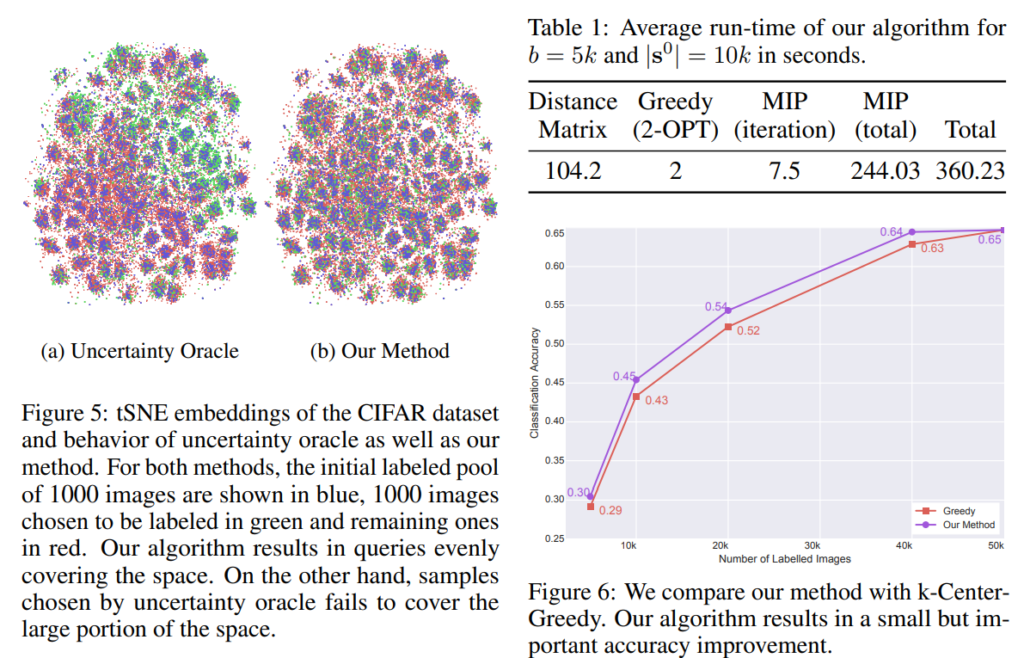
Fig5의 왼쪽은 t-SNE 임베딩을 나타낸 것입니다. 파란색은 초기 labeled 데이터, 초록색 점은 AL을 통해 선택한 데이터, 빨간 점은 뽑히지 않은 데이터 입니다. Core-Set 방법은 골고루 퍼져 있는데 반해, uncertainty 기반 방법은 색깔이 치우쳐져 있는 것을 확인할 수 있습니다. 모델 학습 시 치우쳐진 데이터로 학습하게 될 것입니다. 일반화 성능이 약화되겠죠. (diversity라고 단점이 없지는 않습니다. 모델이 어려워하는 결정 경계 부근의 정보를 적게 가지고 있고, outlier에 취약해집니다.)

Table 1에서는 알고리즘 실행 시간이 비교되었는데요, MIP가 상당히 많은 시간을 소모하는것을 확인할 수 있습니다. 시간을 줄일려면 이 부분을 해결해야 겠네요. 논문에서는 감안할만한 속도라고 언급합니다.

Conclusion

해당 논문에서 저자들은 CNN을 위한 Active Learning을 연구했습니다. 실험적으로 고전적 uncertainty 기반 방법이 batch sampling으로 인한 correlation으로 CNN에 적용하기에는 제한적이라는 것을 보여주었습니다. 이에 저자들은 AL 문제를 core-set selection 문제로 재정의하고 CNN을 위한 core-set 문제를 연구하였고, 실험 결과를 통해 해당 방법의 성능을 입증하였습니다.

AL에 대해 제가 아는 바를 최대한 담아보려고 했는데요, 아직 공부가 얕아 뭔가 빈약한 느낌이 들기도 하고.. 차차 채워 나가야 할 것 같습니다(논문이 citation을 많이 하는데 각 인용에 대한 이해가 전무하다보니 깊게 이해하진 못한 것 같습니다..). 혹시라도 수정할 사항이나 피드백 있으시다면 남겨주시면 감사하겠습니다.