[CVPR 2023]Object Pose Estimation with Statistical Guarantees: Conformal Keypoint Detection and Geometric Uncertainty Propagation

제가 이번에 리뷰할 논문은, 6D Pose Estimation의 예측값의 신뢰도를 고려하기 위해 uncertainty 개념을 도입한 방법론입니다.

---

Abstract

2-stage 방식의 object estimation은 semantic keypiont를 예측한 뒤, reprojection error가 줄어들도록 pose를 예측하는 방식입니다. 기존 연구들은 좋은 성능을 보이기는 하였으나, 예측 결과를 보장할 수 없다는 문제가 있었습니다. 이에, 본 논문에서는 conformal keypoint detection과 geometric uncertainty propagation이라는 두가지 요소를 추가함으로써, 2-stage 방식에 증명과 계산이 가능한 worst-case error bound를 가지는 최초의 pose estimator를 제안합니다. conformal keypoint detection은 inductive conformal prediction의 통계적인 장치를 이용하여 heuristic하게 keyhpoint를 감지하고, 이를 사용자가 설정한 확률로 GT를 포함하는 원이나 타원형태의 예측 집합으로 변환합니다. keypoint의 기하학적인 제약조건을 6D pose estimation으로 전달하는 Geometric uncertainty propagation은 동일한 확률로 GT pose의 적용 범위를 보장하는 PURSE(Pose UnceRtainty SEt)로 들어갑니다. 그러나 PURSE는 convex한 집합이 아니기 때문에 직접적으로 pose와 uncertainty를 예측할 수 없었다는 문제가 있습니다. 따라서 본 논문에서는 평균 pose를 계산하고, 평균 pose와 GT pose 사이의 error 상한인 최악의 경우에 semidefinite relaxtion을 적용하기 위해 RANSAG(RANdom SAmple averaGing)를 개발하였습니다. 본 논문은 LineMOD Occlusion 데이터를 이용하여 (1) PURSE가 타당한 확률로 GT를 포함한다는 것을 증명하고, (2) 최악의 error bound에서 정확한 uncertainty 정량화 수치를 제공하는 것을 확인하였으며, (3) 평균 pose는 sparse keypoint기반의 대표적인 방법론과 비교했을 때 유사하거나 더 좋은 성능을 달성함을 보였습니다.

Introduction

6D Pose Estimation은 증강현실이나 자율주행, 로봇 조작 등 광범위한 활용이 가능하다는 점에서 컴퓨터비전에서 중요한 문제입니다. object pose estimation은 대부분 2-stage 방식으로 구성되며, 이러한 2-stage 방식은 keypoint를 감지하고, PnP를 이용하여 reprojection error가 감소하도록 pose를 추정하는 방식입니다. 그러나 6D Pose Estimation의 활용은 안전이 굉장히 중요하여 알고리즘의 증명이 요구되지만, 기존의 2-stage 알고리즘은 다음의 3가지 challenge로 인해 대부분 성능을 보장할 수 없었습니다.

< Challenges >

• C1: 예측된 Keypoint가 GT와 유사할 것이라는 보장이 어려움
• C2: outlier를 피하고자 2번째 단계(pnp로 pose추정)에 robust한 estimation을 적용하지만, 이로인해 nonconvex하게 최적화됨.
  (RANSAC과 같이 빠르고 heuristic한 방법론이 널리 사용되지만, 이는 global 최적을 보장할 수 없고, 자주 예고 없이 실패함)
• C3: 추정치에 대한 정확한 uncertainty 정량화 수치가 없으며, 특히 추정치와 GT 사이의 worst-case error bound 공식이 없음

최근 연구들은 RANSAC의 global 최적화를 위한 연구를 진행하여 C2 문제를 해결하였지만, keypoint를 신뢰할 수 없는 경우, 최적의 pose가 GT pose와 떨어져있을 수 있으므로, 여전히 정확한 예측을 보장할 수 없다는 문제가 있습니다.

Contributions

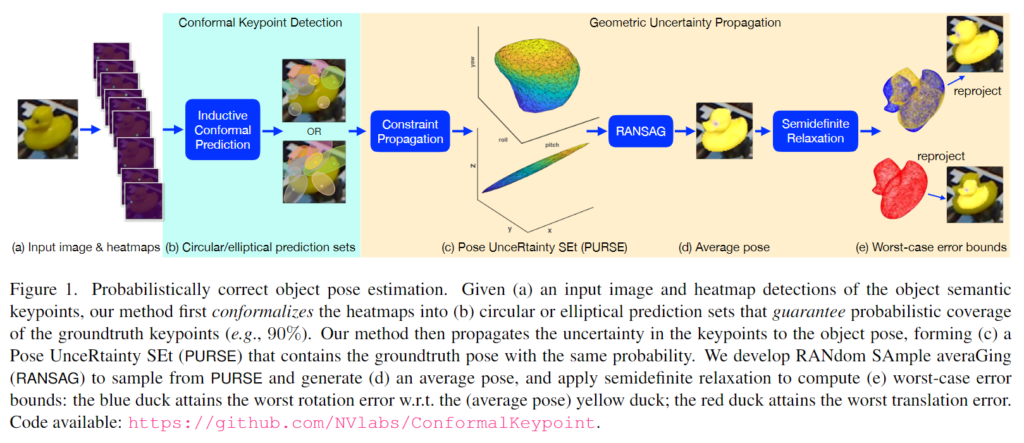
본 논문은 통계적으로 보장이 가능한 2-stage object pose estimation 프레임워크를 제안합니다. 주어진 입력 이미지가 네트워크를 통해 object의 keypoint heatmap을 생성한 뒤(Fig. 1(a)), conformal keypoint detection과 geometric uncertainty propagation을 거치게 됩니다. inductive conformal prediction의 통계적 메커니즘을 적용하여 heatmap을 원형이나 타원형의 prediction set으로 공식화하여 사용자가 설정한 확률로 GT keypoint의 범위를 보장합니다(Fig. 1(b)). 이를 통해 단순하고 일반적인 방식으로 keypoint 예측 오류를 제한하여 C1 문제를 해결하고자 합니다. 또한, keypoint prediction set이 주어졌을 때, keypoint에 대한 제약 조건을 pose의 제약조건으로 재구성하여 동일한 확률로 GT pose의 범위를 보장하는 PUSE를 도출합니다(Fig. 1(c)). PURSE는 대략적인 non-convex 집합이므로 pose와 uncertainty를 직접적으로 구할 수 없습니다. 따라서 RANSAG를 개발하여 평균 pose를 계산하고(Fig. 1(d))., semi-definited relaxtion을 도입하여 평균 pose와 GT 사이의 최악의 error 상한을 두게 됩니다(Fig. 1(e)).

본 논문의 제안사항은 LineMOD Occlusion 데이터를 이용하여 검증되었으며,

1. PURSE가 실제로 사용자가 설정한 확률로 GT Pose를 포함한다는 것을 실험적으로 보이고,
2. worst-case에 대한 error bound가 적절함을 증명하였고,
3. RANSAG로 구한 평균 poes의 정확도를 다른 sparse keypoints 방법론과 비교하여 유사하거나 더 좋은 성능을 보였습니다.

1. Inductive Conformal Prediction

관측값 x_i ∈ \mathcal{X}와 라벨 y_i ∈ \mathcal{Y}로 이루어진 집합 \{ z_i = (x_i ,y_i) \}^l_{i=1} 이 주어졌을 때, z_i ∈ \mathcal{Z} := \mathcal{X}⨉\mathcal{Y}(z는 x,y의 외적)이고, 알려지지 않은 분포를 가진 \mathcal{Z}로부터 inductive conformal prediction(ICP)는 prediction 집합인 F^{\epsilon}(x) ⊆\mathcal{Y}를 생성합니다. 이때, prediction 집합은 0< \epsilon <1 의 범위인 오차비율로 파라미터화 되었으며, exchangeability 조건(아래의 Theorem 1에서 구체적으로 설명합니다)을 만족하는 새로운 샘플 z_{l+1} = (x_{l+1},y_{l+1})가 주어졌을 때, 아래의 식을 구할 수 있습니다.

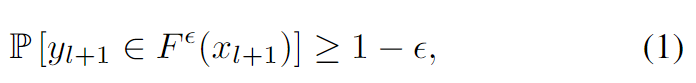
즉, prediction set F^{\epsilon}에 실제 라벨 y_{l+1} 이 포함될 확률이 최소한 1-\epsilon 이상이라는 것을 보장한다는 것입니다.

Training

데이터셋을 학습 셋 \{ z_1, ..., z_m \}과 calibration set \{ z_{m+1}, ..., z_l \}로 나누고, calibration set의 크기는 n= l-m 라 합니다. 어떤 구조를 가지는 딥러닝 네트워크인 예측 함수 f: \mathcal{X→\tilde{Y}} 를 앞서 나눈 적절한 m개의 학습 셋을 이용하여 학습합니다. 예측 공간 \tilde{\mathcal{Y}} 는 label 공간 \mathcal{Y} 와 동일할 수 있고, 추가적인 정보를 포함할 수 있습니다. 여기서 추가적인 정보라 표현하였는데, softmax나 heatmap을 이용한 keypiont를 이용함으로서 불확실성에 대한 정보를 포함하고있다는 것입니다.

Conformal calibration

nonconformity 함수를 S: \mathcal{Z}^m ⨉ \mathcal{Z}→\mathbb{R} 로 정의하고, nonconformity 함수를 통해 주어진 샘플 z=(x,y)가 학습 set과 얼마나 일치하는 지를 측정합니다. S는 학습된 예측 함수 f를 이용하며, 아래의 식으로 표현할 수 있습니다.

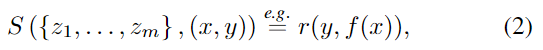
이때, r: \mathcal{Y}^m ⨉ \mathcal{Y}→\mathbb{R} 은 label y와 예측값 f(x)의 불일치 정도를 측정한 것이고, (x,y)가 train set과 일치하지 않을 경우 오차가 커지도록 r(y,f(x)) = |y-f(x)| 와 같은 형태로 설계할 수 있습니다. 또한, 식 (2)는 샘플 \{ z_i \}^m_{i=1} 와 r 에 따라 달라지며 도메인 특정 지식을 통합할 수 있는 f를 식에 활용하므로 이러한 정보를 포함할 수 있다는 장점이 있습니다.

그 다음, calibration set에 대한 nonconformity score를 \alpha_i = r(y_i,f(x_i)), i=m+1, ...,l 로 계산하고, 내림차순으로 정렬합니다. ( \alpha_{\pi (1)} ≥ ... ≥ \alpha_{\pi (n)}, 이때, (\pi (i) ∈ \{ m+1, ..., l \} ) 로 정렬된 결과에 대해 재인덱싱을 해주는 것)

Conformal prediction

label값을 모르는 새로운 샘플 x_{l+1}과 사용자가 정의한 확률값인 \epsilon ∈(0,1) 가 주어졌을 때, inductive conformal prediction (ICP) set은 아래의 식(3)으로 계산되며, 이때 \alpha^{y} = r(y, f(x_{l+1})) 는 GT label이 y인 새로운 샘플에 대한 nonconformity score입니다.

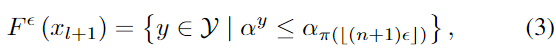
즉, ICP set의 output(식(3))은 새로운 샘플의 nonconformity score가 (⌊( n+1 )\epsilon⌋ 번째로 큰 nonconformity score값 \alpha_{\pi (⌊( n+1 )\epsilon⌋ )} 보다 크지 않도록 합니다. (⌊.⌋는 내림을 의미)

Theorem 1 (Validity of ICP Coverage)

z_{m+1}, ..., z_{l}, z_{l+1} = (x_{l+1},y_{l+1})이 exchangeability하고 분포는 불변일 경우 아래의 식을 만족합니다.

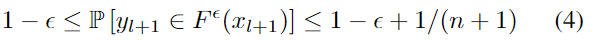
또한, calibration set을 조건으로 하고, h= ⌊ (n + 1) \epsilon ⌋ (⌊.⌋는 내림을 의미)라 하면, 아래의 식을 만족합니다.

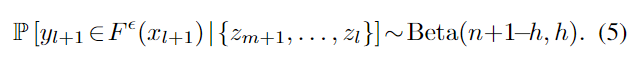
[Theorem 1에 대한 설명]

1. 여기서 exchangeability 조건에 대해 설명하자면, 저자들은 교환 가능하다는 것이 각 요소가 독립적이라는 것 보다는 완화된 조건이라 합니다.
   • 그러나, calibration set 이 연속된 단일 비디오 sequence일 경우에는 시간축으로 모두 관련되어있기 때문에 exchangeability를 만족하지 못하고 앞서 정의한 식에 부적절하다고 합니다.
   • 본 연구에서 사용한 LineMOD Occlusion은 단일 비디오 sequence가 아니므로 위의 z_{m+1}, ... , z_{l+1}이 exchangeability하다는 가능하다는 조건을 충족한다고 합니다.
2. 식 (4)의 하한은 exchangeability를 통해 직관적으로 증명이 가능합니다.
   • 새로운 샘플에 대한 nonconformity score \alpha_{l+1} :=r(y_{l+1}, f(x_{l+1}) 가 calibrate set의 nonconformity score와 exchangeable 하므로, nonconformity score \{ \alpha_{\pi (i)} \}^n_{i=1}사이에 포함될 확률이 모두 동일합니다.
   • 즉, \mathbb{P}[\alpha_{l+1} ≤\alpha_{\pi (⌊( n+1 )\epsilon⌋ )} ] = 1 - ⌊( n+1 )\epsilon⌋ /(n+1) ≥ 1 - \epsilon 가 됩니다.
3. 식(4)의 보장 확률은 calibration set의 랜덤성에 비해 미미하여,
   랜덤으로 무한개의 calibration set을 선택하였을 때, 평균적인 보장 범위는 1-\epsilon 로 수렴합니다.
   • 그러나, 이는 calibration set에서 구할 수 있는 보장 범위는 Beta 분포 식(5)에 따라 변동하는 랜덤 변수라는 것을 의미합니다.
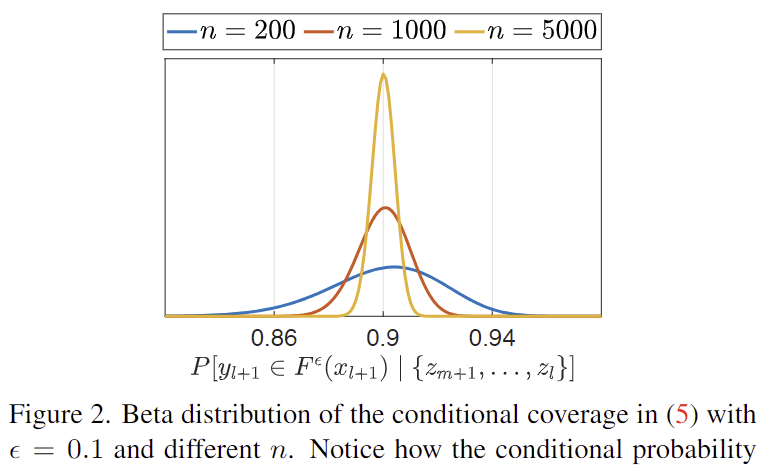
   • 아래의 그림 2는 \epsilon =0.1 일 때, 다양한 크기의 calibration set에 따른 Beta 분포를 나타낸 것으로 n 이 커질수록 보장 범위가 1-\epsilon 에 집중된다는 것을 확인할 수 있습니다.
   • 또한, n=200으로 작은 calibration set을 사용하여 실험을 하더라도, 보장 범위가 1-\epsilon 에 가깝고, 대부분이 더 높은 확률을 가진다는 것을 확인할 수 있습니다.

2. Conformal Keypoint Detection

해당 파트에서는 앞서 설명한 ICP를 이용하여 의미론적인 keypoint detection에 적용합니다.

Setup

x ∈\mathbb{R}^{H⨉W⨉3} 를 RGB 이미지라 하고, \mathbf{y}=(y_1,...,y_K) ∈\mathbb{R}^{2} ⨉ ... ⨉\mathbb{R}^{2}:= \mathcal{Y} 는 K개의 semantic keypoint 위치라 할 때, 주어진 데이터셋 \{ z+i := (x_i, \mathbf{y}_i) \}^l_{i=1} 를 m개의 적절한 training set과 n개의 calibration set으로 분할합니다.

Training

heatmap을 이용하는 기존 연구[1,2]를 따라서 prediction function을 설정해줍니다. 이 예측 함수는 x를 입력으로 하고, 입력에 대해 heatmap 집합 \mathbf{f}(x) = (f(x)_1, ..., f(x)_K)을 반환합니다. 이때 f(x)_k ∈ \Delta^{HW} := \{ v ∈ \mathbb{R}^{HW}_+ | \Sigma^{HW}_i v_i= 1 \} 로, k번째 keypoint가 존재할 위치를 확률분포를 이용하여 나타냅니다.

편의를 위해 x의 j번째 픽셀 위치는 q^j ∈ \mathbb{R}^2 로 나타내고, q^j 에 있는 k번째 keypoint의 확률은 f(x)^j_k ∈ \mathbb{R}_+ 로 표현합니다. f(x)_k 를 내림차순으로 정렬하고 \sigma_k 를 이용하여 재인덱싱을 하면 f(x)_k^{\sigma _x (1)} ≥ ... ≥ f(x)_k^{\sigma _x (HW)} 로 표현이 가능합니다.

**[1]Georgios Pavlakos., et al, “6-DoF object pose from semantic keypoints.” ICRA., 2017.

**[2]arl Schmeckpeper., et al, “Semantic keypoint-based pose estimation from single RGB frames” J.of Field Robotics., 2022.

Conformal calibration

nonconformity 함수를 아래의 식 (6)으로 설계하였습니다.

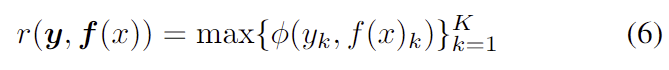
각 keypoint의 점수를 \phi 로 구한 뒤, 가장 큰 점수를 선택합니다. 이 식은 f가 최악의 keypoint를 검출하는 경우를 고려합니다. \phi 는 아래의 두가지로 디자인을 하였습니다.

[\phi 디자인 고려사항]

1. Peak

• p_k = f(x)^{\sigma _k(1)}_k 로, k번째 heatmap의 최대 확룔을 나타내고
• q_k = q^{\sigma _k(1)}는 최대 확률을 가지는 픽셀이 위치

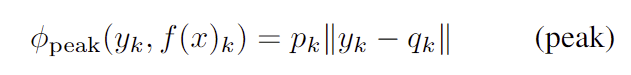
peak는 실제 keypoint 위치와 가장 가능성이 높은 keypoint 위치 사이의 오류를 계산하고 peak 확률만큼 오류를 조정합니다. peak는 네트워크가 완전히 잘못될 경우(|| y_k - q_k ||, p_k가 모두 클 경우) 큰 값을 가져 nonconformity를 나타내며 이를 통해 샘플이 매우 부적합하다는 것을 표현할 수 있습니다.

2. Covariance

• \bar{q}_k = \Sigma ^J_{j=1} f(x)^{\sigma _k(j)}_k q^{\sigma _k(j)}로 keypoint k가 존재할 가능성이 높은 상위 J개의 예측 위치이며,
• \Sigma _k = \Sigma^J_{j=1} f(x)^{\sigma _k(j)}_k · (q^{\sigma _k(j)} - \bar{q}_k)(q^{\sigma _k(j)} - \bar{q}_k) ^T 를 공분산이라 할때

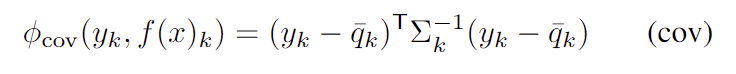
convariance를 고려하여 위의 식으로 디자인하였으며, 이는 GT y_k 로부터 J개의 상위 예측 keypoint 까지의 마할노비스 거리 제곱을 계산합니다. 마할노비스 거리가 클수록 heatmap f(x)_k 가 잘못되었음을 나타내고 따라서 더 높은 nonconformity를 의미합니다.

이처럼 (식 peak)와 (식 cov)를 이용하여 식(6)의 nonconformity score를 구할 수 있습니다.

Conformal prediction

오차비율이 \epsilon 이 주어졌을 때, 먼저 \alpha_{\pi (⌊( n+1 )\epsilon⌋ )} 를 구하고, ICP 집합의 정의 (식(3))와 nonconformity 함수 (식(6))에 따라 새로운 샘플 x_{l+1}의 output을 다음과 같이 구합니다.

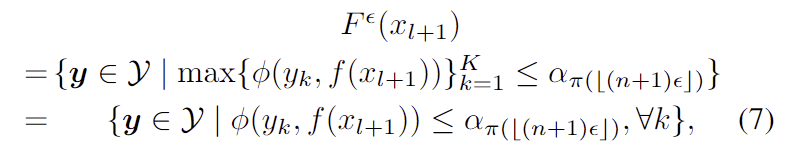
식(7)에 (식 peak)를 넣어 F^{\epsilon}_{ball} (x_{l+1}) 를 아래의 (식 ball)을 구합니다.

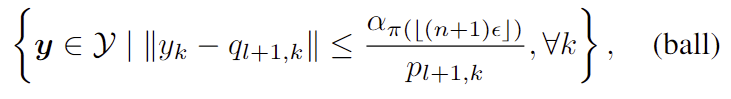
(식 ball)은 k번째 keypoint에 대해 가장 높은 확률을 가지는 q_{l+1,k} 가 중심이 되고 반경이 p_{l+1,k} 에 반비례하고 \alpha_{ \pi (⌊( n+1 )\epsilon⌋ )} 에 비례하는 ball로 정의됩니다.

유사하게 식 (7)에 (식 cov)를 넣어 F^{\epsilon}_{ellipse} (x_{l+1}) 를 구합니다.

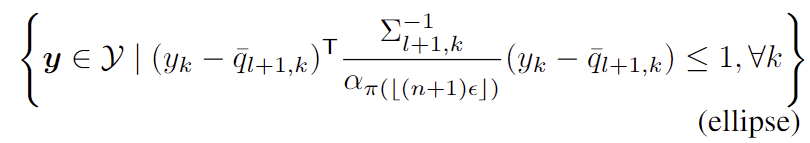
(식 ellipse)는 k번째 keypiont에 대해 \bar{q}_{l+1,k} 가 중심이 되고, det(\Sigma_{l+1,k}) 와 \alpha _{ \pi (⌊( n+1 )\epsilon⌋) }에 비례하는 몀ㄴ적을 갖는 ellipse(타원)으로 정의됩니다.

(식 ball)과 (식 ellipse)에서 (1) heatmap이 불확실 할 때 (peak확률이 낮거나 convariance의 determinant가 클 때) (2) calibration set에서 heatmap이 잘 작동하지 않을 때 nonconformity socre \alpha _{ \pi (⌊( n+1 )\epsilon⌋) }가 커지도록 설계하였습니다.

Connections to geometric vision

nonconformity 함수는 기하학적 vision의 residual 기능과 유사합니다. (식 peak)와 (식 cov)가 reprojection error와 유사한 기능을 하며, 식(6)의 max는 l_{\infin} 의 norm을 최적화하는 작업과 연관됩니다.

Outlier-robust nonconformity

nonconformity 함수 (식 (6))의 잠재적인 문제는 하나의 이상치가 score와 calibration quantile을 부풀려 prediction set에 영향을 줄 수 있다는 것입니다. (f가 k-1개의 keypoint를 정확하게 예측하고 하나만 잘못되더라도 문제가 발생) 이를 해결하기 위해 vision은 robust cost function을 이용하여 해결하고, 이에 대해 robustifiying에 대한 의문이 제기됩니다.

Proposition 2 (Invariance of ICP)

\rho 가 어떠한 단조증가함수(cost function으로 사용되는 l_1, Huber, Geman-McClure, Barron’s adaptive kerner을 표현한 것)라 할 때, calibration set과 오차 비율 \epsilon 을 수정한 nonconformity 함수는 아래의 식(8)로 나타낼 수 있습니다.

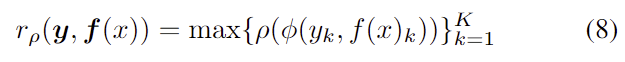
이를 통해 cost를 추가하더라도 개별적인 score를 강인하게 하여 ICP set이 변하지 않는다고 결론을 내렸습니다.

하지만 식(6)의 “max”연산을 변경할 경우 더 좋은 ICP set을 구할 수 있는지는 여전히 의문으로 남아있다고 합니다. max 대신 “ \Sigma “를 적용하고 Geman-McClure의 robust cost를 활용하여 \rho(\phi) = {{\phi ^2} \over{1+ \phi ^2} }, \phi = \phi_{peak} 로 설정하였을 때, ICP set은 아래의 식 (9)가 됩니다.

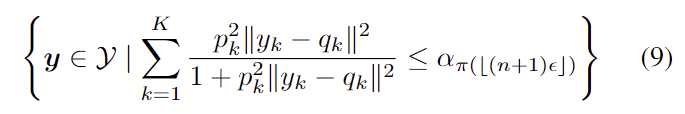
식 (9)는 직관적으로 해석이 어렵고, 다음 섹션에서 확인할 수 있듯이 pose정보에 불확실성을 전달할 수 있는 것은, max를 이용하였을 때 얻을 수 있는 ball과 ellipse 형태의 단순성이라고 합니다. (max를 \Sigma 로 바꾸는 (9)를 통해, 다른 연산이 더 잘 작동하는지는 확인하기 어렵다는 것을 보여준 것입니다.)

3. Geometric Uncertainty Propagation

heatmap을 정형화하면 실제 keypoint의 확률적 범위를 보장하는 keypoint 예측 set을 구할 수 있습니다. 예측 set인 (ball)과 (ellipse)를 통합하면 아래의 식 (10)으로 나타낼 수 있고

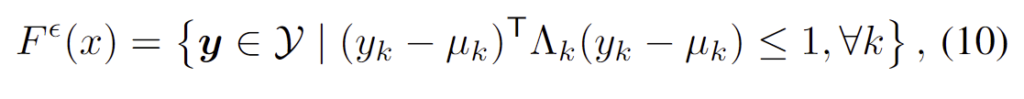
이때 (ball)과 (ellipse)에 따라 \mu , \Lambda 의 정의는 다음과 같이 달라집니다.

• (ball)일 경우
  • \mu = q_{l+1,k,} ,  \Lambda_k= { {p^2_{l+1,k}} \over {\alpha^2_{\pi (⌊( n+1 )\epsilon⌋) } }} \mathbf{I}_2
• (ellipse)일 경우
  • \mu = \bar{q}_{l+1,k,} ,  \Lambda_k= { {\Sigma ^{-1}_{l+1,k}} \over {\alpha^2_{\pi (⌊( n+1 )\epsilon⌋) } }} \mathbf{I}_2

[Why not uncertainty-aware PnP?]

pose 추정에서 가장 많이 사용되는 방식은 불확실성을 인식하는 PnP를 이용하는 것 입니다.

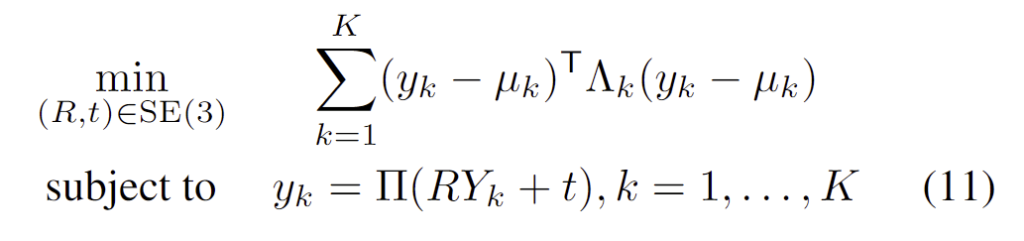
• Y_k ∈ \mathbf{R}^3, k=1,...,K : 3D 물체의 keypoint
• \Pi (.): camera projection

저자들은 PnP에 대하여 2가지 문제를 지적합니다.

1. non-convex한 SE(3) 제약과 다항식 \Pi(.) 로 인해 식(11)의 global한 해를 구하기 어렵다
2. 식(11)의 해를 구하는 것은 일반적으로 uncertainty에 대한 정량적 수치를 고려하지 않고, 하나의 pose를 추정하는 방식이다

이러한 특징에 의해 “최적의 pose와 비슷한 다른 최적의 pose는 없는지”와 “최적의 pose는 GT와 얼마나 가까운지”에 대한 답변을 해결되지 않았습니다. 이러한 PnP를 사용할 때의 문제점을 언급하며 저자들은 PURSE라는 새로운 방식을 제안합니다.

Pose UnceRtainty SEt(PURSE)

저자들은 PnP를 푸는 것이 아닌, ICP set의 불확실성을 객체의 pose로 전파할 수 있는 PURSE를 제안하였습니다.

Proposition 3 (PURSE)

GT pose s_{gt} = [vec(R_{gt}^T ; t_{gt}^T)] 라 할 때, GT keypoints \mathbf{y}=(y_1, ..., y_K)는 s_{gt} 가 pose uncertainty set에 속하는 경우에만 식(10)의 ICP set F^{\epsilon (x)} 에 해당합니다. pose uncertainty set은 아래와 같이 표현할 수 있습니다.

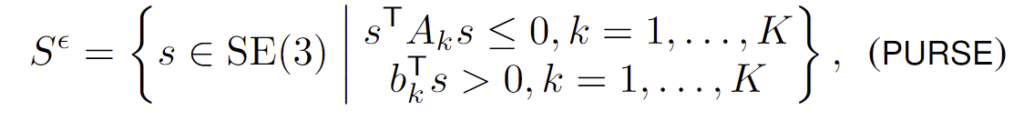
• 이때 A_k ∈ \mathbb{S}^{12}, b_k ∈ \mathbb{R}^{12}, k=1, ...,K 는 카메라의 intrinsics와 \mu_k, \Lambda_k,Y_k 에 따라 결정되는 상수 행렬

식(10)에 y_k = \Pi (RY_k + t) 를 대입하고 K에 대한 이차부등식을 얻으면 s^T A_k s≤0 의 형태가 되고, 선형 부등식 b^T_k s≤0 은 3D keypoint가 카메라의 앞에 오도록 하기 위해 추가됩니다. proposition 3은 GT keypoint가 F^{\epsilon}(x) 내에 있다고 1-\epsilon만큼 확신할 경우 PURSE의 모든 pose도 GT pose가 가능하다고 그만큼 확신하다는 것을 의미합니다. 이처럼, pose 추정을 실제의 확률적으로 보장된 예측 set으로 보는 것은 이를 단일 pose를 보는 식 (11)과 근본적으로 차이가 있습니다.

RANdom SAmple averaGing (RANSAG)

주어진 pose가 PURSE에 속하는 지 확인하는 것은 부등식을 통해 간단하게 확인할 수 있습니다. 그러나 PURSE는 직접적으로 pose를 제공하지 않으므로, 본 논문에서는 RANSAC과 PnP의 최소 solver인 P3P를 효율적으로 활용할 수 있는 RANSAG라는 샘플링 알고리즘을 제안합니다.

nonconvex하다는 제약으로 인해 직접적으로 PURSE에서 샘플링하는 것은 어렵지만, 공과 타원 형태의 간단한 기하학적 구조로 인해 keypoint 예측 set을 식(10)에서 샘플링 하는 것은 쉽습니다. 따라서 각 반복에서(line 3) RANSAG는 3개의 keypoints를 샘플링하고(line 4-5) P3P를 통해 해를 구한 뒤, PURSE에 있는 pose를 허용합니다.(line 6) RANSAG는 일반적으로 약 100개의 유효한 샘플을 T=1000번의 반복을 통해 반환하게 됩니다. 그러나 S^{\epsilon}이 너무 작거나 비어있는 어려운 상황에서는 0개의 샘플을 얻게될 수도 있습니다. 이러한 경우에는 SANSAG는 PURSE에 속하는 지를 판단하지 않고 K개의 keypoint로 PnP를 풀어 ⌊ T/20 ⌋(default 50) 개의 pose를 샘플링합니다.(line 9~12)

pose set을 구한 뒤, RANSAG는 rotation의 평균(line 14)과 translation의 평균(line 15)을 구하여 평균 pose \bar{s} 를 구합니다. ( \bar{s} 는 PURSE에 포함하는지를 확인하지 않음. )

Worst-case error bounds

평균 pose \bar{s} 와 GT pose (R_{gt},t_{gt}) 사이의 error의 상한을 설정하기 위해 pose-to-PURSE 사이의 거리 제곱을 최대화 합니다.

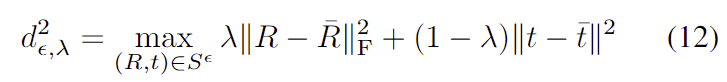
• \lambda ∈[0,1]

특히 \lambda =1 (rotation 거리 최대)와 \lambda =0(translation 거리 최대) 두가지 케이스를 계산하고, proposition 3(GT pose는 S^{\epsilon}에 1-\epsilon확률로 존재한다)에 따라 아래의 식으로 나타나며

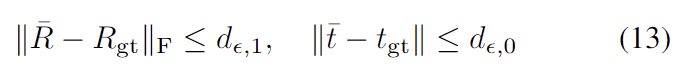
확률은 1-\epsilon 으로 유지됩니다.

Computing the bounds

식(12)는 PURSE S^{\epsilon} 의 제약으로 인해 nonconvex하고, 이를 SDP(semidefinite program)를 이용하여 완화하고 기존에 존재하는 solver를 이용하여 최적화합니다. 이렇게 될 경우 최적의 SDP 값은 식(12)의 최적의 해와 동일할 수도 있고, 정확하지는 않지만 최적의 SDP는 식(12)의 최적값에 대한 상한을 제공할 수 있습니다. 이를 통해 최악의 error를 제한할 수 있습니다.

Experiments

실험파트에서는 LineMOD Occlussion 데이터셋을 이용하여

1. exchangeability 가정 (Theorem 1)을 정당화합니다.
2. 최적의 적용 사례를 제안하기 위해 PURSE의 경험적 적용 범위를 평가하고 Theorem 1의 정확성을 확인합니다.
3. 최악의 오류 범위를 계산하고 tightness와 looseness를 보입니다.
4. 평균 pose 가 다른 방식보다 좋거나 유사한 정확도를 얻을 수 있다는 것을 보입니다.

1. Dataset and Exchangeability

LM-O 데이터는 8개의 object를 촬영한 1214개의 test 이미지가 있으며, 그 중 200개의 이미지는 BOP challenge에서 사용되었습니다. 본 논문의 실험에서는 200개의 이미지를 calibration에 사용하고, 1214개의 이미지를 test에 사용하였습니다. 앞서 Theorem 1에서 이야기하였듯이 exchangeability 가정은 단일 비디오 시퀀스에서 수집되면 문제가 발생합니다. 그러나 LM-O의 원형 데이터인 LM(LineMOD)데이터 셋에 따르면

In order to guarantee a well distributed pose space sampling of the dataset pictures, we uniformly divided the upper hemisphere of the objects into equally distant pieces and took at most one image per piece. As a result, our sequences provide uniformly distributed views…

Stefan Hinterstoisser., et. al, “Model based training, detection and pose estimation of texture-less 3d objects in heavily cluttered scene” ACCV., 2012.

즉, 각 샘플링 위치에서 최대 1장의 사진을 촬영한 것으로, 시간축으로 관련되어있지 않고 1214개의 이미지가 모두 독립적이라는 것을 의미합니다. 따라서 exchangeability를 만족합니다.

2. Empirical coverage

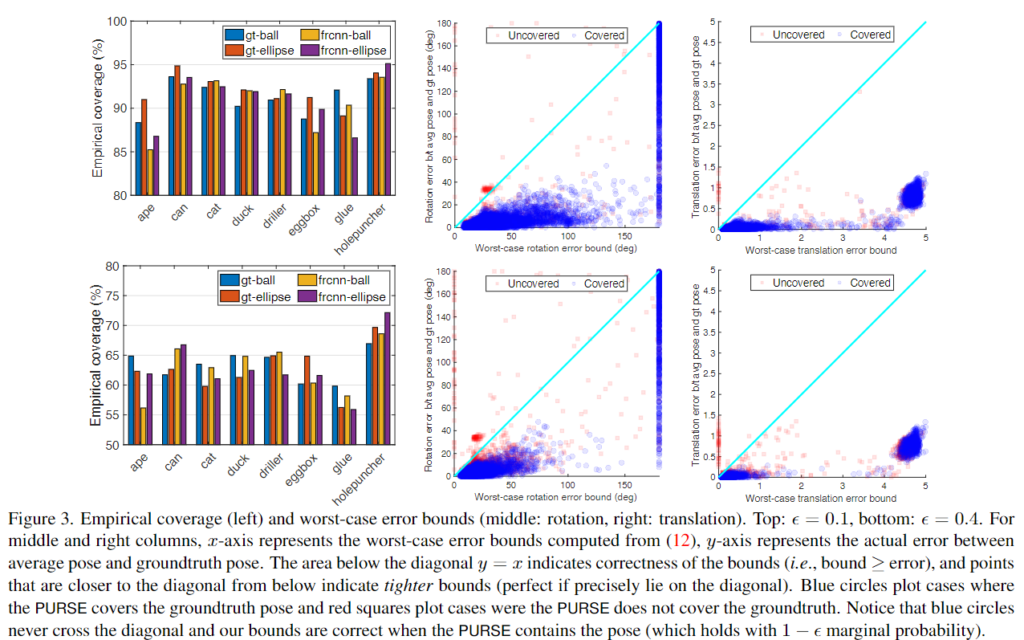
본 논문은 heatmap을 공과 타원 형태로 conformalizes합니다. GT와 Faster RCNN의 bounding boxes에 대해 ball과 ellipse를 적용하여 4가지 변형인 GT box + (ball) & (ellipse)와 Faster RCNN의 box + (ball) & (ellipse)를 Keypoint로 이용합니다. 아래의 Figure 3의 왼쪽 그래프 2개는 \epsilon =0.1(위), \epsilon =0.4(아래)에 대한 empirical coverage를 나타낸 것으로, 8개 object 모두 \epsilon =0.1에서 약 90%, \epsilon =0.4에서 약60% 의 empirical coverage를 가집니다. 셋째로, 대부분의 test 이미지에 대해 타이트한 경계를 가지고 특히 \epsilon=0.4일 때 더 타이트해지는 것을 볼 수 있으나(파란색 점들이 왼쪽 하단부에 모임), keypoint prediction set이 너무 커지면 지나치게 conservative해질 수 있습니다.(파란 점들이 오른쪽 면에 선처렴 경계가 생김) 오른쪽 그래프들을 통해 rotation 뿐만 아니라 translation에서도 유사한 결과를 확인할 수 있습니다.

3. Worst-case error bounds

Figure 3의 중간의 그래프는 worst-case rotation error의 경계(x축)와 실제 rotation error(y축)를 시각화 한 것입니다. 먼저 PURSE가 GT를 커버할 때(파란색 원) rotation error의 범위는 실제 error보다 큰것을 확인할 수 있습니다. 둘째로, error 비율이 증가하면 (아래표) 파란 원들이 x=y 방향으로 이동하는 것을 통해 error 범위가 좁아지는 것을 확인할 수 있습니다.

4. Accuracy of the average pose

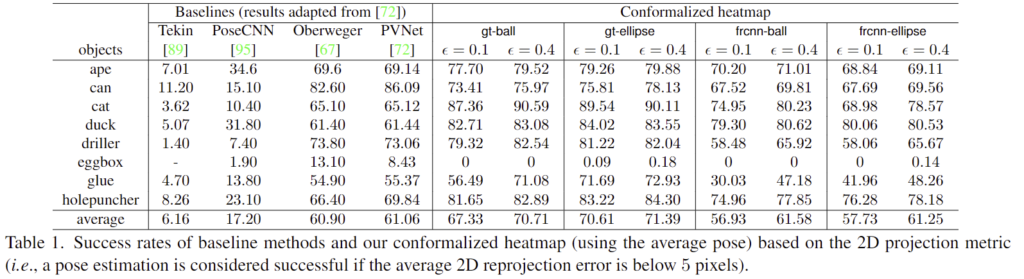
아래의 Table 1은 2D projection을 통해 평균 pose를 구하는 기존 연구들과의 성능을 비교한 것입니다. 5픽셀 이하의 오차일 경우 추정이 정확한 것으로 평가하며, Table 1을 통해 본 논문에서 제안한 평균 poes가 GT를 이용할 경우 더 좋은 성능을 보이고, Faster R-CNN에 이용할 경우에는 유사한 성능을 보이는 것을 확인할 수 있습니다. 또한, \epsilon이 증가함에 따라 평균 pose의 정확도가 더 좋아지는 것을 확인할 수 있습니다.