[CVPR2023] Trap Attention: Monocular Depth Estimation with Manual Traps

이번에 소개드릴 논문은 CVPR2023에 게재된 단안 영상 깊이 추정 방법론입니다. 제가 주로 self-supervised learning 방법론들에 관심이 많아서 리뷰도 그 분야 위주로 보는 편이지만, 이번에 소개드릴 논문은 지도학습 기반 방법론입니다.

Intro

논문의 인트로는 매우 단순합니다. 모델의 정확도는 올리면서 모델의 크기, 속도는 가볍고 빠르게 하자는 것이죠. 제가 최근에 들고 오는 논문들의 성향이 모두 정확도는 유지 혹은 향상시키면서 모델은 가볍고 빠르게 인 것 같은데.. 아무래도 ViT가 나온지 3년이 되면서 정확도는 어느 정도 만족을 했지만 Attention의 연산량에 대해서는 여전히 문제가 되어 개선이 요구되는 것 같습니다.

본 논문에서는 Transformer의 Multi-head Attention(MHA)을 대체할 새로운 기법을 제안합니다. 논문의 제목에서도 볼 수 있듯이 Tran Attention이라고 명칭을 하였는데, 이는 Attention 과정에서 Trap이라는 기법을 활용한다고 합니다. 사실 여기서 이 Trap라고 하는 것이 어떤 의미를 내포하는지는 잘 모르겠지만.. 방법론 자체는 단순해서 과정은 쉽게 이해하실 수 있을 것이라고 생각됩니다.

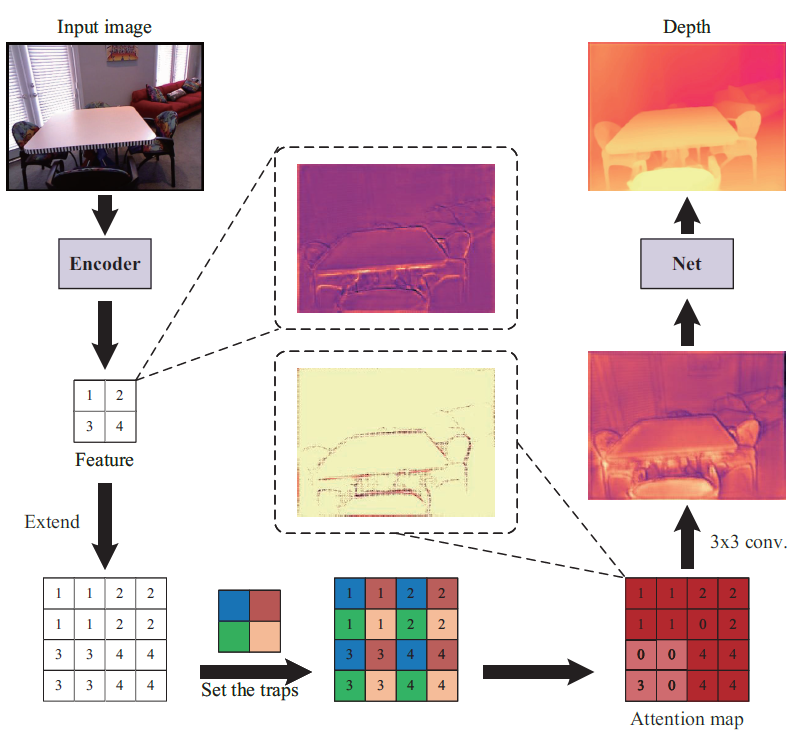
위에 그림 1은 논문의 핵심 컨셉을 대략적으로 표기한 그림인데, Encoder를 타고 나온 feature에 대해서 trap을 설정한 후, 해당 trap에 대해 어떠한 연산을 해서 attention map을 생성하게 됩니다. 이렇게 생성된 attention map을 토대로 다시 컨볼루션 연산을 수행하다보면 Depth map이 나온다 라는 그림인데 사실 해당 teaser 그림만으로는 논문의 핵심을 이해하기가 쉽지가 않습니다.

그러니 바로 본론으로 넘어가서 자세히 알아보시죠.

Method

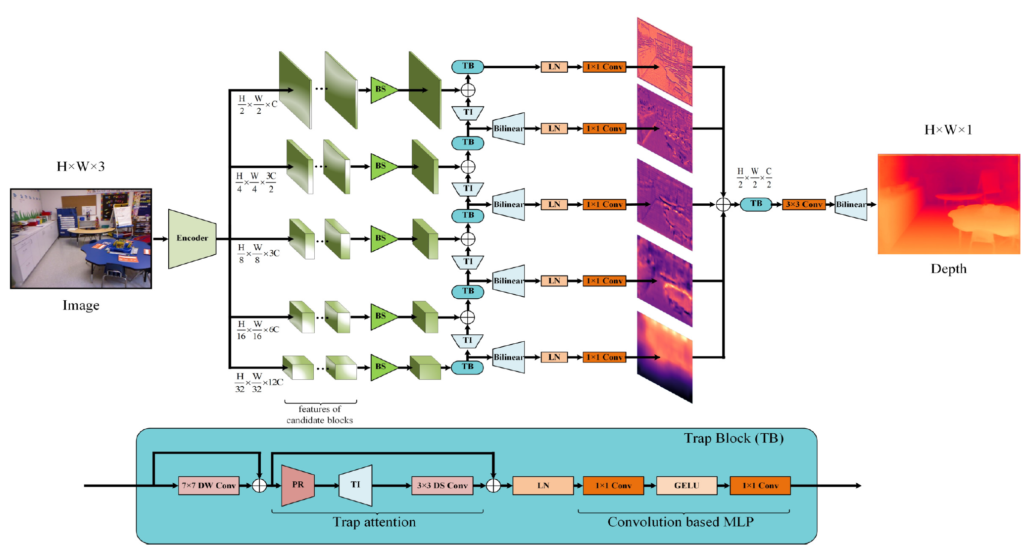
그림2는 논문의 프레임워크를 나타냅니다. 보시면 Encoder를 통해서 1/2 부터 1/32 까지 5가지 스케일에 대한 feature map을 추출하게 되며, low resolution부터 high-resolution까지 디코딩되는 과정에서 저자가 제안하는 Trap Block이 활용이 됩니다.

여기서 Trap Block 내부에는 Trap Attention과 Covonlution 기반의 MLP로 구성된 Feed Forward Network가 있는 것을 확인하실 수 있습니다. 본 논문의 핵심은 Trap Attention을 수행하는 과정이기 때문에 일단 해당 부분에 대해서 자세하게 알아보겠습니다.

Trap Block

먼저 Trap Attention은 Multi-Head Attention을 대체하기 위해 저자가 제안하는 방법론입니다. 보통 Transformer Block의 경우 MHA 연산을 수행 후 FC layer 2개로 이루어진 Feed Forward Network를 거치게 되는데, 저자도 이와 유사하게 Trap Block 안에는 Trap Attention과 Convolution 기반 FFN으로 구성을 한 모습입니다.

한가지 차이점은 맨 처음에 7×7 커널 크기의 Depth-wise Conv 연산을 수행하게 되는데, 이는 기존 MHA 연산의 경우 global level에서 attention을 수행하게 될 경우 영상 전체에 대한 receptive field를 가지게 되는데, 저자도 모델의 receptive field를 넓히는 관점에서 7×7 크기의 (large?) 커널을 활용해 모델의 receptive field를 넓히고자 하였다고 합니다.

7×7 DW conv를 활용하는 것은 이제 많은 백본 논문들이 활용하는 방식이기 때문에, 기존의 트렌드를 따라갔다고 이해하시면 좋을 것 같습니다.

Pixel Rearrangement(PR)

7×7 DW conv를 통과하고 나면 본격적으로 Trap Attention을 수행하게 되는데, Trap Attention의 가장 첫번째 과정으로는 Pixel Rearrangement(PR)이 들어가게 됩니다. PR 연산은 이름은 거창해보이지만 쉽게 말하면 pixel shuffle 연산의 반대되는 연산이라고 이해하시면 될 것 같습니다.

pixel shuffle에 대해서 모르시는 분들이 있을 것 같아 간단하게 소개드리면, Super Resolution task에서 고해상도의 영상을 빠르고 효율적으로 추정하기 위해 channel축의 값을 spatial information으로 변환하는 연산을 종종 사용해왔었습니다. 즉 어떠한 output feature map의 해상도가 \mathcal{R} \in \frac{H}{2} \times \frac{W}{2} \times 4C 라면, pixel shuffle 연산을 수행하게 될 경우 채널축에 있던 값들이 spatial 축으로 이전이 되면서 H x W x C의 값으로 변환이 되는 연산인 것이죠.

이러한 연산을 반대로 한다는 것이기 때문에 기존 feature map이 H x W x C라면 이를 \mathcal{R} \in \frac{H}{2} \times \frac{W}{2} \times 4C 로 변환했구나 라고 이해하시면 될 것 같습니다.

이렇게 down sampling을 해주는 이유는 바로 뒤에서 소개드릴 manual trap이라는 기법이 어찌보면 upsampling하는 과정이기 때문이라고 생각을 해주시면 좋을 것 같은데 이에 대한 내용을 바로 밑에서 소개드리겠습니다.

Manual Traps

feature map에서 유의미한 정보를 추출하기 위해 feature map에 다양한 manual trap 연산을 수행하여 feature map의 종류를 확장시켰다고 합니다. 이러한 확장을 저자는 trap interpolation(TI)라고 명칭을 지었는데, 여기서 manual trap의 종류들은 아래와 같습니다.

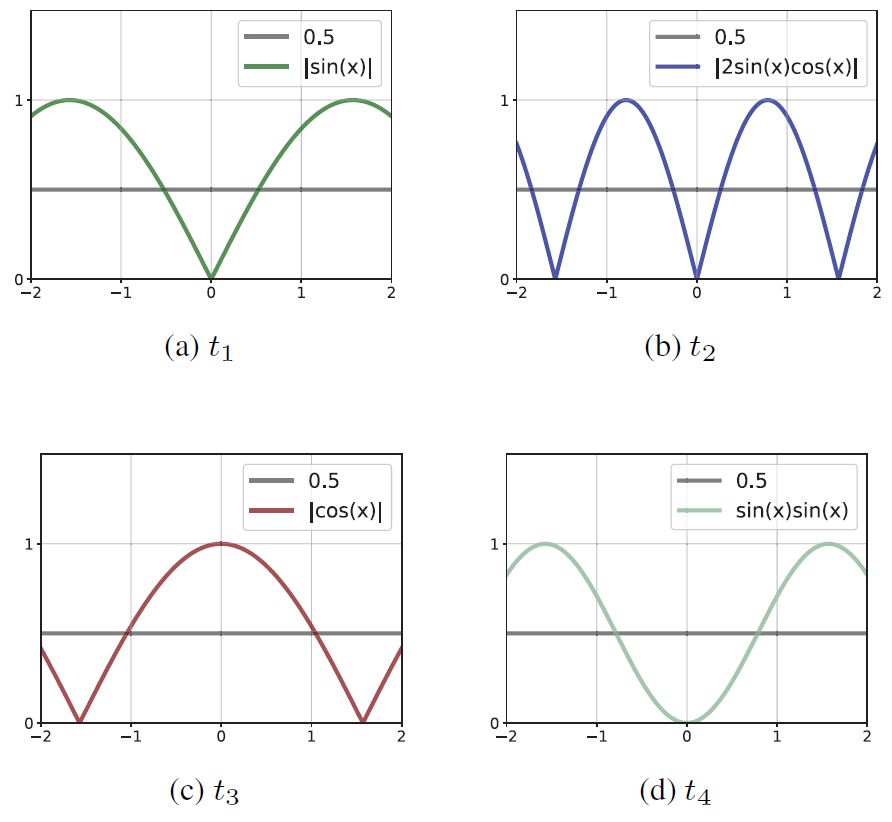
총 4가지의 함수가 존재하며 이들 함수는 sin과 cos등을 적절히 사용하는 것으로 확인하실 수 있습니다. 저자의 주장에 따르면, sin과 sin 제곱의 경우에는 입력 feature map을 보다 더 잘 구분, 보완 혹은 불필요한 영역을 제거하는데 사용될 수 있다고 하며, 그림3의 b의 경우에는 frequency가 더 높기 때문에 더 강하게 구분, 보완, 제거의 역할을 수행한다고 합니다.

그리고 그림3의 c의 경우에는 다른 함수들과 다른 형태의 분포를 바라보기 때문에 a, b, d를 통해서 완전히 제거되는 feature를 적절히 살려주는 역할이라고 합니다. 사실 논문에서는 manual trap의 목적 및 설계 과정에서의 철학등이 나와있지 않고 너무 모호하게 설명하는 감이 없지 않아 있습니다.

본인들이 제안한 것이라면 보다 제대로된 고찰이 있을 것이라고 생각을 했는데, 없어서 당혹스러웠는데 사실 알고 보니 이러한 sin, cos의 조합을 통해서 feature map의 다양한 특징들을 선별해오는 방식이 기존 19년도 논문에 처음 제안되었다고 하네요. 이 논문을 읽기 전에 읽었으면 좋았을테지만, 다음 번 리뷰에서 19년도 논문을 읽고 해당 함수들의 설계의 이유에 대하여 자세히 적어보도록 하겠습니다.

일단 다시 돌아와서, manual trap에 대해 정리를 드리면 manual trap은 그림3과 같은 4가지 activation function을 통해 feature map에 다양한 정보들을 구분, 보완, 제거의 역할을 상호보완적으로 수행하는 것을 의미합니다. 수식적으로 나타내면 다음과 같습니다.

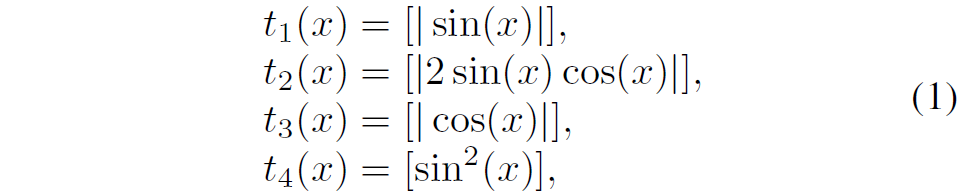
입력 feature map이 x라고 하였을 때 입력 x에 대하여 4개의 함수를 각각 적용해 t1~t4까지의 trap map을 만드는 것이죠. 이렇게 생성된 trap map은 입력 feature map x에 곱해져서 확장된 feature map으로 재구성된다고 합니다.

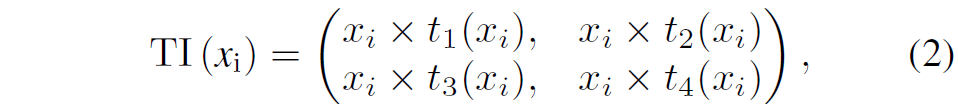
즉 기존의 input feature map x의 i번째 픽셀에 대하여 t1~t4까지 총 4개의 activation map이 곱해진 4개의 값이 존재하게 되는데, 이를 다시 합하는 것이 아니라 이 4개의 값을 그대로 유지한다고 합니다. 즉 x의 feature map이 4개로 늘어나는 것으로도 볼 수 있는데, 저자는 H x W x 4C의 형태로 가지고 가는 것이 아니라 2H x 2W x C의 형태로 해당 값들을 표현하였습니다. 즉 채널 축에다가 쌓는 것이 아닌 spatial dimension에다가 정보들을 저장하는 것이죠.

이러한 방식은 위에서 소개드린 Pixel Rearrangement 과정을 통해 input feature map의 해상도를 1/2로 다운샘플링을 한 이유와 적합하다고 볼 수 있습니다. PR 연산으로 다운샘플링을 시켰다면 그 다음에 TI 연산으로 해상도를 다시 원상시키는 것이죠.

이렇게 TI를 통해서 feature map의 해상도가 H x W x 4C가 되었다면, 저자는 이러한 attention map에 대하여 컨볼루션 연산을 적용함으로써 그들 간에 관계성을 계산하였다고 합니다. 여기서 중요한 점은 뒤에 4C라는 값의 경우 pixel shuffle의 반대되는 PR 연산을 수행하였기 때문에 4개의 채널이 spatial 정보의 의미를 담고 있습니다.

구체적인 예시를 들면 원래 HxW 축에 대하여 pixel 좌표가 [(0,0), (0,1), (0,2), (0,3)…(H,W)]라고 하였을 때 실제 PR연산이 끝난 output의 경우에는 HxW축에 대해 [(0,0), (0,4), (0,8)…] 순으로 정보가 구성이 되어 있습니다. 즉 (0,1), (0,2), (0,3) 위치에 해당하는 정보들은 HxW 축이 아닌 C 채널 축에 담겨져있는 것이죠.

이러한 점을 고려하여 저자는 올바른 spatial information에 대하여 manual trap map들의 관계를 계산하고자 Group Convolution을 활용하였습니다. 쉽게 생각하면 pytorch의 nn.Conv2d에서 모든 c 채널 축에 대해 컨볼루션 연산을 하는 것은 group이 1, Depth-wise conv 연산처럼 각 채널 별로 컨볼루션 연산을 할 때는 group이 C 라고 하였을 때, 4개의 크기로 그룹을 묶어서 컨볼루션 연산하는 group conv는 group 인자를 C//4로 진행해주면 된다는 것이죠.

아무튼 이렇게 group conv까지 적용하여 trap attention을 수행하는 것을 수식으로 표현하면 다음과 같습니다.

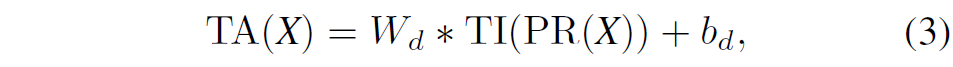
여기서 W_{d}, b_{d} 가 Group Convolution의 가중치와 bias로 \mathcal{R} \in C \times 4 \times 3 \times 3 의 크기를 가지고 있습니다. 즉 3×3 크기의 커널을 가졌으며 4개의 채널을 묶어서 연산하는 컨볼루션이 C개 만큼 있다고 이해하시면 됩니다.

이러한 Trap Attention 방식은 feature map에 대하여 4개의 trap function을 각각 적용해주는 것과, DW, Group convolution 연산만을 진행해주면 되기 때문에 연산량이 입력 해상도에 대하여 제곱배가 아닌 linear하게 증가한다는 것을 확인하실 수 있습니다.

Framework 및 Loss function

이렇게 Trap Attention을 수행하고 나서는 1×1 conv layer와 GELU로 구성된 FFN을 타고 나오면 해당 stage에서의 디코딩 과정이 끝마치게 됩니다. 그 다음엔 그림2에서 보시다시피 적당히 interpolation 해주고, 컨볼루션 연산 해주면서 각 스테이지 별로 Depth map을 생성해주면 되고, 이렇게 생성된 모든 스케일의 Depth map을 fusion해주어서 final depth map을 만든다고 이해해주시면 좋을 것 같습니다.

해당 방법론은 리뷰 처음에서도 소개드렸다시피 지도학습 기반의 방법론이기 때문에 추정된 Depth map과 GT 간에 비교를 함으로써 모델 학습이 수행됩니다.

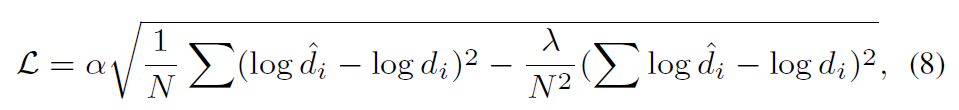
Experiments

그럼 타 방법론들과의 비교 및 ablation study를 보이고 리뷰 마치도록 하겠습니다.

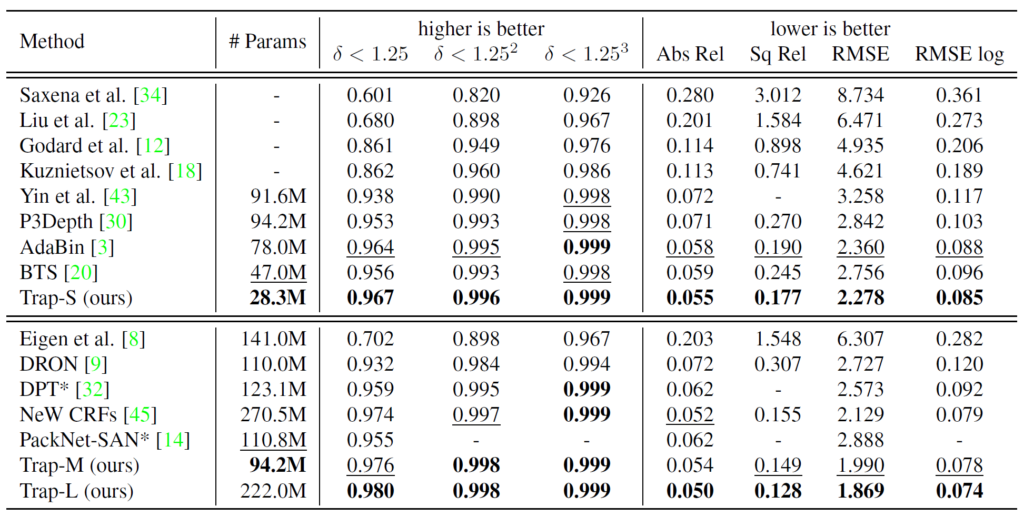
위에 표는 KITTI 데이터 셋에서의 정량적 비교 결과 표 입니다. 모델의 크기는 대략 Trap-S, Trap-M, Trap-L로 구분이 되는데 이는 각각 XCiT-S12, XCiT-M24, Swin-L 모델을 백본으로 활용했다고 합니다.

일단 전반적으로 보았을 때 제안하는 방법론이 모델의 크기 자체는 작으면서도 성능이 타 방법론들 대비 가장 좋을 것을 확인하실 수 있습니다. 여기서 AdaBin, DPT 등과 같은 방법론들은 Transformer의 MHA 연산을 사용하기 때문에 연산량적인 측면에서도 제안하는 방법론이 더 적다라는 것을 추측해볼 수 있습니다.

다만 아쉬운 점은 모델의 크기 뿐만 아니라 추론속도까지 함께 보여주면 좋았을텐데, 해당 부분들을 보여주지 않았다는 점에서 살짝 아쉬움이 있습니다. 아무래도 디코딩 과정에서 연산량이 트랜스포머 기반 방법론들과 비교해서 더 적을 것이라는 생각이 들긴 하지만, manual trip과 같은 연산이 흔하지는 않으니 추론 속도를 가늠하기가 쉽지 않네요.

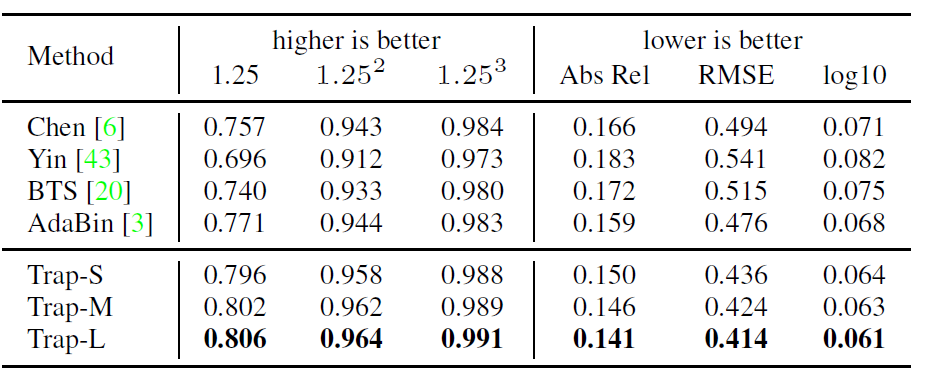
아무튼 제안하는 방법론은 Sun-RGB-D 데이터셋에서도 가장 좋은 성능을 보여주고 있음을 알 수 있습니다. 특히 Sota 논문인 AdaBin과 비교하였을 때 성능 차이가 제법 많이 나는 것이 인상적으로 볼 수 있겠네요. (근데 Adabin 이후의 방법론들 결과는 왜 없지)

Ablation Study

다음은 Ablation study에 대한 결과입니다.

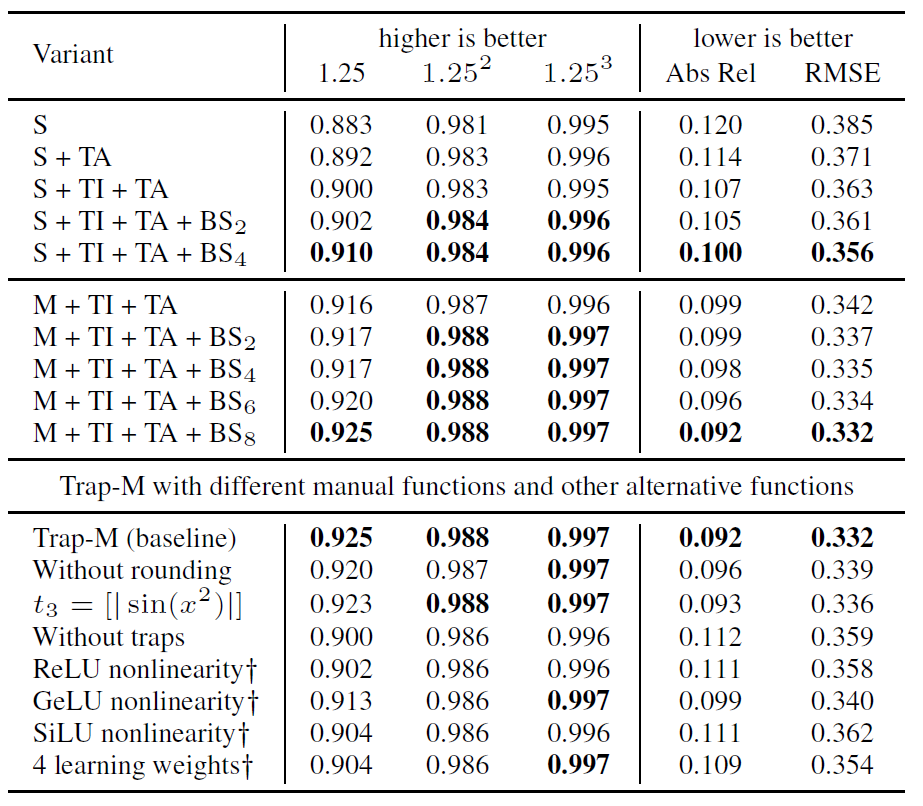
여기서 S와 M은 각각 Trap-S, Trap-M 모델을 의미하는 것이며, BS의 경우에는 인코더 내 i개의 블록들로부터 가장 큰 값을 추출하는 기법이라고 합니다.

먼저 Trap Attention(TA)에 대해서 보시죠. Trap Attention을 적용하게 될 경우 Small model 기준 Abs_rel이 0.120 –> 0.114로 유의미한 향상을 확인하실 수 있습니다.

그리고 2번째 실험으로 TI를 추가하는 경우인데 여기서의 TI는 TA 블록 내부에 TI를 의미하는 것이 아니라, 1/4스케일의 디코더 특징맵이 1/2 스케일로 넘어가는 과정에서 linear interpolation을 사용하는 것이 아니라 TI를 적용하였을 때를 의미합니다.

이 경우에도 0.114에서 0.107로 유의미한 성능 향상이 일어나는 것을 확인하실 수 있습니다.

마지막으로 Block selection이 모델의 정확도를 향상시키는데 매우 중요한 요소 중 하나라고 합니다. 여기서 BS에 대한 설명은 제가 본문에 다루지 않았는데, 컨셉을 간단하게 설명드리면 영상의 배경에 대하여 attention이 제대로 할당되지가 않기에 n개의 반복적인 encoder block의 결과에서 max 값을 뽑아서 사용하겠다는 일종의 stage 내 feature map들을 합쳐서 픽셀별로 maxpooling을 했다고 이해하시면 편할 것 같습니다.

저자는 여기서 전체 block 개수의 1/3 정도 스케일로 후보군을 뽑아서 적용하는 것이 가장 효과적이었다고 주장합니다.

그 다음에도 table4 하단에 Trap-M에 대하여 실행한 다양한 ablation study를 확인하실 수 있는데, 결국 manual trap을 설계할 때 세부적인 디테일들 (반올림을 할 것인지, cos sin 대신 RELU 계열 활성화 함수를 써도 되는지 등등에 대한 실험이므로 관심있으신 분들은 한번 훑어보셔도 좋을 것 같습니다.)

결론

전반적인 pipeline 및 컨셉은 19년도 BTS 논문과 거의 유사하지만, 기존의 방법에 나름의 새로운 설계 및 고찰을 함으로써 모델 크기는 줄이고 큰 성능향상을 달성했기에 CVPR에 게재된 것이 아닐까 싶습니다. 개인적으로 trap function에 대한 컨셉이 재밌긴 하나 조금 더 의미론적인 고찰을 작성해주었으면 좋지 않았을까 합니다.