안녕하세요, 허재연입니다. 한동안 Contrastive Learning을 활용한 Representation Learning 논문을 쭉 읽었었는데요, 결국 해당 방법론들의 설계 핵심 중 큰 부분이 contrastive loss에 있었지만서도 loss에 대한 충분한 분석이 별로 없었던 점과, 제가 SimCLR / MoCo 등 방법론들을 리뷰할 때 항상 temperature parameter (τ)에 대한 질문이 댓글로 달려서 이에 대해 더 잘 이해하고자 Contrastive Loss 관련 논문을 읽어보았습니다.
Representation learning은 unlabeled data를 이용하여 어느정도 데이터의 표현력을 모델에게 사전학습 시키는 작업입니다. 이름 그대로 데이터 자체 특성, 표현을 학습하는 개념입니다. 대표적인 방법으로는 1. 사람이 직접 설계한 handcrafted pretext task를 이용하는 것과 2. contrastive learning을 이용하는 방법이 있습니다. 여기서 contrastive learning은 서로 같은(원본 이미지에서 서로 다르게 augmented 되었거나 label이 동일한 데이터라는 뜻) positive pair끼리는 가깝게, 서로 다른 negative pair끼리는 서로 멀게 임베딩 하는 방향으로 학습을 반복하는 것입니다. 여기서 사용되는 것이 contrastive loss입니다. contrastive loss에 대해서는 이전 세미나에서 소개해 드렸는데요, 이번 리뷰에서 다시 살펴보도록 하겠습니다.

Abstract
저자는 Unsupervised contrastive learning이 상당한 성과를 내는 와중에도 이에 대한 연구가 별로 이루어지지 않았다며 논문을 시작합니다. 해당 논문에서는 unsupervised contrastive learning loss의 동작 과정을 이해하는데 집중합니다. contrastive loss가 hardness-aware loss function임과, temperature parameter τ가 hard negative samples의 penalty 정도를 조정한다는 것을 보여줍니다. 여기서 hard negative sample이란 Anchor와 다른 label을 가지지만 유사한 특징을 가진 sample을 말합니다. hard negative를 잘 구별한다는 것은 특징이 유사하지만 label이 다른 데이터를 잘 구분할 능력을 갖추게 된다는 뜻입니다(하지만 반대로 비슷한 데이터를 다른 label로 라벨링 해버릴 것이니 유사한 데이터를 같은 label로 묶을 수 있는 능력은 떨어지겠죠. trade-off 관계에 있으니 이를 고려하며 loss를 설계해야 합니다). 또한, uniformity와 temperature parameter τ간의 관계를 밝히며, contrastive learning이 separable feature를 학습하는데 uniformity가 중요하다고 말합니다. τ값이 작아지면서 uniformity가 증가하는데, 그럼 τ값이 작을수록 → uniformity의 증가 → separable feature 학습에 유리함 이라는 흐름으로 받아들이시면 될 것 같습니다. 하지만 uniformity를 과도하게 추구하다 보면 의미론적으로 유사한 sample들을 잘 인식할 수 없게 되어 (내제되어있는 의미론적 구조가 깨져버리기 때문에) downstream task에서 잘 동작하지 못하게 된다고 합니다.
이는 instance discrimination의 본질적인 결함으로 볼 수 있다고 합니다. instance discrimination objective는 (sample들 간 내제되어있는 관계를 무시하고)서로 다른 모든 instance는 멀리 밀어버립니다. 의미론적으로 일관적인 샘플들을 서로 분리하는 것은 일반적인 downstream task에 사용할 정보를 얻는데 긍정적인 영향을 미치지 않는다고 합니다. 따라서 잘 설계된 contrastive loss는 의미론적으로 유사한 샘플들 간 어느 정도 허용 범위를 가져야 한다고 합니다. 저자들은 여기서 contrastive loss가 uniformity-tolerance dilema를 충족하며, temperature parameter를 잘 선택하면 분리 가능한 특징을 학습하고 의미론적으로 유사한 샘플들에 대해 어느정도 허용하여 feature의 품질과 downstream 성능을 향상시킬 수 있다는 것을 발견했다고 주장합니다.
Introduction
심층 신경망 기술은 ImageNet, Places과 같은 대규모 human-annotated 데이터셋 덕분에 극적인 발전을 이루었습니다. 이는 수동 labeling에 크게 의존하는데, labeling은 시간과 비용이 너무 많이 드는 문제가 있습니다. 이러한 배경 하에, Unsupervised learning은 사람의 supervision 없이 표현력을 학습할 가능성을 제시합니다. 최근에, contrastive loss를 기반으로 한 unsupervised learning 방법들이 좋은 성과를 내고 있습니다. 대조 학습(contrastive learning)은 raw pixel을 hypersphere space의 feature로 매핑하는 general feature function을 학습하는것을 목표로 합니다. contrastive learning 방법은 positivie pairs끼리는 끌어당기고 negative pairs끼리는 밀어내는 방법으로 동일 instance의 different views(augmentation 등으로 변화를 준 동일 이미지 정도로 생각하면 됩니다)에 불변하는 표현력을 학습하려 합니다. CNN의 강력한 추상화 능력과 강력한 augmentation을 통해 unsupervised contrastive model들은 semantic structure의 일부를 학습 할 수 있습니다. 예를 들어 , Fig1에서 좋은 contrastive learning 모델은 1(a)과 1(b)의 loss가 동일하지만 1(b)의 상황 대신 1(a)과 같은 embedding distribution을 생성하는 경향이 있습니다(loss가 동일하지만 의미론적으로 더 일관성 있는 임베딩 분포를 생성하려 하겠죠)
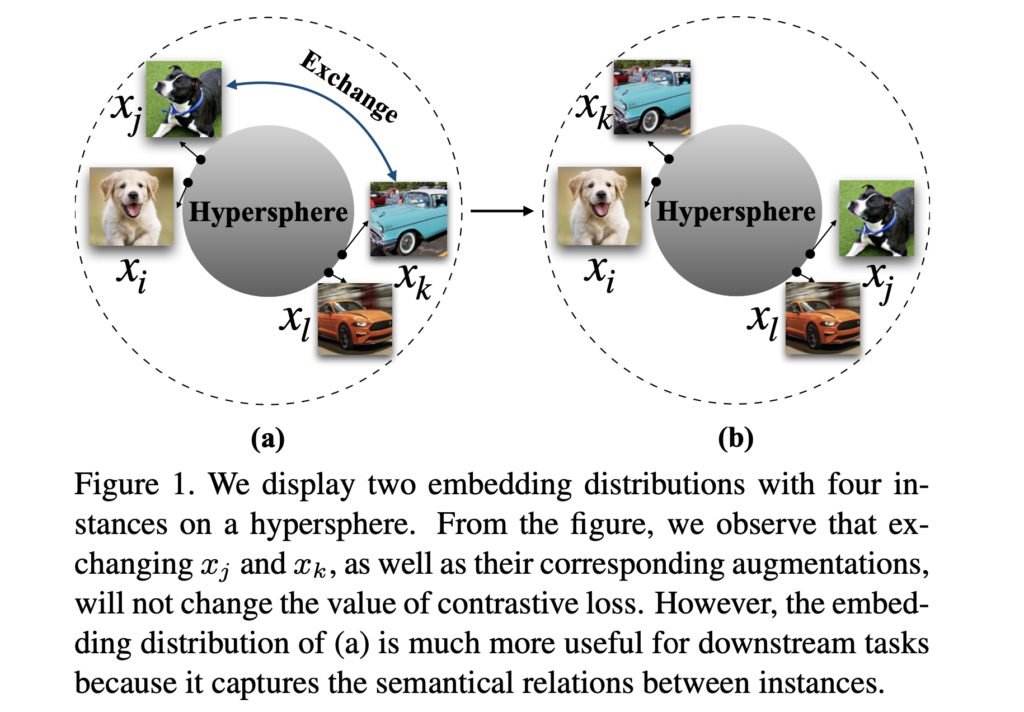
contrastive learning 방법들은 feature유사도의 softmax함수인 loss함수를 활용하는 일관된 구조를 가집니다. 이 때 contrastive loss에 있는 temperature parameter τ는 positive pair와 negative pair를 구분하는것을 도와줍니다. unsupervised contrastive learning에 있어 contrastive loss의 동작이 결정적이므로 , 본 논문에서는 temperature parameter를 이용하여 contrastive loss의 특성을 알아보았다고 합니다. 저자들은 contrastive loss가 자동으로 hard negative sample들을 최적화하는데 집중하는 hardness-aware 손실함수이며, hardness에 따라 이에 penalty를 부여한다는 것을 알아냈습니다. Temperature parameter는 hard negative sample들에 대해 패널티 강도를 조절하는 역할을 합니다. 작은 τ값을 가지는 contrastive loss는 hard negative sample들에 있어 더 penalty를 가하기에 각 샘플의 국소적(local) 구조가 더 잘 분리되며, 임베딩 분포가 더 균일(uniform)해지는 경향이 있습니다. 반면 큰 τ값을 가진 contrastive loss는 hard negative sample들에 대해 덜 민감해지며, τ값이 +∞에 근접해질수록 hardness-aware특성이 사라집니다. hardness-aware특성은 softmax기반 contrastive loss의 성공에 결정적이며, hard negative sampling 전략으로 간단한 형태의 contrastive loss가 좋은 downstream performance를 달성하게 됐다고 합니다.
unsupervised contrastive learning에서 임베딩 분포의 uniformity는 separable feature를 학습하는데 있어 중요합니다. 저자들은 temperature parameter와 임베딩 분포의 관계에 집중했습니다. temperature를 이용해서, uniformity가 contrastive model 성능의 중요한 지표이며, 과도한 uniformity가 의미론적인 구조를 파괴할 수 있다는것을 발견했다고 합니다. 이것은 contrastive objective의 내제적 결함에 의한 것입니다. 대부분의 contrastive learning은 positive pair간의 유사도를 높이고 negative pair간의 유사도를 낮추는 방법으로 instance discrimination task를 학습합니다. 이런 방법으로는 사실 의미론적 관계를 정보를 담고있지 않다고 합니다. 의미론적으로 일관적인 샘플들을 멀리 밀어내는것은 유용한 feature를 만드는데 좋지 않습니다. 만약 contrastive loss가 너무 작다면 loss함수는 (anchor sample과 의미론적으로 유사한 특성을 갖는)이웃 샘플들에게 매우 큰 penalty를 부여 할 것입니다.
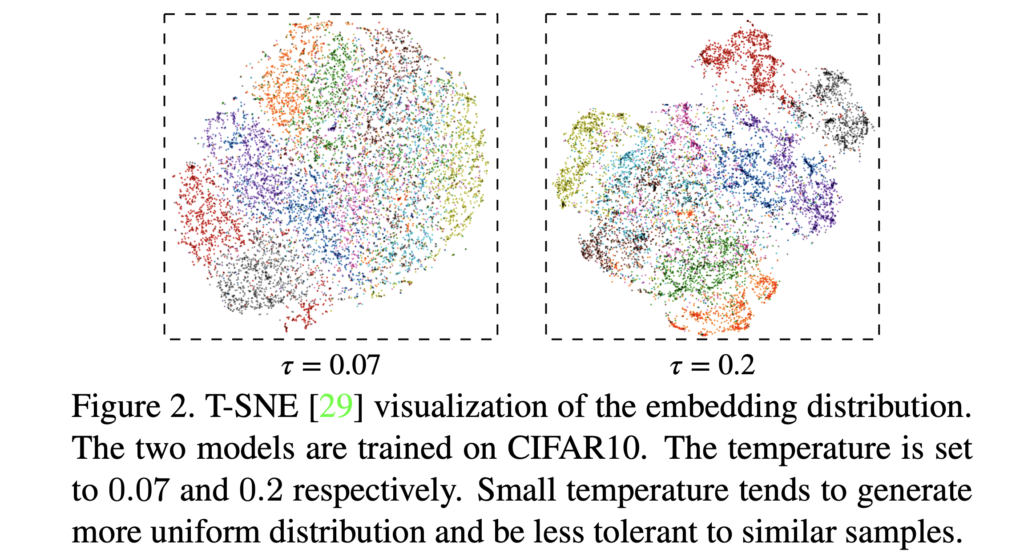
위 Fig2에서, τ=0.07로 훈련되었을때의 임베딩은 데이터가 비교적 균질하게 분포되어있지만, τ=0.2로 훈련된 임베딩은 global로 봤을때는 sparse하지만 유사한 샘플들끼리는 모여있는, 더 의미있는 분포를 보입니다. 작은 τ가 인접한 negative sample들을 서로 많이 밀어냈기에 이런 분포가 생겼다고 생각하시면 됩니다. 저자들은 여기서 unsupervised contrastive learning에 uniformity-tolerance dilemma가 있다고 합니다. 우리는 hard negative sample들이 잘 구별되는 적당량의 uniformity를 원하면서도, 동시에 의미론적으로 유사한 샘플들간의 관계성/일관성 구조가 깨지는것은 원하지 않습니다. 결국 좋은 contrastive loss는 이 두 특성을 적절히 만족해야 합니다. temperature parameter τ는 너무 크지도, 작지도 않게 잘 조정되어야 하겠죠.
저자들은 본 논문을 통한 contribution을 다음과 같이 요약합니다:
- 본 논문에서는 contrastive loss의 동작을 분석해서 contrastive loss가 hardness-aware loss입을 보입니다. 그리고 hardness-aware property가 contrastive loss의 좋은 성능에 크게 기여했다는것을 밝힙니다
- 그래디언트 분석을 통해, temperature가 hard negative sample들에 대한 penalty 강도를 조절하는 주요 파라미터임을 보입니다. 양적/질적 실험을 통해 이를 뒷받침합니다.
- contrastive learning에서는 uniformity-tolerance dilemma가 있으며, temperature를 잘 조정해야 두 특성(uniformity, tolerance)을 잘 활용할 수 있으며 feature quality를 높일 수 있음을 보입니다.
Hardness-aware Property
unlabeled 학습 데이터셋 X = {x1, …, xN}에 대해, contrastive loss는 다음과 같이 표현할 수 있습니다. si,j = f(xi)’ g(xj). 이며, f(·)는 image를 pixel에서 hypershpere space로 매핑하는 feature extractor이고 g(·)는 f(·)와 같거나 memory bank, momentum queue를 거친 feature extractor입니다(서로 다른 데이터 증강을 통해 positive pair를 만드는 신경망이라고 보시면 됩니다).
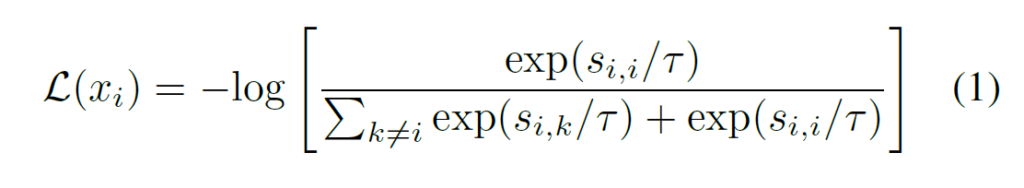
xi가 xj로 인식될 확률은 다음과 같이 나타낼 수 있습니다.
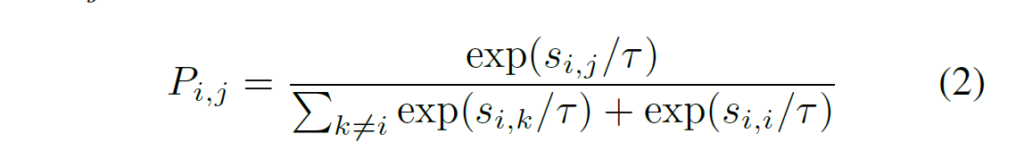
앞에서 몇 번 말씀드렸지만, contrastive loss는 positive pairs끼리는 가깝게, negative sample은 분리되도록 합니다. 이는 다음과 같은 간단한 contrastive loss로도 구현할 수 있습니다. positive 유사도에 -1을 곱해서 유사도가 높을수록 작게, negative pair의 유사도가 크면 loss가 커지게 설계되었습니다
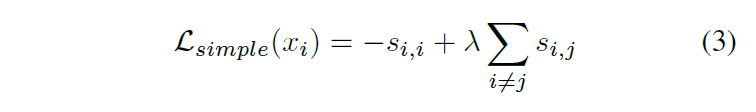
하지만, 위 (3)번 L_simple contrastive loss는 softmax기반 contrastive loss보다 성능이 훨씬 떨어진다고 합니다. L_simple과는 다르게 softmax기반 손실함수는 자동으로 informative negative sample들을 분리하는데 집중해서 임베딩 분포가 더 균일해지게(hard negative sample들끼리 멀어지게) 하는 hardness-aware 손실함수라고 합니다. L_simple은 temperaturen τ가 +∞인 특이 케이스와 동일하다고 합니다. 이 내용은 바로 뒤에 나옵니다.
Gradients Analysis
여기서는 positive sample과 negative sample에 대한 gradient를 분석하였습니다. 결론적으로, positive gradient의 크기는 negative gradient의 합과 같습니다. temperature는 negative gradient의 분포를 조절합니다. temperature가 작을수록 anchor point의 최근접 이웃에 집중하게 되는데, 이는 hardness-aware 민감도를 조절합니다. positive similarity si,i와 negative similarity si,j의 그래디언트는 다음과 같이 표기할 수 있습니다:
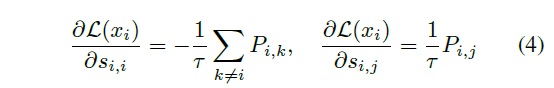
(4)번 수식을 살펴보면 negative sample에 대한 gradient는 exp(si,j/τ)에 비례하며, 이는 contrastive loss가 hardness-aware 손실함수이며, (3)번 L_simple의 모든 negative 유사도에 같은 크기의 그래디언트를 주는 것과는 다른 것을 확인할 수 있습니다. 또한 positive sample에 대한 gradient크기는 각각 모든 negative sample들의 gradient의 합과 같습니다(이를 이용해 temperature의 동작을 이해하는 확률분포를 만들 수 있다고 합니다)
The Role of temperature
위의 식에서 봤듯 temperature는 hard negative sample에 대한 penalty(가까운 샘플을 얼마나 밀어내는지) 강도를 조절할 수 있습니다.
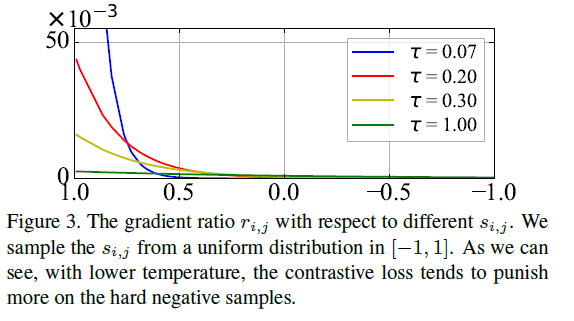
Fig3은 gradient ratio r_i,j( negative sample gradient / positive sample gradient ), 샘플 간 유사도, temperature간의 관계를 보여주고 있습니다. ri 분포 similarity가 높을수록(1.0에 가까울수록) 가파른 것을 못 수 있는데, 이는 xi(anchor)에 가까울수록 큰 penalty(밀어내는 효과)를 주는 것으로 해석할 수 있습니다. 특히 temperature값이 작을수록 이 현상이 심해지고(가까운 샘플들을 밀어내는 경향이 쎄지기 때문에 uniform distribution을 띄게 되고), temperature값이 커지면 유사도가 크던 작던 별 영향을(penalty)를 주지 않습니다. 급격히 작은 temperature는 최근접 이웃 한두개 샘플에 극단적으로 집중하게 됩니다. 한 번 temperature값을 극단적으로 크게/작게 근사시켜 보겠습니다.
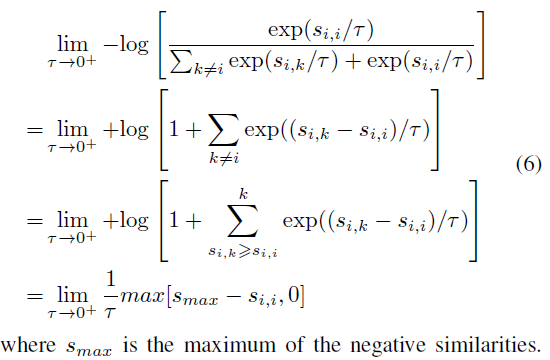
temperature값을 0에 근사시키면 contrastive loss가 margin값이 0인 triplet loss와 같아지는데, 이는 최근접 negative sample들에 집중하게 된다고 합니다.(triplet loss에 대해서는 아직 제가 잘 알지 못해 깊게 이해하지 못했습니다). (6)번 손실함수를 이용하면 모델은 유용한 정보를 전혀 학습할 수 없다고 합니다.(유사한 샘플끼리의 관계를 전부 깨버리니 의미있는 정보를 활용할 수 없을 것입니다)
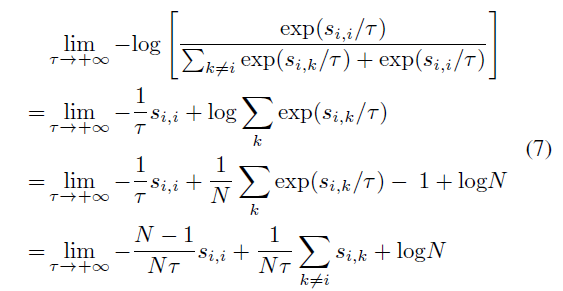
temperature값을 무한대로 발산시킬 때 수식입니다. 중간중간 테일러 근사를 통해 식을 간략하게 표기했습니다. 이 수식을 보면 근사시킨 contrastive loss가 위에서 보았던 L_simple과 같다고 합니다(L_simple은 negative sample간 gradient값의 차이가 없었죠). 이 손실함수를 이용하면 적절하게 조정된 temperature를 사용한것보다 성능이 좋지 못하다고 합니다.
Uniformity-Tolerance Dilemma
임베딩 분포의 균일성(uniformity)와 유사 샘플에 대한 오차 허용(tolerance)은 모두 feature 품질에 중요한 특성입니다. 하지만 앞에서 계속 얘기했듯 이 둘은 temperature를 조정함에 따라 trade-off 관계에 있습니다. 이 부분에서 설명이 많긴 한데.. 다음 표를 바로 보시는게 이해가 빠를 것 같습니다.
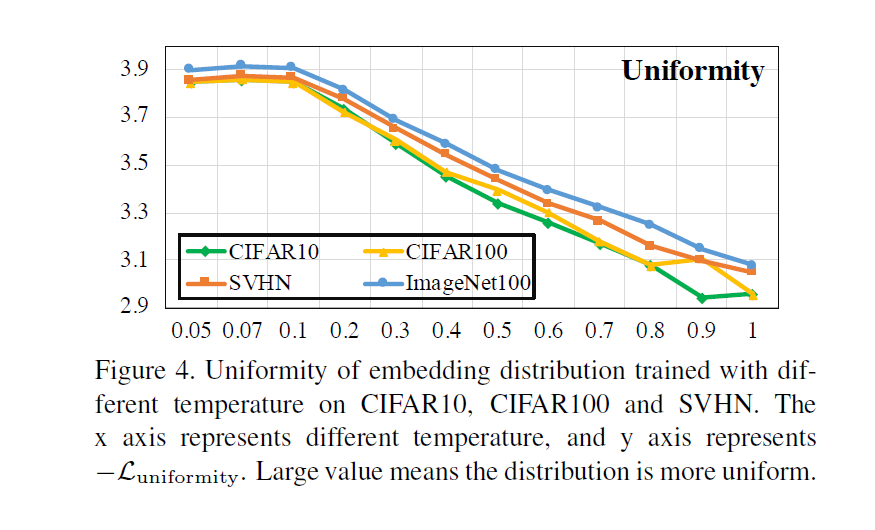
임베딩 분포의 uniformity를 정리한 표입니다. 각각 다른 데이터셋에 대해, 다른 temperature가 적용되었습니다. 세로축이 uniformity이고 가로축이 temperature이니, temperature가 작아질수록 uniformity가 커지는 분포를 일반적으로 따르더라.. 라고 요약 할 수 있습니다. uniformity에 대해 보았으니 tolerance에 대해서도 보겠습니다.
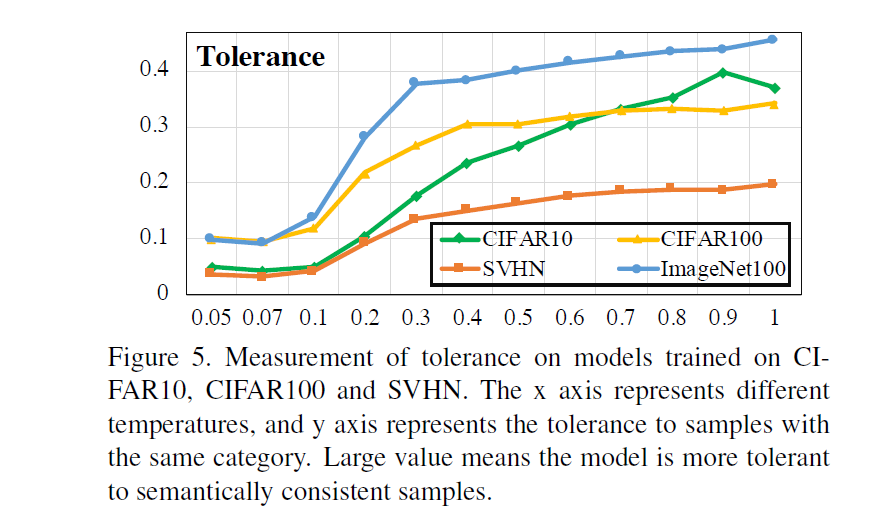
uniformity와 는 반대 경향을 보입니다. temperature값이 커질수록 tolerance가 비례해서 증가하는 것을 확인할 수 있습니다. 이는 결국 유사한 샘플들끼리 cluster되게 유지하기 때문에 의미론적 구조가 잘 보존되는 임베딩 공간을 만들 수 있습니다(하지만 너무 큰 temperature값을 쓴다면 위에서 말했다시피 제대로 학습이 되지 않을 것입니다)
저자들은 temperature값을 키우거나 줄임으로서 uniformity와 tolerance가 너무 커지거나 작아지게 하지 않고 싶어했습니다. 딜레마에 대해 더 안정적인 loss를 찾고 싶어했죠. 이에 따라 hard contrastive loss에 대한 결과도 보였습니다.
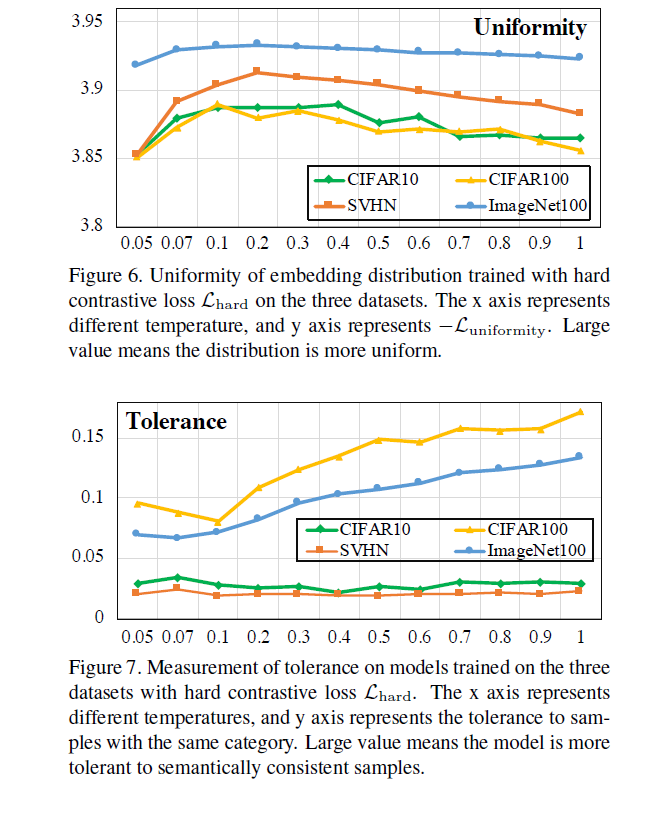
hard contrastive loss는 uniformity-tolerance dilemma를 더 잘 다룰 수 있습니다. 일반적인 손실함수보다 uniformity가 비교적 안정적임을 확인할 수 있습니다.
Experiments
여기에서는 temperature값에 대한 다양한 실험을 보였습니다.
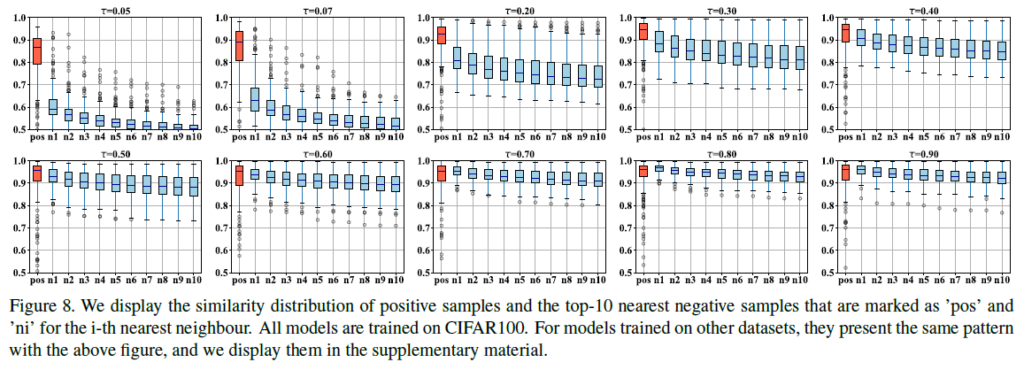
위 표에서는 positive sample과 top-10 nearest negative sample들에 대한 유사도 분포를 보입니다. 데이터셋은 CIFAR100을 사용했지만, 다른 데이터셋을 사용한 실험에서도 이와 일관적인 결과를 보였다고 합니다.
결과를 살펴보면 τ값이 작아집에 따라 positive sample과 다른 confusing negative sample들간의 차이가 커집니다(hard negative sample들을 잘 분리해냈지만, 임베딩 구조의 일관성이 약해지겠죠). τ가 증가하면 반대의 경향을 보입니다(그리고 positive similarity가 1에 가까워집니다). confusing negative sample들을 구별하는 능력은 떨어지게 됩니다.
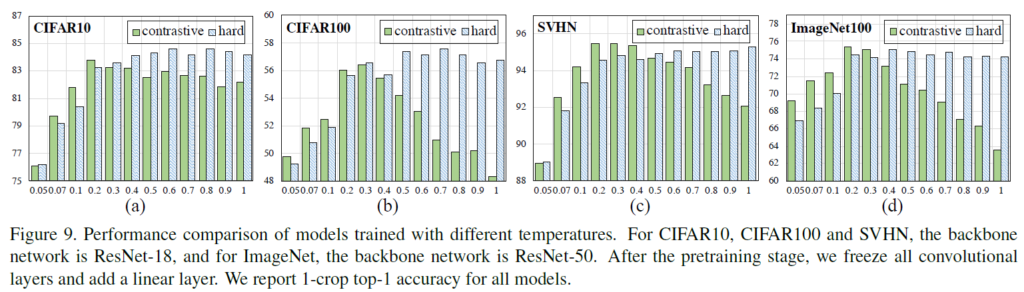
hard contrastive loss에 대한 실험도 있습니다. 실험을 보면 hard contrastive loss를 사용했을 때 uniformity-tolerance dilemma가 완화됩니다. 일반적인 contrastive loss는 temperature 값에 따라 무지게 모양을 그려서 적절한 값을 찾는것이 매우 중요하지만(uniformity-tolerance dilemma), hard contrastive loss는 이에 대해 좀 더 유연한 것을 확인할 수 있습니다.
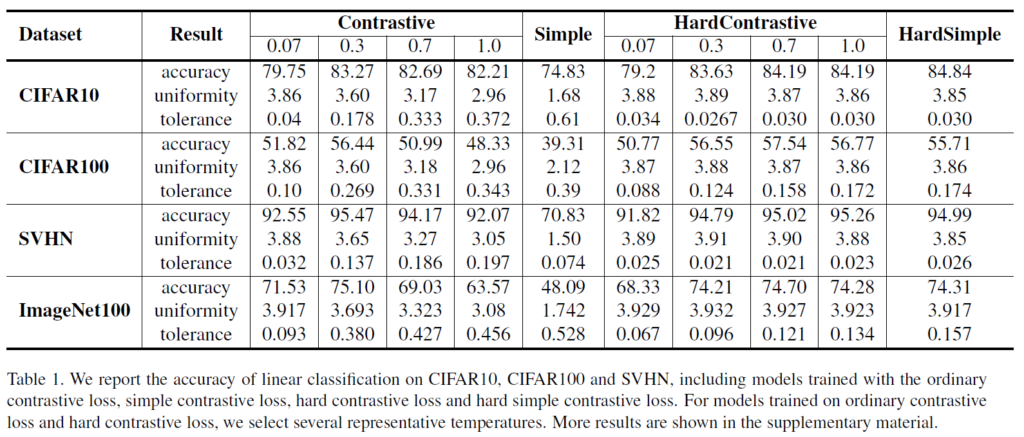
앞서 언급한 다양한 요소들을 종합한 표입니다. simple loss인지, softmax 기반 loss인지, hard contrastive loss인지에 따라 정리되어 있으며, temperature값에 따른 uniformity, tolerance값과(이 둘은 trade-off관계에 있는것을 확인할 수 있습니다) 전반적 성능이 나와있습니다.
Conclusion
본 논문에서는 unsupervised contrastive loss의 동작에 대해 면밀히 탐구했습니다. 지금까지 contrastive learning을 이용한 visual representation learning 논문을 읽으면서 loss의 동작에 대한 자세한 분석이 나와있지 않아 답답했었는데, 이를 읽으면서 어느 정도 해소된 것 같아 만족스럽습니다. 결국 contrastive loss가 hardness-aware 손실함수이며, 이 특성이(hard negative sampling 과정을 거치며) contrastive loss가 좋은 성능을 내는데 중요하다는것을 보였습니다. 또한 temperature parameter τ가 임베딩 분포의 local separation과 global uniformity를 결정하는데 핵심적으로 작용한다는 것을 확인할 수 있습니다. 이 τ를 이용해 contrastive learning의 한계점인 uniformity-tolerance dilemma에 대해 살펴보았습니다. 저자들은 이 딜레마가 다른 인스턴스간의 관계를 명시적으로 모델링 함으로써 해결 될 수 있을 것 같다고 합니다. 본 논문이 이후 연구자들이 딜레마를 해소하는데 도움이 되길 바란다며 논문이 마무리됩니다.
안녕하세요. 허재연 연구원님.
좋은 리뷰 감사합니다. 덕분에 temperature 파라미터가 정확히 어떤 식으로 작용하는지 한층 더 잘 이해하게 된 것 같습니다.
리뷰를 잘 작성해주셔서 본 논문에 대해서는 잘 이해가 되었는데요, 하나 궁굼한 것이 저자들이 마지막에 t 값에 따라 uniformity-tolerance 딜레마가 발생하는 것을 개선하기 위하여 인스턴스 간의 관계를 모델링 한다고 하였는데, 혹시 이 논문 이후로 이러한 연구가 더 진행되었을까요?
감사합니다.
백지오 연구원님, 댓글 감사합니다. 저도 후속 연구가 있나 궁금해서 인용 논문과 1저자의 최신 논문 리스트를 쭉 훑어봤는데 .. 결론적으로 의미있는 후속 논문은 찾지 못했습니다. 그럴듯한 논문들도 contrastive loss의 trade-off나 인접 instance간의 모델링에 집중한 논문은 아니었습니다.
아직 학회/저널에 accepted된 논문이 아니어서 추천드리기 조심스럽긴 한데, 관심 있으시다면 다음 논문을 한번 훑어보시는것을 추천드립니다 : https://arxiv.org/abs/2301.11673
리뷰한 논문과 focus가 fit한 논문은 아니지만, 함께 읽으면 의미 있을 것 같아 보입니다.
안녕하세요. 좋은 리뷰 감사합니다.
리뷰를 꼼꼼하게 해주셔서 잘 모르는 분야이지만 덕분에 쉽게 이해할 수 있었습니다. 간단한 질문이 있는데요. temperature를 이용해서, uniformity가 contrastive model 성능의 중요한 지표이며, 과도한 uniformity가 의미론적인 구조를 파괴할 수 있다는것을 발견했다고 말씀하셨는데, 의미론적 구조에 대해서 뭔가 잘 와닿지 않아서 그런데 혹시 설명 부탁드려도 될까요?
감사합니다
음, 결국 저희가 contrastive learning을 무엇을 위해서 수행하는지를 염두하며 생각하시면 이해가 수월할 것입니다. 저희는 unlabeled data로 contrastive learning을 수행함으로 결국 사전학습의 대상이 되는 모델이 데이터 자체에 대한 이해력/표현력을 최대한 확보하길 원합니다. 결국 의미론적으로 유사한 sample들에 대해서는 일관성을 가지면서도, 의미론적으로 거리가 먼(예를 틀자면 classification에서는 다른 class인)데이터끼리는 확실한 구분을 원합니다. uniformity는 hard negative pair에 대한 분별력을 갖출 수 있지만, 과도한 uniformity를 추구하다 보면, 바꿔 말해 nearest neighgbors끼리의 discrimination을 과도하게 추구하다 보면 유사한 데이터들간의 관계가 유지되지 못하게 됩니다. 우리는 유사한 특성을 가진 sample들끼리는 임베딩 공간에서 clustering되어있길 원합니다(유사한 데이터에 대해서는 일관성을 가지고, 유사하지 않은 데이터에 대해서는 확실하게 분별하는것이 저희가 contrastive learning에 기대하는 것이기 때문이죠). 의미론적인 구조를 파괴한다는 것은, 비슷하게 clustering되어있어야 하는 데이터끼리의 관계마저 끊어버리게 된다는 뜻입니다. Fig2를 참고하면 이해가 쉬울 것이라 생각됩니다.
안녕하세요. 좋은 리뷰 감사합니다 ! !
si,j = f(xi)’g(xj)여기서 f(xi)’는 무엇인가요 ? f(.)는 이미지를 pixel에서 hypershpere space로 매핑하는 feature extractor라고 하셨는데 f(.)’는 무엇인지 궁금합니다.
또, xi가 xj로 인식될 확률인 P_i,j는 갑자기 왜 나온 것인가요 ? 주위에 있는 식인 2, 3에도 포함되어 있지 않은데 혹시 gradients analysis 부분에서 positive similarity si,j와 negative similarity si,j의 그래디언트를 표기할 때 사용되는 것인지 궁금합니다 . 여기 gradient를 분석한 결과로 positive gradient의 크기는 negative gradient의 합과 같다고 했는데 좀 더 자세히 설명해주실 수 있으실까요 ? 그냥 분석 결과가 그렇게 나온것인가요 ?
마지막으로 simple contrastive loss 같은 경우에는 간단하지만 softmax 기반 로스보다 성능이 더 떨어지는데 이 simple loss가 사용되는 이유가 있나요 ? 아니면 이 simple loss가 먼저 등장하였고 이의 단점을 보완하고자 이후에 softmax 기반 loss가 등장하게 된 것인지 궁금합니다.
감사합니다 !
정윤서 연구원님, 좋은 질문 감사드립니다. 질문이 많은데, 하나씩 답변드리겠습니다.
xi는 input image data, f()는 신경망을 의미하니 이미지가 신경망을 통과한 ouput인 f(xi)는 신경망의 출력인 representation vector를 의미합니다. contrastive loss를 구성할 때 두 representation 간의 유사도 매트릭스를 만드므로, si,j = f(xi)’g(xj)는 두 벡터의 곱으로 생성한 행렬로 받아들이시면 됩니다. 여기서 f(xi)’는 f(xi) 벡터를 transpose시킨 것을 의미합니다. 벡터 곱을 위해 전치시킨 것입니다(논문의 표기를 따랐습니다).
정윤서 연구원님이 말씀하신 것처럼 P_i,j는 식 (4)에서 다시 등장합니다. 저는 표기를 간단하게 함과 동시에 P_i,j 자체만으로도 의미가 있으니 따로 표기했다고 받아들였습니다
positive gradient와 negative gradient의 결과는 그냥 수학적으로 (1)번 수식인 contrasitve loss 를 편미분한 결과입니다. 먼저 수식적으로 보이고 그 결과를 가지고 동작을 해석한 것이라 받아들이시면 되겠습니다.
simple loss는 저도 이 논문에서 처음 본 것이고, 적어도 제가 지금까지 본 contrastive learning 논문에서는 전혀 본 적이 없습니다. 그냥 positive 유사도를 높이고 negative 유사도를 낮추는 기능만 생각하면 이렇게 간단하게 loss를 구성할 수도 있다, 그리고 temperature를 무한대로 보낸 것과 같은 기능을 한다 정도로 생각하시면 될 것 같습니다(temperature를 발산시킨 근사함수를 먼저 만들어 놓고 역으로 simple loss를 만든게 아닐까 개인적으로 생각합니다). contrastive loss는 제가 알기로는 처음 제안될 때부터 softmax기반으로 제안된 것으로 알고 있습니다.
좋은 질문 감사합니다.