[ICML 2023] Towards Controlled Data Augmentations for Active Learning

이번에 리뷰할 논문은 Active Learning 에 Augmentation을 접목시킨 논문입니다.

• Title: [ICML 2023] Towards Controlled Data Augmentations for Active Learning
• Supplemental: [ go to the end of the paper ]
• Author Video: Link
• Code: GitHub

1. Introduction

Active Learning(AL) 에는 데이터 습득 단계가 바로 학습 loop* 안에 포함되어 있습니다.
*Active Learning 에서는 loop라는 표현을 자주 사용하는데요. 그 이유는 [ 학습 -> 습득 ] 이라는 일련의 단계를 하나의 주기로 여러번 반복되기 때문입니다. (아래 그림 참고)

AL의 학습 과정이 loop로 구성되어 있기 때문에, 10,000개의 데이터를 찾더라도 한번에 찾는 것이 아니라, 각각의 주기에서 1,000개씩 데이터를 찾아 10번을 반복합니다. 이렇게 가치 있는 데이터 샘플을 축적하고 모델을 업데이트하는 여러 주기로 분해함으로써, AL은 복잡성을 훨씬 낮추면서도 supervised-learning과 비슷한 성능을 달성할 수 있었습니다.
그동안 ‘AL에서는 왜 주기를 가지고 반복적으로 학습함?’이라는 질문을 종종 받았는데, 그에 대한 답변이 되었을 것 같습니다.

이렇게 주기학습으로 구성된 탓에, 초반부에 모델은 극히 적은 데이터를 가지고 모델 학습을 해야합니다. 이는 데이터 습득에도 영향을 주어 모델은 가치있는 데이터를 찾아내지 못하는 상황에 이를 수 있죠. 이는 소량의 데이터셋을 사용하는 모델에서 많이 발생하는 문제기도 합니다. 이렇게 적은 데이터로 학습할 경우 모델은 충분한 supervision을 갖지 못한 채 적은 데이터에 bias 되는 경향을 보이기도 합니다. 이는 결국 모델이 충분히 좋은 데이터를 선별하지 못해 성능의 저하로 이어질 수 있습니다.

이에 대한 해결책으로 저자는 Data augmentation을 선택했습니다. 데이터가 적으니 발생하는 문제였으니까요. 게다가 기존 연구에서도 augmentation으로 접근한 방식도 거의 없었습니다. 아래 [Fig. 1]은 저자가 Data augmentation을 적용하겠다고 영감을 얻은 간단한 실험 결과를 나타냅니다.

상단 [그림 1]에서 strength는 적용된 augmentation 기법의 개수입니다. (여러 개가 적용했을 때 더 많이 변형되니 strength라 표현한 것이겠죠) 이 때, flip, rotation 같이 아주아주 간단한 vanilla Data Augmentation (DA)을 적용하였습니다. 이렇게 vanilla DA를 강도별로 나눠서 실험해본 결과가 아래 ACC 입니다. 이를 통해 저자는 2가지 insight 를 찾았는데, 우선 하나는 성능이 향상되었다는 것입니다. 아주 나이브하게 augmentation만 적용해도 성능이 올랐다는 것이 눈에 띄는 차이입니다. 그리고 두번째가 핵심인데, 같은 augmentation이라도 lableded 와 unlabeled 에 서로 다른 효과가 발생한다는 것입니다. 보면 unlabeled 는 s가 4일 때, labeled 는 s가 2일 때, 그리고 둘 다 사용했을 때에는 s가 3일 때 성능 향상이 가장 컸습니다.
참고로 labeled는 (데이터의 가치를 판단하는) 모델을 학습할 때 사용되고, unlabeled는 (가치있는) 데이터를 습득할 때 사용됩니다.

굉장히 간단하면서도 재밌는 결과인데요. 저자는 이를 통해 DA를 AL에 결합할 때, labeled 와 unlabeled에는 서로 다른 augmentation 강도를 적용해야 한다는 결론을 찾았습니다. 특히, labeled pool은 신뢰할 만한 classifier를 얻기 위해 label-preserving 증강을 선호하지만, unlabeled pool은 탐색되지 않은 분포를 최대한 넓히기 위해 상대적으로 더 공격적인 증강이 필요할 수 있다고 판단했습니다. 따라서 저자는 이를 반영한 Controllable Augmentation ManiPulator for Active Learning (CAMPAL)을 제안하였습니다. 해당 방법론의 핵심은 다음 3가지와 같습니다.

• labeled pool, unlabeled pool에서는 각자의 objective에 맞는 각각의 augmentation을 구성
• 적용된 augmentation에 최적의 강도를 찾는 ‘강도 최적화 방식’ 제안
• uncertatinty, diversity 기반 AL방법 모두를 고려한 acquisition 함수를 제안

2. Methodology

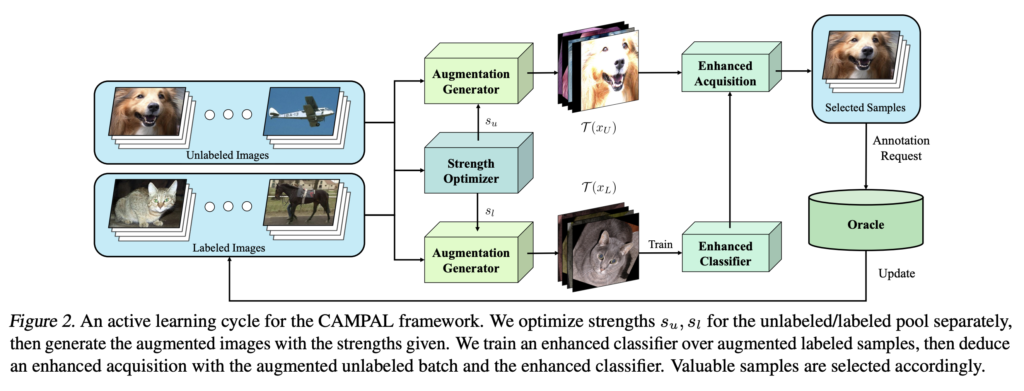
아래 [Figure 2]는 CAMPAL의 프레임워크를 보여줍니다. CAMPAL의 핵심 구성 설계 파트는 두 부분이라고 할 수 있습니다. 첫째, 구분되는 최적화 objective에 따라 labeled/unlabeled data pool에 독립적인 augmentation 강도가 조절되는 부분입니다. 아래 그림 중 Augmentation Generator와 Strength Optimizer가 여기에 해당됩니다. 둘째는 앞 부분 덕분에 조절된 aug. 기반으로 데이터를 수집하는 부분입니다. enhanced acquistion이 바로 여기에 해당됩니다. 이제 각 부분 별로 디테일한 내용을 다뤄보겠습니다.

2.1 Controllable Augmentations for Active Learning

앞서 Introduction에서 Labeled 와 Unlabeled 마다 aug. 기법을 다르게 적용해야함을 확인했습니다. 특히, Labeled의 경우 학습 때 사용도며, 모델의 예측 성능을 개선하여 신뢰할 수 있는 분류 모델을 구축하는 것을 목표로 합니다. (그래야 성능 향상에 도움이 되는 데이터를 정확하게 선별할 수 있겠죠?) 반면 Unlabeled 는 데이터셋의 분포를 더욱 확대하여 데이터마다 가지는 정확한 정보의 양을 추론하고, 이를 통해 더 나은 데이터 수집을 하도록 유도해야 합니다. 이렇게 labeled 와 unlabeled에 서로 다른 강도의 augmentation을 적용하기 위한 s에 대한 최적화 수식은 다음과 같습니다.

Strength for unlabeled data.

라벨이 없는 데이터를 aug. 목표는 결국 ‘풍부한 데이터 분포’ 입니다. 이를 통해 각 데이터가 가지는 정보의 양을 구하는 정확도를 향상시켜 더욱 신뢰할 만한 데이터 수집을 해야하죠. S가 너무 작으면, 분포는 거의 늘어나지 않을테고 S가 너무 커지면 과도한 분포 편차를 발생하여 잘못된 데이터를 수집할 수도 있습니다. 따라서 저자는 이 중간 어디의 적절한 정도를 아래[수식1]을 통해 도출하였습니다.

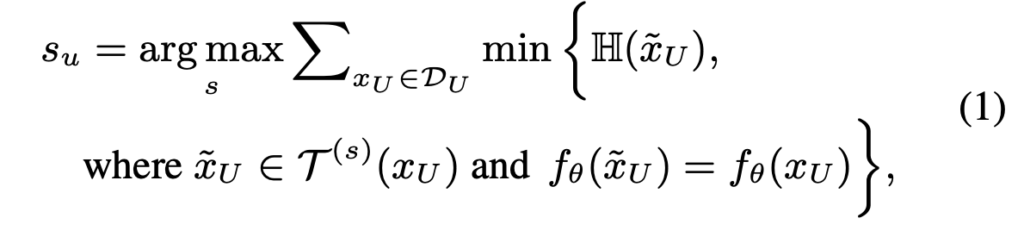
여기서 \mathbb{H}는 엔트로피를 나타냅니다. min{\mathbb{H}}을 통해 지나치게 aug.된 샘플로 인해 발생하는 distribution drift는 제거하는 동시에, 모든 unlabeled 의 min{\mathbb{H}}의 합을 최대로만드는 s찾음으써 데이터 전반이 가지는 정보의 양은 최대화하도록 설계하였습니다.

Strength for labeled data.

다음으로 Labeled는 aug.가 강력하게 되는 것을 지양한다고 했죠. 따라서 이 때의 s는 모델의 학습 안정성과 수렴이 더욱 잘되도록, aug.를 강하게 주지 않도록 설계하였습니다. 즉, augmentation이 적용되었다고 변환 전과 다른 output이 나오지 않도록 적절한 강도가 필요하죠. 이렇게 aug.된 이미지가 유사한 출력값이 나오도록 제어하기 위해 추가적인 손실함수가 필요합니다. 따라서 이를 고려한 가상의 loss \mathcal{L}_f를 정의하고, 이 \mathcal{L}_f를 최소화하는 s_l을 찾고자 하였습니다.

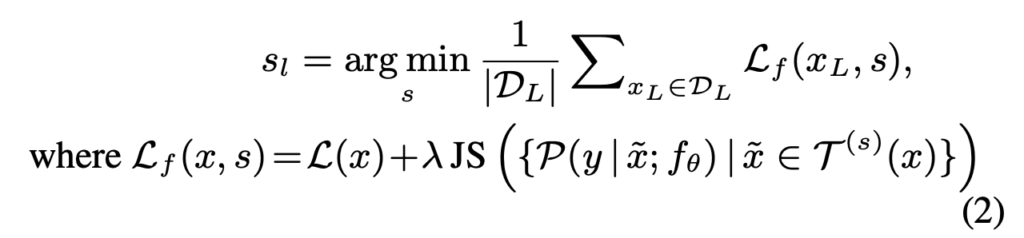
\mathcal{L}(x), \mathcal{L}_f(x)는 각각 일반적인 loss(여기서는 분류 문제니까 Cross entropy loss입니다)와 aug.에 대한 loss를 나타내며, \gamma는 고정 weight를 의미합니다. 해당 loss는 학습의 안정성과 수렴에 초점을 맞추기 때문에, aug.된 이미지가 증강 전과 유사한 출력을 발생하도록 확인할 수 있도록 Jensen-Shannon divergence(JS) term을 추가하였습니다. 즉, *JS는 두 분포가 얼마나 다른지 “dissimilarity”를 정량화하는 수식이라고 합니다.

*흔히 두 분포를 비교하는 수식에는 KL-divergence를 떠오르기 쉬운데요, JS는 여기에 거리의 개념을 도입한 것으로 symmetric하다는 특징을 가집니다. -> JS(P, Q) = JS(Q, P)
[참고] https://itsudit.medium.com/the-jensen-shannon-divergence-a-measure-of-distance-between-probability-distributions-23b2b1146550

지금까지 s_u, s_l을 구하는 법을 정의함으로써, augmentation의 정도를 조절하는 방법을 알아봤습니다. 다음으론 AL에 어떻게 결합할 지에 대해 다뤄보겠습니다.

2.2 Controllable Augmentation-induced Acquisition for Active Learning

Active Learning 은 그게 두 stream 으로 나뉩니다: uncertainty vs diversity. 쉽게 얘기하면 전자의 경우 “모델이 헷갈려하하는” 데이터를 찾는 것을, 후자는 “전체 데이터셋을 대표할 만한” 데이터를 찾는 것을 목표로 하죠. 접근법이 다르기 때문에 데이터를 수집하는 과정에서도 차이가 납니다. 전자는 모든 데이터셋에 대해 불확실한 정도를 점수화(score) 하고 sorting 하여 일정 개수를 선택하는 반면, 후자는 feature space에서 인스턴스 사이의 상관관계(보통 거리)를 측정하여 일정 개수를 선택합니다. 이렇게 다른 stream이다 보니, 기존 연구진들은 굳이 통합하는 방식 혹은 양쪽에 적용하는 방식을 제안하지는 않았지만, 저자는 모든 기법에 적용하는 방식을 알려줌으로써, AL에서 CAMPAL이 일반화될 수 있음을 강조하였습니다.

Integrating augmentations into score-based acquisitions.

먼저 Uncertainty 기반의 방법론에 적용하는 법에 대한 설명입니다. DA를 AL에 통합하기 위해, 모든 aug.된 데이터 \tilde{x}에 대해 정보의 양에 대한 score h_{base}를 계산한 다음, 이를 하나의 점수로 합산하는 방식을 취하였습니다. 이 때 몇 가지 추가 변형은 다음과 같습니다.

Integrating augmentations into representation-based acquisitions.

이번에는 diversity 기반의 AL에 접목하는 방식입니다. 기존 방법들은 feature space 상에서의 인스턴스 간의 상관관계를 측정하기 위해 거리 함수를 사용합니다. 그러나 저자는 개별 샘플 간의 거리 함수를 augmentation 된 샘플 간의 point-set distance 함수로 일반화합니다. 이렇게 설정된 거리 함수를 사용하여, 저자는 서로 다른 샘플에 대한 augmentation 간의 상관관계를 고려할 수 있었다고 합니다.

CAMPAL의 수도 코드를 통해 위에서 설명한 파이프라인을 요약하며 설명은 마무리하겠습니다.

먼저 적절하게 조절된 strength로 labeled data에 augmentation 버전 T_l을 생성한 다음, 이를 통해 classifier f_θ를 학습합니다. 이 과정을 통해 라벨링된 정보가 부족한 부분을 보완하고 더욱 신뢰할 수 있는 모델을 구축할 수 있습니다. 다음으로, 최적화된 strength s_u로 unlabeled의 augmentation 버전 T_u와 f_θ로 향상된 acquisition h_{acq}를 도출해냅니다. 특히 CAMPAL은 여러 주기에 걸쳐 aug.에 대한 dynamic strength를 제공하여 변화하는 데이터 풀에 맞게 스스로 조절하는 controllable acquisition을 유도합니다. 이 augmentation-induced acquisition 단계는 정확한 정보의 양에 대한 평가를 제공하고 augmentation의 긍정적인 영향을 보장하여 최종적으로 더 나은 데이터 선별 및 결과를 발생하는 데 도움이 될 수 있었다고 합니다.

Experiments

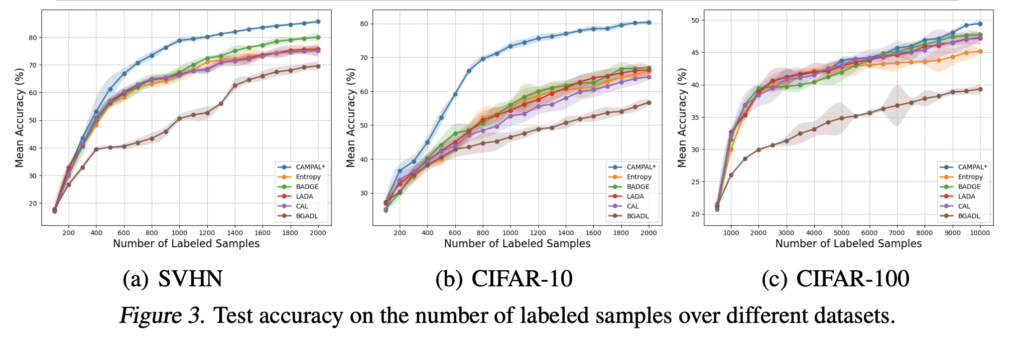
두 가지의 stream 이 다 등장한 만큼, 실험에서도 다양한 데이터셋과 다양한 기법(acquisition function)이 적용된 방법론을 기반으로 성능을 평가하였습니다.

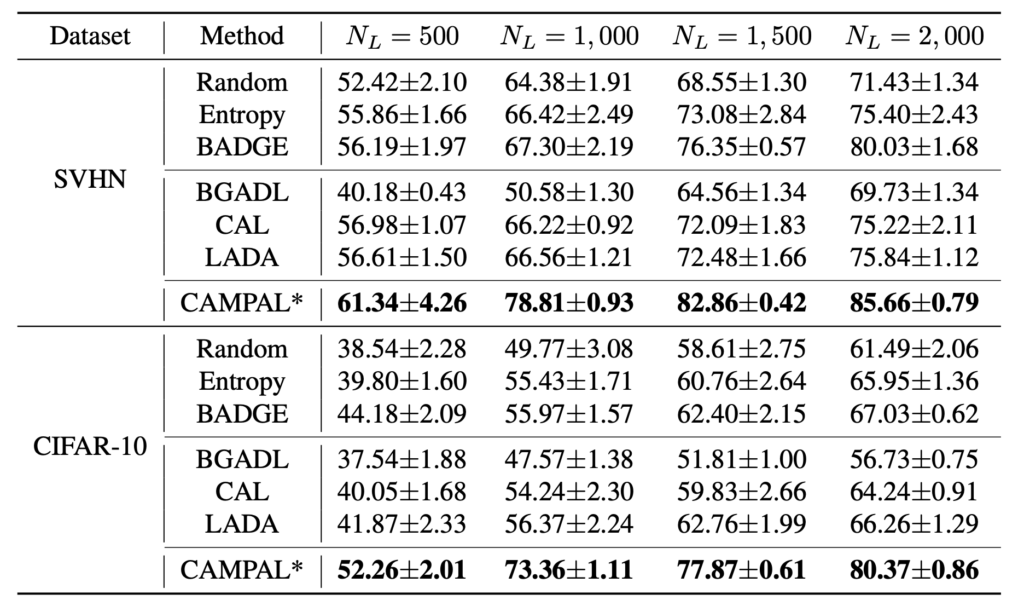
결론부터 말씀드리면, CAMPAL은 SOTA 를 보였고, 아래 [Table1] 과 [figure 3] 에서 확인할 수 있습니다. 특히 CIFAR-10 데이터셋의 500, 1000, 1500, 2000 개에서 각각 8.08%, 16.99%, 15.11%, 13.34%의 향상폭을 보였습니다.

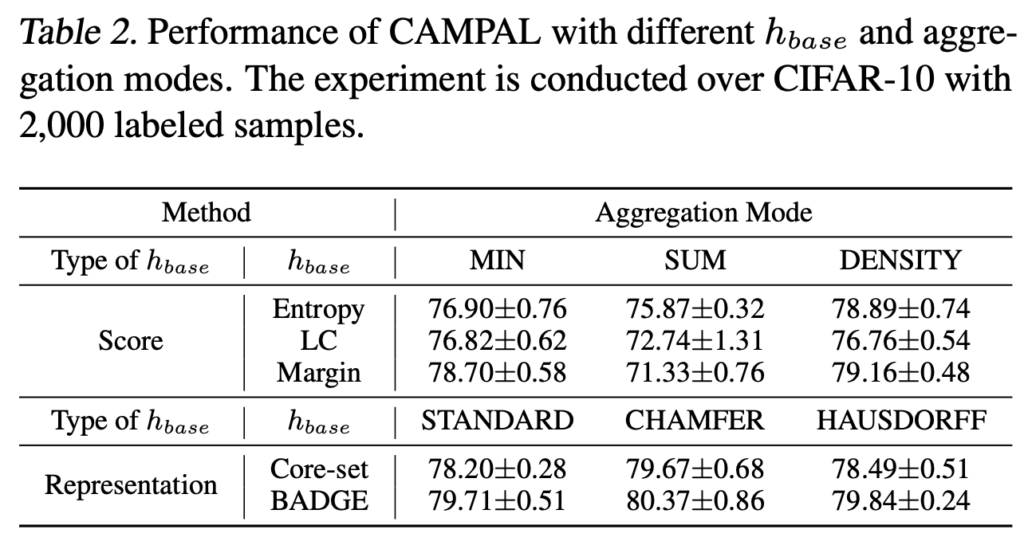
뿐만아니라, 2.2 Controllable Augmentation-induced Acquisition for Active Learning에서는 acquisition function을 각각 3가지 변형에 대해 제안했는데요. 두 가지 스트림에 대한 각방법론의 평가결과도 리포팅 하였습니다.

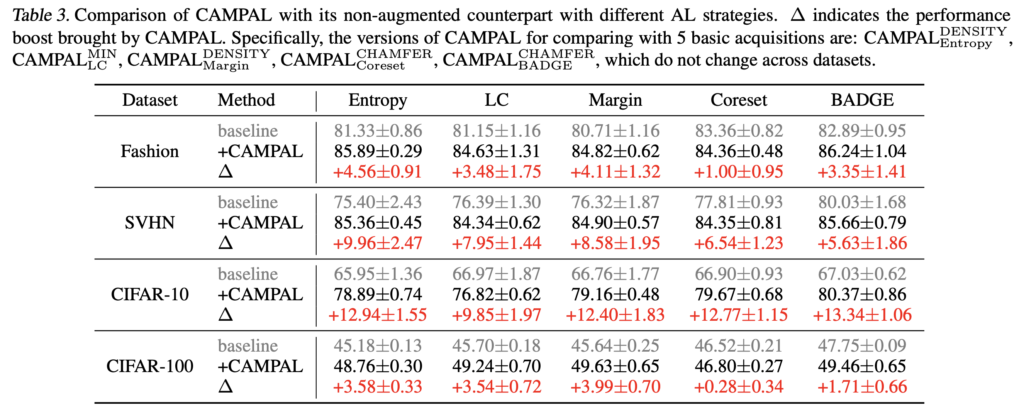
또한 [표 3]에서 볼 수 있듯이, 베이스라인과 다양한 데이터셋 실험에서 CAMPAL이 적용된 것이 가장 우수한 성능을 보여줍니다. 특히 CAMPAL은 일관된 성능 향상 효과도 보였습니다.

---