오늘은 시간적 정보를 가이드하는 부분을 포함해서 학습하는 SSL 논문을 가져왔습니다.
Introduction
Temporal한 정보가 Video에 도움이 되는지 되지 않는지에 대한 많은 연구들이 있습니다. 어떻게 학습을 하는지에 따라 차이가 있겠지만, 최근 연구에서는 “잘” 학습을 하면 도움이 된다는 결론이 슬슬 나고 있는 것 같습니다. 아무튼 이 논문도 명확한 Temporal한 정보를 가이드로 활용하는 논문입니다.
아무튼… 이미지 기반 연구들에서 augmentation을 적용하고 constrastive learning을 수행하는 방법론들이 좋은 성능을 보여왔던 것 처럼, video에서도 temporal shift를 적용해서 시간적 변화에 불변하는 표현력을 학습하는 연구 동향들이 이어져왔습니다.
하지만 temporal한 관계가 중요한 downstream task에서는 이러한 부분들이 중요한 정보를 무시하는 문제가 되는데요. 이 논문에서는 Toyota Smarthome 데이터셋이라고 집안에 설치된 홈캠에서 촬영된 영상으로 구성된 데이터 셋을 활용합니다. (물론 UCF, HMDB와 같은 데이터 셋으로도 평가를 진행합니다.) 따라서 해당 데이터셋에 포함되어 있는 특정 케이스(들어오고 나가는 장면들)이 보다 더 temporal한 순서에 민감하게 반응하여, 이 중요한 정보를 무시하는 문제점이 더 크게 부각이 되는 상황인데요.
본 논문에서는 Latent Time Navigation(LTN)을 제안하여 이 문제를 해결하고자 합니다. LTN은 contrastive 학습 과정에 시간을 인식할 수 있는 표현력을 학습하기 위해서 간결화된 시간 파라미터 매커니즘을 사용하는데요.
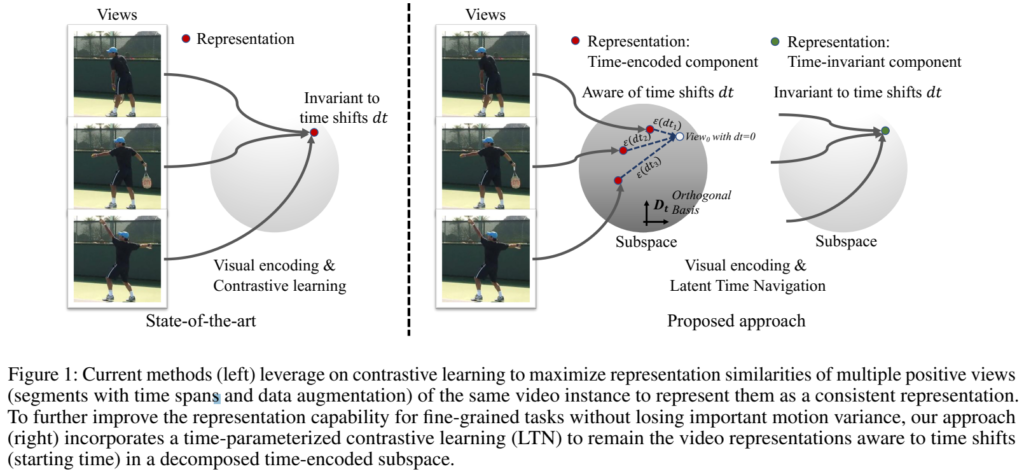
기존의 방법론들이 [그림 1]의 왼쪽과 같이 학습했다면, 이 방법론은 [그림 1]의 오른쪽과 같이 학습하는 방식입니다. 기존 방식은 여러분들 모두 아실 것 같은 MoCo같은 방법론이라고 생각하시면 되고요. LTN은 이제 그림이 2개로 나뉘어 지는 것과 같이 2개의 요소를 가집니다.
- “time-encoded component” : 이 요소는 직교 기저(orthogonal basis)와 그 magnitude의 선형 결합으로 시간 정보를 인코딩합니다.
- “time-invariant component” : 기존의 학습 방식(Anchor-Positive 두는 SSL 학습에서 쓰는 feature들)과 동일하다고 보면 될 것 같습니다.
그럼 이제 이 두 요소를 가지고 어떻게 학습을 하느냐면… 그건 이제 그냥 contrastive learning을 수행하는데요. 학습 자체는 “time-invariant component”로 수행하지만, 그 와중에 “time-encoded component”가 가지고 있는 시간 인식 정보를 보존하는 것을 목표로 합니다.
그래서 Contribution을 요약하면 아래와 같습니다.
- LTN을 제안하고, LTN이 효율적임을 보임
- Real-world dataset (Toyota Smarthome)의 SOTA 달성
- K400에서 학습하고, UCF101/HMDB51에서 평가하는 상황에서 높은 일반화 성능을 보임
Proposed Approach
LTN의 목표는 motion 정보를 알고있는 video representation을 time parameterization을 통해 학습하는 것인데요. 본격적인 구조를 알아봅시다.
Overall Architecture of LTN
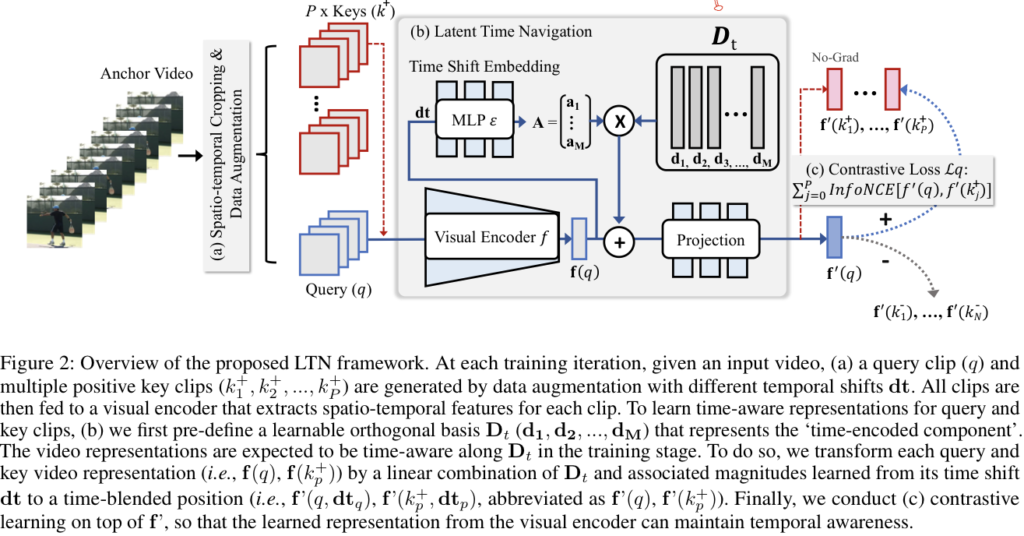
[그림 2]를 보면 전반적인 구조를 확인할 수 있습니다. 구조는 (a) 부터 (c) 까지 3단계로 구분되는데요. 일단 전반적인 구조를 보면 대충 느낌이 오겠지만, 뭔가 추가적인 encoder-decoder가 붙는 구조는 아니고, 일반적인 visual encoder 구조에서 학습 방법을 추가해서 잘 학습해보겠다는 구조인데요. 우선, 입력 영상에 data augmetation을 적용해서 Query 영상과 Positive 영상들을 생성합니다. 이런 방식들을 보면 Augmentation을 어떻게 주는지도 하나의 contribution으로 가져가던데, 이 방법론에서는 그냥 기존의 방법론(MoCo 등등)과 동일한 방식을 유지했다고 합니다.
다음 단계인 LTN에서는 이제 좀 복잡해지는데요. 앞선 단계에서 적용한 temporal augmentation과 ”time-encoded component”를 융합하기 위해서 추가적인 time parameterization 모듈을 추가한 설계입니다. 마지막으로는 이제 constrastive learning을 수행해야하는데, 이건 그냥 InfoNCE랑 동일한데요. 결론적으로는 이 중간 모듈에 모든 contribution이 다 들어있다고 보면 됩니다. 그럼 이제 본격적으로 자세하게 알아봅시다.
View Generation and Embedding
이부분에서는 기존 연구를 이어서 활용합니다. 우선 spatio-temorally crop을 적용하는데요. 이건 같은 비디오 내에서 랜덤으로 세그먼트를 고르고, 그 세그먼트 내에서 고정된 크기의 박스만큼 자르는 방법입니다. (기존 연구에서는 MoCo나 BYOL같은 방법론에 적용했을 때 성능향상이 있었습니다.) 그리고 추가적으로 이번엔 진짜 MoCo에서 쓰는 일반적인 augmentation 방식인 horizontal flip, color distortion, gaussian blur 등등을 랜덤하게 적용해줬다고 합니다.
본 연구에서는 query clip을 q로 정의하고, 여러개의 positive key들을 k^+_1,...,k^+_p로 정의합니다. 이때 positive key들은 temporal span이 길어야 좋다고 해서 길게 뽑아줬다고 하네요. Visual encoder로는 3D-CNN을 사용했고, 얘는 f(q)와 같이 정의합니다.
Awarness of Time in Latent Space
비디오는 수많은 프레임들의 연속으로 볼 수 있습니다. 프레임들끼리의 간격이 짧다면 유사한 영상일 확률이 높아지지만, 유의미하게 긴 간격을 가지고 있다면 분명한 차이가 있습니다. 이러한 맥락에 따라 모든 positive pair에 대해 f(q)를 직접적으로 매칭시키면, 시간 흐름에 따른 모션 정보를 상실하는 표현력을 학습하게 됩니다.
따라서 이 논문에서는 불변하는 특성들은 유지하면서도, data augmentation에 사용되는 time shift value(dt_q)를 인코딩하는 다양한 time parameterization 방법론들을 제안했습니다. 예를 들어, 특정 쿼리 영상과 positive key들에 대한 계산이라고 하면, f'(q,dt_q), f'(k^+_p,dt_p)와 같이 계산된다고 보면 됩니다. 이 두 representation은 이제 contrastive learning으로 계산될 수 있고요.
Time Parameterization in Latent Space
사실 이 부분이 이 논문의 핵심 파트 같습니다. 결국은 이 “시간 정보“를 어떻게든 정의했기 때문에 이 모든 것이 가능했다는 것인데요. 지도학습이 아닌 이상에야, 어떻게든 시그널을 주는 것이 중요하기 때문에… 핵심 파트가 되겠습니다.
Latent Space Decomposition
일단 repesentation space를 분해해야합니다. 이를 위해서 학습 가능한 orthogonal basis D_t = \{d_1, d_2, ..., d_M\} \;with \; M\in [1,dim) \; and \; d\in \R^{dim \times 1}을 정의해서 “time-encoded component”를 정의합니다. 이때 각각의 벡터 d_M은 기본적인 시각 변환 정도를 나타내게 됩니다. (시각적인 변환 정도는 N번째 프레임으로부터 0번째 프레임을 만들기 위한 변환 정도라고 보시면 됩니다. 이 정보를 알고 있다면, 값이 크면 시간적으로 먼 프레임이고, 작으면 가까운 프레임으로 볼 수 있겠죠? 이 정도를 이용해서 시간 흐름을 파악한다는 뜻입니다.)
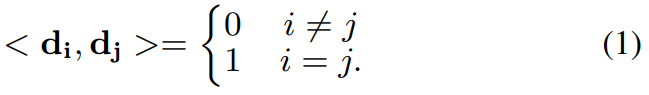
이 D_t는 직교 기저를 따르기 때문에, 두 방향 d_i, d_j는 [수식 1]의 조건을 만족하게 됩니다. 또한 직교성을 만족하기 위해서, forward 과정에서 Gram-Schmidt algorithm을 적용해줍니다. 이 방식의 기본적인 아이디어는 “ICLR 2022 : LATENT IMAGE ANIMATOR: LEARNING TO ANIMATE IMAGES VIA LATENT SPACE NAVIGATION”의 아이디어를 영상 단위로 확장한 것 같더군요. 관심 있으신 분은 이 논문도 참고 바랍니다.
Time Encoding
시간 변화에 따른 변화를 알아차리기 위해 “time-encoded component D_t”를 정의했습니다. 이제 남은 목표는 time shift value dt가 학습이 가능하도록 파라미터화하고, 이를 이용해서 인코딩 하는 것이 최종 목표가 됩니다.
그럼 이 d_t는 뭐길래 이 변화를 알아차릴 수 있는걸까요? 예시로는 영상의 특정 “refrence view”로 부터의 절대적인 시간 차이가 하나의 예시가 될 수 있습니다. 이 논문에서도 이 예시를 학습에 사용합니다.
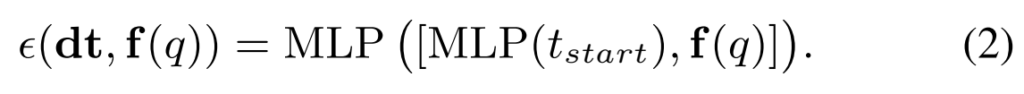
전반적인 수식은 [수식 2]와 같은데요. t_{start}는 reference view로 부터 얼마나 떨어져있는지를 나타내는 timestamp 값입니다. 이 timestamp 값과 쿼리 영상의 visual encoder feature를 함께 사용합니다. 쉽게 생각하면 그냥 너는 몇번째 프레임인지 알려주고 같이 학습하는 느낌이라고 보면 됩니다. 그럼 이제 이걸 어떻게 기존의 visual feature에 붙여서 학습을 시킬 수 있을까요? 논문에서는 3가지 방식을 제안합니다.
Variant 1. Time-driven Linear Addition
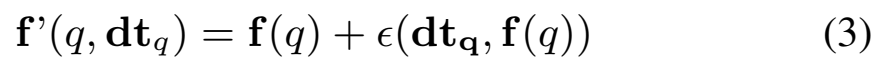
첫번째 방법으로는 D_t를 학습하는 과정 없이 단순하게 더한다는 생각을 해볼 수 있습니다. \epsilon(dt_q, f(q)) \in \R^{1\times dim}은 결국은 이 하나하나의 값들이 timestamp에 따른 변화량이기 때문에, 시간 정보가 결합된 표현력을 얻기 위해 학습해야하는 정보를 담고 있는 일종의 offset으로 생각해볼 수 있습니다. 그래서 이렇게 더하는 방법을 고려해볼 수 있고요.
Variant 2. Time-driven Attention
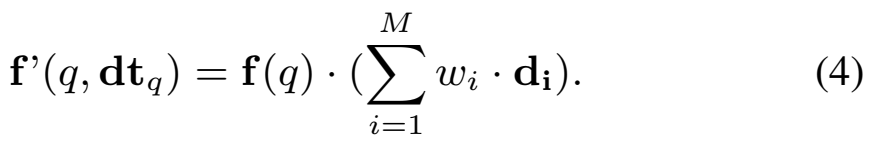
두번째 방법으로는 Attention이 있습니다. positive pair들의 attention weight set을 W \in \R^{1\times M} = \{w_1, w_2,...,w_M\} = Softmax(\epsilon(dt_q, f(q)))와 같이 정의할 수 있습니다. 이건 이제 1번 방법과 유사하지만, 특정 시간 인코딩 정보에 좀 더 집중하게 만드는 학습 방식 정도로 볼 수 있겠죠?
Variant 3. Time-driven Linear Transformation
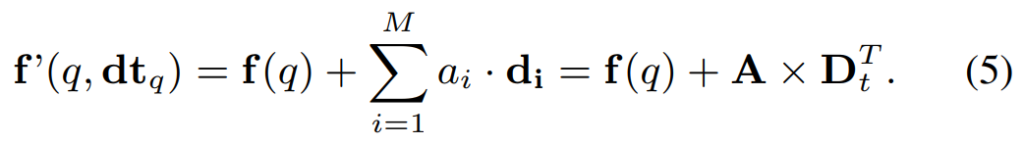
마지막 방법은 [그림 2]에 있는 것과 같은 모습인데요. 이 논문에서 제안하는 선형 변환 방식입니다. (사실 위의 2개 방법은 비교군입니다.) 선형 변환을 학습하기 위해서 D_t의 방향의 계수를 학습하는데요. 이걸 여기서 A \in \R^{1 \times M} = \{a_1, a_2, ..., a_M\} = \epsilon(dt_q, f(q))로 정의합니다. 이 변환은 시간 차이에 따라 변하는 representation들의 분산을 강제하는 식으로 학습을 수행하는데요. [그림 2]에 있는 것과 같이 visual feature는 visual feature대로 학습하면서, 순서만 학습한다고 보면 될 것 같네요.
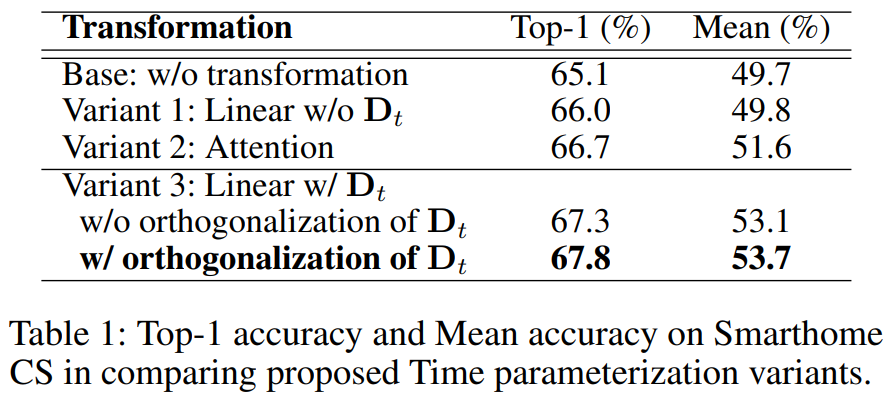
그래서 최종적으로는 제안하는 모든 방법이 학습에서 성능을 올리는 방향으로 진행되었다고 합니다. 이렇게 직접적으로 시간 정보를 가이드 하는 방식 자체가 효율적임을 입증하는 동시에, 본인들이 제안하는 선형 변환이 성능이 제일 좋은 것도 보이고 있네요.
Self-supervised Contrastive Learning
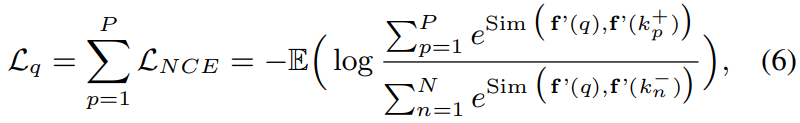
그래서 최종적인 학습은 InfoNCE Loss를 통해서 진행됩니다. Negative는 이제… 본인 빼고 나머지이기 때문에 자세한 설명은 다들 아실거라 넘어가겠습니다.
Experiments
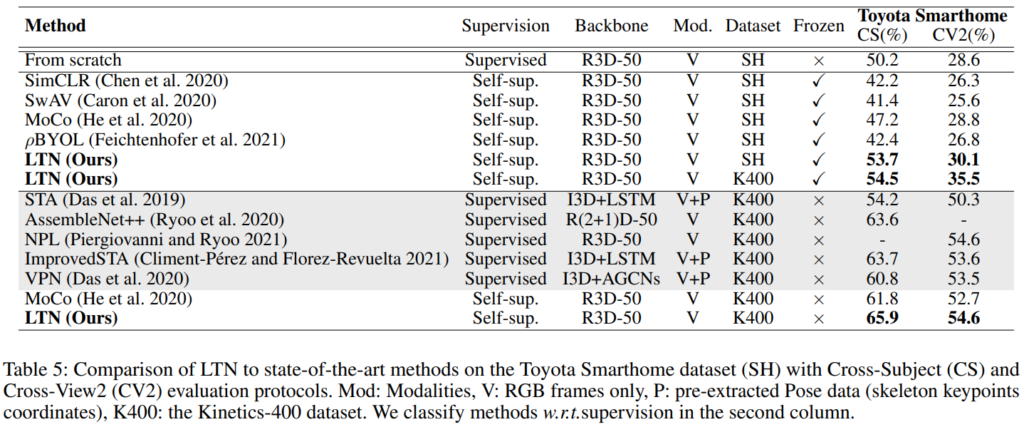
먼저 [표 5]는 Toyota smarthome 데이터 셋에서의 성능인데요. 사실 최근 연구가 없는 것을 보아… 잘 안쓰는 데이터셋 같기는 한데, 아무튼 추가 모달리티를 사용하는 기존의 지도학습 방법론 보다 더 좋은 성능을 보여주고 있습니다. (참고로 연구비 펀딩이 도요타 입니다 ㅎㅎ) 얘는 사실 더 볼… 부분이 없는 것 같고…
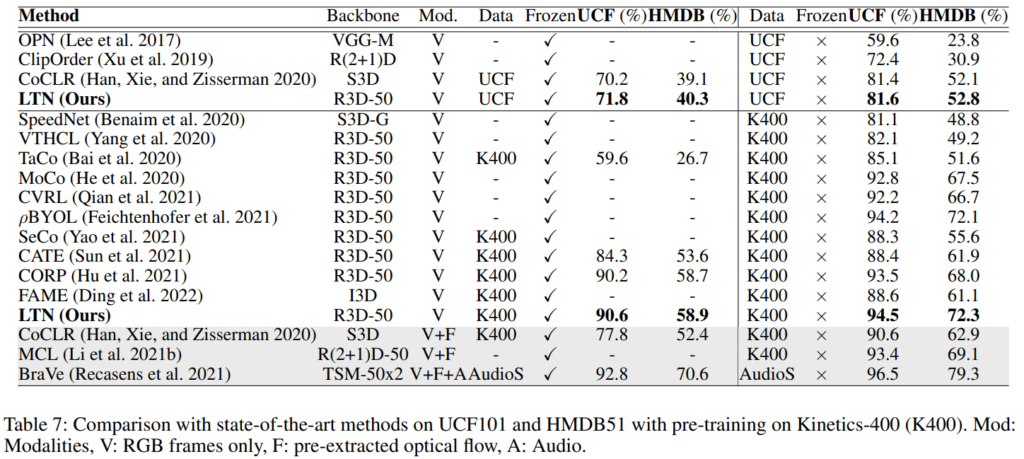
일반적으로 많이 비교하는 벤치마크 테이블은 [표 7]입니다. 비교군들의 성능과 대조를 해봐도 꽤 준수한 성능을 보입니다. (참고로 세팅은 똑같이 맞추고 실험을 수행한 것 같네요)
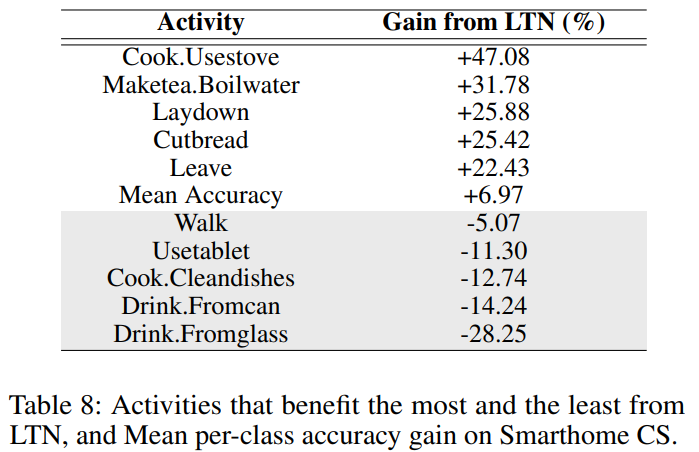
[표 8]은 smarthome 데이터셋에서 클래스별 성능을 보여주는 표입니다. 성능을 올리는 클래스와 낮추는 클래스가 구분되는 것을 볼 수 있는데요. 이렇게 어떤것은 오르고 안오르는 이유를 분석해보면, LTN은 인간의 행동을 중점적으로 고려하기 때문으로 해석할 수 있습니다. 예를 들어, “Drink” 클래스를 보면 어떤 것을 마시는지를 보지 않기 때문에 공통적인 성능 저하가 발생하는 것을 볼 수 있습니다.
Conclusion
AAAI 논문들이 짧아서 그런지 내용 압축이 많이 되어있네요. 일단 왜 orthogonal을 쓰는지…? 부터 컨셉 자체는 이해를 하겠는데 수학적으로 왜 이렇게 되는건지 이해가 어렵네요. 원 논문에서는 시간 축이 존재하지 않은 이미지에서 활용하는거라, 같이 읽어도 대체 왜인지… 이해가 잘 안됩니다. Time encoding 과정도 뭔가 Orthogonal가 연계된 정보를 쓸 것이라고 예상하면서 읽었는데 그냥 timestamp정보라서 novelty가 큰것 같다고 보이지도 않네요. 좀 더 분석이 있고 설명이 있으면 좋을 것 같은데 아쉬운 부분들이 있는 것 같습니다.
안녕하세요 좋은 리뷰 감사합니다.
수학적 내용들로 뭉쳐있어 이해하기 쉽지가 않네요..
1) 제가 논문의 컨셉 자체를 깊이 이해하지 못해서 생긴 것 같은데, 애초에 temporal modeling이 orthogonal과 관련 있는 이유가 무엇인가요?
2) 저자가 결국 사용하는 variant 3에서, A라는 D_t의 방향의 계수라는 것이 정확히 어떠한 방향으로 학습되도록 유도하는 것인지 잘 감이 안오는데, 학습을 통해 향하는 최적 A의 “방향”이 무엇을 의미하는지 궁금합니다.
3) 표 1에서 w/o orthogonalization of D_t는 forwarding 시 Gram-Schmidt algorithm을 사용하지 않는 경우를 의미하는 것인가요?
1) 사실 저도 이해하는데 어려웠는데요. 둘은 관계가 없… 다고 봐야합니다. 제가 생각했을 때는, Orthogonal은 temporal modeling을 학습하기 위한 “수단” 중 하나 일 뿐입니다. 설명하기가 복잡한데, Orthogonal을 이용해서 timestamp를 학습하기 위해서 사용합니다. 왜인지는 이전 논문 봐야 100% 이해할 수 있는데, [그림 1]에서 오른쪽 그림에서 빨간 점들 보시면 대충 컨셉을 알 수 있습니다.
2) 저희 magnitude 쓰는거랑 비슷하게 생각하면 되는데요. “시간적 변화의 정도 = 크기” / “시간 변화 방향 = 방향”으로 보면 됩니다.
3) 눼 맞습니다.