가끔 분석 논문을 읽는데 오늘도 분석 + 개선 논문입니다. 읽느라 되게 오래걸렸는데… 최대한 정리 잘 해서 작성해보겠습니다.

Introduction

우리가 “트랜스포머”를 떠올리면 생각나는 몇가지 특징이 있습니다. 오늘 분석 논문에서는 “강인함”에 대해서 다루는데요. 강인하다는 것은… convolution을 쓰는 일반적인 신경망에 대비해서 생각해보면 되는데요. 트랜스포머(대표적으로 ViT)의 경우에는 self-attention을 통해서 non-local한 관계를 모델링하는 것에서 오는 여러가지 장점들 때문에, 일반적으로 강인하다고 생각되어 왔습니다. 근데 문제는… 최근에 ConvNeXt는 self-attention이 없이도 ViT 대비 일반성과 강인성에서 좋은 모습을 보이고 있는데요. 이러한 관점에서 self-attention의 역할이 무엇인가… 에 대한 근본적인 질문을 해볼 타이밍입니다.

---

(중간 설명 시작) 강인함에 대한 예시는 위의 예시 그림을 보면 될 것 같네요. Citiscape dataset에서 segmentation 예시인데, 각종 노이즈에 얼마나 강인한지를 보여줍니다. Segformer가 기존 Transformer이고, FAN-S-H가 이 논문에서 제안하는 트랜스포머 모듈 구조를 적용한 방법론이라고 보시면 됩니다. (중간 설명 끝)

---

따라서, 본 논문에서는 ViT의 self-attention이 visual grouping을 통해 mid-level representation을 증강시킨다는 증명하기 위해서, spectral clustering을 통해서 ViT 모든 레이어의 output token을 분석했습니다. 그 결과 eigenvalues와 입력 변형에 따른 pertubation의 상관관계가 있다는 것을 보입니다.

왜 그룹핑이 되는가…? 에 대한 이해를 위해서는 Information bottleneck의 관점에서 self-attention 연산을 이해해야 합니다. Information bottleneck은 이제 특정 타겟 라벨과 feature 표현력에 사이의 상호 정보량을 최소화하는 방향으로 중요하지않은 정보량을 압축하는 과정이라고 보면 됩니다. 이러한 이유에 따라, self-attention 자체를 “Information bottleneck의 반복적인 최적화 단계”로 재해석 할 수 있습니다. 즉, Information bottleneck 자체가 클러스터링을 장려하는 방향이기 때문에, 왜 그룹핑이 되는지를 해석할 수 있다는 것이죠.

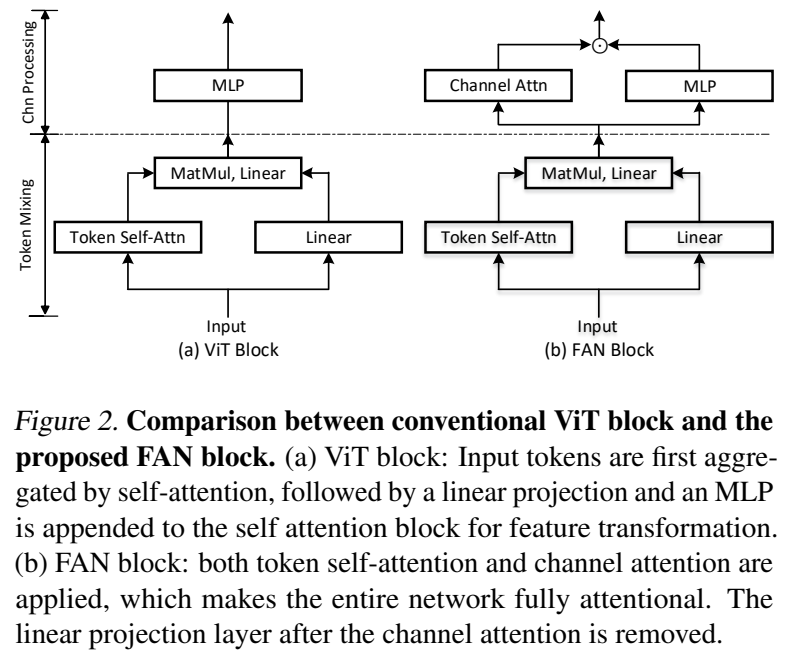
[그림 2]를 보면, ViT는 MLP 레이어의 중첩으로 정보를 aggregate 하지만, 이 논문에서 제안하는 FAN(Fully Attentional Networks) block은 채널 어탠션 연산이 추가되어 있습니다. 이는 그룹핑과 강건함을 모두 강화하는 aggregation 방법이라고 하네요.

따라서 분석만 하는 논문은 아니고, 분석 결과를 바탕으로 좀 더 강인하게 작동하는 FAN 블럭을 제안했다로 이해하면 될 것 같고, Contribution은 아래와 같습니다.

• 그룹핑, information bottleneck 그리고 강인한 일반화성(generalization)을 통합하는 실험적인 프레임워크 제공
• 제안하는 FAN 블럭은 아주 약간의 cost만으로 성능을 올릴 수 있을 정도로 효율적으로 제안됨
• (Robustness에 관한) 수많은 실험!

Fully Attentional Networks

ViT의 특성들을 information bottleneck의 특성으로 치환해서 설명을 해보는 섹션입니다. 그래서 FAN

Preliminaries on Vision Transformers

[그림 2]의 왼쪽 그림이 ViT 블럭 구조입니다. 사실 이 구조는 대부분 아시죠? Notation만 대충 정의하고 넘어가자면… 이미지를 n개의 패치로 균일하게 쪼갰다고 가정하고, token embedding x_i \in \R^d, i=1,...,n로 각 패치를 인코딩 할 수 있고, 이를 입력으로 사용합니다. 자세한 구조를 천천히 톺아보면…

Token mixing

Token mixing 단계에서는 global information을 self-attention을 통해 aggregate합니다. 입력 토큰이 X = [x_1,...,x_n] \in \R^{d \times n }이라고 가정했을 때, self-attention에는 당연히 각각의 파라미터 W_K, W_Q, W_V가 있겠죠? 그리고 각각에 대응되는 임베딩 K = W_KX \in \R^{d \times n},Q = W_QX \in \R^{d \times n},V = W_VX \in \R^{d \times n}이 존재합니다.

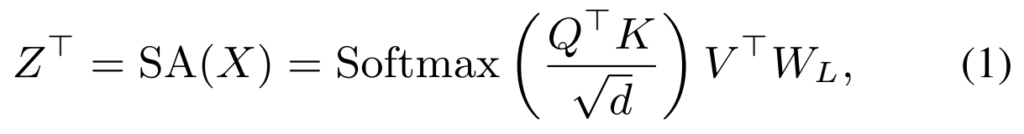
그때 self-attention 모듈이 token feature를 aggregation하고 attention 연산을 수행하는 과정이 [수식 1]이라고 볼 수 있습니다. W_L \in \R^{d \times d}의 경우에는 그림에 보면 있는 linear transformation이고요, Z = [z_1, ..., z_n]은 이제 aggregation된 token feature 마지막으로 \sqrt{d}는 스케일 펙터입니다.

Channel processing

[수식 2]는 Channel processing 단계에 해당하는 MLP 모듈입니다. 여긴… 그냥 MLP라 설명 패스하겠습니다.

Intriguing Properties of Self-Attention

ViT의 토큰 feature z가 의미있는 클러스터를 형성한다는 관찰에서부터… 시작해봅시다. 그럼 클러스터는 어떻게 관찰할 수 있을까요? 관찰은 S_{ij}=z_i^{\top}z_j로 token affinity matrix를 정의하는 Spectral clustering을 이용하여 클러스터를 관찰할 수 있습니다. 왜 관찰을 할 수 있냐면… 주요 클러스터의 갯수는 유의미한 eigenvalues의 다양성에 의해 추정될 수 있기 때문에 가능하다고 하네요. (사실 이부분은 이론적인 근거가 있는데, 저도 처음봐서 출처까지 가보지는 않았습니다)

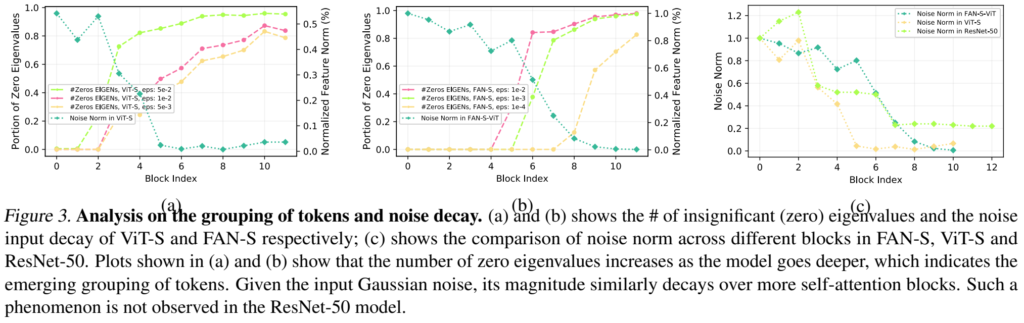
아무튼 그래서 ViT의 다양한 블럭들에서 eigenvalues를 시각화해보면 [그림 3-a]와 같은데요. 노이즈를 추가하면 추가할 수록, 유의미한 eigenvalue의 수가 급격하게 떨어진다는 것을 확인할 수 있습니다. 이러한 관찰은 중간 블록들에서 robustness와 그룹핑이 공존하고 있다는 것을 시사합니다.

---

(중간 설명 시작) 입력에 노이즈를 추가하는 것은 가우시안 노이즈를 추가하는 것입니다. 다른 의미로는 입력 데이터에 변형을 가하는 것인데요. 그림의 초록색 선이 해당 노이즈를 주었을 때, norm의 비율이라고 보면 됩니다. 나머지는 이제 eigenvalue에 대한 수치인데, 0이 되는 경우에 대해서 보여줍니다.

0이라는 것은 결론적으로는 데이터의 중요도가 낮다고 볼 수 있습니다. 그리고 그림을 보면 모델이 깊어질 수록 이 zero eigenvalues의 비율이 높다는 것은, 비슷한 종류의 데이터가 많이 있다는 것이고 따라서 노이즈는 줄어들고 그룹핑되어진 토큰의 숫자가 많다는 것으로 해석할 수 있습니다. (중간 설명 끝)

---

[그림 3-b]는 동일한 실험에서 FAN-S-ViT([그림 2]에서 제안된 블록 쓴 구조)의 실험도 보여주었고, [그림 3-c]는 Resnet50까지 있는 비교실험인데요. 이 실험들을 통해서 Resnet50의 robustness는 downsampling에서 생긴다는 것을 알 수 있으며, 최종적으로는 Resnet50의 노이즈가 덜 제거되는 것을 볼 수 있습니다.

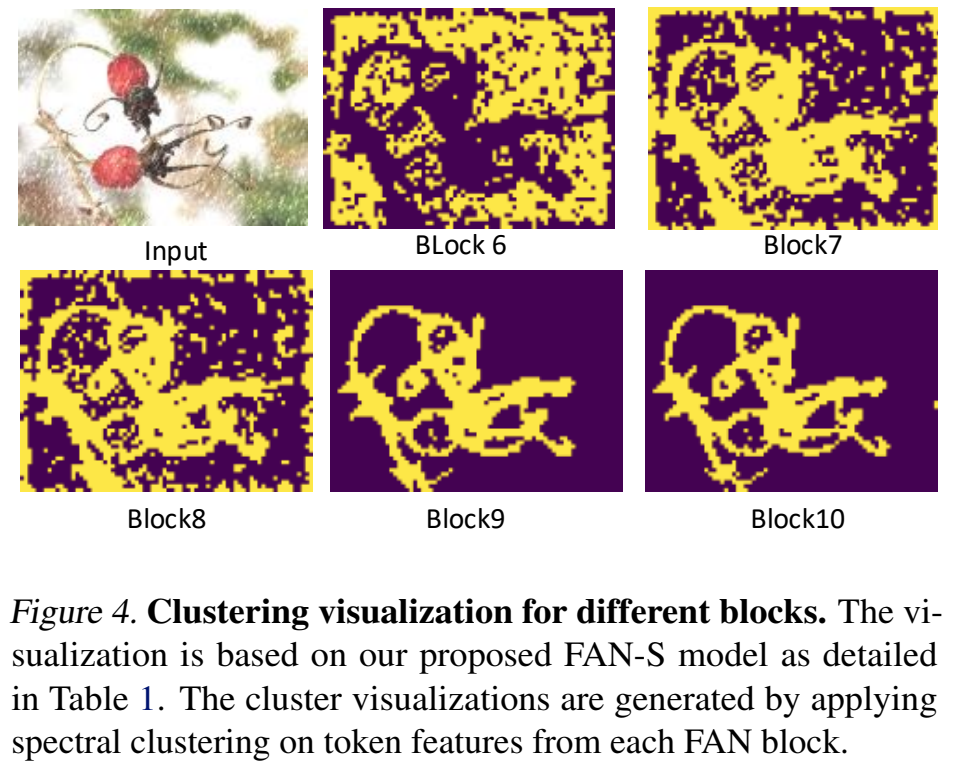
또한 [그림 4]를 통해서 실제로 시각화를 진행을 해보면, 중요하다고 판단되지 않는 영역에 대한 토큰들이 사라지는 것을 볼 수 있는데요. 이를 통해서 그룹핑이 진행된다고 볼 수 있습니다.

An Information Bottleneck Perspective

서론에서도 살짝 이야기하긴 했는데, 시각적 그룹핑은 손실 압축의 한 형태로 볼 수 있습니다. 그리고 이 손실 압축은 information bottleneck으로 볼 수 있어서 서로 같다고 볼 수 있는데요. 분포 X \sim N(X', \epsilon)가 있을 때, X는 노이지한 입력이고, X’은 출력값이라고 가정해봅시다. Information bottleneck은 X’을 예측하기 위해 X에 있는 유사한 정보들을 포함하는 Z를 찾아내는 f(Z|X)정의할 수 있는데요.

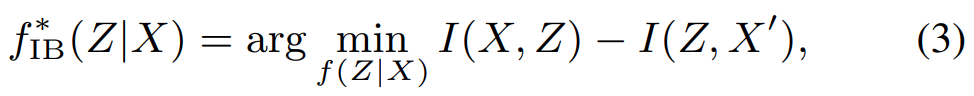
information-theoretic 최적화 문제로 이걸 정의하면 [수식 3]과 같다고 합니다. 함수 2개의 차이를 계산하는 건데, 앞의 함수가 정보량을 압축하는 목표이고 뒤의 함수가 연관있는 정보를 보존하는 목표를 가지고 있게 되어있는데요. 사실 저도 처음봐서 뭐… 이거다 싶은 느낌은 없는데 이런 것들이 원래 있었고, self-attention 연산과 관련지을 수 있다 정도만 알면 될 것 같습니다.

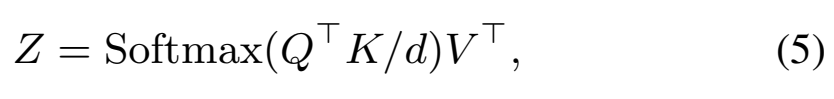
Self-attention block에서는 output features Z = [z_1,...,z_n] \in \R^{d \times n}이고 input X = [x_1,...,x_n] \in \R^{d \times n}이라고 가정했을 때, [수식 5]와 같이 정의됩니다.

Remark

그럼 모양도 다른 두 수식이 왜 연관될 수 있을까요? Self-attention은 Information bottleneck의 원리에 따라 토큰을 업데이트합니다. K는 클러스터 중심점 feature \mu_c를 저장하고, 입력 feature x는 softmax를 통해서 그들을 클러스터링합니다. 그리고 새로운 클러스터 중심점 z는 갱신된 token feature가 되고요. (토큰들을 학습하는 과정이 클러스터의 중심점을 학습하는 과정과 동일하다는 뜻) 따라서, 노이즈 필터링과 그룹핑을 장려하는 방향의 최적화 과정을 반복하는 것이 ViT의 self-attention 모듈의 집합이라고 정의할 수 있습니다. (수학적인 정의도 Supplementary에 포함되어 있는데요. 관심 있으시면 보시면 좋을 것 같습니다.)

Multi-head Self-attention (MHSA)

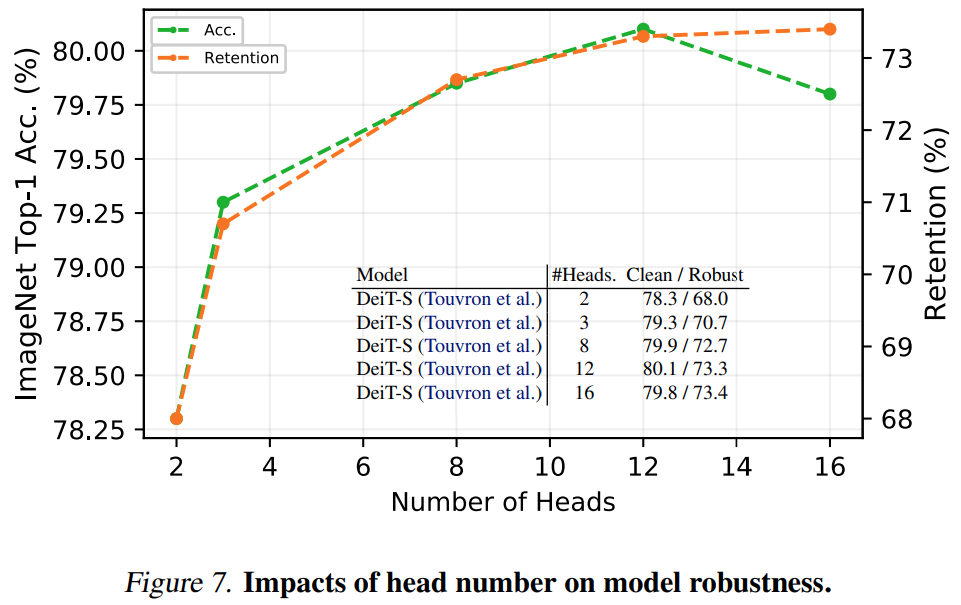
Self-attention의 MLP 레이어가 결국은 information bottleneck과 동일하다는 점에 대해서 지금까지 설명을 했고, 그런 관점에서 MHSA 자체도 information bottleneck의 혼합과 동일하다고 해석하고 있는데요. [그림 7]은 그런 관점에서 헤드의 수에 따른 정확도와 robustness에 상관관계를 보여줍니다. 일반적으로는 많아야 좋다고 하네요.

Fully Attentional Networks

서로 다른 헤드들을 묶으면서도 robust한 표현력을 강화하는 channel processing module을 디자인하기 위해서 이 논문에서는 두가지 방향으로 고민을 했는데요. 특정 헤드 혹은 채널은 확실한 정보를 더 캡쳐하기 때문에, 채널 reweighting을 도입해서 좀 더 구조적인 표현력을 증대하는 방향을 일단 고민을 했다고 하네요. 그러면서도 reweighting이 local한 채널만 보는게 아니라 좀 더 그룹화된 정보를 활용하기 위해서, 각 채널의 전체적인 공간을 봐야한다는 목적을 세웠는데요. 사실 요약하면 “Self-attention + Channel-attention”을 하겠다고 볼 수 있습니다.

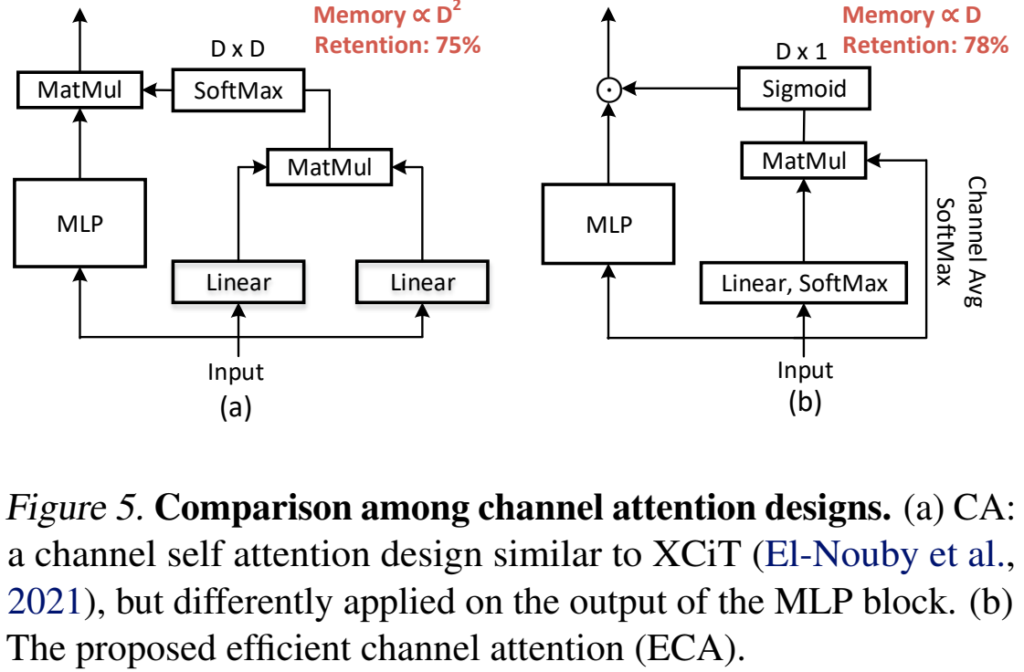
이런 흐름의 생각이 최초는 아니고, [그림 5-a]는 channel attention을 결합한 일반적인 예시와 같이 다른 방법론들도 존재합니다. 이 경우에는 D \times D의 channel attention matrix를 가집니다.

Attentional feature transformation

기존의 방식에서는 channel-attention을 아래와 같이 수행합니다.

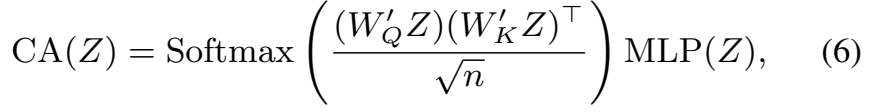
[그림 5-a]와 같이 보시면 좋은데요. (W가 붙을 경우 linear transformation 파라미터) 다들 잘 아시겠지만, self-attention과의 차이는 어디 축으로 attention을 주느냐가 있습니다. 당연히 channel-attention이니까… channel 축으로 연산을 수행하는데요. correlation이 낮은 이상치는 이제 낮아지고, correlation이 높은 값들은 aggregate됩니다. 이런 과정을 통해서 관계 없는 feature들에 대한 필터링을 수행하고, background & foreground 토큰에 대한 클러스터링을 더 정확하게 수행할 수 있게 합니다.

Efficient Channel Self-attention

그럼 새롭게 제안하는 Channel-attention 방식이 뭐가 더 좋아서 이렇게 쓰자는 걸까요?

첫번째 이유는 계산 복잡도입니다. [그림 5]에서도 메모리가 표시되어 있긴 해서 보신 분들도 있겠지만, D \times D만큼 필요하다는 것은 채널 X 채널 만큼 필요하다는 뜻입니다. 꽤 크죠? 알고리즘 측면에서 공간복잡도가 D^2에서 D로 변경되는 것은 큰 장점입니다.

두번째 이유는 계산 효율성입니다. 기존의 Self-attention 모듈은 학습 과정에서 일부 채널만 학습하게 됩니다. 이는 Attention weight가 생성될 때, softmax 연산이 적용되면서 작은 weight 값을 가지게 되면 곱해지면서 계속 사라지기 때문입니다.

이 두 문제를 해결하기 위해서 제안된 방식이 FAN block에서 쓰는 방식인데요.

먼저, Token feature끼리의 co-relation matrix를 계산하는 것이 아니라, 채널 축을 평균 해서 토큰 프로토타입 \bar{Z}, \bar{Z} \in R^{n \times 1}을 생성합니다. \bar{Z}는 각 토큰의 공간 정보를 채널축에 따라 모은거라서, 이 정보들은 token feature와 co-relation matrix를 계산하는데 쓸 수 있습니다.

다음으로는 Softmax 대신 normalize된 attention weight에 Sigmoid를 적용하고, Matmul 대신 multiply하는 차이점이 있습니다. 이 부분은 소수의 중요한 토큰만 학습하는 것을 방지하고, reweighting에서 공간적인 관계를 학습하는 방법입니다. (채널들은 실제로는 독립적이기 때문)

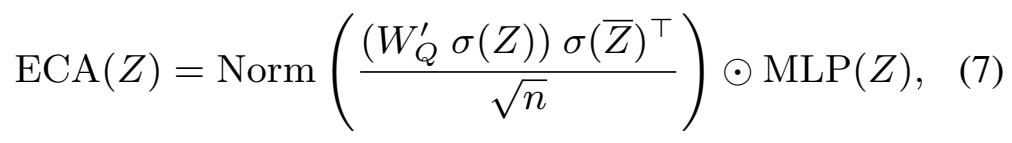
그래서 이 두 방식을 결합한 수식이 [수식 7]과 같은 구조이고, [그림 5-b]와 함께 보시면 되는데요. \sigma는 softmax 함수, Norm은 Sigmoid입니다. 이런 구조로 새로운 Self-attention + Channel-attention 모듈을 제안했다고 보면 될 것 같네요.

Experiments

시작하기전에… Metric이 아마 다들 처음 보시는게 많을 겁니다. 그래서 좀 정리하고 넘어가보죠.

• Retention rate R = Robust Acc./Clean Acc. = IN_C/IN_{1K}

Corruption되어 노이지한 이미지넷 성능과 클린 이미지넷 성능을 이용해 계산한 메트릭이라고 보면 됩니다.

• mCE (mean Corruption Error)

이 Metric은 ImageNet-C를 제안한 논문에서 제안한건데, 대충 보면… 당연히 모르겠지만 다양한 에러값에 대한 수치를 평균냈다. 그러니까 이 모델이 노이즈에 얼마나 강인한지 측정할 수 있다 정도로 알면 될 것 같습니다. (에러값에 대한 수치 평균이니까 낮을수록 좋음!)

Analysis

분석 파트 줄 설명이 너무 많아서… 사실 대부분은 반복이고 결론적으로는 Robustness에 강인한 모델을 잘 만들었다…가 결론이니까 염두해두고 보면 좋을 것 같습니다.

Effects of advanced training tricks

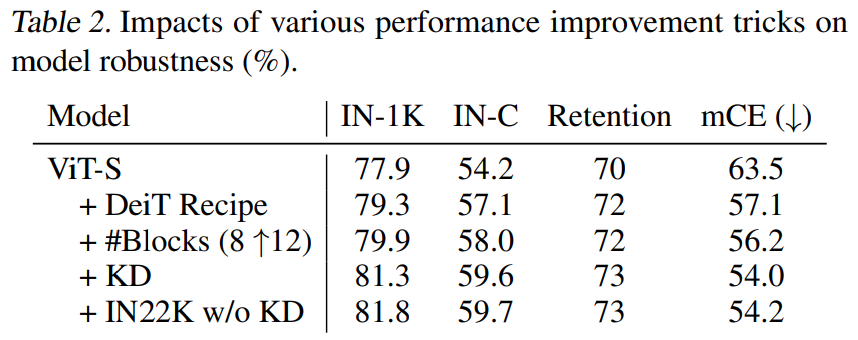
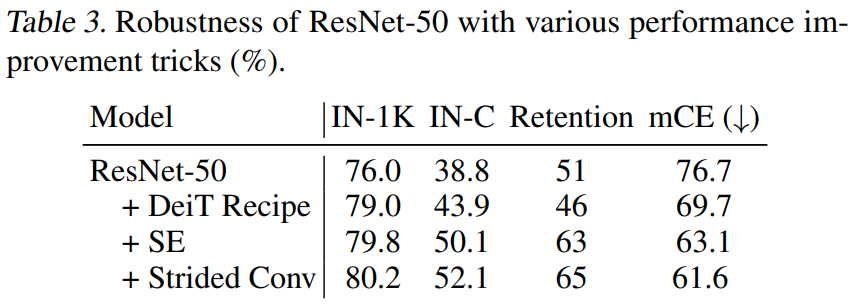
[표 2]와 [표 3]은 기존 ViT와 ResNet 모델에 각종 트릭을 적용해서 Robustness 성능을 향상시켜보는 과정입니다. 학습 과정에서 뭔가 변형을 줘서, 충분히 학습이 잘 되면 새로운 모델 구조를 제안해볼 필요가 없겠죠? 그래서 있는 과정 같은데요. 공통적으로 DeiT의 학습 방식 (CutMix와 RandAugmentation)을 적용했을 때 성능이 향상되었고, 나머지는 그냥 모델 구조에 맞춰서 좀 더 적용해봤을때 이정도 성능이 나온다고 보면 될 것 같습니다. 이후로 *을 붙이면 이제 이 학습 셋을 썻다 정도로 표기합니다.

Difference among ViT, SWIN-ViT and ConvNeXt

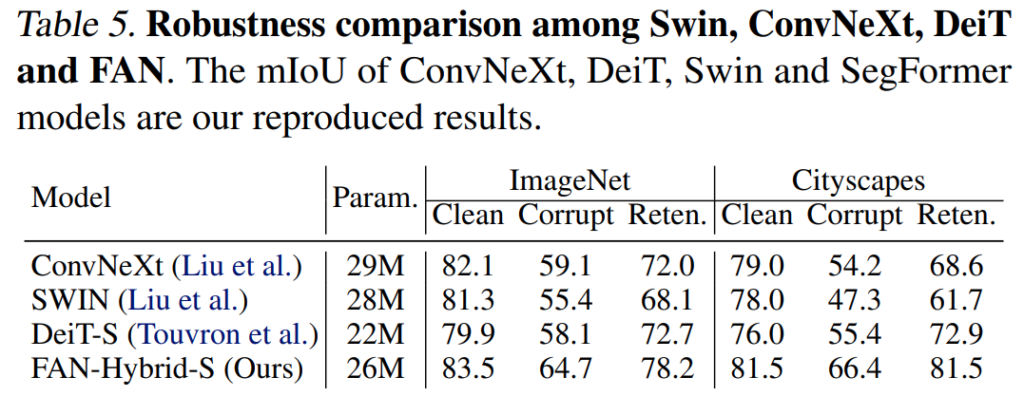
[표 5]는 이제 유명한 모델들 성능 비교해둔건데요. ConvNeXt가 SWIN 트랜스포머보다 훨씬 더 좋은 성능을 보입니다. 이게 최근 SOTA 트랜드라고 하는데요. 저자들은 이 이유가 SWIN 트랜스포머의 구조적인 문제 때문임을 지적합니다. 앞서 이제 information bottleneck 관점에서 설명한 내용을 쭉 다시 생각해보면, SWIN 트랜스포머는 구조적으로 윈도우 기반으로 local self-attention을 수행하죠? 이 과정에서 information bottleneck이 local한 정보만을 보도록 강제하기 때문에 이런 성능 하락이 발생한다고 합니다. 이런 사례를 통해서 은근히 global 정보(채널 축에 따른 attention)을 함께 수행하는 본인들 모델의 robustness 성능이 좋다는 것을 어필하는 것 같네요.

Fully Attentional Networks

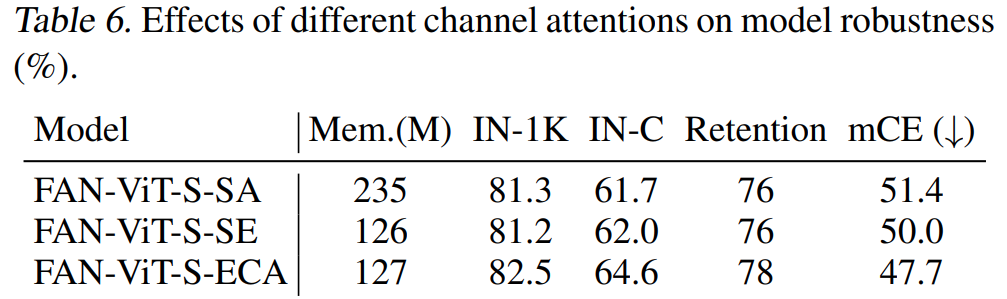
[표 6]은 Self-attention(SA), Squeeze-and-Excite attention(SE), Efficient channel attention (ECA / 제안하는 구조)에 따른 성능 차이와 GPU 메모리 차이를 보여줍니다. 높은 성능에 적은 메모리를 달성한 것을 볼 수 있는데요. 즉, 공간적인 관계를 고려하는 학습 방식이 더 좋다는 것을 볼 수 있습니다.

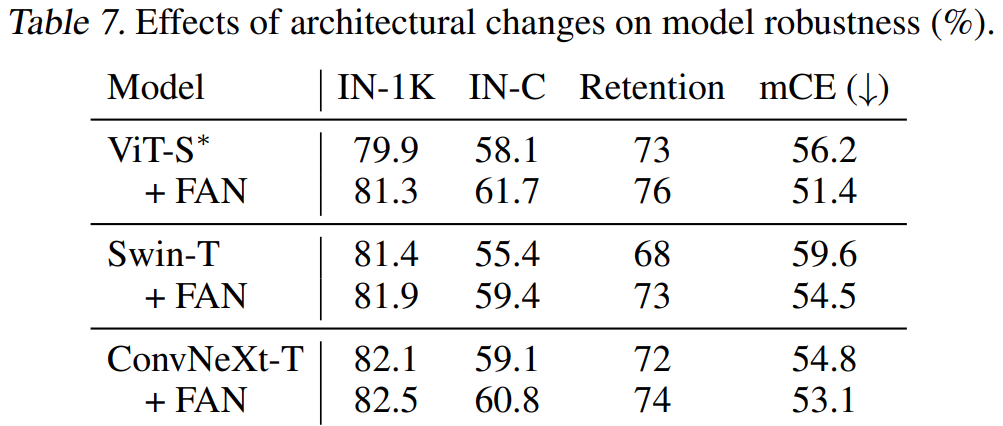
[표 7]은 이제 각종 기존 모델에 제안하는 모델을 붙이는건데요. 차이는 있지만 공통적으로 성능 향상을 보였습니다. 같은 트랜스포머 임에도 Swin 트랜스포머의 성능이 조금 낮은데요. 이건 SWIN 트랜스포머의 robustness 성능이 낮은 이유를 위에서 설명했는데 그거랑 비슷한 이유로 성능이 떨어졌다고 분석하는 것 같네요.

그리고 ConvNext와의 결합에서도 좋은 성능을 보이는데요. 일반적으로 FAN 모델의 상위 단계에서만 클러스터링이 중점적으로 진행되고, 하위 단계에서는 국소적인 시각적 특징을 추출하는 것에 집중한다는 것을 발견했습니다. ([그림 3]의 예시를 함께 보세요) 이런 분석에 따라 Down-sampling을 하위 두 단계의 conv 블록에 적용하고, conv stage의 출력에 FAN 블록을 추가했습니다. 이걸 FAN-Hybrid라고 제안하고, ConvNeXt에 적용해서 더 높아진 성능을 보입니다. 이를 통해서 CNN 기반의 모델에서도 동일한 방식으로 robustness를 향상시킬 수 있음을 보입니다.

Comparison to SOTAs on various tasks

Robustness in image classification

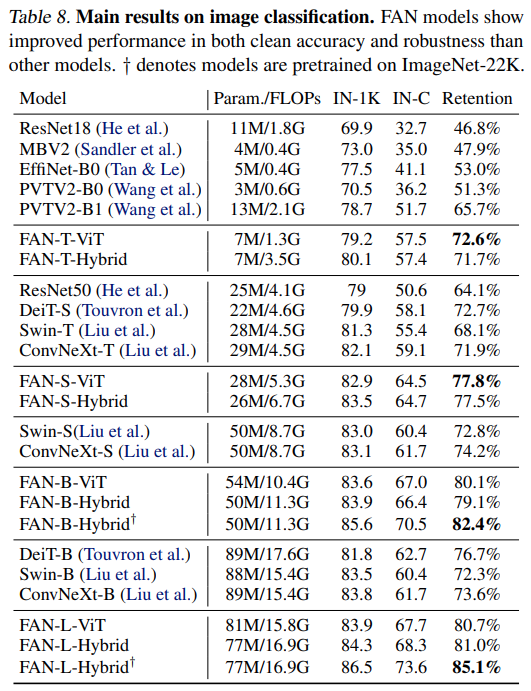
모델 크기에 따라 이미지 분류 성능을 정리하면 [표 8]과 같습니다. 모든 비교군에서 FAN 모델을 쓰면 큰 성능 향상이 있는 것을 볼 수 있습니다.

Robustness in semantic segmentation

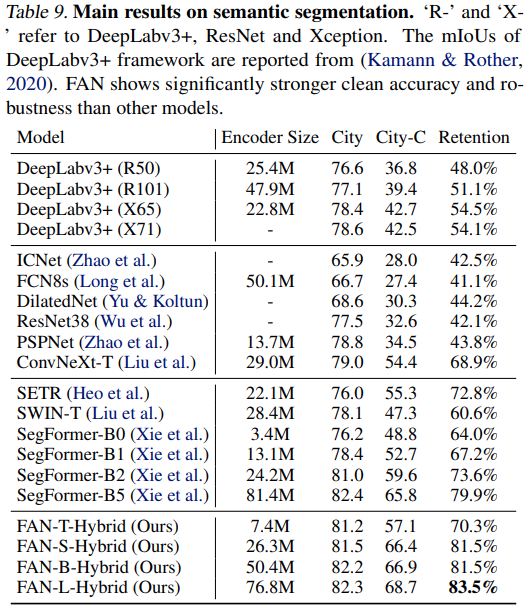
다양한 상황에서의 segmentation 성능 역시 좋은데요. City-C는 기존 Cityscape 데이터 셋에 16개의 자연적인 변형을 가한 데이터 셋입니다. (맨 위의 Introduction의 예시 그림 참고) 기존의 Segformer보다 훨씬 더 높은 Retention 성능을 보였다고 합니다.

Robustness in object detection

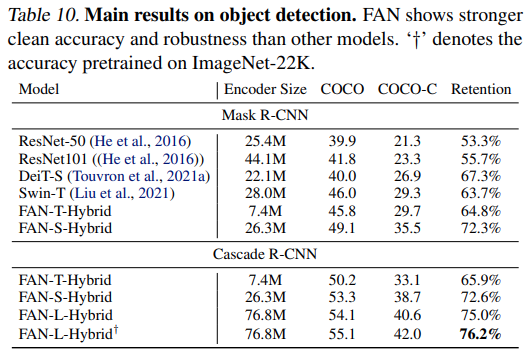
Detection에서도 사실 동일한 결과이고…

Robustness against out-of-distribution

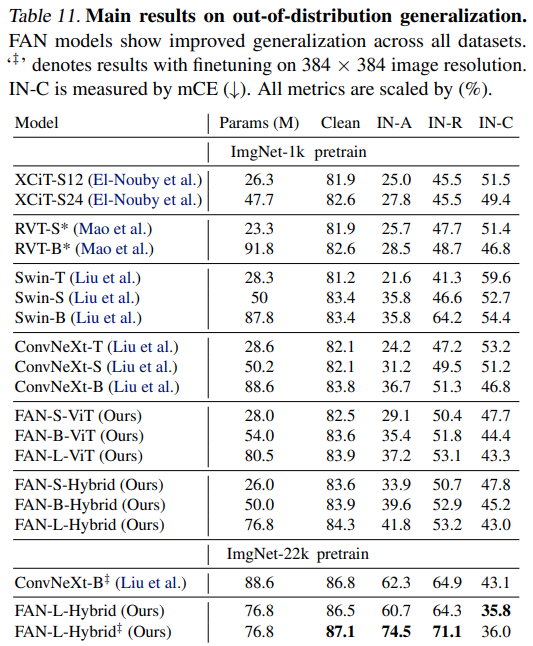
OOD 상황에서도 동일한 경향성을 보여줍니다.

Conclusion

사실 성능은 뭐… 좋으니까 제출했겠거니 싶기도 하고, 뒤쪽은 그냥 분석이 없고 성능만 쭉쭉 좋았다고 하고 넘어가서 저도 그냥 빠르게 넘어갔습니다. 핵심은 이 논문에서 Robustness를 향상시키기 위해 분석한 그 내용이 핵심이니까요~ 아무튼 첨보는 내용이 많아서 오랫만에 검색해가면서 잘 읽었습니다!