이번 리뷰 논문은 저번 리뷰에 이어서 비지도 학습 기반의 depth completion 논문을 들고 왔습니다. 해당 제목 그대로 기성 모델들을 teacher로 두고 distillation을 수행합니다. 다만, teacher 모델들의 출력값에 대한 에러를 이용하여 신뢰도에 대한 앙상블을 진행하는 positive congruent training 기법을 이용하여 학습을 진행합니다. 이를 통해 이전 방법론 안정적인 성능을 가질 수 있었다고 합니다.
Intro
해당 논문은 이전 리뷰에서 다룬 KBNet과 동일하게 단일 영상과 sparse point cloud 그리고 calibration K를 입력으로 dense depth map을 추론하는 방법을 사용합니다. 다만, 다른 특성을 보는 기존 모델(teacher) 특성들을 활용하여 더 높은 성능을 보이기 위해 knowledge distillation을 해당 태스크의 특성에 맞춘 방법을 소개합니다. 보다 구체적으로 설명하자면 다음과 같습니다. Depth map을 생성하는 기존 모델을 활용하기 위해, student 모델이 teacher의 error를 학습하지 않도록 하는 positive congruent training process를 생성하는 adaptive knowledge distillation을 제안합니다. 좋은 결과를 가진 모델 선별하거나 학습을 위한 GT가 없는 경우,Monitored Distillation라고 하는 이 방법을 사용하면 student model은 주어진 이미지의 reconstruction error를 가장 최소화하는 예측을 선택적으로 학습하여 teacher model들의 blind ensemble을 활용할 수 있습니다. Monitored Distillation는 특정 teacher model의 예측이 관찰된 이미지와 얼마나 잘 일치하는지에 대한 distilled depth map과 confidence map, 즉 ‘monitor’를 생성합니다. Monitor는 distilled depth에 적응적으로 가중치를 부여하는데, 모든 teacher가 high residuals를 보이는 경우에는 기존 unsupervised image reconstruction loss이 supervisory signal로 사용됩니다. 실내 환경(VOID)에서는 블라인드 앙상블 기준선 대비 17.53%, 비지도 방식 대비 24.25% 더 나은 성능을 보이며, 최고 성능의 지도 방식과 비슷한 성능을 유지하면서 79%의 모델 크기 감소를 보입니다. 실외(KITTI)의 경우, GT를 사용하지 않았음에도 불구하고 벤치마크 전체에서 공동 5위를 차지했습니다.
Method
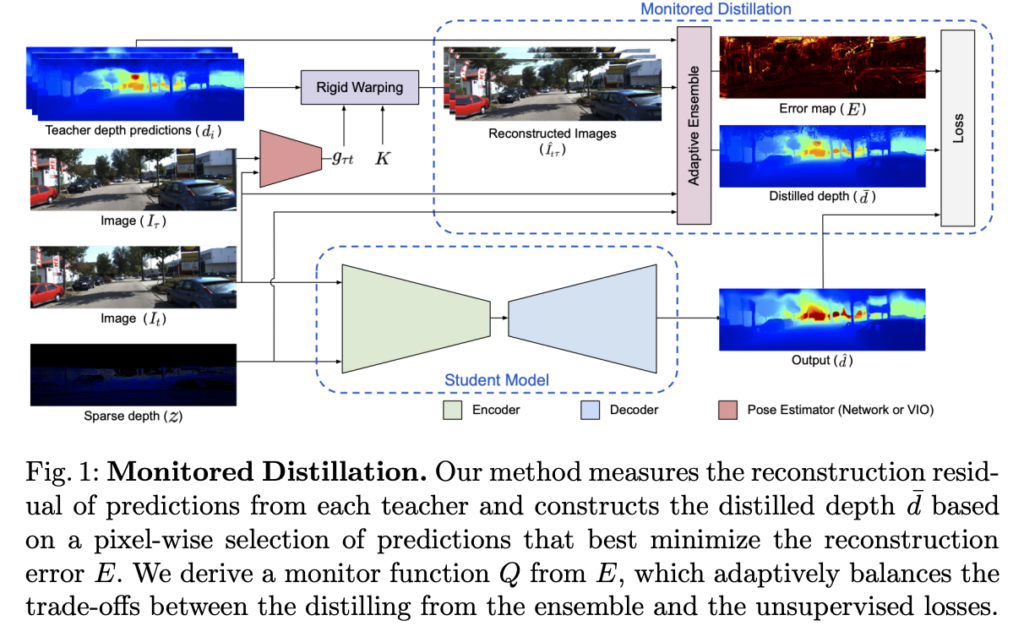
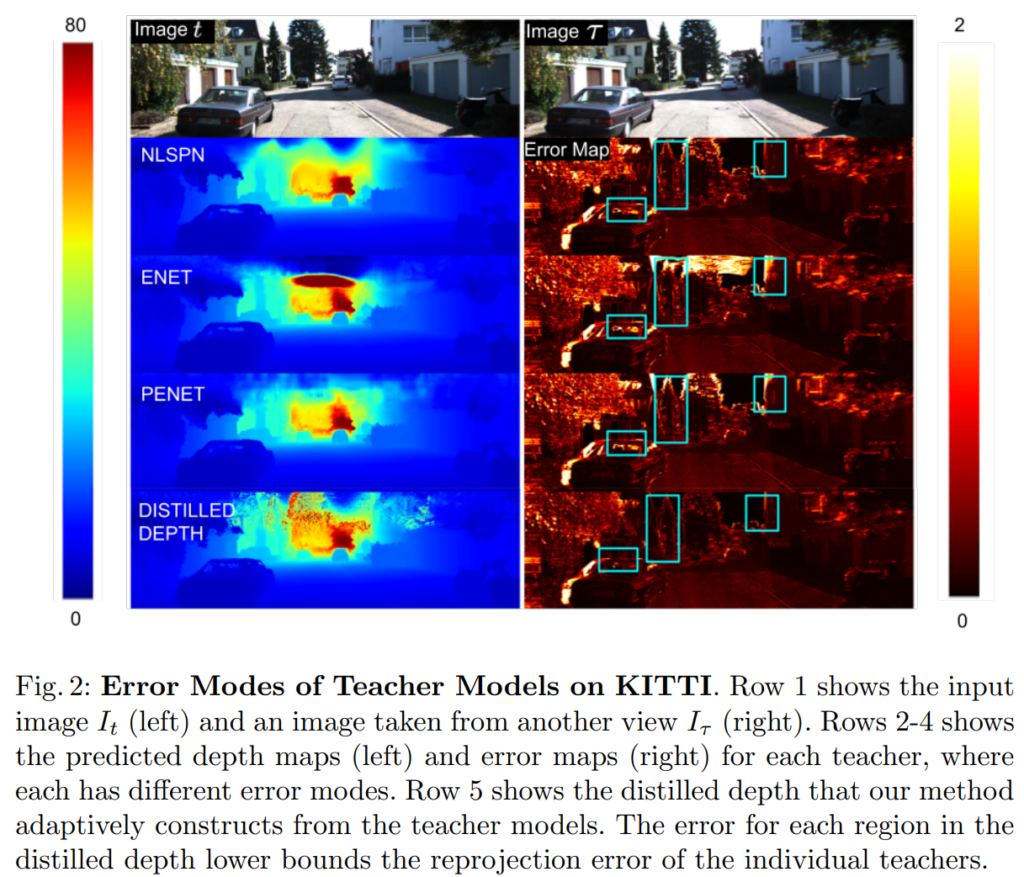
보정된 이미지 I와 이미지 평면에 투영된 sparse point cloud z에서 3차원 장면을 복구하는 것을 목표로 합니다. 이를 위해 I, z 그리고 카메라 고유 파라미터 k를 입력으로 받아 dense depth map d를 출력하는 함수 f_{\theta}를 학습하는 것을 제안합니다. 시점 t에서 촬영된 동기화된 영상과 sparse depth map \( I_t, z_t \) 의 각 쌍에 대해 공간적/시간적 인접한 시점 T의 영상 쌍을 이용할 수 있다고 가정합니다. 또한, M개의 모델 or “teachers” \{ h_i \}_{i=1}^M (e.g. 공개된 사전 학습 모델)을 이용할 수 있다고 가정합니다. fig 2에서는 각 teacher 마다 고유한 error mode가 존재함을 볼 수 있습니다. 이러한 특성을 활용하기 위해 모델을 선별하기 위한 모델의 성능을 평가할 수 있는 지표가 부족하다는 문제가 있습니다. 저자는 이 문제를 해결하기 위해 ensemble learning을 위한 adaptive knowledge distillation framework인 “Monitored Distillation”을 제안하여 결과적으로 positive congruent training 유도합니다. 즉, teacher 모델의 예측이 다른 뷰 시점과 어느 정도 일치하는 경우에만 학습에 사용하는 방식을 사용하는 것을 목표로 합니다. (~=positive congruent training)
이를 위해 I_t 와 I_{\tau} \in I_T 사이의 기하학적 제약을 활용하고, 각 교사가 생성한 예측값 d_i := h_i(I_t, z_t) 의 정확성을 검증하기 위해 서로 다른 뷰와의 photometric reprojection residuals에 대한 평균과 z와의 편차에 따라 가중치를 구합니다. 즉, 오차로부터 각 teacher 별로 현 시점 I_t 와의 호환성을 결정하는 confidence map을 정의합니다. 그런 다음 가장 높은 신뢰도를 산출하는 앙상블에서 픽셀 단위로 선택하여 distilled depth \bar{d} \ in \mathbb{R}_{+}^{H \times W} 를 구성합니다. 결과적으로 공간적으로 다양한 confidence map은 앙상블을 신뢰하는 것과 지도 학습 정보와 비지도 학습의 기하하적 일관성에 의존하는 사이의 균형을 맞추는 “monitor” 역할을 합니다.
Monitored Distillation.
주어진 M 개의 teachers와 teacher를 통해 추론된 depth map d_i, i \in \{ 1, ..., M \} 가 있을 때, 관찰된 point cloud와 영상간의 reconstruction error를 가장 최소하 하는 앙상블의 예측을 적응적으로 선택하여 distilled depth map [/latex] \bar{d} [/latex]를 구성합니다. 이를 위해 인접한 뷰 I_{\tau} 을 t 시점으로 재구성 합니다. 이는 다음과 같습니다.
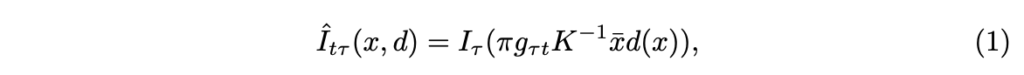
여기서 x 는 depth map의 한 값을 나타내고, x에 대한 homogeneous coordinate \bar{x} = \[x^{\top} \ 1 \]^{\top}를 나타냅니다. g_{\tau t} \in SE(3) 는 시점 t에 대한 상대적 카메라 포즈, K는 내부 카메라 파라미터를 나타냅니다. \pi 는 perspective projection을 의미합니다. g_{\tau t} 는 스테레오인 경우 camera baseline으로부터 도출하거나, Visual odometry를 통해 추론하거나, 비디오 뷰를 pose network를 통해 학습하여 추론하여 사용합니다.
각 teacher h_i 에 대해 I_t 과 재구성 영상 \hat{I}_{t\tau}(x, d_i), \tau \ in T 사이의 SSIM를 통해 photometric reprojection error P_i 를 측정합니다. 이는 아래와 같습니다.
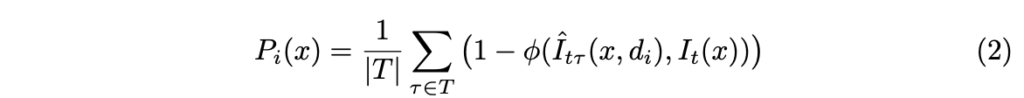
여기에서 표현을 편하게 하기 위해서 \phi() 를 SSIM 연산자로 노테이션 했다고 합니다.
Photometric reprojection을 단독으로 사용해서 scale 정보를 얻을 수 없기 때문에, \mathcal{N}(x) 로 표현되는 x의 근방인 k x k 만큼의 sparse point cloud에서 local deviation of teacher predictions를 추가로 측정합니다.
++ 알고 있는 sparse point를 지도 신호로 이용하여 측정하는 방식입니다.
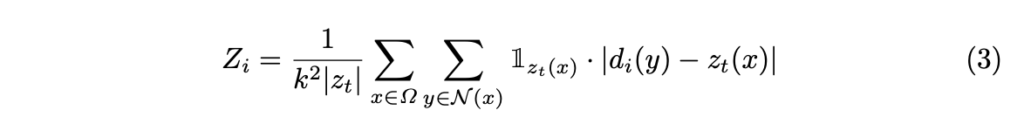
가중치로 사용되는 경우 \beta_i := 1 - exp(-\alpha Z_i) 는 서로 다른 teacher 간의 스메일 모호성을 해결하기 위한 역할로 상요됩니다. 여기서 α는 temperature parameter(~hyper parameter)에 해당합니다. 그런 다음 i번째 teacher의 가중치가 적용된 reconstruction residual E_i 를 다음과 같이 정의할 수 있습니다.
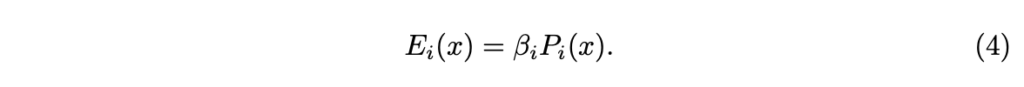
Distilled depth를 구성하기 위해 모든 teacher의 전체 residual error E_i 를 최소화하는 각 픽셀 x에 대한 깊이 예측 정보를 선택적으로 고릅니다.
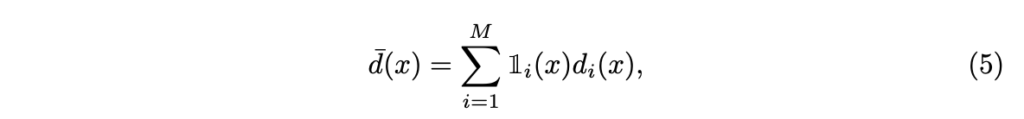
\mathbb{1}_i 는 i-th teacher에 대한 binary weight map으로 이는 다음과 같습니다.
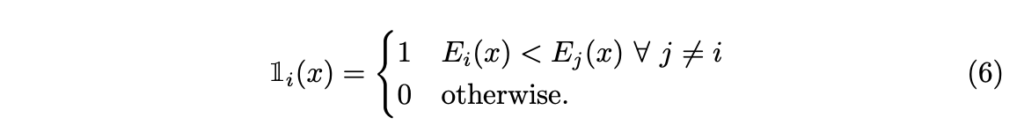
즉, d_i(x) 가 가장 낮은 photometric residual을 보일 때, \mathbb{1}_i = 1을 나타냅니다.
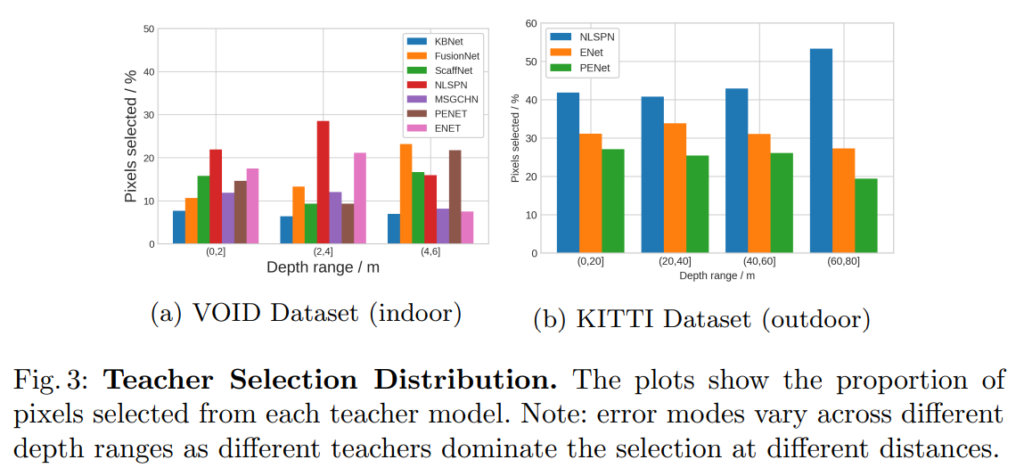
fig 1에서는 전반적인 파이프라인을 볼 수 있으며, fig 3에서는 distilled depth를 구성하기 위해 선택된 teacher에 대한 분포를 보여줍니다. 보이는 바와 같이 서로 다른 교사들은 서로 다른 depth range에 걸쳐 서로 다른 영역에서 좋은 성과를 보입니다. 저자는 제안한 방법을 통해 각 교사로부터 가장 낮은 오차를 가진 포인트~픽셀을 선택하여 adaptive ensemble을 생성할 수 있다고 합니다.
각 teacher model들은 GT를 이용하여 학습했음에도 불구하고 실제 depth range에 근사치를 구하기 때문에 reprojection residual를 기반으로 선택적으로 앙상블을 구성하는 방법을 구성하면 일부 error mode를 해결 할 수 있지만 모든 teacher가 높은 reprojection residual를 나타내는 경우가 발생할 수 있습니다. 그렇기에 저자는 앙상블을 완전히 신뢰하지 않고 error 대신에 distilled depth의 오차를 기반으로 monitor Q를 사용하여 적응적으로 가중치를 부여합니다. 각 교사에 대해 error map E_i 를 구성했기 때문에 픽셀에 따른 정보를 부여하기 쉽습니다. monitor map Q \in [0, 1]^{H \times W} 로 공간상 적응적으로 픽셀당 confidence map이며, 이는 아래와 같습니다.
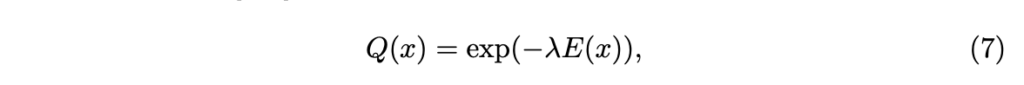
여기서 \lambda 는 temperature parameter에 해당합니다. Q는 자연스럽게 높은 신뢰도를 가진 distilled depth 맵에서 높은 점수를 가지게 됩니다. 이는 student model의 예측 값과 distilled depth 간의 지도 학습에 사용됩니다. 최종적인 monitored knowledge distillation loss는 아래와 같이 구성됩니다.
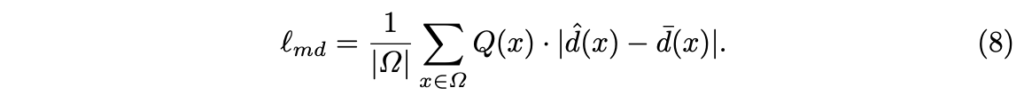
일반적으로 studnet model은 teacher model의 error도 학습하는 결과를 가져옵니다. 하지만 저자가 제안한 방법은 positive congruent~Q(x)을 이루는 teacher model의 예측 값들을 이용하여 적응적인 앙상블을 통해 증류를 수행하기 때문에 teacher model과 동일한 실수를 하지 않도록 학습을 진행합니다. 저자는 이를 Monitored Distillation라고 정의하며 monitor function Q는 재구성 오류가 낮은 영역에 있는 교사에게 더 높은 가중치를 부여합니다. 앙상블 내의 모든 교사가 높은 잔차를 예측하는 경우에는 모든 교사의 일반적은 오류를 학습하지 않도록 비지도 학습 기바느이 손실 함수로 대체하여 학습을 진행합니다.
Unsupervised Objective.
앞에서 언급한 바와 같이 Q를 이용하여 높은 reconstruction error이 발생한 경우에는 비지도 학습 기반의 손실 함수를 이용한 학습을 진행합니다. 해당 태스크에서는 일반적으로 unsupervised photometric reprojection error (i.e. color and structural consistencies)를 이용합니다. 이는 아래와 같습니다.
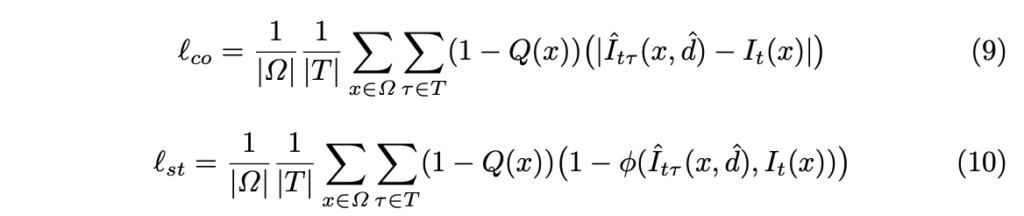
적용하는 방법은 아주 간단합니다. adaptive monitor function (1−Q)를 통해 신뢰도가 떨어지는 영역에 대해서는 비지도 학습 신호를 전달합니다. 즉, 한번 더 정리하면 앙상블의 신뢰도가 높은 경우에는 l_{md} 를 사용하고 신뢰도가 떨어지는 경우에는 비지도 학습 신호를 사용하여 학습을 진행합니다.
하지만 각 정보들의 부자연스러운 현상을 나타낼 수 있기 때문에 local smoothness regularizer을 이용하여 평탄화를 수행합니다.
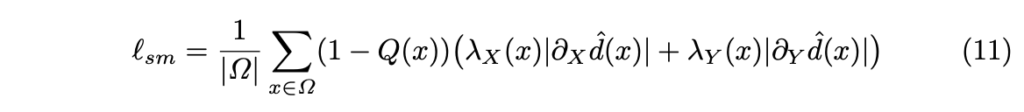
여기서 \partial_X, \partial_Y 는 x와 y 방향에 대한 미분, 가중치 \lambda_X := e^{- \| \partial_X I_t(x)\|} ~ \lambda_Y := e^{- \| \partial_Y I_t(y)\|} 에 해당합니다.
따라서 전체적인 loss는 아래와 같이 정의 할 수 있습니다.
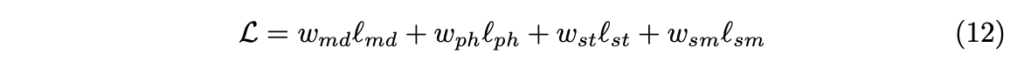
Experiment
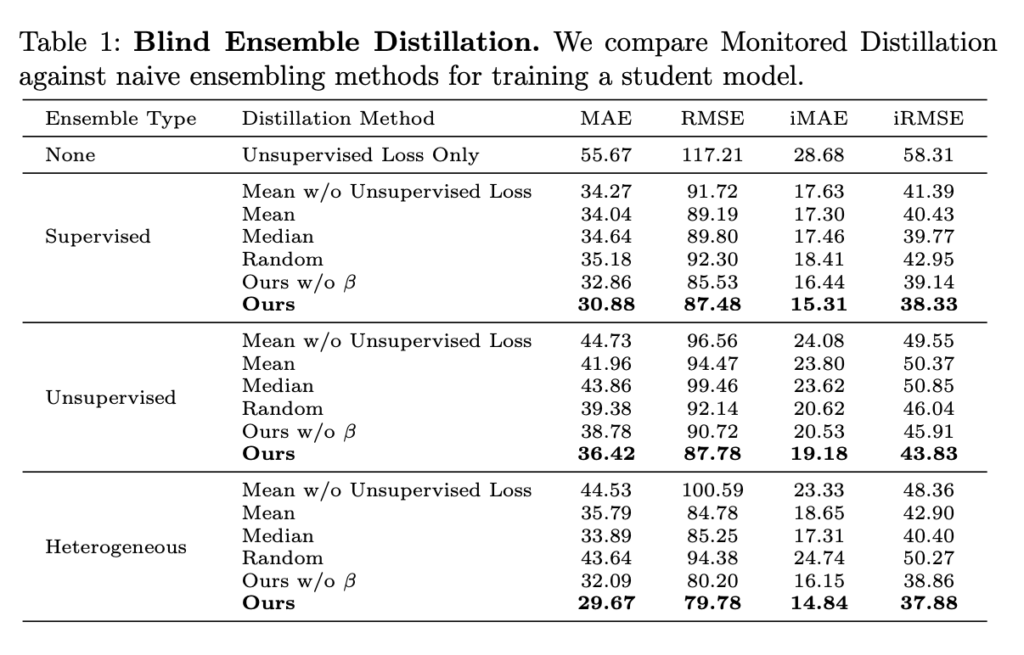
Tab 1에서는 해당 블라인드 앙상블 기법의 범용성을 입증하기 위해 지도학습/비지도/Heterogeneous 기반의 teacher 모델을 이용하여 수행한 결과를 보이며, 어느 방법에서도 높은 결과를 보여줍니다. 또한 나이브한 앙상블 기법 mean/median/random을 이용한 결과 대비 높은 결과를 보여줍니다. 또한 scale 정보가 부여된 β를 사용한 경우에 MAE 기준 2~3 성능 향상을 보여줍니다.
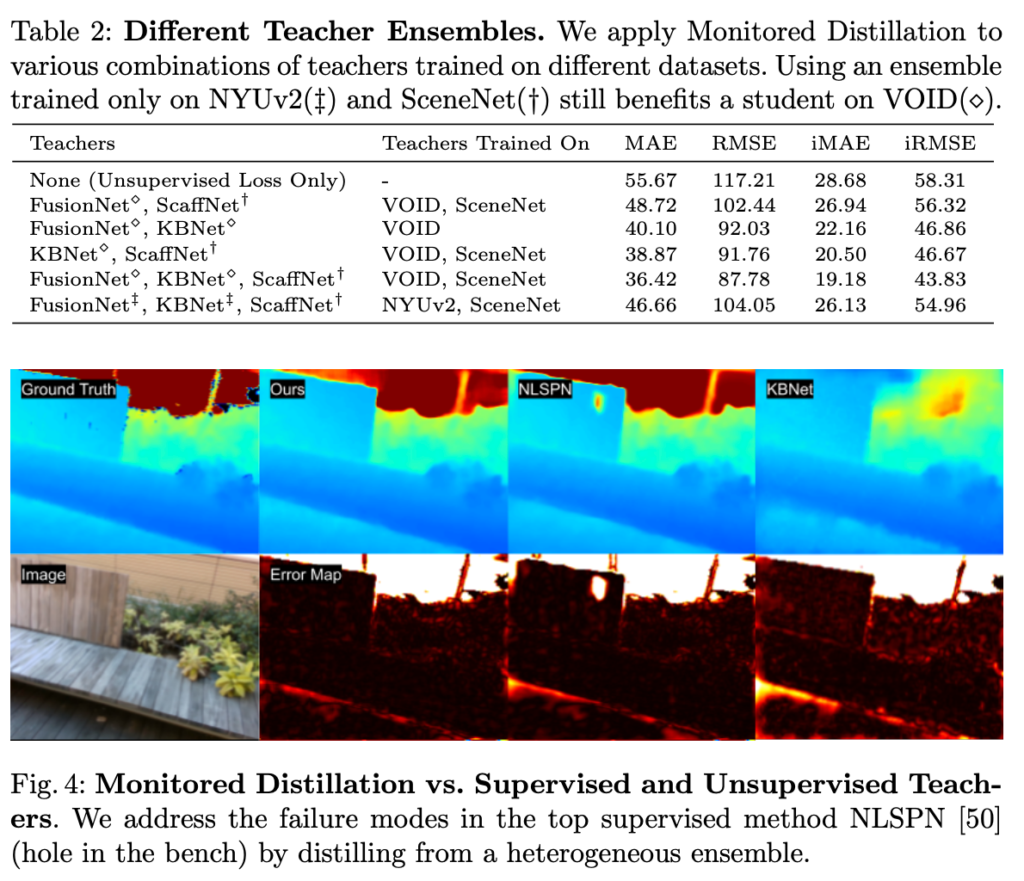
Tab 2에서는 teacher model/학습 데이터 등 조합에 따른 성능 비교를 보여줍니다.
Fig 4에서는 정성적인 결과를 통해 타 방법론 대비 성능 향상을 보여주고 있습니다.
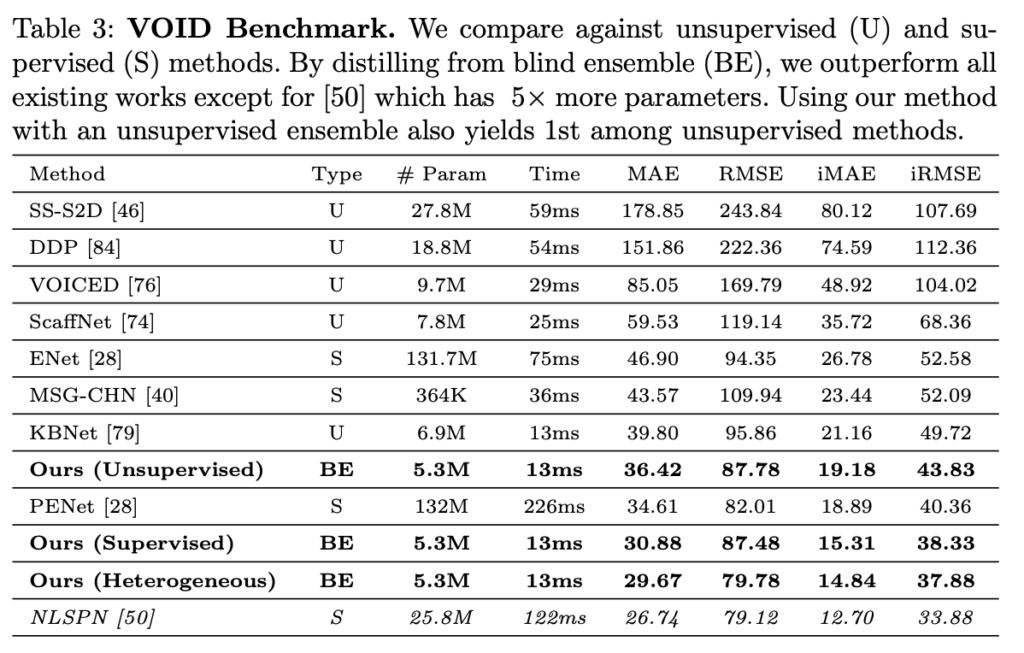
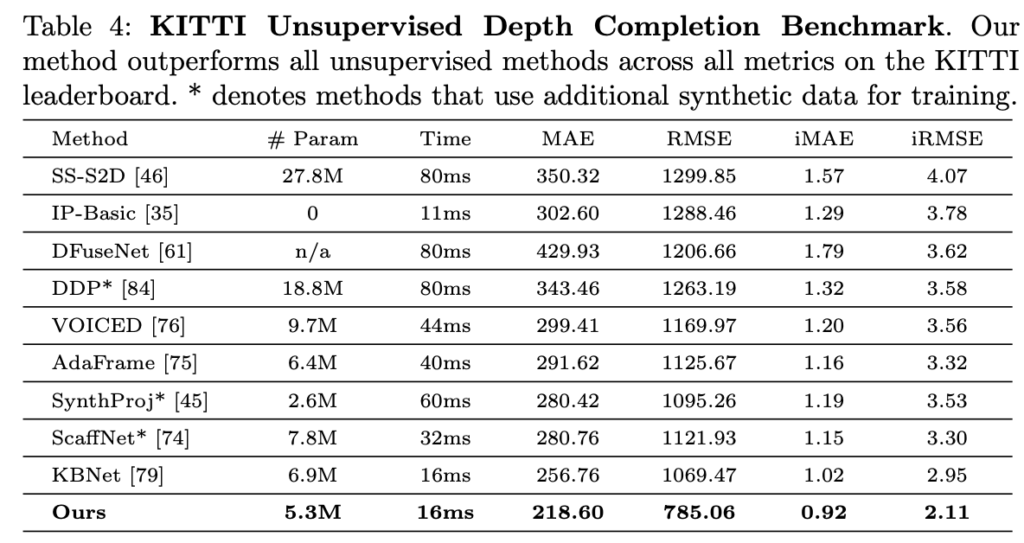
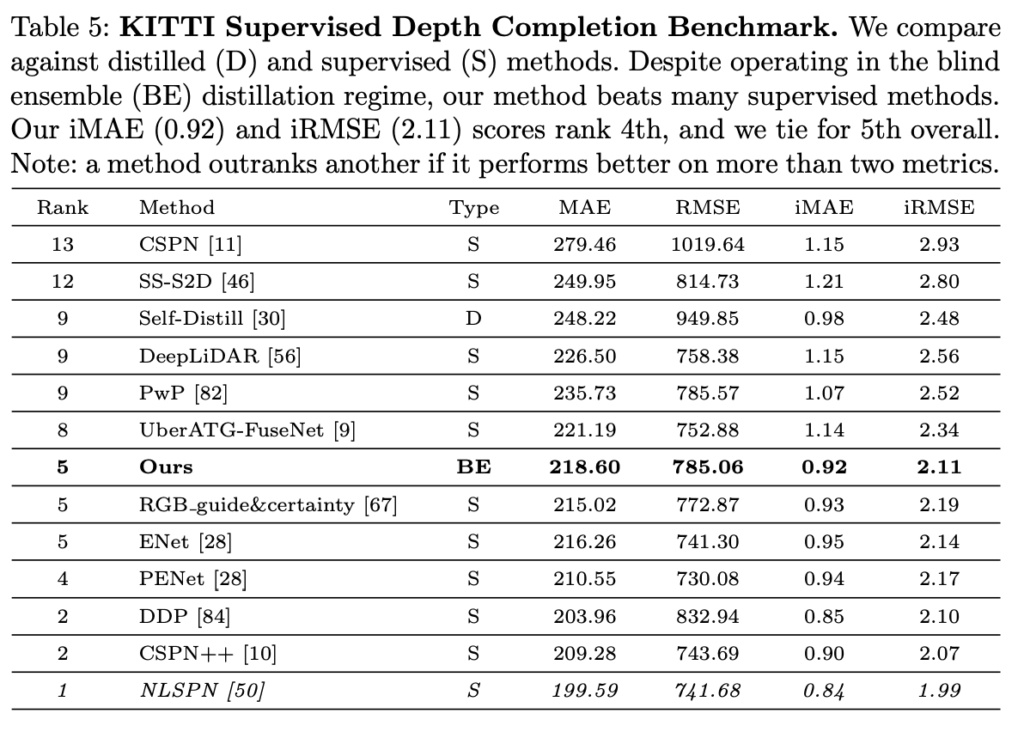
Tab 3-5에서는 Depth completion 태스크에서 가장 알려진 VOID, KITTI에서 성능 평가를 보였고, 표와 같이 지도 학습와 비교 했을 때도 좋은 결과를 보여주고 있습니다.