이번에 리뷰로 작성할 논문은 CVPR 2021에 게재된 Depth Completion 관련 논문입니다. 사실 이번 주 초청세미나에서 발표를 해주신 이병욱 박사님의 논문이기도 합니다. 세미나 때 들었던 컨셉이 흥미로워보여서 논문으로 읽고 리뷰를 작성하게 되었습니다.
Intro
일단 Depth Completion이라는 task는 Dense하면서도 정확한 깊이 정보를 추출하고자 하는 task입니다. 여기서 정확한 Depth는 Lidar와 같이 거리를 측정할 수 있는 센서값을 활용할 수 있겠으나, Lidar는 Dense한 Depth 정보를 취득할 수 없습니다. 반면에 RGB 영상은 Dense한 정보를 가지고 있기는 하지만 거리를 측정하려면 기하학적인 기법 혹은 딥러닝 모델이 필요하며, 추정된 깊이 마저도 부정확하게 됩니다.
따라서 Depth Completion이라는 taks는 sparse한 depth information과 Dense한 RGB 정보를 잘 조합하여 Dense하면서도 정확한 깊이 맵을 추정하는 것을 목표로 합니다. 그리고 해당 task는 CNN 기반의 딥러닝 모델에 Sparse depth와 RGB input을 입력으로 주어서 학습 및 추론을 진행합니다.
초기에 Depth Completion 방법론은 regression 방식으로 모델이 예측하고 이를 학습했기 때문에, object boundary와 같은 정보들을 유지하는 것이 매우 어려웠다고 합니다. 이러한 문제점을 해결하고자 입력 RGB 영상으로부터 추출된 정보를 최대화하여 초기 regression output depth 값을 조정하고자 하였습니다.(아마 context 정보 등을 보완하고자 한 것 같네요.)
또 다른 방법론으로는 depth map으로부터 surface normal과 같은 추가적인 정보를 추출하여 학습단계에서 기하학적 가이드를 제공하는 방식을 택했다고 합니다. 이러한 방법론들은 우수한 성능을 보여주었지만, 여전히 edge information 등을 보충해주기에는 부족했으며, 추가적 정보를 추출하기 위한 추가 네트워크로 인하여 추가적인 컴퓨팅 파워(메모리, 시간)가 많이 들었다고 합니다.
따라서 본 논문에서는 컴퓨팅파워는 최소화하면서 모델이 효과적으로 Depth Completion을 수행할 수 있도록 하는 새로운 학습 framework을 제안합니다. 가장 먼저 Plane-Residual(PR) representation이라는 것을 제안하는데, PR representation이란 absolute depth를 2개의 paratmer (p, r)로 표현하는 것을 의미합니다.
여기서 p는 사전 정의된 이산적인 깊이 평면들 중 어느 평면에 속하는지를 나타내는 값을 의미하며, r은 p를 통해 선택된 평면을 기준으로 얼만큼 더 움직여야하는지를 나타내는 normalized distance를 의미합니다.
이러한 PR Representation을 통해서 일반적으로 Depth Completion method들이 많이들 활용하는 direct regression problem 문제를 depth plane classification과 plane 사이에 residual regression 문제로 바꾸어서 풀 수 있게 된다고 설명합니다. 사실 이 PR Representation이 해당 논문의 거의 전부라서 어떻게 PR Representation을 통하여 Depth Completion network를 학습시켰는지가 매우 중요할 것 같습니다.
Method
그럼 방법론에 대해서 알아보도록 하겠습니다. 먼저 PR Representation에 대한 보다 자세한 정의에 대해서 살펴보죠. PR Representation의 가정은 우선 카메라의 전방에 평행한 평면들이 depth 축에 따라 일정 간격으로 존재한다고 가정합니다.
이를 수식으로 표현하면 d_{p \in [1,2,...,D]}로 볼 수 있으며 여기서 1에 해당하는 값은 카메라와 가장 가까운 평면을, D는 카메라로부터 가장 멀리 떨어진 평면이라고 볼 수 있게 됩니다. 이러한 depth image 안에서, 각각의 픽셀값은 총 2개 (p, r)로 표현을 할 수 있으며, 여기서 p는 몇번째 depth plane에 속해있는지를 의미하는 classification을, r은 해당 평면을 기준으로 얼만큼 더 움직여야하는지 잔차를 의미하는 regression 값을 의미합니다.
이 r값의 경우에는 -0.5~0.5 사이의 범위 값을 가지고 있으며, 제일 첫번째 평면의 경우에는 0~0.5의 값을 가지고 있습니다. 즉 3번째 depth 평면에 속하면서 4번째 depth 평면 방향으로 0.3만큼 움직인다면 픽셀값은 (3, 0.3)이 되는 것이죠.
이러한 plane depth와 regression depth가 주어졌을 때, absolute depth value는 아래 수식과 같이 표현됩니다.
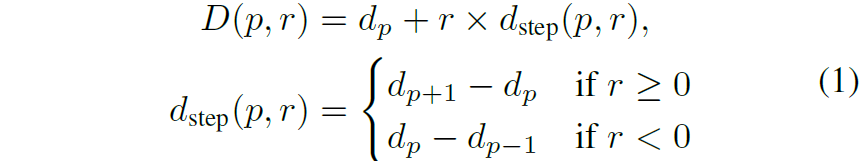
여기서 d_{p} 는 depth plane의 값을, d_{step} 는 scale이 반영된 실제 depth value로 풀이됩니다. 수식이 어렵게 느껴지시면 아래 그림을 참고하시면 더 좋을 듯 합니다.
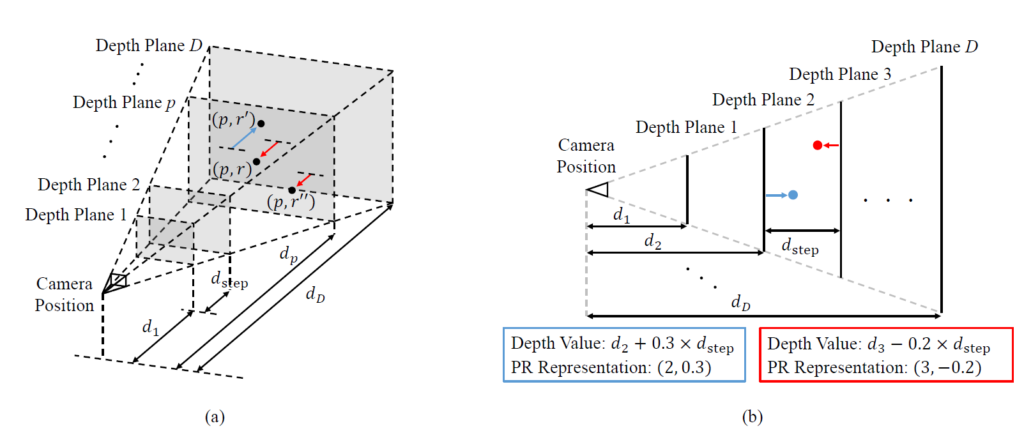
Network Design
그럼 전반적인 모델 아키텍쳐에 대해서도 알아보도록 하죠. 모델의 전체 framework은 그림2와 같습니다,.
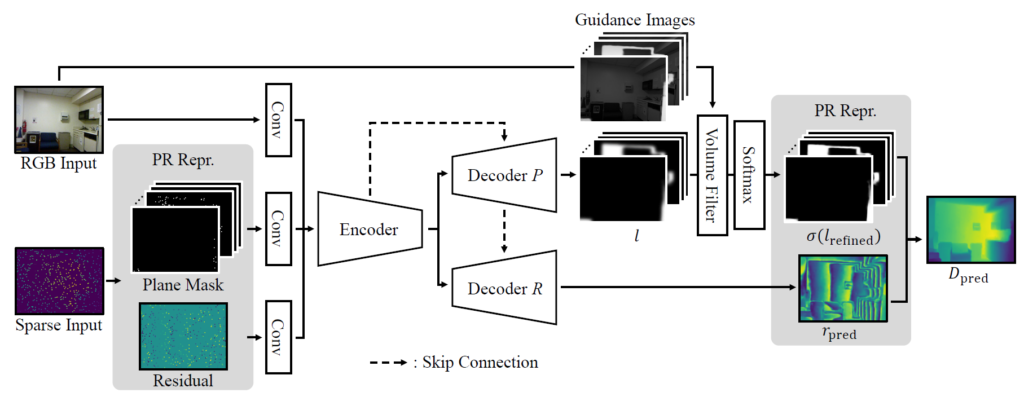
먼저 입력으로는 RGB 이미지와 Sparse Depth input이 들어오게 됩니다. 여기서 Sparse Input은 PR Representation으로 구분되어 Depth plane과 Residual map으로 표현이 되게 됩니다. 이러한 multi-modality 입력에 대하여 Encoder는 하나의 ResNet을 통해서 구현이 되어 있으며, 다만 Decoder 부분에서 Depth Plane과 Residual map을 따로 계산할 수 있도록 2가지 네트워크로 구분을 둡니다.
한가지 재밌는 점은, Plane Decoder에 경우에는 Encoder의 feature map으로 long-skip connection을 수행하지만, Residual Decoder의 경우에는 Plane Decoder의 feature map을 활용해서 skip-connection이 이루어진다는 점입니다. 저자는 결국 Residual map 자체는 Depth plane을 기준으로 결정이 되는 것이다보니 둘의 연관성이 깊어 Encoder feature map이 아닌 Plane Decoder의 값으로 skip-connection을 진행하였다고 합니다.
또한 input domain에서의 feature map도 결국 depth 정보가 포함되어있기 때문에 long-skip connection을 수행할 때 concatenation보다는 summation으로 진행이 되었다고 하네요.
위에서 설명드린 내용에 대한 보다 자세한 그림은 아래 그림과 같습니다.
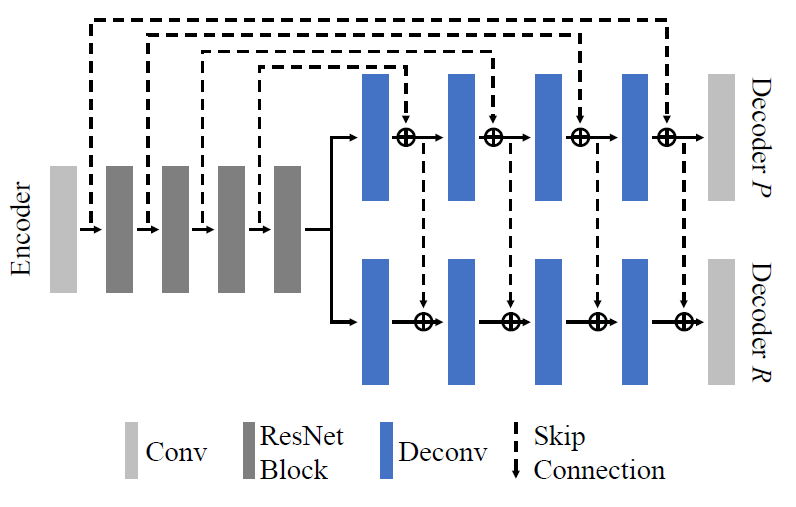
그럼 Decoder들이 추론하는 output 값에 대해서 조금 더 자세히 알아보겠습니다. Decoder P는 D 채널 축에 softmax를 적용하여 확률 분포를 값을 추론합니다. 그리고 Decoder R의 경우에는 1개의 단일 채널의 normalized residual map을 추론하게 됩니다. 이렇게 각각의 디코더에서 나온 추론 값을 통해 최종 depth map을 만드는 과정은 아래 수식과 같습니다.
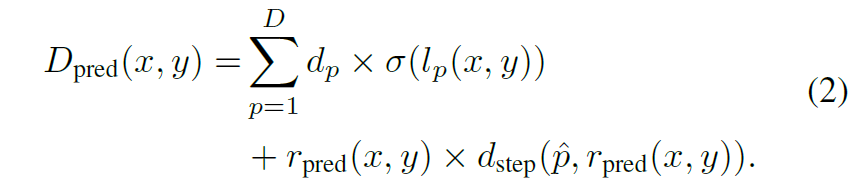
여기서 sigma 값은 softmax function을 의미하며, l_{p}는 depth plane p에 대한 raw classification 값을 의미합니다. \hat{p}는 softmax를 취해서 나온 가장 확률값이 높은 class(즉 plane)의 값을 의미합니다.
수식1과 다르게, 저자들은 최종 depth를 계산할 때 확률볼륨( \sigma(l_{p}))의 가중합을 사용했다고 합니다. 이러한 가중합 방식은 서로 다른 depth plane이 만나는 지점(예를 들어, 전경의 객체와 배경이 마주하는 가장자리 영역)에 대하여 depth 결과를 추론할 때 보다 부드러운 결과를 만들어줄 수 있다고 합니다.
Probability Volume Filtering
해당 부분은 depth plane classification의 성능을 끌어올리기 위해, channel-wise guided image filtering 기법을 적용한 것을 의미합니다. Guided image filtering이란 guidance image로부터 content 정보를 추출 및 활용하여 edge들이 잘 보존되도록 하는 기법을 의미합니다.
이러한 테크닉들은 stereo matching task에서 두 영상 사이에 대응되는 매칭들을 나타내는 cost volume의 각 채널 축에다가 적용하였을 때 매우 효과적이었는데, 저자가 제안하는 Depth plane 방식 역시도 어떻게보면 cost volume과 유사한 구조로 볼 수 있기에 이러한 guidance technique을 쉽게 적용할 수 있었다고 합니다.
이러한 guide를 주기 위하여, 저자는 RGB input image를 2개의 연속된 컨볼루션 레이어에 적용하여 D 채널의 가이드 이미지를 만들었다고 합니다. 이러한 가이드 이미지들은 초기 depth plane에 채널축에 대한 guide를 아래 수식과 같이 수행합니다.
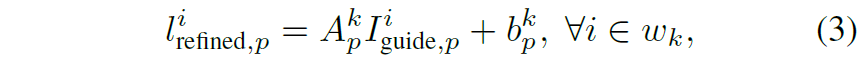
p, w_{k} 는 각각 pixel location과 픽셀 k를 중심으로 하는 윈도우를 의미합니다. A^{k}_{p}, b^{k}_{p} 는 각각 I_{guided,p}, l_{p}, w_{k}의 평균, 분산, 공분산을 통해 결정이 된다고 하며, 이러한 연산을ㄴ 위해 average pooling 과정을 적용했다고 합니다.
따라서, image guiding 방식을 통해 refine된 최종 depth map은 아래와 같습니다.
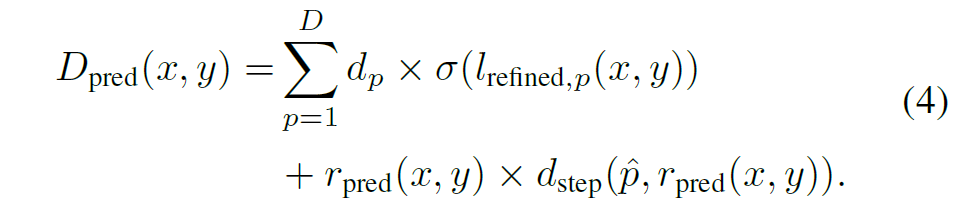
Confidence based Regression
해당 부분은 residual regression을 수행하는 decoder R에 대한 loss function을 의미합니다. 반복해서 설명드렸다시피 PR Representation에서는 Depth를 추론할 때 depth plane과 해당 plane에서의 residual regression을 통해 계산이 된다고 하였습니다.
여기서 Regression을 수행하는 decoder를 학습시킬 때 아무리 올바른 regression을 계산하였다 하더라도, 애초에 depth plane이 잘못 예측이 된다면 매우 부정확한 depth가 만들어지는 문제가 발생합니다. 따라서 저자는 decoder R를 학습시킬 때 학습에 사용되는 loss의 가중치를 depth plane classification의 confidence에 맞추어 주는 방식을 채택했다고 합니다.
보다 구체적으로, decoder R을 최적화할 때 GT depth map과 GT residual map( r_[gt}) 사이에서 얼만큼에 가중치를 더 둘것인지를 plane의 confidence score를 보고 결정하게끔 한다고 합니다. 해당 confidence score를 계산하는 과정은, 각 픽셀의 확률 볼륨( \sigma(l)들의 채널 별 최대값을 통해서 가져올 수 있었다고 합니다.
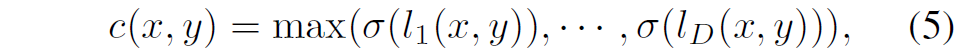
각 픽셀별로, 높은 depth plane confidence score를 가지고 있다면, GT residual value에 대하여 더 많은 supervision을 받을 수 있도록 할 것이며, 반대로 작은 depth plane confidence score를 가지는 픽셀들의 경우에는 residual value보다는 Depth GT에 대한 guide를 더 많이 받도록 loss를 설계하는 것입니다.
실제로 학습 초기에는 Decoder R과 P가 모두 부정확하기 때문에 Depth GT에 대한 supervision을 더 많이 받으며, 학습이 점차 진행되어 Decoder P의 정확도가 어느정도 올라가게 될 경우에는 Decoder R의 residual 쪽에 더 많은 가중치가 쏠려서 학습이 진행된다고 합니다.
Loss Function
Loss term은 크게 1)Final Loss , 2) Depth Plane Classification Loss, 3) Residual Loss 와 같이 3가지로 구성되어 있습니다. 1번의 경우는 아래 수식과 같습니다.
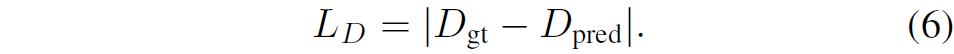
2번의 경우에는 classification이기 때문에 Cross-Entropy Loss와 같이 구성이 되어 있습니다.
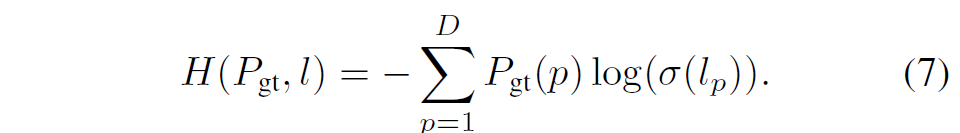
다만 한가지 신경쓸 점은, Depth Plane이 초기 initial 버전이 하나 있고, image guiding을 통해 refined 버전이 하나 있는데 이 초기 버전과 refine 버전 모두에게 수식 7번의 loss를 적용한다고 합니다.
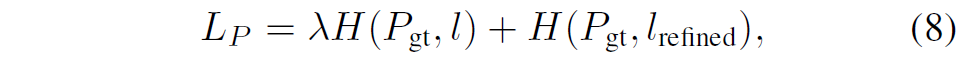
마지막으로 residual loss는 아래 수식과 같이 정의할 수 있습니다.
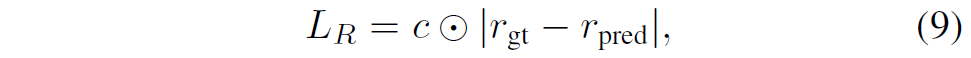
여기서 c값은 이전 서브섹션에서 설명드린 Confidence score를 의미합니다.
Experiments
다음은 실험 섹션입니다. 학습 및 평가는 실내 상황인 NYU Depth v2 데이터 셋과 실외 상황인 KITTI Depth Completion Dataset으로 구성이 되어있습니다. 실내 환경은 비교적 최대 거리가 짧기 때문에 Depth plane을 8개로 결정하였으며, 반대로 KITTI와 같은 outdoor 환경에서는 Depth Plane을 64개로 설정하였다고 합니다.
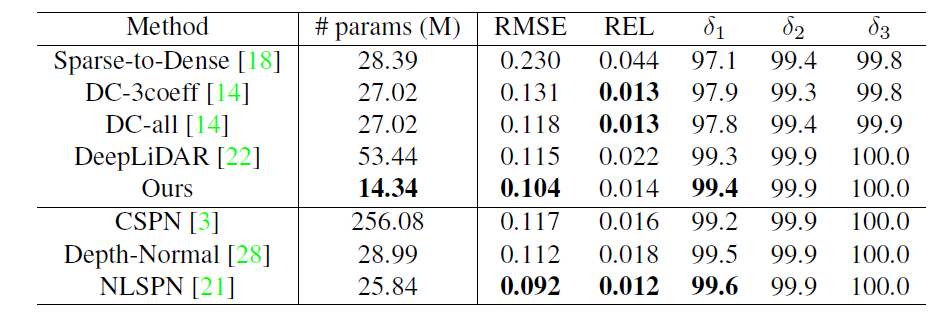
위에 표는 NYU-V2 데이터 셋에 대한 정량적 비교 결과 표입니다. 위에 5개의 방법론은 후처리를 통한 refinement 방법론이 포함되지 않음을 의미하며, 아래 3개의 방법론은 후처리 보정 과정이 포함된 방법론이라고 합니다.
제안하는 방법론이 파라미터 수가 가장 적음에도 불구하고, RMSE 성능이 가장 좋을 것을 볼 수 있으며, REL 성능에서는 0.001로 매우 근소한 차이를 보여주고 있습니다. 그리고 아래 후처리 방법론들의 경우에도 NLSPN을 제외하고는 더 적은 파라미터 양과 성능을 보여주고 있네요.
DC-3coeff, DC-all 방법론들은 모두 classification 기반의 방법론으로 80개의 depth plane을 추론한다고 합니다. 그 후 DC-all은 80개에 대한 weighted sum으로 최종적인 depth를 추론하고, DC-3coeff는 가장 확률 값이 높은 3개의 값에 대한 가중합을 수행한다고 합니다. 이러한 classification 방식은 REL 메트릭에 대해서는 더 좋은 성능을 보여준다고 합니다.(왜 그런지에 대해서는 구체적으로 언급이 없네요. 논문의 표현 방식도 believe라고 하는 것을 보아 추측성으로 보입니다.)
다만, 보다 더 정확한 성능을 보여주기 위해서는 depth plane의 수가 충분히 존재해야만 한다고 합니다. 반면에 제안하는 방법론은 Regression module이 따로 존재하기 때문에 depth plane의 수가 8개만 있어도 충분한 성능을 달성할 수 있으며 REL 말고도 다른 metric에서 긍정적인 성능을 보였다고 합니다.

정성적 그림에서도 보시면 제안하는 방법론이 책상등과 같은 대상을 잘 추론하였으며 특히 object boundary가 선명하다고 주장합니다. 이는 Depth Plane을 분류하는 방식을 통해 객체의 경계면에서 depth 값들이 mixing되는 현상이 많이 완화되었기 때문이라고 하며, depth plane으로부터 residual 값을 잘 regression하여 보다 디테일한 정보들을 잘 표현할 수 있었다고 합니다.
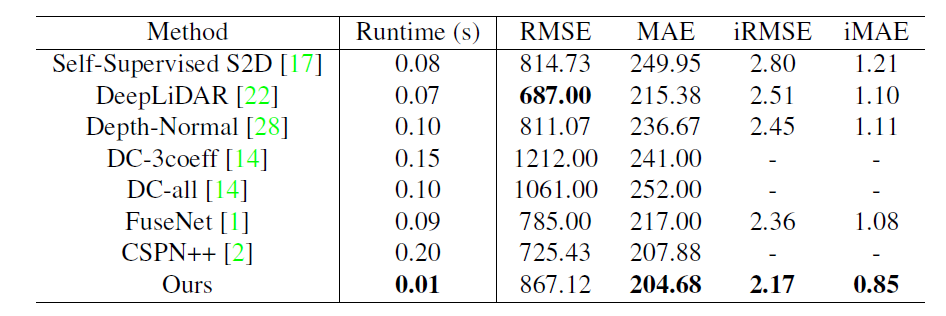
다음은 KITTI 데이터 셋에 대한 결과입니다. 해당 실험에서는 runtime을 함께 보여주는데 0.01초 즉 100FPS의 매우 빠른 속도를 보여주면서도 MAE와 iRMSE에서는 가장 좋은 성능을 보여주고 있습니다.
Ablation study
다음은 ablation study에 대한 실험입니다. 실험 가짓수로는 크게 4가지로, 첫째는 depth plane을 어떻게 정의할 것인지, 둘째는 Depth plane의 개수를 몇으로 지정할 것인지, 셋째는 Filtering 과정을 적용할 것인지, 마지막으로 Regression loss를 적용할 때, Confidence-guiding을 적용할 것인지에 대한 결과입니다.
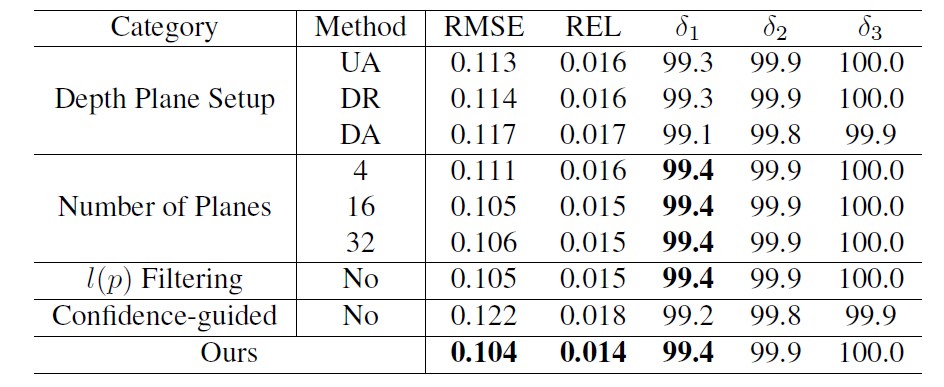
먼저 첫번째 실험부터 보시죠. Depth Plane Setup에서 가짓수가 크게 3가지로 UA, DR, DA가 존재합니다. 각각은 다음과 같습니다.
- UA: Uniformly & Absolutely
- DR: Disparity-wise & Relatively
- DA: Disparity-wise & Absolutely
위 경우에 대하여 예를 들면, 초기 시작 depth 값을 0m로 잡고 가장 마지막 depth plane의 값을 10m로 설정하는 경우 0~10미터 사이에 대해 일정한 간격으로 depth plane들을 설정하는 것이 UA 세팅입니다.
그리고 DR과 DA의 경우에는 이전의 연구들이 depth plane을 uniform하게 두지 말고, Disparity map 혹은 log-scale로 변환하는 것이 더 좋은 성능을 보여준다고 하였던 세팅입니다. 저자는 이러한 3가지 세팅에 대하여 실험을 해보았으며 결과적으로 이전 방법론들의 주장과 달리 Uniform하게 설정하는 것이 가장 좋았다고 합니다.
이러한 실험 결과에 대하여 기존의 방법론들은 최종적으로 가장 최적의 depth plane을 찾아야하는 것이 목표였지만, 제안하는 방법론의 경우 classification 결과로부터 residual depth를 계산해야하는 PR Representation 방식이기 때문에, 보다 residual을 잘 구하기 위해서는 항상 일정한 depth plane을 가지는 것이 더 좋았다는 설명입니다.
두번째 실험으로는, Depth plane의 개수에 대한 실험인데, 일단 8개일 경우가 가장 좋았으며, 16, 32인 경우에도 4보다는 더 좋았다고 합니다. 하지만 직관적으로 depth plane의 개수가 더 많아질수록, classification task가 더 어려워지며(예측해야할 값이 많아지다 보니), sparse depth가 input으로 사용이 되다 보니, plane classification을 학습시키는 것 역시 더 어렵다고 합니다. 따라서 classification task의 부담을 덜어주고자 8개의 값을 적용했다고 하네요.
다음으로는 probability volume filtering 관련 ablation 실험입니다. 비록 image guding을 통한 volume filtering이 성능을 막 드라마틱하게 끌어올리는 것은 아니지만, 그림5의 정성적 결과에서 보시다시피 가이딩을 하게 될 경우 얇고 가는 객체에 대해서도 선명하게 depth를 추론할 수 있다고 합니다.
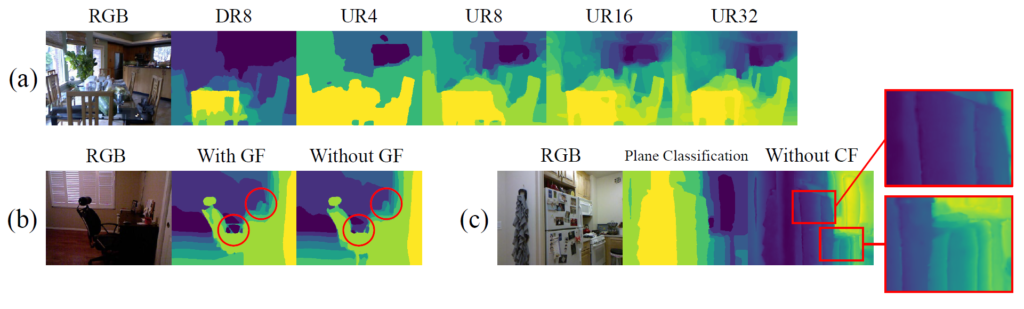
마지막으로 Confidence guided residual regression에 대한 실험입니다. 해당 regularization이 없게 될 경우 성능이 매우 드라마틱하게 감소하는 것을 볼 수 있습니다. 실제로 그림5의 c를 살펴보시면 CF가 없을 경우 depth plane의 경계면에서 원활하게 regression을 구하지 못해 부드럽지 못하고 어색한 boundary가 발생하는 것을 볼 수 있습니다.
결론
컨셉이 참신하고 좋아서 재밌게 읽은 논문이네요.
리뷰 잘 읽었습니다.
본 논문에서 수행하는 depth completion과 제가 아는 depth estimation이 결국 서로 다른 task 인건가요? 아니면 유사하거나 같은 건가요??
리뷰 초반부에서 depth completion task에 대한 설명을 해 주실 때 ‘ Dense하면서도 정확한 깊이 정보를 추출하고자 하는 task’ 라고 언급을 해 주셨는데, 이건 사실 monodepth, transdssl 등과 같은 depth estimation 도 동일한 것이지 않나요.?
그리고 RGB 이미지와 함께 모델의 input 으로 들어가는 sparse input 이라는 것이 그냥 lidar point 인 것이죠???
감사합니다!