[ICCV2021](Oral) Motion Basis Learning for Unsupervised Homography Estimation with Subspace Projection

이번에 소개할 논문은 21년도 ICCV oral paper로 게재된 논문으로, 비지도학습 방식의 호모그래피 추정 방법론을 새롭게 제안합니다.

Preliminary

호모그래피는 다들 아시다시피 2D plane과 2D plane 사이에 변환 관계를 나타내는 행렬입니다. 여기서 이 변환 관계에는 Rotation, Translation, Similarity, Affine, Perspective Projection 등 다양한 경우들이 존재로 하는데, 2D plane에서 표현할 수 있는 거의 모든 변환 상황들을 담고 있는 것이 이 Homography matrix(혹은 Perspective Matrix)라고 합니다.

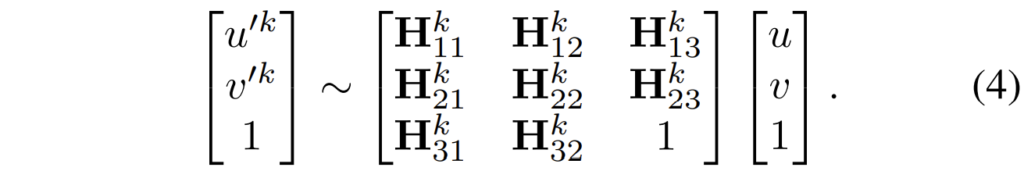
이러한 두 평면 간에 관계를 계산하기 위해서는 두 평면 사이에 대응점이 일정 개수만큼 있어야만 합니다. 보다 정확하게는 변환 관계를 나타내는 행렬의 원소들을 계산하기 위한 방정식들을 세워야하며 이 방정식들을 원소들의 개수만큼 세우기 위해서 최소한의 대응점 쌍들이 존재해야만 합니다.

호모그래피의 경우에는 3×3 행렬 중 맨 마지막(3,3에 해당하는 위치의 원소)의 값은 1로 두고, 그 외에 나머지 8개의 값들을 계산해야하며, 보통 한개의 대응 쌍에 대해서 방정식 2개를 세울 수 있기에 최소 4쌍의 대응점으로 방정식을 세우고 인자들을 계산할 수 있습니다.

하지만 일반적으로 4쌍의 대응점이 그 평면간의 관계를 완벽하게 대표한다고 보기 힘들 수도 있기 때문에 4개 보다 더 많은 N개의 포인트를 활용해서 호모그래피를 추정하는 방법들을 많이들 활용합니다. 가장 대표적으로 SIFT와 같이 영상의 keypoint 및 descriptor를 추출하는 알고리즘과 이렇게 추출된 값들에 대해 matching을 수행한 후 RANSAC과 같은 outlier estimator를 통해 inlier에 대한 값들만으로 호모그래피를 추정하는 것이죠.

그런데 이러한 feature based homography estimation 방식은 아쉬운 점들이 존재합니다. keypoint 및 descriptor가 잘못 추정이 되었을 때, 혹은 매칭이 잘못 되었을 때, 혹은 RANSAC이 outlier를 효과적으로 제거하지 못했을 때 등과 같이 추정에 오차가 발생할 수 있는 구간이 여럿 존재할 수 있게 되며, 또 여러 스탭으로 이루어져있다보니 속도적인 측면에서도 시간이 제법 걸릴 수 있게 됩니다.

따라서 최근에는 이러한 feature based 방식이 아닌 Deep learning network로 곧바로 호모그래피를 추정해버리는 방법론들이 제안되어 왔습니다. 물론 descriptor를 추정하거나 대응점들 간에 matching을 수행하는 방법 역시 deep learning으로 진행이 가능하나 위에서 언급한 일련의 과정(descriptor extraction – matching – homography estimator(RANSAC))과 같은 과정은 여전히 수행되기 때문에 일단 feature based라고 표현을 하였습니다.

아무른 이러한 deep learning based homography estimation 방법론들은 두 영상으로부터 4개의 offset 값을 계산하게 됩니다. 이 offset 값은 영상의 코너 4점이 어떻게 움직여야할지에 대한 offset 값에 해당이 되는데, 쉽게 말해서 영상의 해상도 내 (0,0) (0,W), (H,0) (H,W)에 해당하는 지점들이 얼만큼 움직였을 때 대응되는 영상과 정확히 일치하는지를 예측한다고 보시면 됩니다.

사실 어찌보면 Homography matrix 그 자체를 추론하도록 해도 되지 않느냐?라는 생각이 드실 수도 있습니다. 하지만 4개의 코너점의 x,y를 추론하는 값도 8개이며, 호모그래피를 구성하는 행렬 내 원소들도 8개의 값이기 때문에 서로 동등한 8개의 값을 추론하는 것이기에 크게 문제가 없습니다.

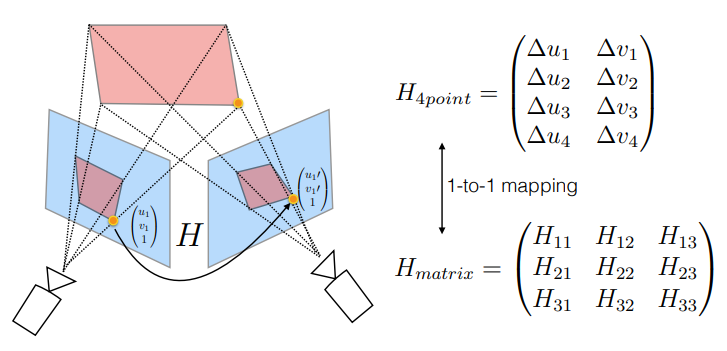
오히려 호모그래피의 8개의 원소들 값 간에는 scale이 다들 상이하기도 하고 일관성이 없기에 학습이 어려운 반면, 영상의 offset의 경우에는 픽셀 단위로 그 스케일 값이 그리 크지가 않아서 offset 방식으로 학습하는 것이 보다 학습이 더 잘된다고 합니다. 아무튼 이렇게 offset을 계산하게 되면 둘 사이에 대응점 4쌍을 구할 수 있게 되고 이 값들에 대하여 방정식을 풀어나감으로써 최종적인 호모그래피를 추정하게 됩니다.

이러한 딥러닝 기반의 호모그래피 추정 방식은 크게 지도학습 방식과 비지도학습 방식으로 나눌 수 있습니다. 지도학습 방식은 당연히 학습 때 GT값이 존재한다는 의미인데, 사실 두 영상간에 대응점에 대한 GT를 구하는 것은 상당히 번거롭고 귀찮은 일에 해당합니다.

이론적으로 Lidar 혹은 Depth Camera와 같이 3D 정보와 두 카메라 간의 relative pose 정보만 있으면 대응관계를 쉽게 계산할 수 있어서 해당 정보들을 모두 포함한 데이터셋으로 학습을 시킬 수도 있겠으나, 위에서도 설명드렸다시피 모델의 추론값이 영상의 각 코너점에 적용할 offset을 계산하는 문제로 풀다보니 Depth 정보를 토대로한 GT는 무언가 결이 조금 안맞다고 보여질 수 있습니다.

그래서 기존의 지도학습 기반 연구들은 그림2와 같이 하나의 이미지에 대하여 패치를 지정하고, 해당 패치의 각 코너에 랜덤한 offset을 적용 및 homography 연산을 수행하여 source region과 target region 구하는 합성 데이터 생성 방식으로 학습을 수행합니다.

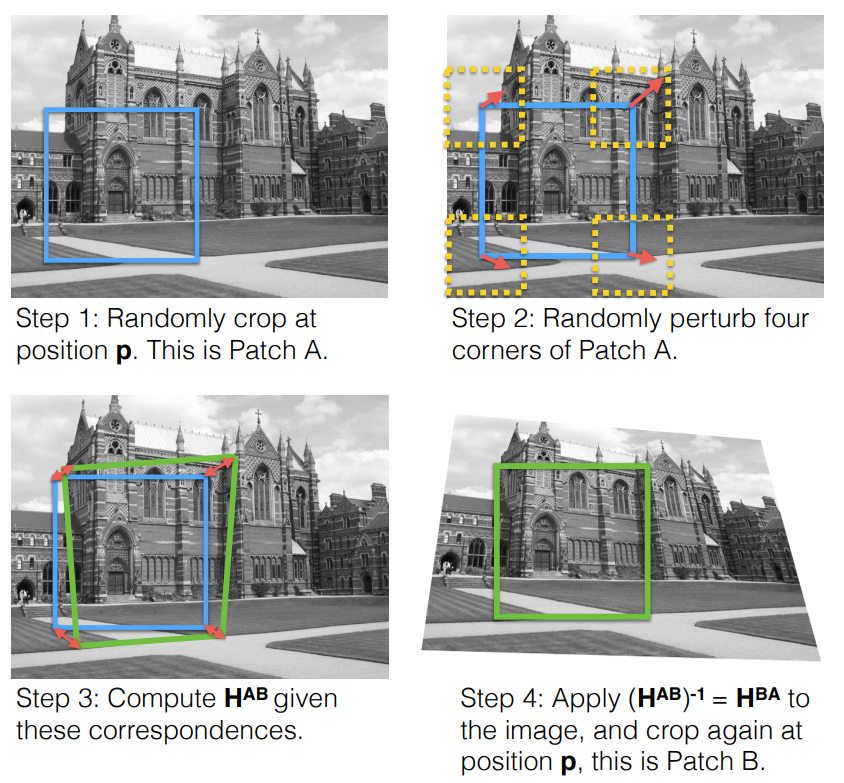
이러한 방식은 GT를 구하기 어렵다는 지도학습의 문제를 쉽게 해결할 수 있는 이점은 있었으나, 문제는 이러한 합성 데이터셋의 경우 데이터를 생성할 때 사용한 random perturb(step2)의 분포가 결국 한정적이기에 모델의 일반화 성능이 크게 떨어지게 됩니다. 요약하면 합성 데이터셋에서 나타나는 호모그래피의 분포와 실제 real 환경에서 발생할 수 있는 두 영상 간에 호모그래피 분포가 다를 경우 성능이 크게 하락할 수 있다는 것이죠.

따라서, 연구자들의 관심은 지도학습 방식이 아닌 정합이 맞지 않는 real dataset에서도 호모그래피 추정 학습을 가능케하는 비지도학습 방식으로 눈을 돌립니다. 비지도학습 방식도 매우 간단한데, 두 영상으로부터 모델이 계산한 호모그래피 값으로 실제 source image를 target image로 변환을 시킵니다. 그리고 이 warped source image와 target image 간에 픽셀 오차를 계산하는 방식으로 학습을 하는 것이죠.

지금까지의 내용을 그림 3을 통해서 정리해볼 수 있을 것 같습니다. 그림3-c의 비지도학습 파이프라인에서 각각의 세부 요소들에 대해 자세하게 보실 필요는 없으시고 그냥 대략적인 흐름으로 두 영상으로부터 H를 계산하고, 이 계사된 H로 영상을 sampling(spatial transformation)한 뒤에 Photometric loss를 계산하는구나~ 정도로 이해하시면 됩니다.

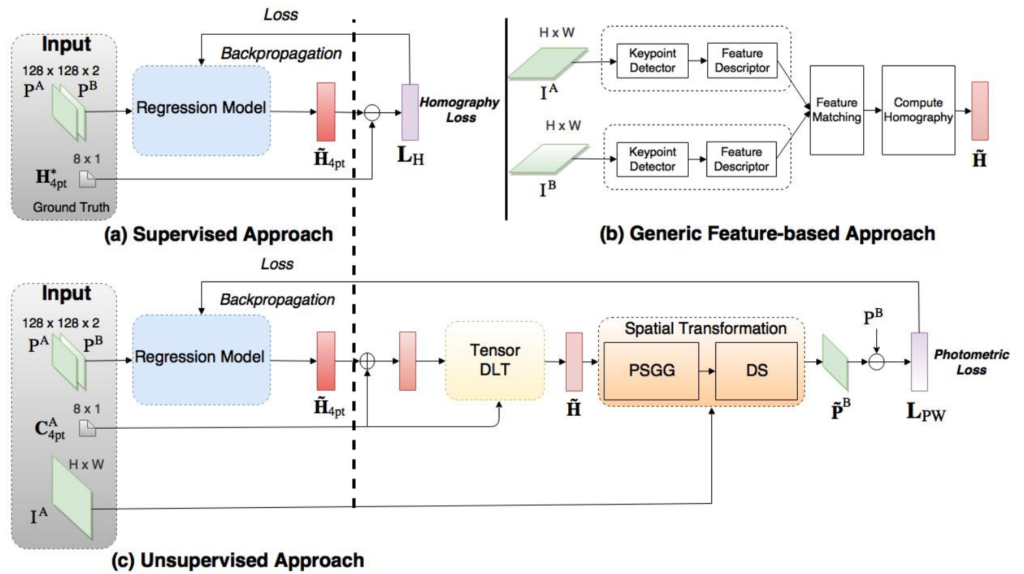
결과적으로 제가 리뷰드릴 논문 역시 비지도학습 방식의 호모그래피 추정 방법론이며, 본 논문에서 제안하는 기여는 무엇인지에 대해 이제부터 알아보도록 하겠습니다.

Intro

딥러닝 기반의 호모그래피 추정 방법론은 영상의 각 코너점에 대응되는 4개의 offset을 계산한다고 말씀드렸습니다. 본 논문에서도 이와 유사한 흐름으로 가려고는 합니다만 차별점은 호모그래피를 flow 형식으로 추론을 진행한다는 것입니다. 이전 방법론들의 파이프라인과 제안하는 논문의 파이프라인을 살펴보시면 더 쉽게 이해하실 수 있습니다.

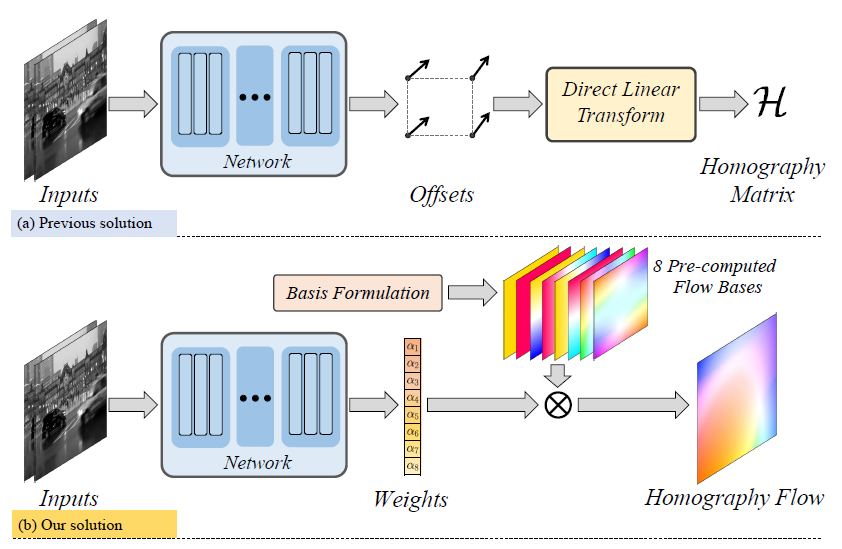
보시면 두 입력 영상을 넣어 네트워크로부터 offset을 계산하도록 하는 것이 아닌 8개의 가중치값을 추론하도록 시킵니다. 이렇게 추정된 가중치들은 초기에 미리 계산해둔 8개의 Flow bases에 weighted sum을 함으로써 최종적으로 Homogrpahy를 추정하게 됩니다. 이러한 flow based homography 방식은 특히나 두 영상이 small-baseline일 때 매우 효과적으로 동작할 수 있다고 합니다.

둘째로, 호모그래피는 8개의 자유도(DOF)를 가지고 있기 때문에 low-rank space로 볼 수 있습니다. 하지만 호모그래피를 추정하기 위해서 네트워크 내 연산되는 feature space는 그보다 훨씬 더 큰 rank를 가지고 있으며, 이러한 rank의 차이가 호모그래피의 부정확한 성능을 야기한다고 주장합니다.

조금 더 설명하면, 호모그래피는 결국 평면과 평면 사이에 관계만을 설명할 수 있기 때문에, multi-depth 혹은 동적인 객체가 영상 안에 다수 출몰하게 될 경우 하나의 호모그래피 행렬만으로는 이러한 대상들까지 모두 고려하여 대응관계를 설명할 수가 없게 됩니다.

결국 호모그래피 추정 방법론들은 동적인 대상 혹은 multi-depth 부분을 잘 제거하고 영상의 대표적이고 지배적인 region에 대해서만 잘 설명할 수 있는 호모그래피 추정을 하기를 원하는데, 이러한 영상 내 지배적인 호모그래피 추정을 위해서는 feature map의 high rank를 low rank로 잘 projection시킬 필요가 있다고 설명합니다.

이를 수행하기 위하여, 저자는 Low Rank Representation(LRP) block이라는 것을 새롭게 제안합니다. 해당 block은 normal CNN에다가 쉽게 붙이거나 땔 수 있는 매우 효율적인 모듈이라고 주장하며, 자세한 방식은 아래에서 설명드리겠습니다.

마지막으로 저자들은 새로운 loss function도 함께 제안하게 되는데, 해당 loss에 대해서 설명드리기 전에 사전 지식부터 간략히 소개드리면 기존의 비지도학습 기반 호모그래피 추정 방법론들은 warped image와 target image 간에 오차를 계산할 때 단순히 영상 레벨에서의 photometric loss가 아닌 feature level에서의 perceptual loss를 계산합니다.(뷰포인트 차이로 인한 픽셀의 밝기 값 차이를 완화시키고자.)

이때 단순히 imagenet으로 사전학습된 네트워크를 freeze하여 사용할수도 있겠으나, 보통은 end-to-end 방식으로 loss network도 함께 학습시키는 방향으로 학습이 진행이 됩니다. 이 네트워크를 학습시키기 위해서, triplet loss 방식으로 loss function을 사용하게 되는데 target image를 anchor로 두었을 때, target image와 warped source image 간에 관계를 positive sample, target image와 source image 간에 관계를 negative sample로 보고 positive sample은 가깝게, negative sample을 더 멀리 되도록 학습하는 것입니다.

여기서 저자가 주장하는 문제점은 우리가 원하는 (그리고 더 중요한) 방향은 positive sample들이 더 가깝게 지냄으로써 loss가 잘 떨어지는 것이지만, 실제로 수렴의 방향이 negative sample이 더 잘 떨어지는 방향으로 loss network가 학습이 된다고 합니다.

따라서 저자는 이러한 현상을 최대한 막고 task에 부합한 방향으로 학습이 잘 진행되도록 하기 위하여 Feature Identity Loss(FIL)이라는 것을 새롭게 제안합니다. 해당 loss의 대략적인 흐름은 warping하고 feature를 구하는 것과 feature를 구하고 warping을 하는 것이 서로 같아야한다는 loss function이라고 보시면 됩니다.

Method

그럼 방법론에 대해서 살펴보시죠. 가장 먼저 살펴볼 내용은 flow bases를 어떻게 계산하는지 입니다.

저자는 먼저 사전에 계산된 초기 8개의 homography bases를 만드는 과정에 대해서 설명을 하는데, identity homography matrix의 single element(e.g., h_{11} , h_{22] )들을 수정하여 8개의 호모그래피 행렬을 만든다음 이들을 영상 좌표에 적용하여 flow map을 생성합니다.

이렇게 계산된 homography flow들은 각 flow 내에 가장 큰 값과 QR decomposition을 토대로 normalization을 수행하게 됩니다.

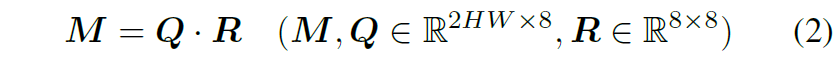
여기서 M의 각각의 컬럼들은 정규화된 호모그래피 flow를 의미합니다. QR 분해를 통해 Q의 컬럼들은 모두 직교화가 되었으며 이들은 자연스럽게 호모그래피의 subspace에 걸쳐 확장된 flow bases의 역할을 수행할 수 있게 됩니다. 이는 바꿔 말하면, 각각의 flow bases가 호모그래피 그룹의 원래의 공간에서 접선 공간에 위치해있다고 볼 수도 있습니다.

무언가 굉장히 선형대수학적인 내용들로 도배를 하다보니 저도 이해가 좀 어렵고 읽으시는 분들도 이해가 어려울 것 같은데, 요약하면 각각의 bases에 적용할 가중치를 정확히 예측함으로써 호모그래피 flow라는 것을 예측할 수 있도록 이러한 초기값 세팅을 선형대수학적으로 접근하여 잘 설계를 했다고 이해하시면 될 것 같습니다.

이러한 초기 homography flow bases의 생김새는 다음과 같습니다.

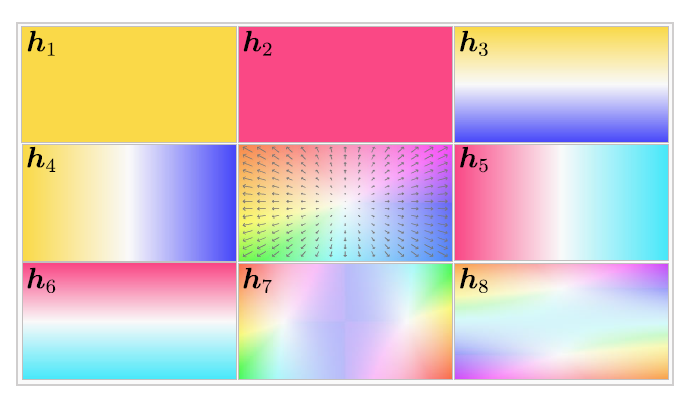
Homography Estimator with LRR Block

그 다음에는 LRR Block 및 모델 구조에 대해서 좀 살펴보겠습니다.

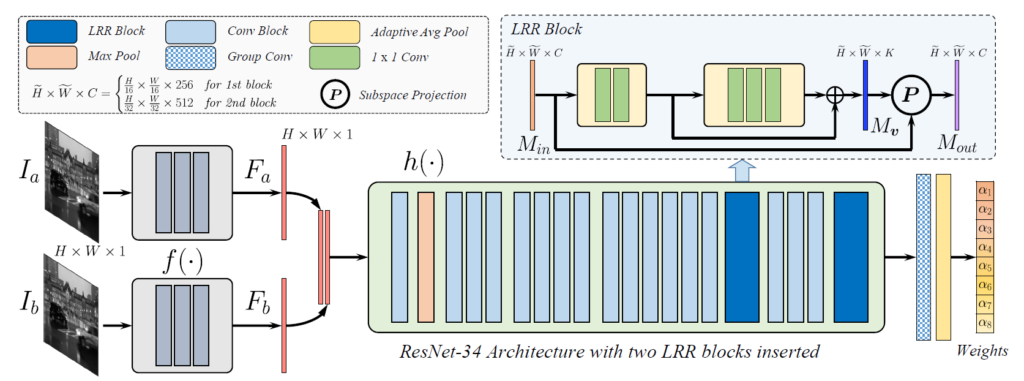
먼저 영상에 대하여 3개의 얉은 컨볼루션을 태워서 feature map을 추출합니다. 이렇게 추출된 feature map a와 b를 단순히 concat한 다음 ResNet 기반의 호모그래피 추정 모델에 태워서 값을 추론하게 됩니다. 여기서 본 논문은 이전의 논문들과 달리 flow 기반으로 동작하기에 offset이 아닌 8개의 weight을 추론하게 됩니다.

그리고 호모그래피 추정 네트워크에 뒷부분에서 LRR block이 2개 존재하게 되는데 이 LRR block은 shallow한 residual block 으로 구성이 되어 있습니다. 해당 블록의 최종적인 역할은 입력된 motion feature의 high rank를 잘 추려서 low rank로 projection하는 역할을 수행합니다.

보다 구체적으로 LRR block의 입력으로 들어온 Motion Feature M_{in} \in R^{H \times W \times K} 에 대하여 저자는 각각의 채널들에 속하는 feature map을 1D로 flatten 시킨 뒤 이러한 vector를 feature basis v_{k} \in {HW} 로 바라보았습니다.

따라서 저자들은 low rank motion만 남기고자 feature bases의 subspace 안으로 M_{in} 을 다음과 같이 투영시켜버립니다.

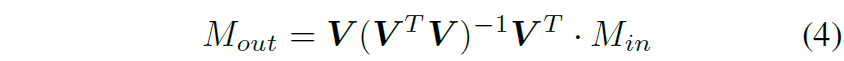
여기서 V는 [v_{1}, v_{2}, ..., v_{K}] 이며, 수식4에 (V^{T}V)^{-1}[ 연산을 적용한 이유는 feature bases들이 반드시 직교성질을 가진다는 보장이 없기 때문에, 해당 텀을 두고 정규화를 해줌으로써 직교성질을 가지도록 하기 위함이라고 합니다.

저자는 실제 구현 단계에서 이 LRR 블록을 총 2개를 두었으며, 차원을 축소하는 값 K를 16으로 두었다고 합니다. 16으로 둔 계기에 대해서 자세하게 말을 하지는 않았지만, 아마 아래 그림을 보았을 때 PCA의 y축 energy값이 K16에서 이미 100%를 채웠기 때문에 K를 16으로 둔 것이 아닐까 합니다.

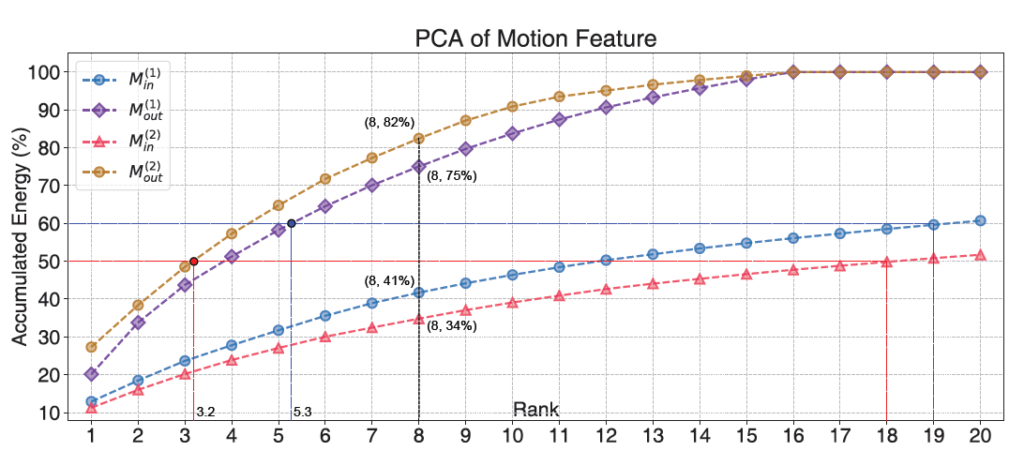
Robust Homography Estimation by LRR

지금까지 LRR 모듈의 구성 및 역할에 대해서 알아보았는데, 사실 이렇게만 놓고보면 LRR 모듈이 왜 필요한가에 대해서 감이 잘 잡히지 않을 듯 합니다. 그래서 저자들도 이 LRR 모듈에 대하여 구체적인 필요성에 대해 다시한번 언급을 진행하는데 해당 부분에 대해서 간략히 요약드리고자 합니다.

호모그래피는 (intro에서도 소개드렸다시피) 평면과 평면 간에 관계만을 설명할 수 있다보니 다중 평면이 존재하는 3D real world에서는 영상 전체에 대한 완벽한 관계를 묘사할 수 없습니다. 그리하여 이전의 연구들은 입력 영상으로부터 컨볼루션 레이어를 통해 마스크를 추출한 뒤 해당 마스크를 씌워서 중요하지 않은 영역(가령 동적인 객체 혹은 영상에서 매우 작은 범위만을 차지하는 영역)을 지워버리고 영상의 지배적인 영역만을 집중해서 모델이 호모그래피를 추정하도록 하게 합니다. (마치 feature based 방식에서 RANSAC을 통해 outlier를 제거한다는 것과 유사하게 생각하시면 됩니다.)

즉 저자들이 생각했을 때 영상 내 지배적인 평면(호모그래피가 고려해야할 영역)을 제외한 모든 영역들은 outlier로 볼 수 있다는 것이며, 이러한 outlier들은 motion feature의 각 채널들(rank)로 볼 수 있다는 것입니다. 따라서 LRR 모듈을 통해 효과적으로 motion feature의 outlier들을 제거함으로써 지배적인 영역에 초점을 맞춘 좋은 호모그래피를 추정할 수 있다는 의미이죠.

실제로 실험적 결과에서 저자들은 이전의 마스킹 방식 보다 자신들의 LRR 모듈이 훨씬 더 효과적으로 outlier들을 제거함으로써 정확한 호모그래피를 추정함을 보여줍니다. 이에 대한 결과들은 실험 섹션에서 다루겠습니다.

Triplet Loss with Feature Warp-Equivaraince

다음은 저자가 새롭게 제안하는 loss function에 대한 설명입니다. loss network를 학습하기 위해서 triplet loss 형식을 사용한다고 말씀을 드렸는데 이는 아래와 같습니다.

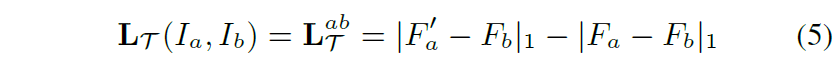
여기서 F'_{a}, F_{a}, F_{b} 는 각각 warped source feature map, source feature map, target feature map에 해당하게 됩니다. 즉 호모그래피를 통해 변환된 source feature는 target feature와 정합이 맞아야하며, 반대로 source feature map과 target feature map은 오정합 되어있는 상태니 계속 loss 값이 가져야만 한다는 것이죠.

대부분의 경우에는 이러한 loss function으로 호모그래피 추정 모델 및 loss network 모두 학습을 잘 시킬 수 있지만, 때때로 뒷단에 negative sample term에 편향되어 학습이 진행되는 경우가 있다고 합니다. 물론 negative term도 모델 학습에 좋은 영향을 줄 수 있지만 사실 가장 중요한 것은 positive term이 잘 수렴되도록 하는 것입니다.

따라서 저자는 아래 수식과 같이 warped image를 feature 도메인으로 변환시킨 결과와 feature domain을 warping하였을 때의 결과 값이 같아지도록 하는 제약조건을 새롭게 추가함으로써 loss network가 정합의 의미 및 spatial alignment에 더 초점을 두도록 학습을 시킴으로써 모델 학습의 안정화를 의도했다고 합니다.

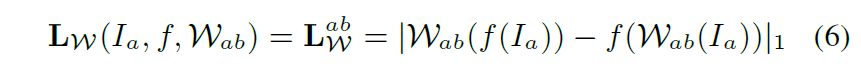
Experiments

그럼 실험 결과들에 대해서 다루고 리뷰 마무리 짓도록 하겠습니다.

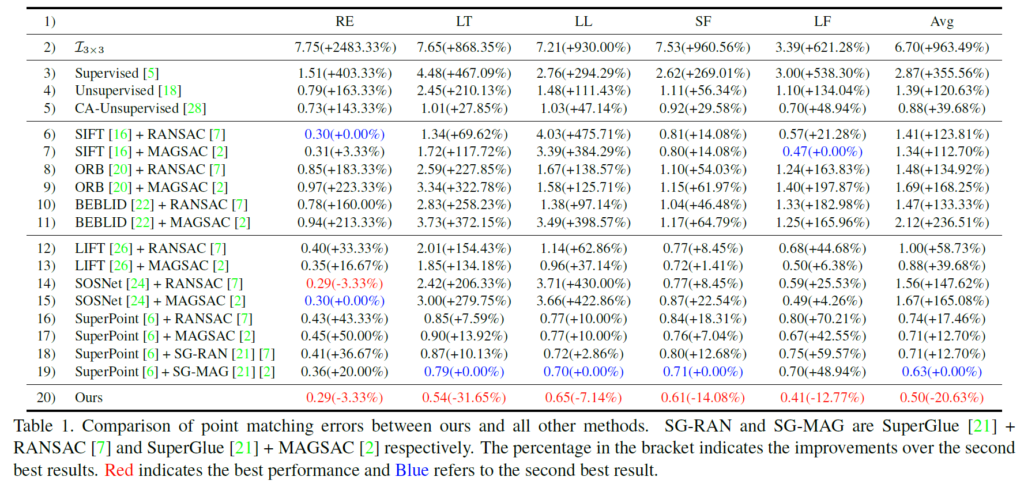
위에 표 1은 deep learning based, feature based 그리고 제안하는 방법론에 대한 비교 성능을 보여주는 표입니다. 평가 지표는 대응점들에 대한 L2 distance의 평균을 계산한 것이며, RE, LT, LL SF, LF는 각각 REgular, Low-Texture, Low Light, Small Foregrounds, Large-Foregrounds로 구분을 짓는다고 합니다. 즉 앞에 Regular가 가장 쉬운 케이스에 속하고 그 외에 나머지들은 대응관계를 계산하기 힘든 각 특징별 어려운 장면들이라고 보시면 될 것 같습니다.

가장 먼저 눈에 띄는 점은 제안하는 방법론이 모든 상황에 대해서 가장 좋은 성능을 보여준다는 점입니다. 게다가 같은 Unsupervised 방법론이며 베이스라인 방법론에 해당하는 5번째 행 CA-UJnupservised랑 성능을 비교하였을 때 그 성능의 차이가 매우 크다는 것을 볼 수 있습니다.(0.79 vs 0.29)

실제 정성적 결과에서도 자신들의 경우 정합이 잘 맞는다는 것을 보여주고 있습니다만 경향성에 대해서 가볍게 훑어 보시면 될 것 같습니다.

Ablation study

다음은 ablation study에 대한 내용입니다.

가장 먼저 outlier를 제거하는 방식으로 Mask를 사용하고 호모그래피 추정 모델의 예측값도 offset인 경우가 베이스라인이라고 하였을 때 평균적으로 0.88에 픽셀 에러값이 발생합니다.

여기서 offset을 Basis로 바꾸었을 때 평균 픽셀 에러 값은 0.05 감소하는 모양입니다. Regular 상황에서는 0.2로 제법 많이 향상되는 반면에 LT, LL, SF와 같은 보다 대응관계 추정이 어려운 상황에서는 성능이 개선되지 못하고 오히려 떨어지는 모습이네요.

하지면 여기서 Loss network를 학습할 때 사용하는 loss function에 Feature Identity Loss를 추가하여 학습을 하게 될 경우 SF 상황을 제외하고 성능들이 많이 개선된 것을 확인할 수 있습니다. 이는 즉 loss network의 학습 안정성을 잘 잡아서 보다 정합관점에서 정확한 호모그래피를 추정하도록 학습 방향이 잡힌 것을 간접적으로 확인하실 수 있습니다.

그다음에는 Masking 방식이 아닌 LRR 방식으로 outlier를 제거하였을 때의 성능인데요 사실 이 경우 Regular 뿐만 아니라 거의 모든 상황에서 성능 향상이 크게 발생하는 것을 확인하실 수 있습니다. 평균 픽셀 에러 값도 0.6으로 매우 줄어든 것을 볼 수 있는데.

아무래도 Masking 방식은 3개 정도의 매우 얕은 컨볼루션 레이어로 입력 영상들에서부터 outlier region을 찾아야하다보니 small foreground 혹은 low light 등 영상 내 정보들을 쉽게 특정하기 힘든 경우 부정확한 마스크가 추출되는 반면, LRR 모듈은 feature의 rank를 줄인다는 컨셉으로 접근하게 되니 보다 좋은 성능을 기대할 수 있었던 것 같습니다.

그래서 최종적으로 LRR 모듈과 Basis prediction 그리고 FIL을 추가하였을 때 평균 픽셀 에러 값이 0.5로 매우 향상된 것을 확인할 수 있습니다.

결과적으로 이렇게 잘 학습을 시킨 덕분에 휴대폰으로 촬영한 unseen photo에 대해서도 정확한 호모그래피를 추정하였다고 저자는 주장합니다.

결론

oral paper 답게 contribution 하나하나들이 매우 신중하고 잘 설계한 방법이다라는 느낌을 강하게 받았습니다. 그 덕에 이전 베이스라인 방법론과 비교하여 매우 큰 성능 향상을 보여주었구요. 게다가 architecture도 아직 Resnet34에 두 영상 간에 대응관계도 단순히 concat으로 fusion하는 식의 매우 단순한 방법을 채택함에도 불구하고 성능에 큰 향상을 일으켰기 때문에.. 대단하다는 말과 더욱 성능 향상을 일으킬 여지가 있다는 점이 마음에 듭니다.

다만 저자가 논문에서도 밝혔다시피, 제안하는 방법론은 small baseline에서는 강건하게 동작하는 반면 large baseline, 즉 두 영상 간에 시차가 큰 경우에는 부정확한 호모그래피를 추정할 가능성이 높다고 합니다. 아무래도 초기에 미리 계산해둔 homography flow bases들의 설정값 때문인 것으로 파악되는데 선형대수적 개념이 너무 많이 들어가다보니 아직 완벽하게 해당 논문을 이해하지 못한 시점에서 왜 large baseline은 잘 안된다는 것인지는 모르겠네요.