[CVPR 2023] MarginMatch: Improving Semi-Supervised Learning with Pseudo-Margins

오랜만에 Semi-supervised learning 관련 연구를 리뷰해보겠습니다. 현재 실험 중 pseudo-labeling 에 대한 새로운 접근을 시도 중에 읽게되었습니다.

MarginMatch: Improving Semi-Supervised Learning with Pseudo-Margins

• Paper: MarginMatch: Improving Semi-Supervised Learning with Pseudo-Margins
• Supplemental: Link
• Author Video: None
• Code: GitHub (X. Delayed)

---

Introduction

시작에 앞서 Semi-supervised learning 연구는 보통 ~Match로 끝나는 경우가 많은 듯 합니다. 지난번 제가 SimMatch라고 CVPR 2022에 게재된 연구를 리뷰한 적도 있는데 이 역시 Semi-SL 이었습니다. 이번에 제가 리뷰하려는 논문은 2023 CVPR에 게재된 연구인데요. 그런데 아직까지 introduction에서 2020년에 공개된 FixMatch 와 FlexMatch 를 언급하며, 이에 문제점을 해소할 대안을 마련했다고 글을 시작한다는 것이 신기할 따름입니다. (그만큼 FixMatch가 Simple is best를 보여주었던 것은 아닌지….)

각설하고 해당 논문을 이해하기 위해서는 FixMatch 와 FlexMatch를 이해해야합니다. 해당 논문에서 다룬 정도로 아주 간단하면서도 코어한 내용만 여기서 다뤄보도록 하겠습니다.

우선 Semi-supervised learning 은 소량의 labeled dataset과 대량의 unlabeled dataset을 사용하여 모델을 학습시키는 방식에 대한 연구입니다. Semi-supervised learning 의 근본이라고 한다면 단연 손꼽힐 수 있는 것은 FixMatch 입니다. FixMatch를 비롯하여 그 후속을 잇는 ~Match 로 끝나는 연구들은 대부분 다음 2가지의 기술을 메인으로 가져가고 있습니다.

1. Consistency regularization
   • Consistency Regularization (일관성 정규화)는 한 이미지에 서로 다른 왜곡 (augmentation)을 주더라도 모델은 유사하고 일관된 예측을 출력해야한다는 가정하에 Regularization을 설정하는 기술입니다. 동일한 이미지에 weakly/strong augmentation을 각각 적용하더라도 모델은 이미지의 공통의 특성을 파악하도록 학습되어야 합니다.
2. Pseudo-labeling
   • Pseudo-labeling 은 말 그대로, 모델의 예측값을 Pseudo-label로 사용하겠다는 기술입니다. semi-supervised learning 에서 대량의 unlabeled dataset을 supervised learning 방식으로 학습에 사용하기 위해, 모델의 예측값을 pseudo-label로 설정합니다.

위에 서술된 두 가지 기술을 아래 그림 (FixMatch) 과 함께 살펴보겠습니다. 1번인 consistency regularization은 아래 그림에서 전혀 다른 augmentation이 적용된 말 그림 두개에 대해 모델은 같은 output을 발생할 수 있도록 만들자 라는 기술입니다. 그리고 2번인 Pseudo-labeling은 다소 왜곡이 적은 weakly augmentaed image에 대한 예측값을 pseudo-label로 사용하여 아래 strong 이미지를 학습시키자는 기술입니다.

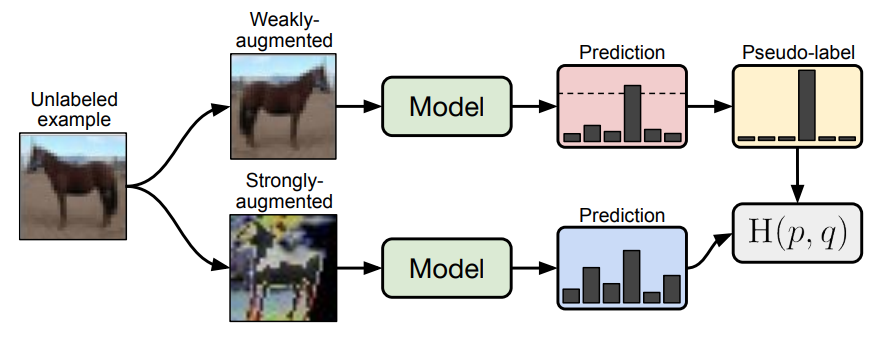
이제 어느정도 컨셉에 대해서는 이해하셨을 것 같으니, FixMatch에 대해 설명을 이어가보겠습니다.

FixMatch의 핵심은 모든 weakly 입력의 예측값을 pseudo-label로 사용하는 것이 아니라는 것입니다. 모델의 output은 N (=number of class) 개의 벡터로 구성됩니다. 보통 softmax를 태운 뒤 가장 높은 확률 값을 보이는 클래스로 결과를 예측해냅니다. FixMatch에서는 예측 확률이 가장 높은 값이 특정 threshold 이상인 샘플에 대해서만 unlabeled sample 학습에 사용하였습니다. 쉽게 말해 Entropy가 낮은 데이터셋 혹은 모델이 확실하게 하나의 클래스다 라고 예측한 데이터셋에 대해서만 학습하겠다는 거죠. threshold 가 0.9라고 한다면? 0.8로 A라는 클래스라고 예측한 이미지는 학습에 사용하지 않겠다는 소리입니다. 그럼 나머지 라벨들은 어떻게하죠? 그냥 학습에 사용하지 않는 것입니다. 확실한 데이터에 대해서만 unlabeled 샘플 학습에 사용하게 됩니다.

따라서 이렇게 구한 FixMatch는 unlabeled 데이터에 대해 다음 수식과 같은 배치 별 consistency loss를 최소화합니다.

(참고로 ~Match로 끝나는 연구는 supervised loss와 unsupervised loss로 구성됩니다. supervised loss는 우리가 흔히 아는 cross entropy loss를 사용합니다. 소량의 라벨 데이터셋을 학습하기 위해 사용하는 것이죠. 그리고 아래 수식은 이제 대량의 unlabeled dataset을 학습하기 위한 unsupervised loss를 의미합니다. 지금부터 아래에 나열될 FixMatch, FlexMatch, MarginMatch의 L_u는 모두 unsupervised loss를 의미합니다)

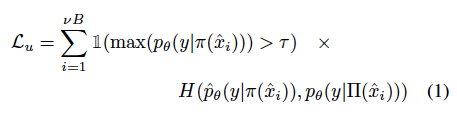
\gamma는 위에서 말한 confidence threshold를 의미하며, \phi와 Π는 weak, strong augmentation을 의미합니다. 아, 추가로 H(p, q)는 확률분포 p, q 사이의 cross entropy 를 의미합니다.

그런데 이렇게 되면, FixMatch에서 학습에 사용할 수 있는 데이터가 현저히 줄어들곤 합니다. 너무 엄격한 threshold 기준으로 인해, 확증편향은 예방할 수 있었던 건 사실이지만, 클래스마다의 난이도 차이가 고려되지 못할 수 있습니다. 고양이 데이터는 유난히 쉬워서 0.9라는 cut이 적합할 순 있지만, 강아지 데이터는 워낙 outlier 가 즐비한다면? 0.9로 걸러지는 데이터가 너무 적어지는 상황이 발생하게 됩니다.

그래서 FlexMatch는 이름에서처럼 유연한 threshold를 설정하기로 하였습니다. 가령 고정된 threshold값이 아닌 샘플 개수가 적은 클래스는 학습 난이도가 높다고 판단하여 threshold를 adaptive 하게 낮춤으로써 학습 샘플을 더 많이 선택할 수 있게 변경합니다. 계산하는 법은 간단합니다. 클래스 c에 대한 학습 상태 \alpha_c는 클래스 c에서 예측되고 고정 threshold \gamma를 통과하는 라벨링되지 않은 수로 계산이 간단하게 가능해집니다. 그리고 클래스 c에 대한 임계값 T를 구하는 건 아래 수식 (3) 과 같습니다.

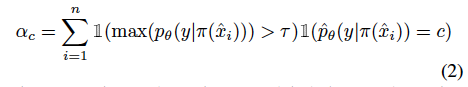
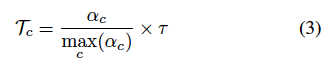
결과적으로 unlabeled loss는 다음과 같이 도출할 수 있게 됩니다. 참고로 T_c^t가 앞서 구한 c 클래스에 대한 adaptive threshold가 됩니다.

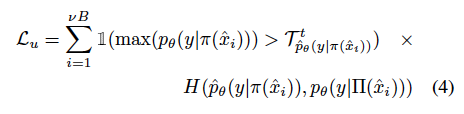
결국 기존 두 방법론은 Pseudo-label 뽑고 학습에 사용 여부를 결정하는 기준이 달라졌다는 차이가 있다고 정리할 수 있겠네요. 그렇다면 저자가 생각하는 문제점은 무엇일까요? 바로 pseudo-label을 뽑을 그 때의 모델 상태만을 고려한다는 점입니다. 저자의 말에 따르면.. 앞서 반복적으로 학습해오면서 보인 모델의 상태를 고려하지 않고, 가장 마지막 모델의 output만을 사용한다면 ‘근시안적인’ 관점만을 제공하기 때문에 정보가 충분하지 않다고 합니다. 또한 over-confidence 라고 모델이 틀렸음에도 불구하고 높은 확신도를 가지고 있어 오히려 pseudo-label이 실제 GT와 달라서, 모델 학습에 악 영향을 미치는 경우가 발생하기도 합니다. 아래 그림이 바로 FixMatch와 FlexMatch 모두에 대해 잘못된 pseudo-label을 사용하여 학습에 사용되는 예시입니다.

그래서 저자는 가장 마지막 iteration에서의 confidence만을 고려하는 것이 아니라, 학습이 진행되며 발생한 모든 모델의 ‘behavior’을 모니터 하고자 하였습니다. 이를 위해 Pseudo-margin 이라는 개념을 도입하여 학습 및 일반화에 대한 pseudo-label의 기여도를 추정하고자 하였습니다. 그래서 저자가 제안하는 모델의 이름이 MarginMatch입니다. pseudo-margin은 모델 출력의 신뢰도를 측정하고, 올바른 출력과 그렇지 않은 출력 사이의 차이를 정량화하는 기술입니다. 따라서 학습 과정 중 t번째의 pseudo label이 그동안 학습하면서 얼마나 다이나믹하게 달라졌는지 그 차이를 찾게되는 것이죠. 결국 핵심 포인트는 “학습 과정 중 반복에 걸쳐 잘못된 pseudo-label의 특성” 을 찾도록 모델을 학습하는 방법입니다.

Proposed Approach: MarginMatch

MarginMatch 역시 weakly/strong 증강 및 pseudo-labeling 과 함께 consistency regularization 을 활용합니다. 그러나 라벨이 없는 샘플을 학습에 사용할지 여부를 결정할 때, 모델의 현재 학습 시점의 confidence만 사용하는 대신 모델 출력의 Margins (confidence의 척도)를 통해 unlabeled 샘플의 training dynamics 모니터링 합니다. 결국 예측값이 학습을 반복하며 얼마나 바뀌었는지를 정량화하는 메트릭 정도로 이해하시면 좋을 것 같습니다.

우선 Margin이라는 지표는 할당된 기준값 레이블에 해당하는 logit과 가장 큰 다른 logit 사이의 차이를 정량화하는 지표입니다. 즉, 이 지표를 통해 그동안 학습하면서 얼마나 예측값의 변동이 있는지를 정량화하여 나타낸 것이라 할 수 있습니다. 그런데 Semi-SL에서는 unlabeled 에 대한 기준값인 GT를 사용할 수 없습니다. 따라서 저자는 GT가 아닌 Pseudo-label을 기준점으로 사용하고자 하였고 이를 Pseudo-Margin (PM) 으로 재정의하였습니다. c를 pseudo-label(예측값의 최대값)이라고 하면, 이제 c에 대한 \hat{x}의 값은 다음과 같이 iteration t에서 계산할 수 있습니다.

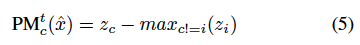
여기서 z_c는 할당된 pseudo-label c에 해당하는 logit 이고, max_{c!=i}(z_i)는 c와 다른 레이블 i에 대응하는 가장 크기가 큰 또다른 logit입니다. 결국 앞서 말한 Margin에서 기준점이 t번째 학습에서의 Pseudo-label로 변화한 것을 확인할 수 있습니다. t번째에서의 PM을 구했으니, 학습 과정 모두를 반영한다고 했던 저자의 의견을 반영하기 위해.. 학습 시작부터 t번까지 c에 대한 모든 마진을 평균화하여 다음과 같은 Average Pseudo Margin을 구하게 됩니다.

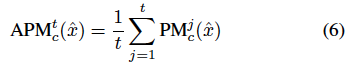
이 때 이전 iteration을 t’ 라고 해봅시다. t’에서의 pseudo-label c’가 c와 다르다면, t’까지는 c’에 의해서 평균 계산이 수행되게됩니다. 즉, c’에 대한 모든 마진을 1부터 t’까지 평균화합니다. 결국 학습이 반복되며 누적된 모든 클래스에 대한 pseudo-margin 벡터를 유지하고, pseudo-label c의 누적된 pseudo-margin 값을 동적으로 찾음으로써 iteration t에서의 APM^t_c를 구하게 됩니다.

그럼 APM이라는 건 어떤 영향을 줄까요? 학습이 반복되며 t의 pseudo-label c와 자주 일치하지 않고, 예측 라벨이 계속 변동되는 경우 c에 대한 APM은 음수일 가능성이 높습니다. (즉 낮은 값을 가진다) 마찬가지로 모델이 \hat{x} 클래스에 대해 불확실한 경우 클래스 c에 대해 ARM 도 낮은 값이 반영됩니다. 이는 클래스 확률 분포의 엔트로피가 반영되기 때문입니다. (즉, 불확실하다는 건 엔트로피가 높다는 것이기 때문) 이를 바탕으로 MarginMatch는 할당된 pseudo-label c의 APM을 활용하고, 이를 APM threshold와 비교하여 APM이 낮은 pseudo-label이 지정된 샘플이 마스킹 되는 것으로 설명을 마무리 할 수 있을 것 같습니다.

(아래 수식에서 FixMatch의 confidence 부분이 AM으로 대체된 걸 확인할 수 있죠? \gamma^t는 학습 t번째에서의 APM임계값입니다. 이건 아래 섹션에서 어떻게 결정하는지 추가로 설명합니다.)

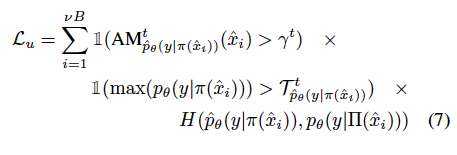
그리고 이렇게 구한 unsupervised loss는 supervised loss와 가중합을 통해 최종 모델의 loss 설명이 마무리되었ㅅ브니다.

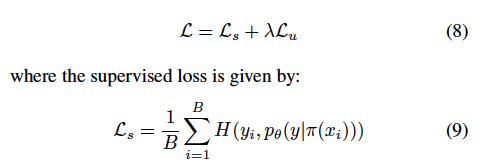
Average Pseudo-Margin Threshold Estimation

저자는 라벨이 없는 샘플의 훈련 과정을 분석하여, Error 혹은 잘못 라벨링된 샘플을 강제 지정함으로써 APM \gamma^t를 추정하고자 하였습니다. 즉, 잘못 라벨링된 샘플 E를 생성하기 위해, 학습 시작 시 존재하지 않은 클래스 C+1에 할당하는 unlabeled 하위집합을 랜덤샘플링하여 Unlabeled pool에서 제거하였습니다. 이렇게 잘못 라벨링된 샘플의 목적은 unlabeled 샘플 학습 과정을 트랙킹하여 잠재적으로 잘못라벨링된 pseudo-label 컷오프를 추정하기 위함이라고 합니다.

E의 예시는 원래 클래스 C 중 하나에 속해야 하기 때문에, 존재하지 않는 새로운 클래스 C+1에 할당되면 레이블이 잘못 지정된 것입니다. 모든 U unlabeled 데이터 샘플과 마찬가지로 E의 잘못된 라벨이라는 특별히 생성한 class에 대해 APM^t_{C+1}를 계산하지만, U의 라벨이 없는 샘플과 달리 E의 샘플들은 고정된 C+1이라는 클래스를 갖게 됩니다. U에서 라벨이 없는 샘플의 학습 과정을 모방하기 위해 strong aug.를 사용하여 E에서 잘못된 샘플의 loss를 계산하게 됩니다. 즉, B의 잘못된 샘플 배치가 주어졌을 대의 loss는 다음과 같습니다.

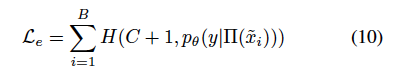
따라서 iteration t에서 앞서 구한 오류 샘플의 APM을 사용하여 APM의 threshold \gamma^t를 선택하게 됩니다. 최종적인 Losss는 아래와 같습니다.

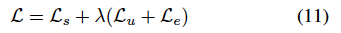
Experiments

(1) CIFAR-10, CIFAR-100, SVHN, and STL-10

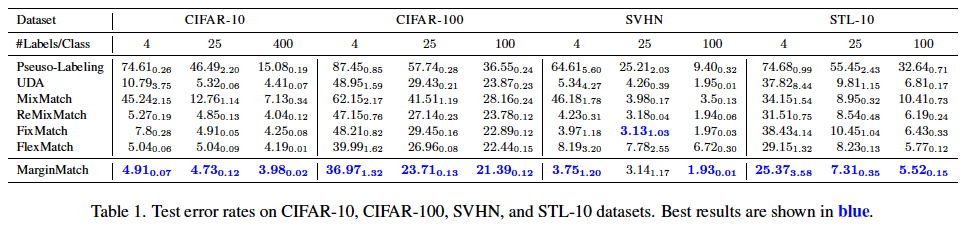
Semi-supervised learning 에서도 active learning 과 동일하게, 서로 다른 매개변수 초기화를 사용하여 5번의 실행에 대한 오류 ratio와 평균 및 표준편차를 리포팅합니다.

아래 테이블 중 Labels/Class는 소수의 라벨 데이터셋을 무작위로 샘플링하여 사용하였다고 합니다. CIFAR-10 CIFAR-100 모두에서 정확도를 향상시키는 것을 확인할 수 있었다고 합니다. 특히 CIFAR-10에서 FlexMatch에 비해 성능을 향상시키면서 표준편차는 유지하는 결과를 확인하였습니다. CIFAR-100에서는 훨씬 더 큰 성능 향상을 가져왔다 등등… 특별한 분석은 없이 최고다! 정도로 끝내네요..

사실 Semi-sueprvised 에서 비교하는 실험은 또 아래와 같이 얼마나 빨리 수렴하느냐, 에 대한 지표도 제시하였습니다. 그 결과는 아래와 같은데요. 클래스 당 4개의 레이블이 있는 모든 데이터셋에서 MarginMatch가 FlexMatch와 비슷한 수렴 속도를 보이고, 동일한 계싼 비용으로 ResNet-50을 사용하는 다른 SSL 방법보다 성능이 뛰어나다고.. 합니다.

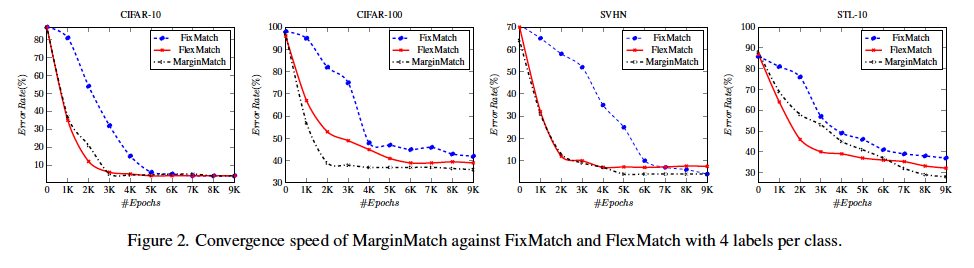
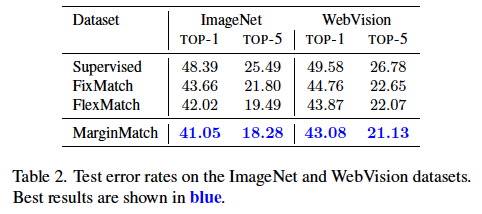
간단한 데이터셋 말고도 ImageNet, WebVision과 같은 데이터셋 결과도 보였는데요. sImCLR과 같은 방식은 높은 성능 달성하긴 하지만 계산 비용 측면에서는 MarginMatch가 훨씬 유리하다고 언급하고 끝입니다

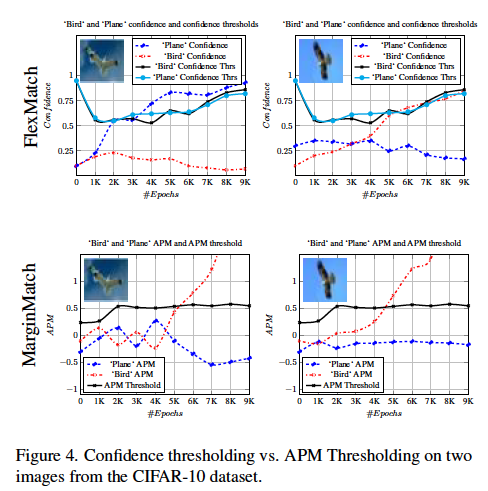
Ablation Study

Margin Match 효과에 대한 정성적 결과인데요. 배경이 유사한 두 개의 새 이미지에서 위쪽은 새와 plane 클래스에 대한 신뢰도 및 FlexMatch의 임계값의 진행상황을 보여주고, 아래쪽은 APM과 함께 MarginMatch의 APM 임계값의 진행상황을 보여주었습니다. 그 결과 오른쪽 이미지에서 MarginMatch의 경우 학습이 진행됨에 따라 새 클래스에 대한 APM이 점점 강해지는 것을 확인할 수 있었다고 합니다.

---

제가 Semi-supervised learning 이 완벽하게 팔로업이 안되어있기 때문일까요? 아니면 해당 연구의 필요성에 대해 완전히 설득되지 못한 탓일까요? 분석도 그 결과도 신통치 못한 그런 연구였던 것 같습니다. 다음엔 조금 더 좋은 논문을 리뷰해보도록 하겠습니다.