안녕하세요, 양희진입니다.

이번에도 6D pose estimation 논문을 가져왔습니다. single-stage로 pose를 추정한다고 해서 해당 논문을 구현한 코드를 보니correspondence-extraction 모델에 따라 loss를 보면 어떤 correspondence-extraction 모델을 쓸지에 따라 loss term을 다르게 적용하는 것을 보시면 이해하실 것 같습니다.

리뷰 시작하겠습니다.

Abstract

대부분의 6D pose estimation 프레임워크는 먼저 신경망 구조로 이루어진 네트워크에 의존하여 3D 오브젝트의 keypoint와 2D 이미지 위치 간의 correspondence을 설정한 다음, RANSAC-based의 변형된 PnP(Perspective-n-Point) 알고리즘을 사용합니다. 그러나 이 2-stage 프로세스가 완전한 방법은 아닙니다. 첫째로 다들 아시다시피, end-to-end 학습이 불가능합니다. 둘째, 학습은 최종 6D pose estimation을 올바르게 반영하지 못하는 surrogate loss에 의존합니다. 이번 논문에서는 correspondence에서 6D pose를 direct regression하는 아키텍처를 도입합니다. 각 3D keypoint에 대한 후보 correspondences 그룹을 입력으로 받아 각 그룹 내 대응의 순서는 무관하지만 그룹, 즉 3D keypoint의 순서는 고정되어 있다는 사실을 고려합니다. 저자가 제안한 아키텍처는 일반화가 되어 있기 때문에, 기존의 correspondence-extraction 네트워크와 함께 활용하여 1-stage 6D pose estimation를 수행할 수 있다고 합니다.

1. Introduction

2D-3D correspondence를 설정한 다음 RANSAC-based PnP 알고리즘을 사용하여 Pose를 계산하는 게 일반적인 방법입니다. 하지만, 해당 방법은 효과적이지만 몇 가지 약점이 존재하는데요.

약점 1.

학습하는데 사용되는 loss function은 pose 추정이라는 실제 목표를 반영하지 않고 2D error를 최소화하는 것에 집중하므로 해당 error와 pose 정확도는 딱히 관계가 없음. 그림1(a)을 보면 average 2D error가 동일한 2D-3D의 correspondence은 서로 다른 pose를 추정하는 것을 초래할 수 있습니다. 여기서 언급되는 “Average 2D error”는 2개의 2D 이미지 point 집합 간의 차이를 측정하는 데 사용되는 지표입니다. correspondence를 사용하여 2D 이미지 포인트를 3D 공간으로 연결시켜주지만, 2D 이미지는 3D 공간의 완벽한 projection이 아니기 때문에 해당 변환은 결국 근사를 시켜줘야 하는데요. 해당 근사화 과정에서 발생하는 오차는 해당 Average 2D error로 측정할 수 있습니다. 즉, 동일한 correspondence를 가지고 있더라도 실제로는 서로 다른 pose 추정값이 발생할 수 있다는 의미입니다. 뿐만 아니라 noise도 error 증가하는 원인이 될 수도 있습니다.

약점 2.

2-stage process는 ene-to-end 학습이 불가능합니다.

약점 3.

처리해야 할 대응이 많을 경우 반복적인 RANSAC은 시간이 많이 소요됩니다. 원칙적으로 end-to-end 프레임워크는 딥러닝 기반의 RANSAC을 활용하고, 다른 네트워크가 correspondence로부터 pose 추정을 수행함으로써 설계할 수 있습니다. 그러나 많은 outlier들이 있을 때 시간이 많이 걸리는 RANSAC의 특성과 그림1(b)에서 볼 수 있듯이 correspondence 순서가 결과 포즈에 영향을 미치기 때문에 해당 솔루션의 반복성이 좋지 않아 end-to-end 학습 가능한 네트워크에 포함하기에 적합하지 않습니다.

20년 당시까지 keypoint localization과 6D pose estimation을 함께 처리할 수 있는 end-to-end 프레임워크는 아직 존재하지 않았다고 합니다. 이 논문에서는 각 3D object keypoint에 연결된 3D와 2D correspondences 그룹에서 6D pose를 direct regression하는 간단하면서 효과적인 네트워크를 도입하여 문제를 풀어가려고 합니다. 해당 논문에서 사용되는 아키텍쳐는 각 그룹의 대응 순서는 무관하다는 것을 명시적으로 encoding하는 동시에 그룹의 순서가 고정되어 있고 3D keypoint 순서와 일치하다는 사실을 활용한다고 합니다.

2. Related Work

입력 이미지에서 keypoint를 detect한 다음 설정된 2D-3D correspondence에 대해 RANSAC-based PnP 알고리즘을 수행하는 것은 6D pose estimation 문제를 해결하는 고전적인 방법입니다. 그러나 이러한 전통적인 방법은 심각한 occlusion과 clutter한 배경이 있는 경우 여전히 안 좋은 성능을 보이는데요.

딥러닝이 발전함에 따라 최근에는 이미지로부터 바로 파라미터를 추정하는 direct regression method가 있습니다. 하지만 이러한 method는 K(intrinsic parameter)을 이용하는 indirect method인 2D-3D correspondence로부터 PnP-RANSAC을 적용하여 추정하는 것 보다 성능면에서 좋지 못한 한계가 있습니다. 하지만 저자는 이러한 indirect method는 카메라의 pose에 제약을 받기 때문에 2D-3D correspondence가 서로 독립적이지 않은 이러한 사실을 활용했다고 합니다. 해당 논문에서의 목표는 이러한(correspondence + RANSAC) 2-stage process를 1-stage로 만드는 것을 목표로 합니다. 즉, correspondence를 설정하는 네트워크에 RANSAC-based PnP를 결합하여 네트워크 구조를 만드는 것입니다. PnP를 표준화 하는 접근 방식은 네트워크에 포함될 수 있지만, 수치에 대한 불안정성을 초래하는 SVD(Singular Value Decomposition)을 수행하기 때문에 무시할만한 문제는 아니라고 저자는 말합니다. 다른 연구에서는 SVD가 아닌 DLT(Direct Linear Transform)을 통해 PnP를 least-square 문제로 바꾸어 해당 문제를 해결하였지만, 해당 방법은 결과가 실제 회전에 대해 보장할 수 없고 추가적인 후처리가 여전히 필요합니다. 이와 대조적으로, 역전파에 친화적인 eigen decompostion 방법은 SVD를 수행하며, 원칙적으로 PnP를 수행하는 데 사용할 수 있습니다. 그러나 이렇게 하면 올바른 correspondence를 선택하기 위해 알고리즘의 RANSAC 부분을 고려하지 못합니다. RANSAC은 네트워크를 통해 얻을 수 있지만, 그림 1(b)에서 볼 수 있듯이 반복성이 낮기 때문에 end-to-end 6D pose estimation 네트워크를 학습하는 데는 적합하지 않습니다. 당시에 1-stage 6D pose estimation 네트워크를 설계하는 데 만족스러운 솔루션을 제안한 사람은 아무도 없으며, 이것이 바로 저자가 여기서 다루는 문제라고 합니다.

3. Approach

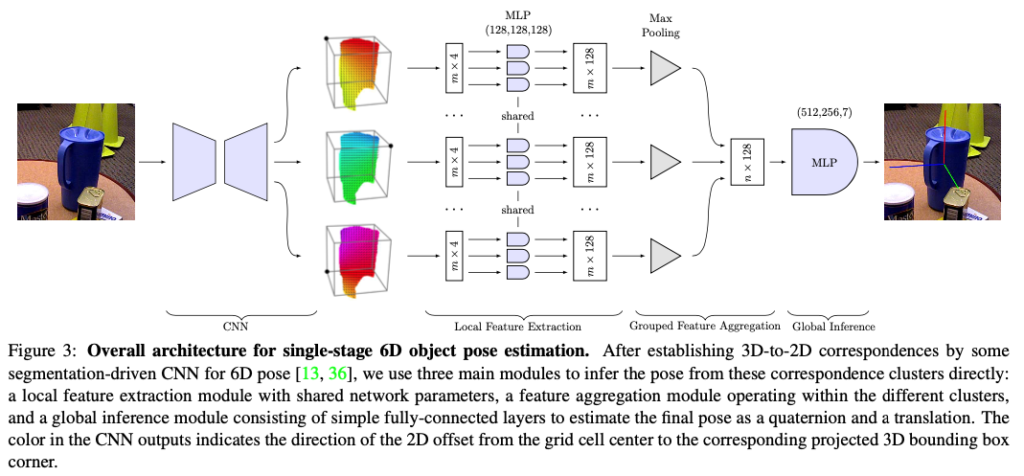
6D pose estimation의 목표는 Calibration된 카메라로 capture된 RGB 이미지가 주어졌을 때, 물체를 detection하고 pose를 추정하는 것입니다. 해당 task를 수행하기 위해서는 물체가 강체이고, 3D 모델을 사용할 수 있다고 가정이 되어야 합니다. 먼저 물체의 각 3D keypoint에 대해 2D correspondence 집합이 사전에 주어져 있다고 가정하고, 6D pose 문제를 formalize하고 이러한 입력으로부터 6D pose를 생성하는 네트워크 아키텍처를 제안합니다. 전체적인 프레임워크는 그림(3)과 같습니다.

3.1 6D Pose from Correspondence Clusters

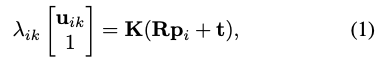
3×3 Camera intrinsic parameter K와 n개의 3D 오브젝트 keypoint p_{i} 각각에 대해 1≤i≤n, 1≤k≤m인 m개의 잠재적인 2D 대응값 u_{ik}가 주어졌을 때,

---

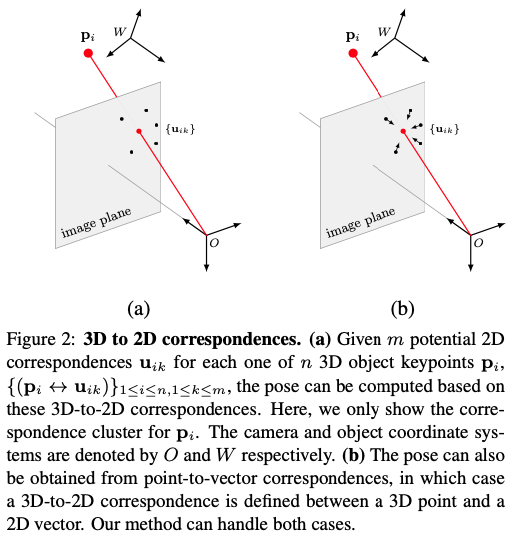
그림 2(a)와 같이 p_{i}는 object와 연결된 coordinate로 표현됩니다. 유효한 각 2D-3D correspondence p_{i} \leftrightarrow u_{ik}에 대해서 식(1)을 얻을 수 있고, 여기서 \lambda_{i}는 스케일 계수이고, R과 t는 camera pose를 정의하는 회전 행렬과 이동 벡터입니다. R은 회전이기 때문에 DoF(Degree of Freedom)가 3개만 있고, t도 DoF가 3개이므로 총 DoF는 6개입니다. 2D-3D correspondence는 2D-3D point correspondence에 국한되지 않습니다. 특히, 그림 2(b)에서 볼 수 있듯이, 3D point와 2D vector의 correspondence를 처리할 수 있습니다. 이는 네트워크와 함께 사용하기에 적합하다는 것이 증명이 되었고, 해당 방법을 사용하면 2D location은 두 2D vector의 교차점으로 유추할 수 있게 되면서, 식 (1)은 여전히 교차점에 대해 유지가 된다고 합니다. 아래에서 설명하는 접근 방식도 여전히 적용되므로 필요한 경우가 아니면 이 두 가지 유형의 2D-3D correspondence를 명시적으로 구분하지 않습니다. 고전적인 PnP 방법은 여러 개의 대응이 주어지면 R과 t를 복구하려고 시도하며, 일반적으로 유효한 대응을 찾기 위해 RANSAC을 사용합니다. 이 과정에서 유효한 대응만을 포함하는 대응을 찾기 전에 무작위로 선택된 많은 대응의 하위 집합에 대해 SVD를 수행해야 합니다.

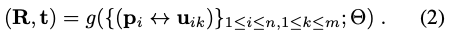
식(2)는 해당 논문에서 제안하는 위와 같이 번거로운 과정을 파라미터 \Theta를 사용하여 적절하게 설계된 네트워크인 g로 구현된 non-linear regression로 대체하는 식입니다. g_{\theta}을 어떻게 구현하는지 알아보도록 하겠습니다. C_{2}^{3}=\{(p_{i} \leftrightarrow u_{ik})\}를 의미합니다. 즉, 2D-3D correspondence 입니다.

3.1.1. Properties of the Correspondence Set

특정 3D-point에 연결된 모든 2D 포인트를 cluster 라고합니다. 그 이유는 이를 찾는 데 사용된 알고리즘이 좋은 알고리즘이라고 가정하면 그림(1)에서 볼 수 있듯이, 3D point projection의 실제 위치를 중심으로 클러스터링되는 경향이 있기 때문입니다. 이러한 구현 방식은 3가지의 고려사항이 있습니다.

Cluster ordering

cluster 내의 correspondence 순서는 관련이 없으며 결과에 영향을 미치지 않습니다. 그러나 cluster의 순서는 주어진 3D-point의 순서와 일치하며 고정되어 있습니다.

Interaction within a cluster and across clusters

동일한 cluster의 point가 동일한 3D-point에 해당하더라도 각 point에 대한 2D 위치 추정치는 noise가 있을 것으로 예상해야 합니다. 따라서 모델은 각 cluster 내의 noise distribution를 알아야 합니다. 더 중요한 것은 하나의 cluster만으로는 pose에 대해 아무것도 알 수 없으며, 전체구조에 대해 여러 cluster를 이용하여 최종 pose를 추정할 수 있다는 것입니다.

Rigid transformations matter

네트워크로 3D point cloud를 처리할 때는 일반적으로 결과가 invariant rigid transformation을 원합니다. 반면, 여기서는 2D-point가 3D-point의 projection으로 나타내기를 원하며, pose 추정에 중요한 절대적인 위치에 의존하지 않는 특징을 추출해야 합니다.

3.1.2. Network Architecture

correspondence cluster로부터 pose를 예측하는 네트워크 구조는 그림(3)과 같이 구성됩니다. 해당 아키텍처는 3가지 주요 모듈로 구성이 됩니다.

Local feature extraction

3개의 레이어로 구성된 shared-MLP를 사용하여 각 대응에 대한 local feature을 추출하면서 weight는 correspondence와 cluster 전체에 걸쳐서 공유합니다.

Grouped feature aggregation

cluster의 순서는 주어지지만 각 cluster 내의 point는 순서가 없으므로 각 클러스터에 대한 representation을 추출하기 위해 correspondence 순서에 민감하지 않은 그룹화된 특징 집계 방법을 설계합니다.

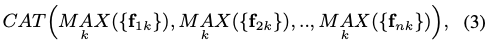
각각 m개의 2D-point \{u_{ik}\}{1 ≤ i ≤ n,1 ≤ k ≤ m}을 포함하는 n개의 cluster가 주어지면, 대응하는 \{u{ik}\}{1≤k≤m}을 nD-차원 벡터인 식(3)에 대해 mapping 하는 집합 함수 \mathcal F : \mathcal X → R^{nD}를 정의합니다. f{ik}는 앞서 언급한 FC layer를 통해 얻은 u_{ik}의 D차원 feature representation을 나타내고 MAX()는 max-pooling 및 CAT()는 concatenate입니다. 해당 모델에서는 실험을 통해 성능 향상이 되지 않았기 때문에 BN(Batch Normalization)을 사용하지 않았다고 합니다. 해당 논문의 official code가 생각보다 간단해서 분석하기 위해 shared-MLP를 어떻게 구현을 했는지 알아봤는데 conv1d를 사용하여 구현을 했고, 해당 식(3)처럼 Max-pooling과 concat을 하는 모습은 보이지 않고, 1d 연산을 하기 때문에(?) fc layer로 크기를 줄이는 식으로 사용을 하는 것을 확인할 수 있었습니다. 식(3)은 cluster 내의 모든 순열에 대해서는 invariant이지만 사전에 정의된 cluster 순서를 여전히 유지하므로 해당 방식의 이점에 대해 실험 section에서 해당 접근 방식의 이점을 설명하겠습니다.

Global inference

그룹 특징을 집계한 nD차원 벡터를 6D pose를 출력하는 또 다른 MLP로 전달합니다. 이를 위해 3개의 FC layer를 사용하고 최종 pose를 quaternion(rotation) 과 translation으로 encode하는 방식으로 진행합니다.

3.2. Single-Stage 6D Object Pose Estimation

위에서 설명한 네트워크는 주어진 물체에 대한 correspondence cluster로부터 6D pose를 예측할 수 있는 다양한 방법을 제공합니다. 따라서 입력 이미지가 주어지면 각 물체를 detect하고 2D-3D correspondence를 설정해야 합니다.

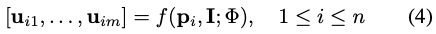
이를 위해 파라미터 \Phi가 있는 또 다른 regressor f를 사용하여 하나의 물체에 대해 식(4)를 얻을 수 있으며, 여기서 I는 입력 RGB 이미지입니다. f를 구현하기 위해 [13] 또는 [36]의 encoder-decoder 아키텍처를 사용했다고 합니다. 전체 아키텍처에서 CNN 파트라고 이해하시면 되겠습니다.

[13] Yinlin Hu, Joachim Hugonot, Pascal Fua, and Mathieu Salz- mann. Segmentation-Driven 6D Object Pose Estimation. In Conference on Computer Vision and Pattern Recognition, 2019.

[36] Sida Peng, Yuan Liu, Qixing Huang, Hujun Bao, and Xi- aowei Zhou. PVNet: Pixel-Wise Voting Network for 6DoF Pose Estimation. In Conference on Computer Vision and Pat- tern Recognition, 2019.

실제로 \{p_i\}는 물체에 대한 3D 모델의 3D bbox의 8개 모서리로 간주되는 경우가 많으므로 물체 유형에 따라 서로 다른 3D point \{p_i\}가 됩니다. 실험을 통해 모든 물체에 대해 동일한 \{p_i\}를 사용하면 f_{\phi}의 정확도에 거의 영향을 미치지 않으며 이후 g_\theta의 학습이 훨씬 쉽게 되는 것을 관찰했다고 합니다. 따라서 모든 데이터셋의 오브젝트에 대해 single cube를 사용하며, 반경이 모든 객체에 대한 3D 모델의 bounding spheres의 평균인 구에 포함된 가장 큰 cube로 정의됩니다. 즉, 3D 키포인트 좌표는 cluster의 순서에 따라 암시적으로 주어지며 네트워크 입력으로 명시적으로 지정할 필요가 없습니다. 따라서 각 input correspondence에 대해 3D 좌표가 포함되지 않은 4D representation을 사용합니다. 대신 [13]의 네트워크는 이미지 grid에서 작동하기 때문에 대응을 찾는 데 사용할 때 2D projection이 존재하는 grid cell 중심의 x, y 좌표와 해당 중심으로부터의 offset dx, dy을 입력으로 받습니다. 즉, 2D correspondence의 이미지 좌표는 x + dx 및 y + dy입니다. 대응을 찾기 위해 [13]의 네트워크 대신 [36]의 네트워크를 사용할 때는 동일한 입력 형식을 사용하지만 방향을 나타내도록 dx와 dy를 정규화합니다.

따라서 전체 모델은 식(5)와 같이 나타낼 수 있습니다.

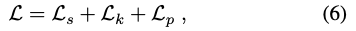
이를 학습하기 위해 각 grid cell을 배경의 객체 클래스에 할당하는 것을 목표로 하는 segmentation term \mathcal L_s, keypoint regression term \mathcal L_k, pose estimation term \mathcal L_p를 결합한 손실 함수 (6)를 최소화하도록 loss function을 설계했습니다. 두 아키텍처 중 어떤 것을 사용하느냐에 따라 \mathcal L_s를 focal loss로, \mathcal L_k를 [13] 또는 [36]의 regression term으로 취합니다.

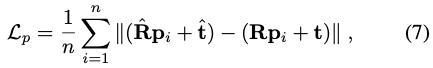
\mathcal L_p를 3D reconstruction error인 식(7)를 이용하고 여기서 \hat R 및 \hat t는 추정된 회전 행렬과 이동 벡터, R과 t는 GT입니다. 회전은 추정된 quaternion과 GT quaternion으로부터 추정되며, 이는 PnP 방식과 차별화 가능한 방식으로 수행될 수 있습니다. 또한 regression 대상이 모두 비슷한 범위를 갖도록 translation을 정규화합니다.

4. Experiments

해당 1-stage approach에서는 Synthetic data, LM-O, YCB-V에 대해 실험을 진행합니다.

4.1. Synthetic Data

image size 640 × 480, focal length 800, 이미지 중심에 principal point가 있는 가상의 calibrated camera를 사용하여 synthetic 2D-3D correspondences를 생성합니다.

그림(4)와 같이 target object를 임의로 회전하고 카메라 좌표계로 표현된 [-2, 2] × [-2, 2] × [4, 8] 범위 내에서 중심을 임의로 이동하는 단위 3D 구체를 설정합니다.

앞서 section 3.2에서 correspondence cluster에서 pose를 regression하는 네트워크인 g_{\theta}는 [x,y,dx,dy] 형식의 4D 입력을 기대하는데, 여기서 x,y는 이미지 그리드 위치의 중심을 나타내고 dx, dy는 offset을 의미합니다. 즉, 그 중심으로부터의 이동을 나타냅니다. 여기서 각각은 특정 객체에 대한 sphere bbox의 특정 모서리에 대한 잠재적인 이미지 대응을 나타내야 합니다.

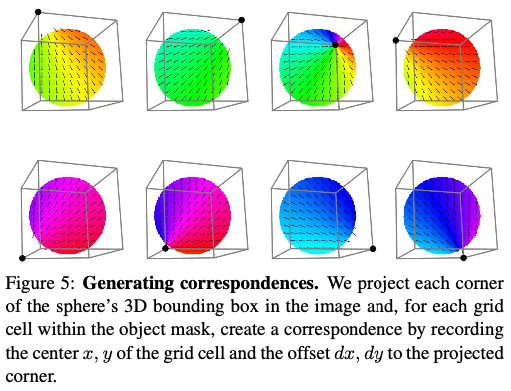
그림(5)는 이미지에 객체의 3D 모델을 projection하여 얻은 특정 객체의 segmetation mask가 주어지면 다음과 같은 방식으로 correspondence를 만드는 절차를 보여주는 그림입니다. sphere의 3D bbox의 각 모서리를 이미지에 projection하고, segmentation mask의 각 grid cell에 대해 cell의 중심 x, y와 projection된 모서리에 대한 변화량 dx, dy를 기록합니다. 그런 다음 mask 내에서 random sampling된 200개의 grid cell에서 결과 correspondence를 가져옵니다. 해당 결과값에 Gaussian noise를 추가하고 이미지에서 균일하게 sampling된 값에 대해 dx, dy의 일정 비율을 설정하여 이상값을 생성합니다.

Comparing with RANSAC PnP

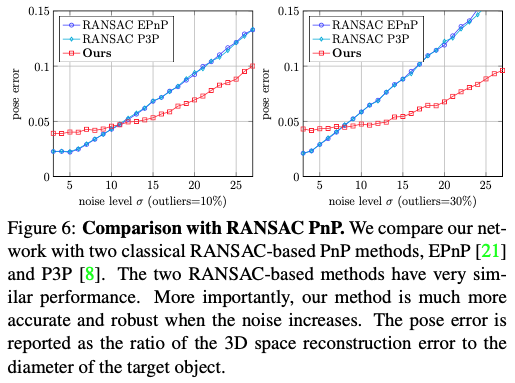
PnP 알고리즘과 RANSAC을 결합하는 것은 noise가 많은 correspondence를 처리하기 위한 가장 널리 사용되는 접근 방식입니다. 그림(6)은 RANSAC-based EPnP와 RANSAC-based P3P의 성능이 비슷하다는 것을 보여줍니다. noise가 거의 없을 때는 learning-based method보다 더 정확하지만, noise-level이 높아지면 learning-based method가 좀 더 정확해지는 것을 알 수 있습니다.

Importance of correspondence clustering

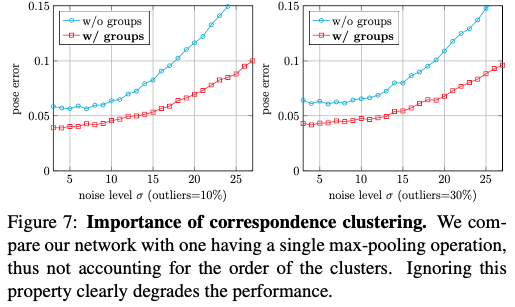
저자는 keypoint와 일치하는 cluster 순서를 고려하지 않고 모든 correspondence에 대해 permutation-invariant(순열 불변성)을 달성하기 위해 single max-pooling 연산을 사용하는 단순화된 버전을 구현하여 네트워크 구조의 중요성을 증명하기 위해 해당 실험을 진행하였는데요. 해당 실험을 수행하려면 각 correspondence에 연결된 3D keypoint 좌표를 네트워크에 입력으로 전달하기 위해 통합을 해야 했고, 그림(7)에서 볼 수 있듯이 keypoint의 고정 순서를 모델링하지 않으면 정확도가 크게 떨어집니다.

Comparing with PVNet’s voting-based PnP

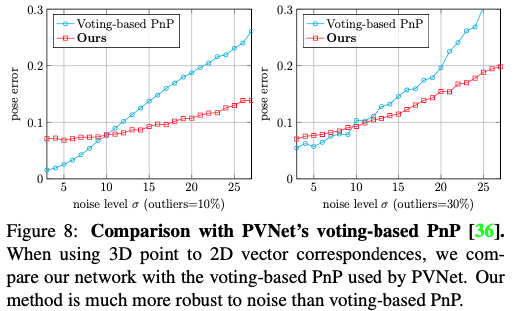
위의 실험에서 2D correspondence은 이미지 point의 2D location로 표현되었습니다. 당시 최신 방법론 중, 방향을 대신 사용하고 voting-based PnP 방식을 사용하여 pose를 추론하므로, 동일한 3D-point와 2D-vector correspondence를 자체 네트워크에 전달합니다. 이 설정에서는 그림(8)에서 볼 수 있듯이 pose가 correspondence noise에 더 민감합니다. 그러나 앞의 사례에서와 같이 noise가 적을 때는 voting-based PnP가 더 정확한 결과를 산출하지만, noise-level이 높아질 때는 저자가 제안한 방식이 정확한 결과를 보여줍니다.

4.2. Real Data

Metrics

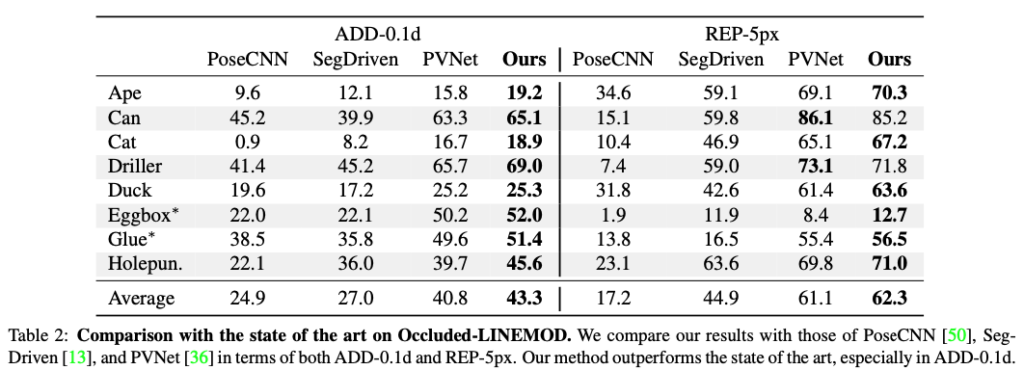
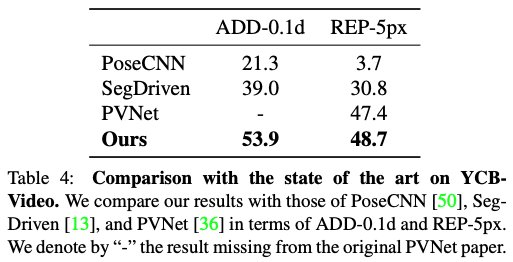
2D에서는 3D 모델의 point의 일반적인 2D reprojection error를 사용하며, 이를 REP라고 합니다. pose 정확도는 복구된 pose 중 올바른 pose의 비율로 측정합니다. 아래 표에서는 ADD가 모델 diameter의 10% 미만, REP가 5픽셀 미만이면 예측된 pose가 올바른 것으로 간주하는 ADD-0.1d 및 REP-5px를 각각 보고합니다. 각 metric에 대해 대칭 물체의 경우 대칭 버전을 사용하며, ∗ 위첨자로 표시합니다.

4.2.1 Occluded-LINEMOD Results

4.2.2 YCB-Video Results

4.3. Limitations

저자가 제안한 방법은 correspondence-extraction 네트워크인 [13, 36]와 함께 사용하면 정확하고 빠르지만, 그림(6)과 같이 다른 방법으로 매우 정확한 correspondence를 얻을 수 있는 경우 correspondence로부터 pose를 추정하는 네트워크는 여전히 기존의 geometry-based PnP 알고리즘만큼 정확하지 않습니다. 또한 고정된 3D 좌표 세트에 대해서만 학습했기 때문에 일반적인 PnP 문제를 해결하지 못합니다. 이 문제를 해결하는 것에 향후 연구의 초점이라고 합니다.

5. Conclusion

6D detection 및 pose estimation을 위한 1-stage 접근 방식을 도입했습니다.해당 접근법의 핵심 요소는 후보 2D-3D correspondence를 가져와 6D pose를 반환하는 간단한 네트워크입니다. correspondence를 설정하는 접근 방식과 결합하면 end-to-end 학습이 가능하고 일반적으로 필요한 번거로운 RANSAC 절차를 제거하여 성능을 향상시킬 수 있습니다.