안녕하세요. 열 여섯번째입니다. 금주는 이전 몇 번의 클러스터링을 활용한 object detection (UfpMp-det, clusDet) 리뷰 및 세미나를 진행하였으며 실제로 이를 pedestrian detection으로 확장하여 실험을 진행하는 도중 해당 아이디어를 적용하고자 읽은 논문입니다. 논문을 읽으며 오랜만에 저자의 고찰이 듬뿍 담긴 글임이 느껴져 재밌었네요. 사실 본 논문의 주 contribution은 익히 김태주 연구원님의 리뷰 및 세미나를 통해 또 Kaist leaderboard를 보며 알고 있었지만 전문을 읽어보지는 않았으므로 다음 주 실험에 적용하기 전 읽어보고자하는 마음으로 리뷰를 작성하게 되었습니다. 저자의 수학적인 고찰을 더 해석해보고 싶었지만, 제 수학적 지식의 부족함으로 이해에 도움이 안된 부분이 있다면, 미리 죄송합니다! 본 논문은 저자의 아이디어 및 고찰을 위주로 살펴보고자합니다. 어렵지 않고 대부분이 아는 내용 (NMS에 대한 설명, Fusion (Earlyway, Halfway, Lateway)에 대한 설명은 모두들 아는 내용이니 이에 대한 설명은 패스하겠습니다)이므로 읽기 어렵지 않을 것 같습니다. 그럼 시작하겠습니다.

Introduction

object detection, pedestrian detection이 자율주행차 (Autonomous Vehicles; AVs) 시스템의 핵심적인 부분이라는 점은 이견이 없습니다. 자율주행차의 실현을 위해서는 24시간 내내 환경에 영향받지 않는 객체 탐지를 필요로 합니다. 사실 LiDAR 등의 고급 장비를 활용한 연구들 (3D로 나아가는 추세에서는)이 활발해지는 것도 맞지만, 상용화의 관점에선 실현 가능성에 의문이 듭니다. 여튼, 최근 김남일 연구원님의 세미나에서 말씀하신 바처럼 object detection이 연구 및 실용화를 둘 다 잡고자한다면, 딥러닝이라는 측면 (data-driven)을 생각했을 때 연구실에서 “dark data”라고 불리는 빅데이터적인 시야에서의 detection을 엮은 태스크 관심이 있습니다.

Multimodal Data and Multimodal Fusion

다시 논문으로 돌아와 RGB, thermal 중 후자가 저조도 환경에서 RGB에 비해 강인함을 보이는 것 또한 이제는 이견이 없습니다. 물론 열 방출이나 열 반사를 하지 않고 열을 흡수하는 객체라면 이에 대해서는 다시 연구가 필요하겠지만, 결과적으로 모든 Multispectral 논문에서는 RGB, thermal 두 모달리티의 각 장점 및 단점을 설명하고 이를 상호보완적으로 활용하고자하는 연구가 주류를 이루고 있었습니다. Kaist dataset이나 FLIR dataset이 Multispectral 이미지를 Annotation한 대표적인 데이터 셋이지만 우선 FLIR dataset의 단점을 살펴보겠습니다. 사실 두 데이터 셋은 2023년에서 바라보면 예전 데이터이긴 합니다. Pixel resolution을 생각했을 때도 지금과는 약 2배 이상 차이나는데, Multispectral dataset을 구성하는 것은 사실 쉬운 일이 아닙니다.

위에서 쉬운 일이 아니라고 하는 것에 대해 우리는 익히 알고 있습니다. 만약 10,000장의 영상을 촬영했다고 할 때, RGB와 thermal의 alignment가 정확히 일치한다면, 하나의 Annotation만 있으면 되겠죠. 하지만 아래 Fig. 4의 FLIR dataset과 같이 광학적 중심을 일치하지 않았거나, Sycnhronization을 맞추지 않았거나, stereo camera calibration 과정을 거치지 않았다면 보이는 바와 같이 두 영상에 Annotation이 따로 적용되어야합니다. 10,000장의 영상을 촬영했다고하니, 20,000번의 Annotation이 필요하겠네요. 그렇다면 Kaist dataset은 alignment가 정확히 일치하나요? 사실 이에 대해 웬만하면 아시겠지만, 그렇지 않습니다. 광학적 중심을 일치하고자 Beam spliter 등을 활용하고 이외 Sync를 맞추는 작업이 있었을 것이라 예상함에도 사실 세상에 100%는 존재하지 않듯 이는 실제로 불가능의 영역에 가깝습니다. 전기적 신호를 통해 영상 촬영을 한다한들, 오차는 존재할 수 있습니다.

저자는 Multimodal(Multispectral) 영상의 alignemnet가 맞지 않는 상황에 대한 연구는 활발히 진행되고 있지 않음을 언급하며 현존 데이터 셋들은 Annotation 시 어느 한 영상을 기준으로 설정하기 때문에 기존 Multimodal learning 방식이 과연 옳을까를 고찰하고 있는 것으로 보입니다. 이를 정리하면, 대표적으로 Alignment 문제를 언급하며 Multimodal의 정보를 영상에서 전달하는, 또는 모델에서 병합하는 방식이 과연 정말 나아가야할 방향인지에 대해 의문점을 품습니다.

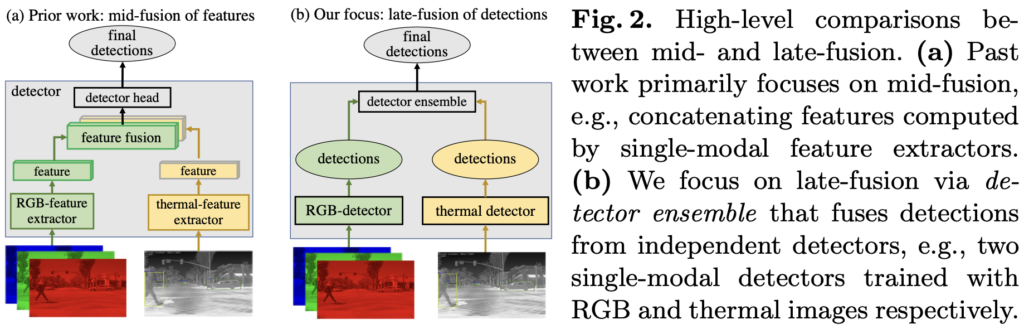
Multimodal Fusion이 대표적인 예시입니다. Fusion이란 의미대로 연구의 주요 관점은 다른 Modality의 정보를 융합하는 것에 이목이 있었습니다. 이 때 우리가 익숙한 Early, Mid(Half), Late Fusion이 등장하며 각 이점은 다르지만, 이런 연구들은 결국 어디서, 어떤 방식으로 정보를 결합하는 지에 관심이 있습니다. 이는 두 Modality의 이점을 딥러닝 모델이 어떻게 활용할 것인가의 측면이지만, 저자는 이 방법이 아닌 very-Late Fusion이라는 이름을 붙이며 각 Modality의 특성은 최대한 활용한 채 detector를 Fusion하는 방식을 취합니다. 아래 Fig. 2를 살펴보면, 단번에 이해됩니다.

Probabilistic Ensembling (ProbEn)

확률적 앙상블 (ProbEn)이란 위에서 언급한 바처럼 RGB, thermal, 만약 또 다른 Modality가 있다고 한다면 (예를 들면 LiDAR도 활용 가능하겠네요) 하나의 전제되는 가정이 필요합니다. 사실 필요한다기 보단 아이디어 자체가 이를 만족한다고 볼 수 있는데 바로 조건부 독립, 쉽게 말해서 두 사건은 독립 사건이여야한다는 점입니다. 이는 Modality의 Feature를 Fusion하는 Fig. 2의 (a)는 만족할 수 없습니다. 두 사건이 독립이라함이 만족되지 않는다는 것인데, 예를 들어 사람을 찾았다할지언정 이 정보가 RGB로부터 기인할 수 있었던 것인지, thermal로부터 기인할 수 있었던 것인지는 단정할 수 없습니다. 물론 혹자는 ‘그럼 어때, 결국 두 정보를 융합하여 잘 찾았으니 괜찮지’라고 말할 수 있지만, 두 사건이 독립이라면 Modality 별 classification score, bounding box offset을 확률로 접근할 수 있고 동시에 두 사건이 독립임을 만족한다는 것을 확장하여 우리는 베이즈 정리를 활용하여 최적의 Fusion 방법을 구성할 수 있습니다. 사실 저자의 내포된 의미는 이전 Fusion 방법론은 진정한 Information Fusion이라고 보기에 한계가 있다는 것을 시사합니다. Fusion 이후 통합된 detector를 통과할텐데, 결국 detector라 함은 black-box이므로 확률적, 수학적 접근을 사용하기 어렵게 되기 때문이죠.

Why ensemble?

그렇다면 왜 Ensembling이란 표현을 사용하나요? 저자의 의도는 결국 “RGB, thermal의 두 Modality가 상호 간 정보를 보완해주어 단점이 아닌 장점만을 가져온다면 모델의 성능이 올라감은 분명할 것이다.”는 대전제를 기반합니다. 단점을 극복하고자 한 하나의 방법이 대표적으로는 Halfway Fusion 방식일 것 입니다. 이는 Model 측면에서 해결하고자한 방면으로, 좋은 말로 포장한다면 “RGB, thermal의 두 정보를 학습함과 동시에 모델이 어느정도 학습한 이후에는 상호보완적으로 학습하고자 단순히 합쳐서 학습해보자”는 의미입니다. 사실 위의 몇 문단동안 모두가 아는 내용을 재차 언급하고 있지만, 우리가 실제 Halfway Fusion을 받아들였을 때도 이에 대해 장점만을 생각하다보니 비판적인 시각을 갖지 못하지는 않았을까 생각합니다. 또한 마치 발명과 같이 완전히 새로운 것이 아닌 “알고 있는 것으로부터 개선점을 찾아 새로운 것을 만들어나갈 수 있는 능력”또한 중요한 것 같네요.

저자의 의도는, Feature Fusion은 Modality에서 검출하지 못한 “missing”의 것들에 대해서는 다루지 않고 있다고 합니다. 이를 “missing” modality로 표현하는데, 즉 Feature Fusion 시에는 Fusion 이전 RGB 또는 thermal Modality에서 찾지 못했다면 Fusion 시에도 큰 이점을 보일지는 의문이라고 말합니다. 그렇죠, 충분히 납득됩니다. 우리는 RGB에서 못찾은 객체는 thermal에서 잘 찾을 수 있다는 대전제가 있음에도 과연 모델 학습 중 Feature를 Fusion함으로써 이를 해결할 수 있을 것이라는 막연한 기대감이였을 뿐, 직관적으로 “왜” 그런지는 잘 보이지 않았습니다.

Fusion Strategies for Mutimodal Detection

ProbEn의 과정을 담은 알고리즘입니다. ProbEn을 NMS와 비교하는데, NMS는 익히 알고 있으니 넘어가며 둘 다 예측 detection 결과와 GT 간 threshold를 넘는 예측에 대해 다룹니다. ProbEn은 NMS와 달리 T, 즉 각 Modality에서 가장 높은 score를 갖는 결과끼리 Eq. (4)와 Eq. (8)의 연산을 통해 계산합니다. 그럼 핵심인 Eq. (4)와 (8)을 봐야하는데, 이것이 베이즈 정리에 기반하고 있음을 알면 어렵지 않습니다. 그 이유와 베이즈 정리를 사용할 수 있는 이유에 대해서도 이미 언급했습니다.

Naive Pooling, NMS and Average Fusion

NMS와 비교한 이유는 NMS는 단순히 detection의 결과 중 더 높은 score를 갖는 결과만을 가지고, 나머지를 suppression하기 때문입니다. 즉, MultiModality detector의 서로의 결과를 적응적으로 잘 활용하지는 못합니다. 이를 저자는 원문에서 다음과 같이 말합니다. “NMS fails to “fuse” information from multiple modalities together.”

물론 이전에도 Fusion 중 detector의 결과를 Fusion하고자한 시도가 아예 없었던 것은 아닙니다. 모두들 알고 있는 Average Fusion입니다. 이 방법은 Modality detection의 결과를 단순히 평균내는 방식을 취하지만, 이는 NMS score를 필연적으로 낮추게 됩니다. 사실 NMS 이후 나온 방법인데, 당연하게 두 score가 낮아질 수 있음이 보이는데 왜 이런 방식을 채택했을 지는 잘 모르겠습니다. 그럼 Fig. 1을 통해 앞선 두 NMS와 Average Fusion을 담은 본 논문의 대표적인 사진을 보고서, ProbEN의 수식에 대해 알아보겠습니다. 이 때 (a) Pooling은 단순한 방식의, Naive Pooling으로 두 결과를 합치는 방식이지만 중복된 결과를 낸다는 점에서 유의미하진 않습니다.

Probabilistic Ensembling (ProbEn)

대전제인 Modality들이 조건부 독립 (독립 사건)이라는 사실은 아래 (1)로 표현할 수 있습니다. 이 때 x_1, x_2, y 는 각각 RGB, thermal에서의 예측과 GT를 의미합니다.

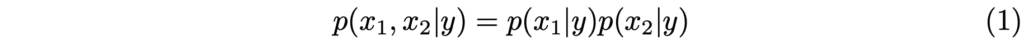
살펴보면 Eq. (1)을 p(x_1 | y) = p(x_1 | x_2, y) 로 표현해도 무방합니다. 즉, x_2 의 확률이 x_1 의 확률에 영향을 주지 않음을, 조건부 독립인 상황임을 의미합니다. Eq. (1)이 의미하는 바는 GT y가 주어졌을 때 각 Modality가 예측하는 확률을 의미하며 앞으로 말하는 확률이라함은, 쉽게 이해하고자 한다면 Fig. 1의 bounding box 위 classification score를 떠올리면 됩니다.

실은 GT y가 주어졌을 때의 모델의 확률은 큰 의미를 보이지 않고, 실제로는 모델이 예측했을 때 해당 예측이 GT y일 확률을 구하는 것이 중요합니다. Eq. (1)을 활용하여 이를 설계한 식이 Eq. (2)입니다. 이 때 수식의 단순함을 위하여, 상수 취급할 수 있는 p(x_1, x_2) 를 무시한 근사로 식을 구성했습니다.

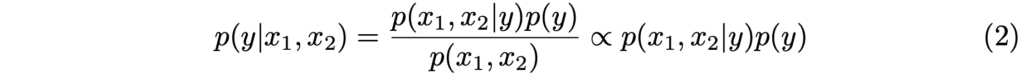
조건부 독립 가정을 Eq. (1)로부터 Eq. (2)로 적용하면, 즉 두 수식을 토대로 베이즈 정리를 활용하면 Eq. (3)과 (4)로 표현할 수 있습니다. 이 때 Eq. (4)는 Eq. (3)을 정리한 것에 불과합니다. 물론 베이즈 정리가 ProbEn에 적용된 수학적인 핵심 개념이며 확률에서 굉장히 중요하지만, 이에 대해 설명하면 리뷰의 본질을 벗어나는 것 같아 짧게만 설명하고 넘어가겠습니다.

베이즈 정리란, 즉 조건부 독립 가정이란 확률 변수 A, B가 주어지고 C가 주어진 상황에서 서로 독립적으로 발생한다는 것을 보이는 것으로, P(A, B | C) = P(A | C) \cdot P(B | C) 으로 정의내릴 수 있습니다. 구글링을 통해 실 생활에서의 예시를 찾아보니 좋은 설명이 있어 인용하자면, 베이즈 정리는 어떤 사전지식이 있을 때 이 지식을 이용해 관심있는 사건이 일어날 확률을 구하는데 사용되며 예를 들어 ‘당뇨병 발생률은 10%’와 ‘당뇨 진단 정확률 95%’라는 사전지식이 있다면, ‘당뇨로 진단 받은 환자가 실제 당뇨일 확률’을 알 수 있다는 내용입니다.

이를 pedestrian detection에서는 RGB Modality에서의 확률과 thermal Modality에서의 확률이 있다면, 영상 내 예측이 실제 GT일 확률을 구할 수 있다로 귀결될 수 있겠네요. 즉, 두 Modality가 독립 사건이기 때문에 두 확률을 통해 GT일 확률로 접근할 수 있음을 시사합니다.

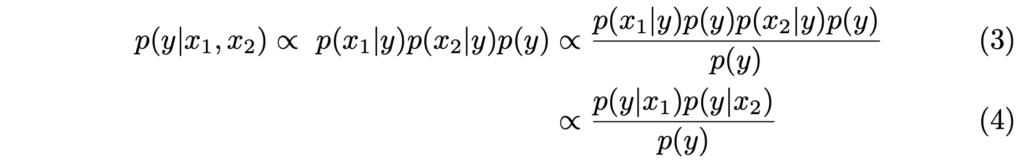
이 때 관심여겨볼 점은 p(y)를 구하는 방식인데, p(y)는 GT y일 확률을 구해야하나 우리는 이를 모르기에, 저자는 class prior인 p(y)를 클래스에 따라 Modality의 예측을 정규화하여 활용하는 방식을 채택했습니다. 이제 Eq. (4)를 일반화한 Eq. (5)를 보이며 저자는 결국 2개의 Modality 뿐만 아니라 몇 개의 Modality에 대해서도 “독립 사건”임을 만족한다면 이를 모두 활용할 수 있음을 말하고자 합니다.

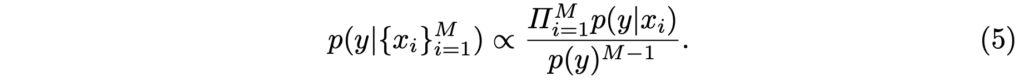
마지막으로는, logit score( s_i[k] )를 활용한 수식인 Eq. 6을 보입니다. 이는 이전의 다른 연구에서도 충분히 활용할 수 있음을, 즉 확률이라는 관점과 딥러닝을 연관했을 때 위 Eq. (4)를 어떻게든 변형하여 활용할 수 있음을 나타냅니다. 물론, 처음의 알고리즘에서 살펴봤듯 저자는 Eq. (4)를 통해 score를 계산합니다.

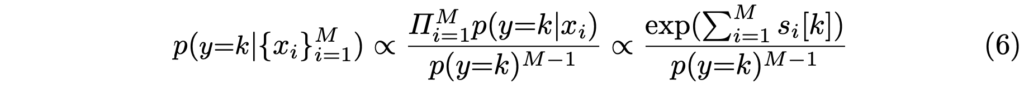
Independence assumptions and Missing modalities

간단히 짚고 넘어갈 점으로, 저자는 이처럼 조건부 독립인 Modality에 대해 ProbEn을 적용하는 것이 효과적임을 실험을 통해 보인다고 했지만, ProbEn 자체가 두 Modality의 예측을 Gaussian처럼 만드는, 즉 곱해주고 나눠주어 Normalize해주는 과정으로 인해 실제 독립이 아닌 경우에도 딥러닝 측면에서 적용할 수는 있으며 이 때도 성능이 높아짐에 대해 언급합니다. 사실 저자는 한 논문을 인용하며 앞서 언급한 NMS와 Average Fusion 또한 이러한 독립 사건의 가정이 내포되어 있음을 말하지만, 그보다 특히나 Average Fusion의 경우 어떤 Modality의 missing case에 대해 대처하기 쉽지 않기 때문에 더욱 Strict한 가정이 내제되어 있음을 언급하며, 자신들의 가정이 단지 수학적인 이론에 그치지 않음을 주장합니다.

마찬가지로 그렇다면 ProbEn이 좋은 성능을 보일 수 있음에 대해 저자는 missing modality를 다시 언급하며, ProbEn이 single-modal의 사후 확률인 p(y|x_1) 에 비해 확률적으로 표준화된 p(y|x_1, x_2) , 즉 Multi-Modality의 확률을 둘 다 다루고 있기에 성능이 좋을 수 있음을 언급합니다. 놀랍게도 본 contribution (ProbEn)이 딥러닝 모델을 건드리지 않고 있기 때문인지, 굉장히 수학적인 고찰이네요. missing modality에 대한 결과는 Fig. 3을 통해 미리 살펴보죠.

Bounding Box Fusion

이제 class score에 대한 ProbEn이 마쳤다면, 마지막으로는 Bounding Box에 대한 ProbEn이 남아있습니다. Bounding Box는 class score와는 달리 확률로 나타내기엔 까다로우며 따라서 만약 두 Modality에서의 Bounding Box 중 어떤 Bounding Box가 확률이 더 높은지, 낮은지를 따지는 것은 어렵습니다. 그러므로 저자는 세 방법을 실험적으로 결정하는데, 말하는 세 방법은 모두 Bounding Box의 불확실성에 대한 확률의 의미를 내포합니다.

이들은 수학적으로 쉽지 않은데, centroid, width, height로 연속 확률 변수인 z를 정의하고, p(z|x_i) 를 Gaussian 형태 ( p(z|x_i) = \mathcal{N}(\mu_i, \sigma^2_i I))를 따르도록 정의합니다. 이 때 \mathcal{N}(\mu_i, \sigma^2_i I)에서 \mu_i 는 i Modality로부터 예측된 Bounding Box의 좌표를, \sigma^2_i 는 i Modality에서의 Bounding Box의 분산을 의미합니다.

세 방법을 소개하기 전 결국 저자가 택한 마지막 방법인 “v-avg”는 GNLL (Gausian negative log likelihood) loss로부터 분산을 불확실성으로 나누어 예측하는 방식이며, Eq. (7), (8)의 수식을 통해 정의됩니다. 사실 이 부분은.. GNLL을 정확히 이해 못해서인지는 모르겠지만 수학적으로 해석하기 어렵습니다. 참고로 세 방법 중 두 방법은 “avg”와 “s-avg”로, 각각 분산을 1로 고정했을 때의 결과와 분산을 detection class score에 근사하여 더 높은 class score를 갖는 Bounding Box가 Fusion 시 더 중요하게 여겨지게끔 가중치를 주는 방식입니다. 앞서 말한 바와 같이 세 번째 방법을 택한 이유 또한 모두 실험을 통해 증명되었습니다. 이에 대해 새로운 고찰점을 가진다면, 즉 Bounding Box를 수학적으로 불확실성 이외 다른 측면으로 접근하여 확률을 엮을 수 있다면 더 좋은 성능을 보일 수 있을지도 궁금합니다.

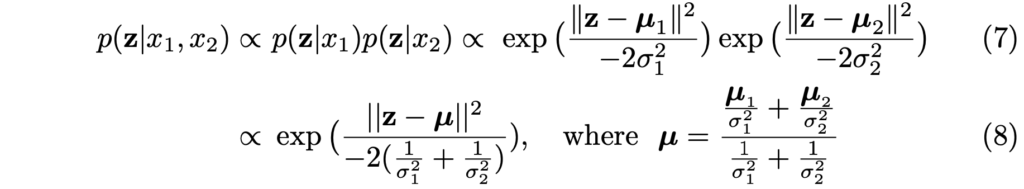
Experiments

앞서 말한것과 같이, 실험은 Multimodal dataset인 KAIST와 FLIR dataset에서 진행하였습니다. Pretrained weight를 사용하기 위해 thermal 이미지의 mean value를 계산하여 (135.438) mean subtraction으로 정규화해준 과정이 있으며, detector는 Faster-RCNN을 사용했습니다. 우선 실험은 정성적 자료가 눈에 띌 수 있을테니, Halfway(Mid) Fusion을 비교한 Fig. 5를 살펴보겠습니다.

위의 Fig. 5를 살펴보면, 초록, 빨강, 파랑 Bounding Box는 각각 TP, FN, FP를 보여주며 이 때 FN이 곧 miss-detection, 한 Modality에서 검출하지 못한 object를 ProbEn을 통해 검출했냐를 살펴봐야할 것 같습니다. 사실 정섲억 결과의 파란색을 제외한 Bounding Box만 살펴봐도, ProbEn을 통해 훨씬 많은 Pedestrian을 검출하고 있음을 알 수 있습니다. 이제 정량적 결과를 살펴보죠.

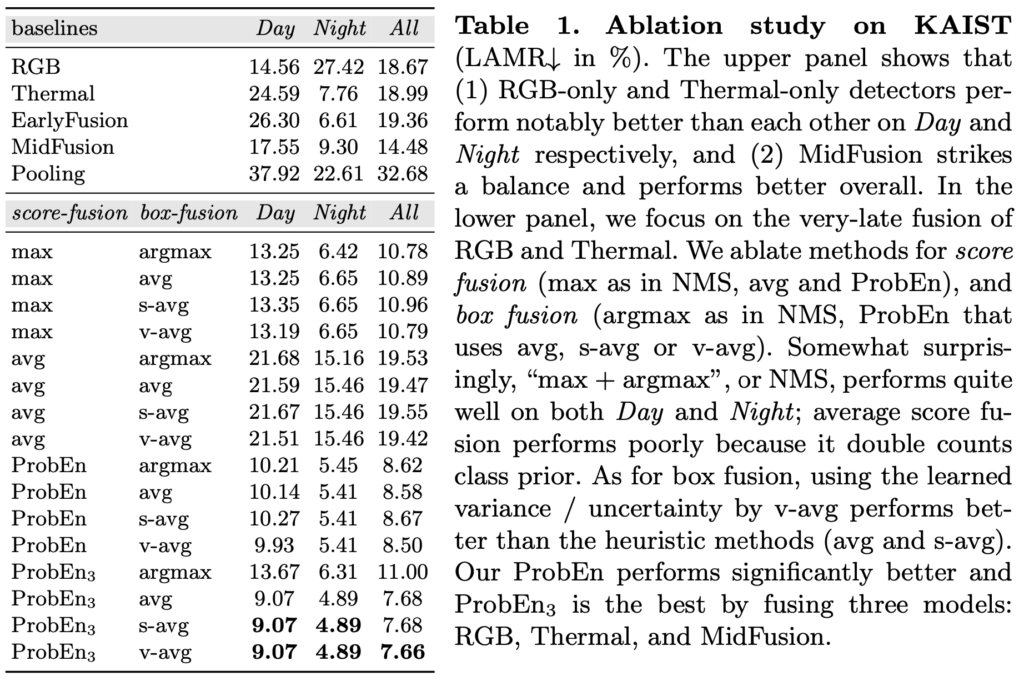
Faster RCNN 기반이여서인지, KAIST dataset에서 Baseline의 RGB와 Thermal의 성능 자체가 높은 것이 인상적이네요. 이 때 score-fusion과 box-fusion 방식에 따른 Ablation study를 살펴보면, max, avg는 각각 NMS와 Average Fusion을 의미하며 box-fusion의 avg, s-avg, v-avg는 앞서 설명한 불확실성을 고려한 세 Fusion 방식입니다. argmax는 NMS와 같음을 고려할 떄, score-fusion과 box-fusion이 max, argmax인 NMS만을 사용한 detector fusion 방식 자체도 All MR이 많이 낮으며, 저자가 실험적으로 보이자고한 ProbEn3와 avg, s-avg, v-avg를 살펴보면 최대 7.66의 MR를 내고 있음이 보입니다.

흥미로운 점으로, ProbEn3은 RGB, Thermal, MidFusion을 모두 합친 방식인데, 이 때 세 Modality가 상호 독립적인 관계를 만족할 수 있습니다. MidFusion 자체로는 RGB, Thermal의 독립성이 만족되지 않지만, MidFusion 그대로를 detector fusion을 통해 독립성을 만족시킬 수 있었다는 점이죠.

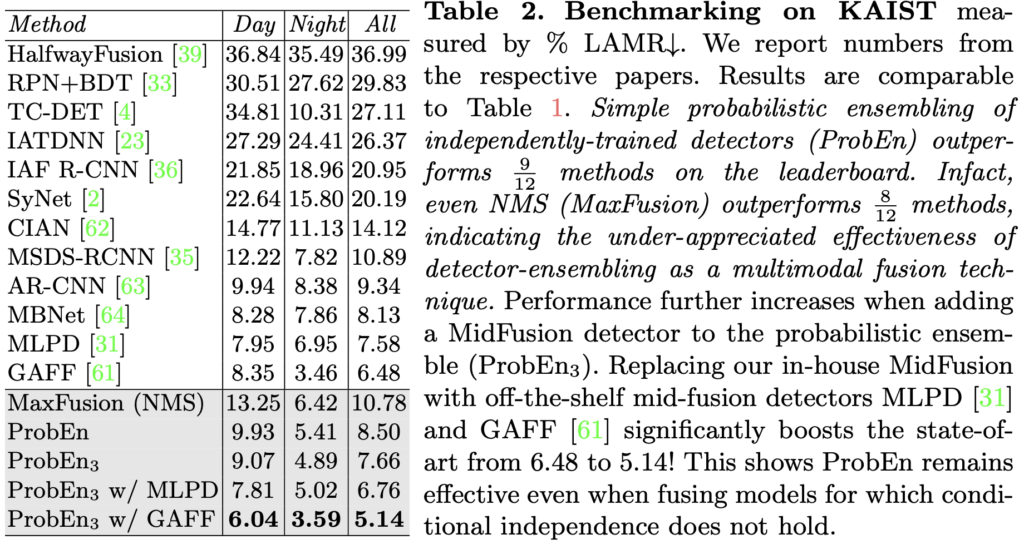
이를 KAIST dataset에서 기존 SoTA 방법론에 적용한 모습을 보아, MLPD, GAFF가 각각 7.58, 6.48의 MR에서 ProbEn3를 적용하면서 6.76, 5.14로 성능이 좋아진 것을 통해 저자는 “학습하지 않는, 모델 학습 이후의 수학적 방법을 통해서도 유의미한 성과를 보일 수 있음”을 보이고자 함이 아닐까 생각합니다. 이제 FLIR에서의 Ablation study를 살펴본 후, 마무리하겠습니다.

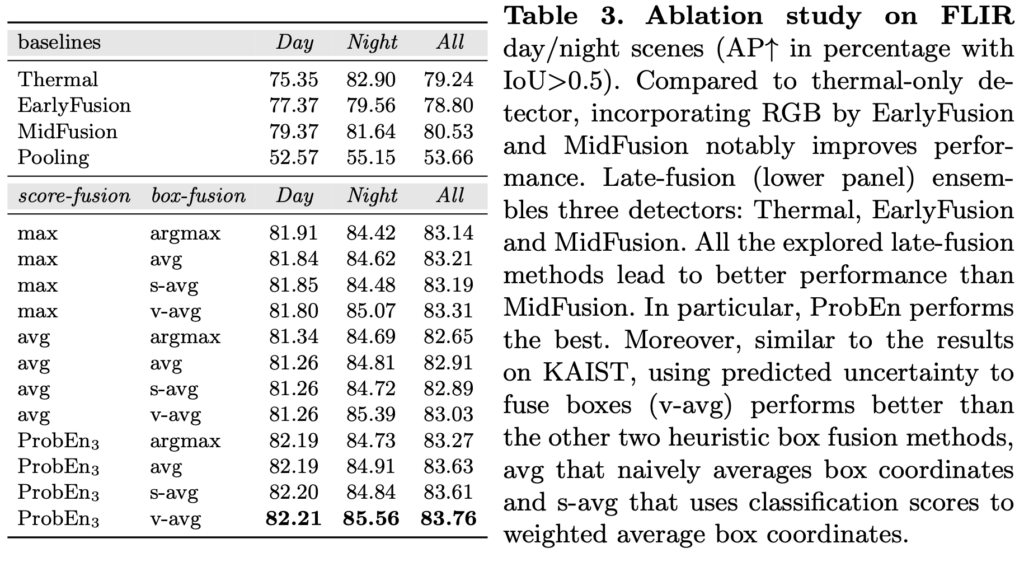
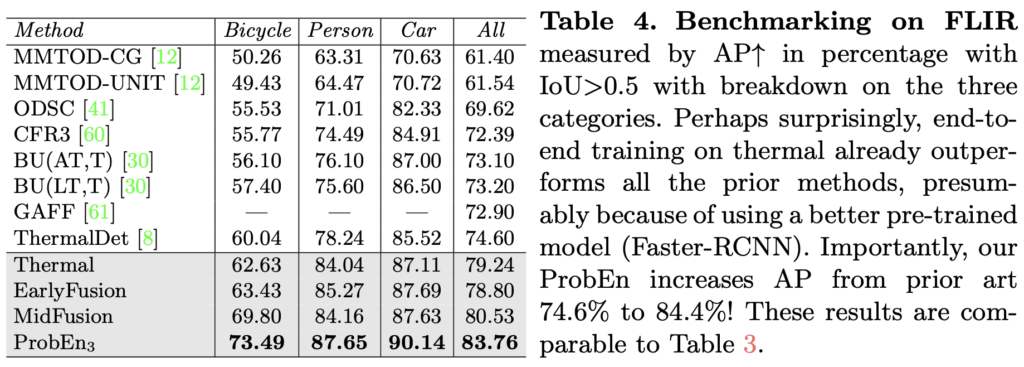
AP로 평가하는 FLIR에서도 KAIST와 동일한 세팅 (Baseline에 대한 ProbEn 성능 검증, SoTA 모델에 적용했을 때의 성능 검증)으로 실험했을 때 유의미한 결과를 보임을 알 수 있습니다. AP 측면에서는 어쩌면 KAIST에서보다 훨씬 높은 성능 향상을 보입니다. 또한, FLIR은 RGB와 thermal의 misalignment가 많은 dataset임에도 불구하고 성능 향상을 통해 저자가 일전에 말한 “ProbEn은 misalignment 상황에서도 효과적으로 작동할 수 있음”을 실험을 통해 보이고 있습니다.

마지막으로 FLIR에서의 정성적 결과도 살펴보며 마치겠습니다. 설명은 위의 KAIST에서와 동일하며, 무엇보다 ProbEn이 단순히봐도 “더 많이 찾는다”는 관점에서도 확률적 개념이 합당하게 사용될 수 있음을 보입니다. 어렵지는 않아서, 코드를 살펴보면 금방 적용할 수 있을 것으로 보이네요. 내일엔 아마 ProbEn을 통해 클러스터링 이미지를 합치는 방식을 구현해볼 예정입니다. 감사합니다.