[ECCV 2022] FCAF3D: Fully Convolutional Anchor-Free 3D Object Detection

안녕하세요, 일곱번째 엑스리뷰 입니다. 이번 리뷰는 처음으로 3D Object Detection에서 anchor-free 방식을 제안한 논문인 FCAF3D 입니다. 그럼 바로 리뷰 시작하겠습니다 !

1. Introdcution

Convolutional 3D object detection 방법론들은 공통적으로 scalability 문제가 존재하는데, scalability 문제라고 함은 큰 규모의 scene dataset은 point를 처리하는데 오랜 시간이 걸리고 많은 computational resource를 요구하게 됩니다. 기존 연구는 이러한 문제를 해결하기 위해서 point를 voxel data로 변환하고 sparse convolution을 적용하였습니다. 그러나 이러한 방법론들에 대해 저자는 scalability를 해결할 순 있겠지만 그에 따른 검출 accuracy가 하락하게 된다고 말합니다. 즉 3D Object Detection에서 scalability와 accuray를 함께 향상시킬 수 있는 방법론은 아직 존재하지 않는다는 것 입니다. 3D Object Detection에서는 3D bounding box의 aspect ratio와 size를 미리 정해놓음으로써 그에 따라 물체를 검출하게 되죠. 그러나 2D detection과 비슷한 맥락으로 미리 물체를 검출하기 위한 박스의 비율과 크기를 정해놓는 것은 물체에 대한 일반성을 떨어뜨리고 사전에 설정해야하는 하이퍼파라미터와 학습하기 위한 파라미터의 수가 늘어난다고 합니다. 그렇기에 저자는 이러한 미리 정해놓아야 하는 bounding box를 사용하지 않고 온전히 data에 기반한 3D에서의 anchor free 방식을 처음으로 제안하게 됩니다. 또한 기존 bounding box를 예측하는 방식에서 지적한 하이퍼파라미터 수의 증가한다는 문제를 해결하기 위해서 새로운 OBB parameterization을 추가적으로 제시합니다. 즉 본 논문의 main contribution을 정리하면 다음과 같습니다.

1. 최초로 indoor scene에 대한 3D Object Detection에서 anchor-free 방법론 FCAF3D 제안
2. 새로운 OBB parameterization 제안
3. ScanNet, SUN RGB-D, S3DIS 3개의 large-scale indoor dataset에서 SOTA 달성

2. Related work

3D Convolutional methods

Voxel 기반 3D Object detection 방법론은 point cloud를 voxel 형태로 변환 후 3D Convolutional network를 거치는 것이 일반적 입니다. 그러나 voxel을 처리하는 것은 많은 메모리와 계산비용을 요구하게 됩니다. GSDN은 그래서 이러한 이슈를 해결하기 위해 encoder-decoder 구조를 sparse 3D convolutional block으로 구성하였습니다. sparse 3D Convolution이란 convolution을 태우는 대상이 모든 voxel이 아니라 0이 아닌 값만을 input으로 convolution을 거치는 것을 의미합니다. 이를 통해 GSDN은 상당한 메모리 감소와 large scene에서의 scalabality를 유지할 수 있었는데 문제는 introduction에서도 언급하였듯이 accuracy가 낮다는 것 입니다. 결국 anchor-based 방식인 GSDN이 scalability를 해결하였다고 판단되니 이를 기반으로 anchor-free 방식을 도입함으로써 accuracy까지 향상시키겠다는 것이 저자가 Related work를 통해 하고자하는 이야기인 것 같습니다.

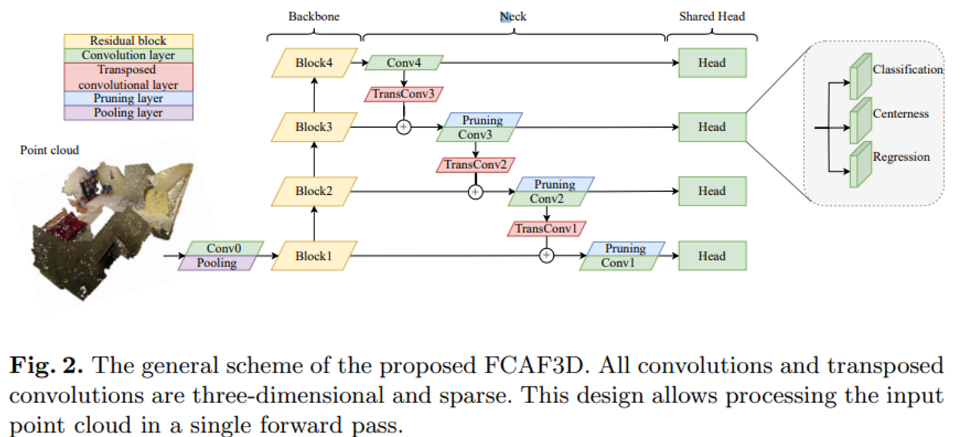
3. Proposed Method

FCAF3D는 N_{pts}개의 point를 입력으로 받아 3D Object bounding box를 output으로 출력하는 backbone-neck-head로 구성되어 있습니다.

3.1 Sparse Neural Network

먼저 Backbone은 ResNet의 2D Convolution을 sparse 3D Convolution으로 대체하여 HDResNet이라고 정의한 네트워크를 사용합니다. Backbone 다음의 Neck은 GSDN의 decoder을 간단하게 변형한 구조를 사용하였다고 합니다. Neck의 각 레벨에서 feature는 하나의 sparse transposed 3D convolution과 하나의 sparse 3D convolution을 거치게 되는데, 그 중 transposed 3D convolution은 커널 사이즈를 2로 가져 한번 convlution을 진행하면 0이 아닌 값이 8배로 급격하게 증가합니다. 이로 인한 메모리 증가를 방지하기 위하여 원래 GSDN은 probability masking을 통해 데이터를 필터링하는 pruning layer을 사용하였습니다. GSDN은 feature level-wise 확률을 scoring layer라는 convolution layer를 통해서 구하였지만, 본 논문에서는 scoring layer을 사용하지 않는 대신 Neck 다음의 head에서 classification layer을 거쳐 확률값을 얻습니다. GSDN은 확률 threshold를 지정하여 많은 voxel을 없애지만 FCAF3D에서는 input point N_{pts}개와 동일한 수의 voxel N_{vox}을 가지기 위해서 threshold를 조정하지 않습니다. 이러한 방식은 같은 하이퍼파라미터를 계속 사용하기 때문에 sparsity가 증가하는 것을 간단하게 방지할 수 있다고 합니다. 다음으로 Head는 feature level 사이에 공유된 가중치를 가지는 병렬적인 3개의 sparse convolution layer로 이루어져 있습니다. voxel의 각 (\hat{x}, \hat{y}, \hat{z}) 위치마다 head를 거치고 나면 classification score \hat{p}와 bounding box regression 파라미터 \delta, 마지막으로 centerness \hat{c}를 output으로 출력합니다.

다음과 같은 구조를 가진 FCAF3D는 학습 과정에서 위에서 언급한 location (\hat{x}, \hat{y}, \hat{z})에 각 feature level k \in \{1, 2, 3, 4\}가 추가된 location \{r_i = (\hat{x}_i, \hat{y}_i, \hat{z}_i, k_i)\}을 출력합니다. GT box 집합 \{b_j\}가 주어지게 되는데, feature level마다 출력되는 location을 해당 집합과 매칭함으로써 object가 존재하는 곳을 찾으려고 하는 것이죠. 저자는 dataset에 따라 하이퍼파라미터를 조정하지 않아도 되는 일반화된 function을 제공한다고 합니다. 우선 GT box b에 대해 R_k(b)는 k번째 feature level에서 b 영역 안에 포함되는 location이 몇개 있는지를 나타냅니다.

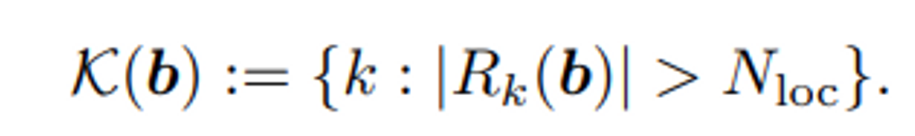
총 k개의 feature level에서 box내포함되는 location의 개수가 N_loc 이상이 된다면 해당 feature level index k를 선택하고 만약 조건에 만족하는 feature level이 하나도 존재하지 않는다면 1번째 feature level을 k(b)로 선택합니다.

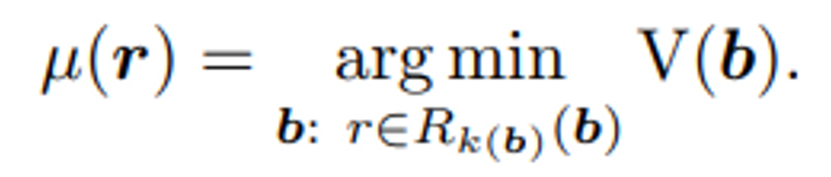
그러면 각 location에 대해 여러개의 bounding box가 할당되는데 그 중 volume이 가장 작은 box를 매칭하게 됩니다. 마지막으로 실제 GT box의 center 값 근처에 존재하는 location을 positive로 간주하는 center sampling이라는 것을 통해 location을 필터링 합니다. 즉 하나의 GT box에 대해 몇개의 location {(\hat{x}, \hat{y}, \hat{z})}이 매칭되어 해당 GT box의 label과 center 정보와도 연결될 수 있습니다.

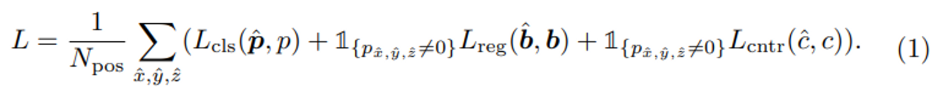
전체적인 Loss는 위의 식(1)과 같습니다. 식에서 regression loss와 centerness loss 앞에 붙어있는 식은 GT box와 매칭된 location의 수 N_pos를 의미하며 location (\hat{x}, \hat{y}, \hat{z})가 positive일 경우에만 bounding box regression loss와 centerness loss를 계산하게 됩니다. L_{cls}는 classification loss로 focal loss를 사용하며, centerness loss L_{cntr}는 binary cross entropy loss 입니다.

3.2 Bounding Box Parametrization

3D bounding box를 표현할 수 있는 방식은 axis-aligne(AABB), oriented(OBB) 두 가지가 존재합니다. AABB와 OBB의 가장 큰 차이점은 heading angle의 유무로 각 box를 표현하면 AABB는 b^(AABB) = (x, y, z, w, l, h)이고 OBB는 AABB에서 앵글 \theta가 추가되어 b^{OBB} = (x, y, z, w, l, h, \theta)로 표현할 수 있습니다. 앵글이라는 것은 물체가 회전하였을 때 박스 역시 물체가 회전한 만큼 회전하였음을 나타냅니다. 앵글 이외의 (x, y, z)는 각 박스의 중심 좌표, (w, l, h)는 박스의 width, length, height가 되겠죠. 두 개의 box parametrization에 대해 차례대로 알아보도록 하겠습니다.

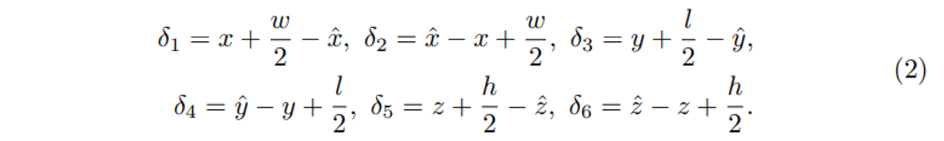
AABB parametrization

GT AABB b^{AABB} = (x, y, z, w, l, h)와 location \{(\hat{x}, \hat{y}, \hat{z})\}가 주어지면 \delta를 식(2)과 같이 계산하여 Loss 함수에서의 \hat{b}를 예측하는데 사용할 수 있습니다.

AABB의 경우 위와 같이 간단히 parameterization 할 수 있지만 heading angle이 포함되어 있는 OBB의 경우 어떻게 해야 할까요? 당시 모든 point cloud 기반 sota 방법론의 경우 heading angle 추정을 classification 이후에 regression을 통해 진행했다고 합니다. heading angle은 여러개의 bin으로 분류되어 정확한 앵글을 bin 내에서 regression을 통해 찾았습니다. indoor의 경우 bin이 0부터 2\pi 내에서 12개로 나뉘는 반면 outdoor는 road 기준 평행한지, 수직인지 2가지로 나눕니다. bin이 선택되면 heading angle은 regression을 통해 예측되는데, outdoor 기반 method는 삼각법을 통해서 이를 예측합니다. 반면 indoor에서의 object들이라고 함은 Fig3처럼 회전을 얼마만큼의 각도로 한 것인지 가늠하기 모호한 경우가 많습니다. 이런 모호한 물체에 대해서 GT angle을 annotation할 때 랜덤으로 값을 할당하게 되고 결국 angle을 분류된 bin 내에서 추정하는 것이 의미없게 될 수 있습니다. 그런 상황을 피하기 위해서 저자는 모든 가능한 heading angle 후보가 동일하다고 여기는 rorated IOU loss를 사용하여 OBB parametrization을 새롭게 제안함으로써 rotation한 각도가 모호하여 알 수 없는 경우까지 고려하고자 하였습니다.

Proposed Mobius OBB parameterization

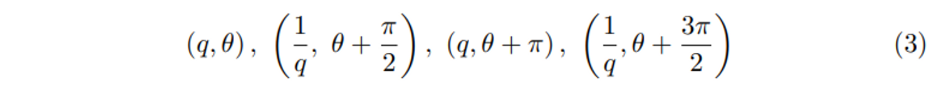
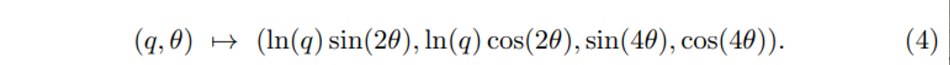
OBB parameter (x, y, z, w, l, h, \theta)를 기반으로 q = w/l 이고 x, y, z, w + l, h가 고정되어 있다고 가정하면 \theta = (0, 2\pi], q는 어떤 양수이며 (q, \theta)로 식(3)과 같이 4개의 같은 위상을 가진 bounding box를 표현할 수 있습니다. (0, 2\pi]의 원 안에서 한 바퀴를 돌며 다른 \theta 값을 가지다가 처음의 값으로 돌아와도 여전히 같은 box를 가리키기에 뫼비우스라고 칭하는 것일까요 .. 아무튼 식(3)에서 4개의 bounding box를 나타내는 식은 모두 같은 박스를 뜻하며 이를 2차원 유클리디언 공간인 Mobius strip에서 아래 사진의 과정을 거쳐 식(4)와 같이 한 점으로 나타낼 수 있다고 합니다.

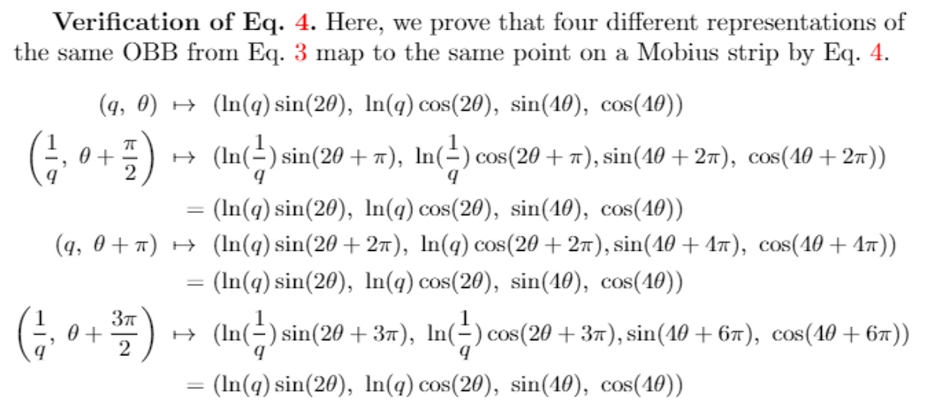
저자는 여기서 실험적으로 4개의 값으로 object box를 예측하는 것보다 앞의 두 값 ln(q)sin(2\theta), ln(q)cos(2\theta)만 사용하는 것이 더 좋은 결과를 보였기에 두 값을 가지고 식(2)에 추가적으로 식(5)까지 더해진 새로운 OBB parameterization을 정의하였습니다.

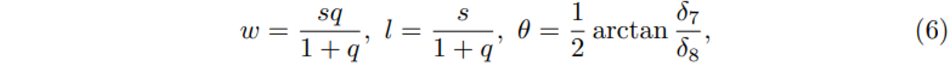
식(6)에서 q = e^{\sqrt{\delta^2_7+\delta^2_8}}이고 s = \delta_1 + \delta_2 + \delta_3 + \delta_4로, heading angle까지 고려한 OBB의 w, l 그리고 \theta를 새롭게 정의하는 것 입니다. 결국 저자가 modius OBB parameterization을 제안하면서 이야기하고 싶은 것은 indoor 환경에서 모호한 rotation angle에도 불구하고 object가 존재하는 영역을 강인하게 찾을 수 있는 방법을 제안하고자 하였습니다.

4. Experiments

4.1 Datasets

3개의 indoor dataset을 사용하여 IOU threshold 0.25와 0.5 설정에 대한 각각의 mAP로 평가하였다고 합니다. 실험 결과에 대한 시각화로 각 데이터셋의 box parameterization를 보여주기 때문에 ScanNet과 S3DIS은 AABB를, SUN RGB-D는 OBB를 계산하였음을 참고해주시면 좋을 것 같습니다.

4.2 Comparison with State-of-the-art Methods

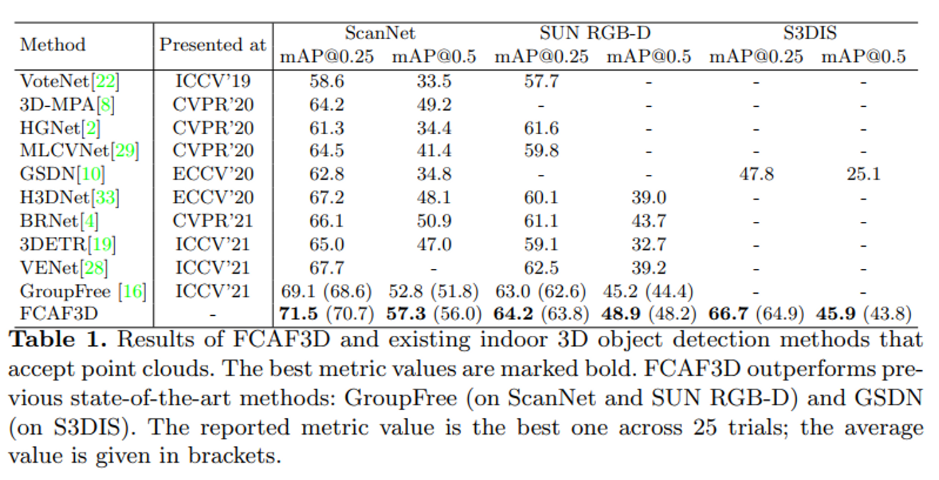
Table 1은 SOTA 방법론과 FCAF3D를 비교한 결과로 성능 표기를 5번 train하고 test하여 best 결과와 5번의 결과를 평균 낸 값으로 하였습니다. best 성능 ( 평균 성능 ) 으로 표기하였으며 이전 방법론 대비 모든 데이터셋에서 SOTA를 달성하였음을 볼 수 있습니다.

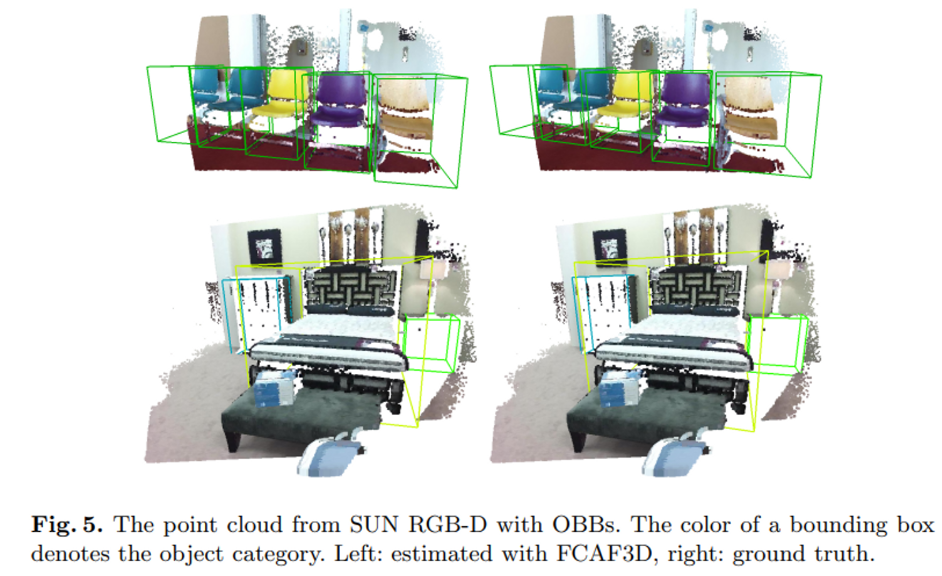
Fig 4, 5, 6은 차례대로 ScanNet, SUN RGB-D, S3DIS 데이터셋에서 AABB, OBB 추정과 GT box를 비교한 것을 시각화함으로써 미리 정해놓은 bounding box를 사용하지 않음에도 GT box와 매우 유사하게 물체를 검출할 수 있음을 강조하고 있는 것 같습니다.

Fig 4, 5, 6은 차례대로 ScanNet, SUN RGB-D, S3DIS 데이터셋에서 AABB, OBB 추정과 GT box를 비교한 것을 시각화함으로써 미리 정해놓은 bounding box를 사용하지 않음에도 GT box와 매우 유사하게 물체를 검출할 수 있음을 강조하고 있는 것 같습니다.

4.4 Comparison to GSDN

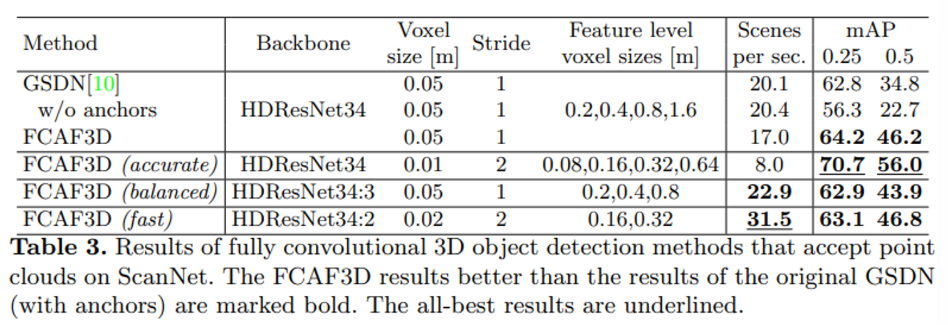
FCAF3D는 GSDN를 베이스로 방법론을 설명을 했었기에 GSDN과의 성능을 비교하는 실험도 진행하였습니다. Feature level을 동일시한 기본 모델과, best 성능이 나오도록 세팅한 모델이 accurate, 더 적은 feature level을 사용한 것이 balanced, 2개의 feature level마을 사용한 것이 fast라고 생각해주시면 됩니다. best 모델인 accurate의 경우 GSDN 대비 큰 차이를 두고 성능이 향상된 것을 확인할 수 있습니다. 또한 GSDN을 anchor free와 유사하게 하나의 anchor만을 사용하도록 세팅한 결과 mAP 0.5에서 12% 정도의 성능 하락이 있었습니다. 결과적으로 GSDN의 경우 사전에 정의해놓은 박스 setting이 없을 시 낮은 성능을 보이기에 일반화되지 않은 모델이라고 이야기하며 anchor free 방식의 FCA3D가 우수함을 강조하고 있습니다.