안녕하세요, 양희진입니다.

오늘은 6D pose estimation 문제를 풀기 위해 refinement를 어떻게 할지를 다루는 논문입니다. 수식적인 부분이 이번에도 확실히 어렵긴 한 것 같습니다. 글의 중간 중간에 제가 추가적으로 알아본 것과 제가 이해하기 위해 작성한 것을 보면서 이해하시는 데에 도움이 되셨으면 좋겠습니다.

시작하기에 앞서, 일반적으로 refinement 방법론들은 어떻게 pose 초기화를 잘 해줄지, 잘 초기화된 정보를 이용하여 미분가능한 함수를 만드는 것에 초점을 맞추는 것으로 알고 있습니다. 이러한 관점으로 글을 읽으시면 좋을 것 같습니다.

리뷰 시작하겠습니다.

Abstract

HybridPose는 hybrid intermediate representation을 사용하여 keypoint, edge vector, symmetry correspondence 등 입력 이미지의 다양한 기하학적 정보를 representation 합니다. 여기서 말하는 intermediate representation이란, 입력 데이터를 처리하고 객체에 대한 6D pose를 추정하기 위해 사용되는 데이터의 형식이나 특성을 의미하게 됩니다. 입력 데이터에 대한 정보를 압축하여 pose 추정을 좀 더 용이하게 만드는 역할을 한다고 보시면 좋을 것 같습니다. 저자는 단일 representation에 비해 hybrid representation을 사용하면 한 가지 유형의 예측 표현이 부정확할 때(예를 들면, occlusion이 되는 경우) pose regression을 통해 더 많은 다양한 특징을 활용할 수 있습니다. HybridPose에서 사용하는 다양한 intermediate representation은 모두 동일한 간단한 신경망으로 예측할 수 있으며, 예측된 intermediate representation의 outlier는 robust한 regression 모듈에 의해 필터링됩니다. 당시 SOTA였던 모델과 비교했을 때 HybridPose는 속도는 비슷하지만 정확도가 훨씬 높습니다. LM-O에서 HybridPose는 30FPS 속도로 예측하면서 ADD(-S)는 79.2%를 달성하였습니다.

1. Introduction

RGB 이미지에서 물체의 6D pose를 추정하는 것은 3D 비전의 근본적인 문제이며, 물체 인식 및 로봇과 물체 간 상호 작용에 다양하게 응용됩니다. 최근에는 딥러닝의 발전으로 해당 문제에서 상당한 진전이 있는 상황인데요. 초기 연구에서는 일반적으로 end-to-end로 pose classification/regression을 통해 공식화가 되었지만 20년 당시의 pose 추정 방법은 일반적으로 keypoint를 intermediate representation으로 활용하고 예측된 2D keypoint를 GT 3D keypoint와 align 하여 사용합니다. 이 방법은 GT pose label 외에도 keypoint를 intermediate supervision으로 통합하여 원활한 모델 학습을 하도록 유도해준다고 합니다.

Keypoint-based 방법론은 두 가지 가정이 있습니다.

1. Machine Learning 모델이 2D keypoint 위치를 정확하게 예측할 수 있다.
2. 이러한 예측은 6D pose를 regression하기에 충분한 constraint(제약 조건)을 제공한다.

하지만 위의 두 가지 가정은 실제 환경에서 다루려면 쉽게 깨지는 가정들입니다. 물체의 occlusion 및 예측을 위한 네트워크의 representation 한계로 인해 RGB 이미지만으로는 2D keypoint 좌표를 정확하게 예측하는 것이 사실상 불가능한 경우가 더 많습니다. 그래서 저자는 추가적인 representation을 제공하여 정확한 pose를 추정하도록 설계를 합니다.

입력 이미지의 기하학적 정보를 representation하기 위해 다중 intermediate representation을 활용하는 새로운 6D 포즈 추정 접근 방식인 HybridPose를 제안하게 됩니다. HybridPose는 keypoint 외에도 인접한 keypoint 사이에 edge vector를 출력하는 것을 위한 예측 네트워크를 추가합니다. 대부분의 물체가 reflection symmetry를 가지기 때문에 HybridPose는 pixel간의 symmetry 관계를 반영하는 예측된 dense pixel-wise correspondence도 활용합니다. reflection symmetry란 대상이 되는 물체에 대한 기준점을 중심으로 반대편으로 뒤집었을 때 원래의 모양과 동일한 모양이 나타나는 성질이라고 이해하시면 될 것 같습니다. 결론적으로 단일 representation에 비해 분명히 장점이 있어서 사용한 것으로 보입니다. 어떤 장점이 있는지 살펴보겠습니다.

• edge vector는 물체 부분 간의 공간 관계를 encoding하고 symmetry correspondence는 내부적인 디테일에 대해서 즉, 물체의 대칭적인 부분들 간의 일치를 찾는 것을 의미합니다. 결과적으로 HybridPose는 입력 이미지에 더 많은 정보를 통합하게 됩니다.
• HybridPose는 pose regression에 keypoint만 사용하는 것보다 더 많은 constraint을 제공하므로 예측 요소의 상당 부분이 occlusion으로 인해 outlier인 경우에도 정확한 포즈 예측이 가능합니다.
• 대칭 대응이 특히 reflection plane의 normal direction(법선 벡터)을 따라 pose 예측의 회전 구성 요소를 stable하게 합니다.

2. Related Works

Edge features

edge는 물체의 contour 등과 같은 중요한 이미지의 특징 정보를 가지고 있다고 일반적으로 알려져있습니다. 이러한 low-level 이미지 특징과 달리 HybridPose는 인접한 keypoint 사이에 정의된 semantic edge vector를 활용합니다. keypoint 간의 상관관계를 파악하고 객체의 기본 구조를 제공하는 해당 representation은 간결하고 예측하기 쉬운 장점이 있습니다. 이러한 edge vector는 pose regression을 위해 keypoint만 사용하는 것보다 더 많은 constraint을 제공하며 occlusion일 때도 강인한 장점이 있다고 합니다. 접근 방식은 edge vector의 방향과 크기를 모두 예측하고 이 벡터를 사용하여 물체의 pose를 추정합니다.

Symmetry detection from images

pose가 다른 symmetry object가 이미지에서 동일한 모양을 가질 수 있기 때문에 대칭이 포즈 추정에 모호성을 도입한다는 관점에서 대칭을 연구해 왔습니다. 여러 연구에서 symmetry transformation에도 invariant한 loss function을 설계하는 등 이러한 모호성을 해결하는 방법을 제안하고 있다고 합니다.

Robust regression

intermediate representation을 통한 pose 추정은 occlusion 및 clutter background에 의해 발생하는 예측의 outlier에 민감합니다. pose error를 완화하기 위해 2D-3D alignment 과정에서 예측된 요소에 서로 다른 가중치를 부여하는 작업도 있습니다. 반면, 저자의 접근 방식은 robust function을 추가로 활용하여 예측 요소에서 이상값을 자동으로 필터링합니다. HybridPose의 접근 방식은 robust한 목적함수의 critical point와 loss surface을 고려합니다.

3. Approach

3.1. Approach Overview

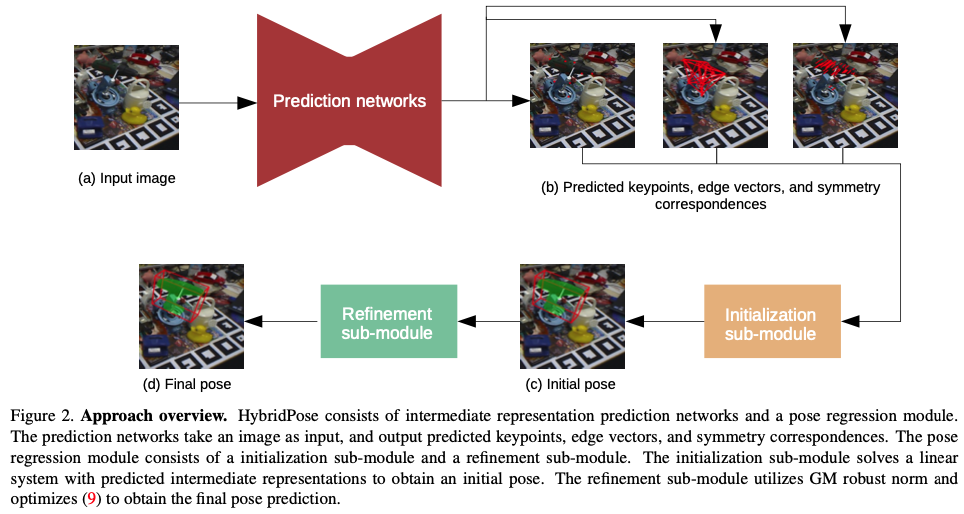
fig(2)를 보면 HybridPose는 크게 prediection module과 pose regression module로 구성되어 있는 것을 확인할 수 있습니다.

3.2. Hybrid Representation

prediction module에서 사용되는 3가지 intermediate representation에 대해 먼저 알아보겠습니다.

Keypoints

첫 번째로 사용되는 intermediate representation은 keypoint 입니다. pose estimation에 일반적으로 많이 사용되는 representation 이라고 생각하시면 좋을 것 같습니다. 입력 이미지 I가 주어지면, 미리 정의된 |\mathcal K| 키포인트 세트의 2D 좌표를 예측하기 위해 신경망 f_{\theta}^{\mathcal K}를 학습하게 됩니다. 실험에서 HybridPose는 voting 방식을 사용하여 visible keypoint와 invisible keypoint를 모두 예측할 수 있게 해주는 당시 최신 방법론이었던 PVNet을 사용했다고 합니다.

하지만 예측된 keypoint의 outlier외에도 keypoint-based 방법론의 한계는 인접한 두 keypoint간의 차이(방향 및 거리)가 객체의 pose estimation을 위해 중요한 정보를 특정 짓는 경우에 부정확한 keypoint의 예측으로 인해 pose error가 크게 발생한다는 점입니다. 즉, 특정 짓는다는 것은 물체의 pose를 결정하는 데 중요한 역할을 한다는 의미일 것이고 keypoint-based 방법론에도 detection 문제가 분명히 존재할 것입니다. 부정확한 keypoint 예측으로 인해 pose 추정 결과가가 좋지 않을 것입니다.

Edges

사전에 정의된 graph를 따라 edge vector로 구성된 두 번째 intermediate representation은 명시적으로 모든 keypoint pair 사이의 변화를 모델링 합니다. fig(2)를 보시면 HybridPose는 2D 이미지 평면에서 edge vector를 예측하기 위해 f_{\phi}^{\epsilon}(I)를 학습합니다. 이때 \varepsilon은 사전에 정의된 graph에서 edge의 수를 의미합니다. 실험에서 \varepsilon은 fully-connected graph인 |\varepsilon|=\frac{|\mathcal K|(|\mathcal K|-1)}{2}입니다.

Symmetry correspondences

마지막으로 세 번째 intermediate representation은 reflection symmetry을 반영하는 예측된 pixel-wise correspondence로 구성됩니다. 실험에서는 dense pixel-wise flow와 PVNet이 예측한 semantic mask를 FlowNet 2.0의 네트워크 아키텍처를 확장시켜 사용했다고 합니다. result symmetry correspondence는 mask 영역 내에서 예측된 pixel-wise flow을 이용하여 얻을 수 있습니다. Keypoint와 edge에 비해 대칭이 되는 correspondence가 더 많기 때문에 occlusion된 물체에 대해서도 풍부한 constraint를 제공합니다. 하지만 symmetry correspondence는 객체 pose의 회전 구성 요소에서 2개의 DoF만 제한합니다. symmetry correspondence를 다른 intermediate representation과 결합하여 사용하는 것이 필요하다고 판단을 했다고 합니다. 3D 모델에는 여러 개의 reflection symmetry plane이 있을 수 있습니다. 이러한 모델의 경우 가장 두드러진 reflection symmetry plane, 즉 원본 3D 모델에서 가장 많은 수의 symmetry correspondence를 가진 reflection symmetry plane을 기준으로 symmetry correspondence를 예측하도록 HybridPose를 학습합니다.

3.3. Pose Regression

두 번째 module은 예측된 intermediate representation들인 {\mathcal K, \mathcal E, \mathcal S}(keypoint, edge, sym corr)를 입력으로 받고 입력 이미지 I에 대한 물체의 6D pose를 출력하는 구간입니다. HybridPose는 initialization sub-module과 refinement sub-module을 결합하여 사용합니다. 두 개의 sub-module은 앞서 예측된 모든 요소들을 활용하게 됩니다. refinement sub-module은 예측된 요소들의 outlier값들에 대해 조정하기 위해 robust function을 사용하게 됩니다.

아래의 notation은 3D keypoint coordinate \bar p_{k}(1 ≤ k ≤|\mathcal K|)를 사용하고 식을 좀 더 정리하기 위해 첫 번째 module의 출력인 예측된 keypoint, edge vector, symmetry correspondences을 p_{k}, v_{e}, (q_{s, 1}, q_{s, 2})이는 2차원에 대한 정의이므로 3차원에서 정의하기 위해 homogeneous coordinate를 사용하여 각각 \hat p_{k}, \hat v_{e}, (\hat q_{s, 1}, \hat q_{s, 2})로 정의하여 사용합니다. homogeneous coordinate는 camera intrinsic matrix에 의해 정규화가 된다고 합니다.

Initialization sub-module

첫 번째 sub-module인 initialization sub-module을 살펴보겠습니다. 해당 sub-module은 (R_I, t_I)와 예측 요소 사이에서 constraint를 활용하고 affine space에서 (R_I, t_I)를 풀고 alternating optimzation 방식으로 SE(3) 공간으로 projection 합니다. 이를 위해 예측 요소의 각 유형에 대해 다음과 같은 difference vector에 대해 알아보겠습니다.

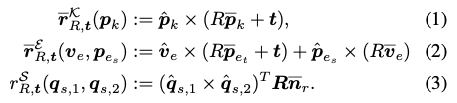
먼저 e_{s}, e_{t}는 edge e의 end vertex이고, \bar v_e = \bar p_{e_{t}} - \bar p_{e_{s}}, \bar n_{r}은 canonical system에서 reflection symmetry plane의 법선(normal)입니다. HybridPose는 EPnP를 수정하여 initial pose를 생성하게 되는데요. 예측 요소에서 eq(1)~(3)의 제약 조건을 결합하여 Ax=0의 homogeneous linear system을 사용하게 되는데, 선형대수적 관점에서 생각해보면 x는 항상 해를 가지게 됩니다. 이때 x는 두 가지의 해를 가질 수 있는데, 자명 해(x=0), 자명하지 않은 해(자명한 해를 제외한 모든 해의 집합, 즉 무수히 많은 해를 의미)를 가질 수 있습니다. 해가 무조건 존재하는 것을 이용하여 문제를 풀어가는 것으로 이해를 하였습니다. 여기서 A는 matrix이고 해당 차원은 (3|\mathcal K|+3|\mathcal E|+|\mathcal S|)\times 12이고 이러한 문제를 해결하기 위해 x=[r_{1}^T, r_{2}^T, r_{3}^T]{12 \times 1}^T은 affine 공간에서 회전 및 이동에 대한 파라미터가 포함된 벡터가 되게 됩니다. keypoint, edge vector, symmetry correspondence간의 상대적 중요도를 eq(2), eq(3)을 하이퍼파라미터로 사용하기 위해 저자는 \alpha{E}, \alpha_{S}로 다시 나타내고 matrix A를 재조정합니다.

EPnP에서는 x를 eq(4)와 같이 계산하게 됩니다. 여기서 v_i는 A의 i 번째로 smallest right singular vector를 의미합니다. 가장 이상적인 케이스는 예측 요소에 아무런 노이즈가 없는 경우이므로 N=1인 경우를 의미하게 되고 해당 경우에는 x=v_1이 최적의 솔루션이 되게 됩니다.

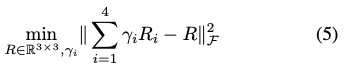
노이즈가 많은 경우 해당 알고리즘은 잘 동작하지 않게 되고 해당 EPnP에서 사용한 최적의 파라미터인 N=4를 사용하여 최적의 x를 찾기 위해 eq(5)와 같은 목적 함수를 사용하여 alternating optimization 과정을 통해 latent variable \gamma_i와 rotation matrix R을 최적화합니다. 이때 R_i는 \gamma_i의 처음 9개의 원소로부터 재생성되고, 최적의 \gamma_i를 구한 후, \Sigma_{i=1}^{4}\gamma_{i}R_{i}를 rigid transformation으로 projection합니다.

Refinement sub-module

두 번째 sub-module인 refinement sub-module에 대해 알아보겠습니다. eq(5)는 hybrid intermediate representation을 결합하고 좋은 initialization은 제공하는 것은 많은 방법론에서도 적용하는 것을 보아 입증된 것으로 보입니다. 하지만 여기서 outlier에 대해서는 해결을 못 하는 점, 그리고 eq(1), (2)에서 keypoint-based pose 추정에서 효과적인 것으로 알려진 projection error를 더 최소화하지 못 하는 점이 있다고 합니다.

초기의 물체에 대한 pose(R^{init}, t^{init})의 이점을 잘 활용하기 위해 refinement sub-module은 local optimization을 수행하여 물체의 pose를 refine합니다.

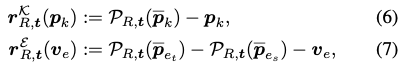
저자가 제안한 2개의 projection error와 관련된 difference vector를 eq(6), (7)를 설명하겠습니다. 여기서 \mathcal P_{R, t}(\mathbb R^3→ \mathbb R^2)는 현재 pose에서의 projection operator를 의미합니다. eq(6)을 살펴보면 앞서 2차원에 대한 keypoint와 projection된 3차원의 keypoint는 차원이 같기 때문에 연산이 가능한 것으로 보이고, eq(7)은 각 edge vertex의 끝점에 대해 projection을 수행하고 difference를 수행하는 것으로 보입니다.

저자는 예측된 outlier를 제거하기 위해 RANSAC이 아닌 GM(German-McClure) function을 사용하였다고합니다.

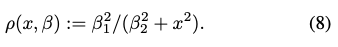
eq(8)의 \rho는 GM function에 대한 정의라고 생각하시면 될 것 같습니다. 입력으로 하이퍼파라미터 \beta에 따른 최적의 x를 찾는 function으로 이해하였습니다. 해당 함수에 대해서 찾아보니 중간값과 중위 편차를 사용하여 이상치에 덜 민감하게 반응하도록 한다고 합니다.

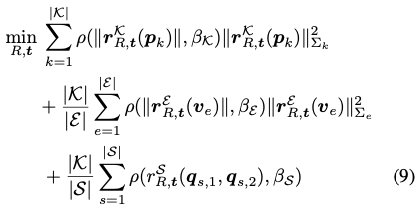
eq(9)는 HybridPose의 pose refinement를 위해 non-linear 문제를 해결하는 식입니다. 이때 하이퍼파라미터인 \beta_{\mathcal K}, \beta_{\mathcal E}, \beta_{\mathcal S}는 keypoint, edge vector, symmetry correspondence를 의미합니다. \Sigma_{k}, \Sigma_{e} 는 keypoint, edge vector의 예측에 부여된 covariance 정보를 의미합니다. ||의 연산은 예를 들어 ||x||{A} = (x^TAx)^{\frac {1}{2}}를 나타낸다고 이해하시면 될 거 같습니다. 예측의 covariance를 사용할 수 없는 경우, \Sigma{k}=\Sigma_{e}=I_2(단위행렬로 보입니다.)로 간단하게 설정한다고 합니다. eq(9)의 optimization 문제는 R^{init}, t^{init}부터 시작하여 Gauss-Newton method를 사용하여 해결한다고 합니다. Gauss-Newton method는 미적분학에서 사용했던 함수가 미분이 가능할 때 사용 가능한 approximation method 입니다.

3.4. HybridPose Training

Initialization sub-module

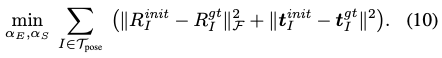
Initialization sub-module의 출력은 R^{init}, t^{init}이 됩니다. 해당 정보를 이용하여 eq(10)의 optimization 문제를 푼다면 최적의 하이퍼파라미터 \alpha_{E}와 \alpha_{S}를 구할 수 있습니다. 하이퍼파라미터의 수가 다소 적고 pose initialization 과정에서 명시적인 식이 딱히 없으므로 현재의 해에 대한 하이퍼파라미터 값들에 대해 gradient를 맞추는 방식으로 gradient를 계산한다고 합니다. 그런 다음 최적화를 위해 Backtracking Line Search를 수행한다고 합니다. gradient descent은 함수의 기울기를 이용하여 반복적으로 최솟값을 향해 찾아가는 단계적인 알고리즘입니다. Backtracking Line Search는 최적화 알고리즘을 수행하는 단계 중 step size를 결정하는 데에 사용되는 과정이므로 최적화 알고리즘을 수행하는 내부적인 과정입니다.

Refinement sub-module

\beta = \{\beta_{\mathcal K}, \beta_{\mathcal E}, \beta_{\mathcal S}\}를 해당 sub-module의 파라미터로 설정을 합니다. critical point과 critical point 주변의 loss function에 의해 최적의 솔루션이 결정되는 즉 딥러닝을 통한 알고리즘을 활용하기 때문에 파라미터를 추정하는 것에 대해 특정한 조건을 만족할 필요가 없으므로 unconstraint 최적화를 통해 문제를 해결하게 됩니다.

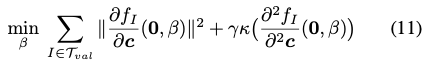
eq(11)을 보면 저자는 2가지의 목적 함수를 정의합니다. 첫 번째로는 \frac {\partial f_{I}}{\partial c}(0, \beta) \approx0입니다. 즉, GT가 대력 임계점일 것이라고 정의합니다. 두 번째로 \kappa를 최소화하는 것입니다. 이때 \kappa(\frac{\partial^2 f_{I}}{\partial^2c}(0, \beta))= \lambda_{\max}(\frac{\partial^2 f_{I}}{\partial^2c}(0, \beta))/\lambda_{\min}(\frac{\partial^2 f_{I}}{\partial^2c}(0, \beta))를 의미하게 됩니다. 이러한 세팅으로 \beta를 최적화를 수행합니다. 이때 c는 현재의 추정 pose와 GT pose의 차이를 SE(3)에서 encoding하는 것을 의미합니다. \gamma=10^{-4}로 설정하였다고 합니다.

4. Experimental Evaluation

4.1. Experimental Setup

Datasets

실험은 LM, LM-O에서 진행하였고 |\mathcal K|=8개의 keypoint를 선택했다고 합니다. edge vector는 각 keypoint-pair를 연결하는 vector로 정의됩니다. 각 객체의 에지의 총 개수는 |\mathcal E|=\frac{|\mathcal K|(|\mathcal K|-1)}{2}로 28개 입니다.

4.2. Analysis of Results

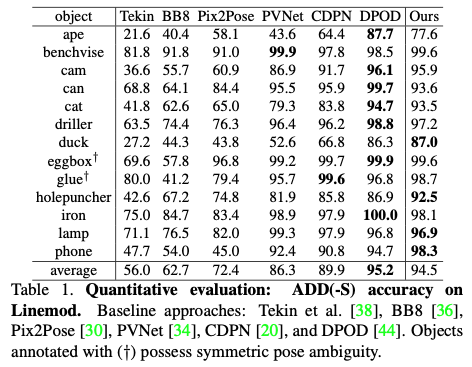
Baseline comparison on Linemod

HybridPose는 keypoint를 예측하는 데 사용하는 backbone 모델인 PVNet 보다 Table(1)을 통해 성능이 더 좋은 것을 확인할 수 있습니다. 하나의 객체에 대한 클래스를 제외한 나머지 모든 객체에 일관되는 성능 향상을 보여주는 것을 보아 hybrid representation를 사용했을 때의 이점을 증명한 것으로 저자는 분석을 하였습니다. HybridPose는 DPOD와 비교했을 때 6개의 객체 클래스에 대해 성능 향상을 한 것을 확인할 수 있고, DPOD의 장점은 데이터 augmentation과 입력 이미지와 projection된 이미지 간의 dense correspondence에 대한 명시적 모델링에서 비롯되며, 둘 다 물체의 occlusion이 없는 상황에 적합합니다.

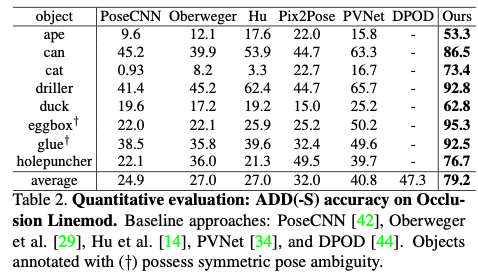
Baseline comparison on Occlusion Linemod

마찬가지로 PVNet 보다 성능이 더 우세한 것을 확인할 수 있습니다. 또한 HybridPose는 해당 데이터셋에서 그 당시 최신 모델이었던 DPOD보다 67.4% 더 뛰어난 성능을 보였습니다. 추가적으로 data augmentation 및 correspondence 계산에서 occlusion에 대한 모델링이 어렵기 때문에 DPOD와 같은 렌더링 기반 접근 방식이 occlusion 객체에 대해서 잘 작동하지 않아 average가 낮은 것으로 보입니다. DPOD 논문 내용 중 실험에도 LM-O에 대한 실험 내용은 없기 때문에 따로 표기를 하지 않은 것으로 보이네요.

4.3 Ablation Study

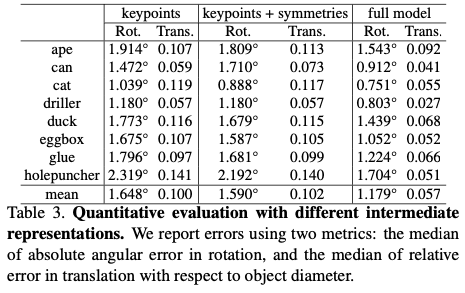
keypoint 정보만 이용, keypoint+sym corr정보 이용 full model(keypoint + edge vector + sym corr)이용에 따른 성능 결과 표입니다. 경우의 수가 좀 더 많았을텐데 3가지만 다룬 정량적 평가라서 아쉬운 것 같습니다.

5. Conclusion

이 논문에서는 keypoint, edge vector, symmetric correspondence를 활용하는 6D pose estimation의 접근 방식인 HybridPose를 봤습니다. 실험 결과 표는 따로 없지만 30 FPS로 실시간 예측이 가능하면서 정확도 면에서도 당시 SOTA를 달성했던 모델입니다. HybridPose는 occlusion이나 극단적인 pose(pose error가 큰 경우)에도 강인하게 작동하도록 설계를 하여 좋은 성능을 달성한 것으로 이해하였습니다.