[WACV 2021] TCA: Temporal Context Aggregation for Video Retrieval with Contrastive Learning

안녕하세요. 백지오입니다.

아홉 번째 X-REVIEW는 Video Retrieval 분야에서 2021년 제안된 논문인 TCA입니다.

아시다시피 영상은 수많은 프레임(이미지)들로 구성되며, 이러한 프레임들에 포함된 시각적 정보들이 시간이 흐름에 따라 변화하는 temporal한 속성을 갖고 있습니다. 이러한 시간에 따른 맥락 정보, temporal context는 영상에 있어 매우 중요한 정보이지만, 이러한 정보는 영상에서 시간적으로 멀리 떨어진 영역에 걸쳐 분포해 있기 때문에, 고정된 kernel 크기를 갖는 CNN과 같은 방법으로는 잡아내기 어렵습니다.

TCA는 feature의 long-range dependency를 잘 잡아내는 transformer의 self-attention을 이용해 이러한 temporal context를 잡아냅니다. 이를 통해 feature-level 방법, video-level 방법 모두에서 video retrieval의 성능을 높일 수 있었습니다.

또한, 논문의 저자들은 일반적으로 Triplet Loss 기반의 metric learning을 이용하는 기존의 video retrieval 방법들과 달리 Softmax 기반의 손실 함수인 InfoNCE Loss를 사용한 Contrastive Learning으로 모델을 학습합니다. 이때 gradient 분석을 통하여 Contrastive Learning이 자동적으로 hard example mining을 수행하는 것과 같은 효과를 내어, 매 배치마다 직접 negative sample을 뽑아 triplet을 구성하는 triplet loss보다 효과적임을 증명합니다.

정리하면, 본 논문의 contribution은 다음과 같습니다.

1. Transformer를 이용하여 frame들 간의 long-range dependency를 포함한 temporal context를 aggregation한 feature 생성
2. Contrastive Learning이 Triplet Loss 대비 효율적임을 그래디언트 분석을 통해 확인

그럼, 리뷰 시작해보겠습니다.

---

Method

먼저, 데이터셋을 core와 distractor로 나눈다. Core에는 두 영상이 유사한지(near-duplicate, complementary scene 등)의 label을 가지고 있는 영상들이 포함되어 있으며, distractor는 대량의 negative sample에 해당하는 영상들이 포함되어 있다.

RGB 영상 $\mathbb{x}_r \in \mathbb{R}^{m\times n\times f}$은 먼저 frame-level descriptor sequence $\mathbb{x}_f \in \mathbb{R}^{d\times f}$나 video-level descriptor $\mathbb{x}_v \in \mathbb{R}^d$로 인코딩된다. 두 descriptor $\mathbb{x}_1, \mathbb{x}_2$의 유사도는 $sim(, \mathbb{x}_1, \mathbb{x}_2)$와 같이 나타낸다.

우리의 목표는 영상 $\mathbb{x}_1, \mathbb{x}_2$가 연관된 경우 $sim(f(\mathbb{x}_1), f(\mathbb{x}_2))$를 최대화하고, 반대의 경우 최소화하는 임베딩 함수 $f(\cdot)$을 만드는 것이다. 여기서 $f(\cdot)$은 temporal context aggregation modeling module로, frame-level descriptors $\mathbb{x} \in \mathbb{R}^{d\times f}$를 입력받아 video-level descriptor $f(x)\in \mathbb{R}^d$ 혹은 정제된 frame-level descriptor $f(x)\in \mathbb{R}^{d\times f}$를 반환한다. ($d$는 feature 길이, $f$는 frame의 수)

Feature Extraction

저자들은 각 프레임을 사전학습된 CNN 모델에 입력하여 $\text{L}_3\text{-iRMAC}$을 추출하였다.
CNN 모델의 각 합성곱 계층에서 생성된 feature map을 $3\times 3$ 크기로 풀링하여 $\mathcal{M}^k \in \mathbb{R}^{3\times 3\times c^k}$의 크기로 만든다. ($c^k$는 $k$번째 합성곱 계층의 출력 채널 수) 그다음, feature map을 채널 축을 남기고 더하여 $\mathcal{M}^k\in \mathbb{R}^{c^k}$로 만들고, $l_2$ normalization을 수행한다.

얻어진 $\text{L}_3\text{-iRMAC}$ feature를 1차원으로 연결하고, PCA를 적용하여 차원 축소를 진행한다. 마지막으로 $l_2$ normalization을 적용하여 frame-level descriptor $\mathbb{x}\in \mathbb{R}^{d\times f}$를 얻는다.

Temporal Context Aggregation (TCA)

저자들은 Transformer 구조를 활용해 Temporal Context Aggregation을 수행했다.

파라미터 행렬 $W^Q, W^K, W^V$를 통해 video descriptor $\mathbb{x} \in \mathbb{R}^{d\times f}$를 쿼리 $Q$, 키 $K$, 벨류 $V$로 선형 변환하고, 아래 식을 통해 셀프 어텐션을 수행했다.

$$\text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{d}})V.$$

그다음, LayerNorm을 수행하고 Feed Forward 계층을 거쳐 최종적으로 트랜스포머 인코더의 출력 $f_\text{transformer}(\mathbb{x}) \in \mathbb{R}^{d\times f}$를 얻었다. 이때, 멀티 헤드 어텐션 구조도 사용했다고 한다.

이를 통해 특성의 크기는 변화하지 않으나, 마치 NLP에서의 트랜스포머가 각 단어들의 연관성을 분석하는 것처럼 각 프레임들의 연관 관계가 어텐션에 의해 특성에 반영된다.

이렇게 얻은 특성에서 단순히 시간축에 대한 평균을 구하면 video-level descriptor $\hat{f}(\mathbb{x}) \in \mathbb{R}^d$를 얻을 수 있다. (frame-level descriptor를 그대로 사용해도 된다.)

Contrastive Learning

어떤 앵커(기준) 영상과 양성(관계있는) 영상, 그리고 음성 영상들의 video-level representation을 $\mathbb{w}_a, \mathbb{w}_p \mathbb{w}_n^j(j = 1, 2, \cdots, N-1)$로 나타낼 때, 이들의 유사도 점수는 아래와 같다.

$$ s_p = \frac{\mathbb{w}_a^T\mathbb{w}_p}{||\mathbb{w}_a|| ||\mathbb{w}_p||}$$

$$ s_n^j = \frac{\mathbb{w}_a^T\mathbb{w}_n^j}{||\mathbb{w}_a||||\mathbb{w}_n^j||}$$

이때, InfoNCE Loss를 다음과 같이 나타낼 수 있다. ($\tau$는 temperature 하이퍼 파라미터)

$$\mathcal{L}_{nce} = -\log\frac{\exp(s_p / \tau)}{\exp(s_p) + \sum^{N-1}_{j=1} \exp(s_n^j / \tau)}$$

로그함수는 1에서 0으로 최소화되고 0에 가까워질수록 커지므로, 음성 영상과 앵커 영상의 유사도가 낮아질수록 Loss가 낮아지게 된다. 저자들은 이에 더불어, 메모리 뱅크의 개념을 적용하였다.

각 배치를 구성할 때, 코어 데이터셋에서 한 쌍의 양성 쌍을 구성하고, distractor에서 $n$개의 음성 영상을 가져와 배치를 구성한다. 이들은 인코더를 거쳐 video-level descriptor로 변환되고, 이때 모든 배치의 음성 샘플들은 concatenate되어 메모리 뱅크를 구성한다.

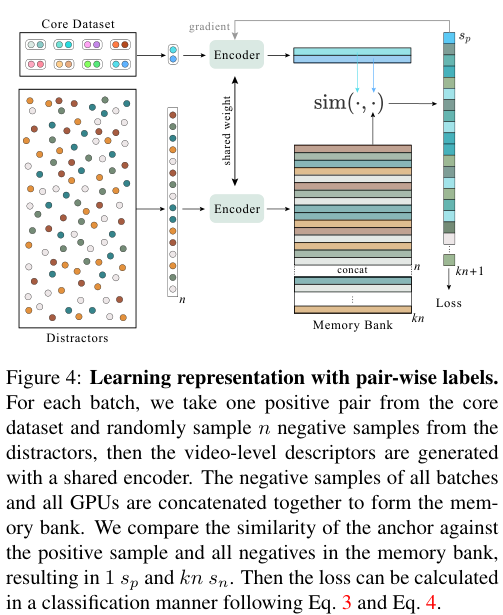
앵커 영상에 대해, 양성 영상 하나와 메모리 뱅크의 모든 영상과의 유사도를 구하여 한 개의 $s_p$와 $kn$개의 $s_n$을 얻게 되며, 이렇게 얻어진 $s$들에 대해 앞선 Loss 함수가 적용된다. 저자들은 InfoNCE 다음으로 소개된 Circle Loss도 소개한다.

$$\mathcal{L}_{circle} = -\log \frac{\exp (\gamma \alpha_p(s_p – \triangle_p)}{\exp(\gamma \alpha_p (s_p – \triangle_p)) + \sum^{N-1}_{j=1} \exp(\gamma \alpha_n^j (s_n^j – \triangle_n))}$$

$\gamma$는 scale factor로 InfoNCE의 $\tau$와 유사하다. $m$은 relaxation margin으로, $\alpha_p = [1+m-s_p]_+, a_n^j = [s_n^j + m]_+, \triangle_p = 1-m, \triangle_n = m$을 정의한다. InfoNCE Loss에 비하여 Circle Loss는 $s_p, s_n$에 별도의 adaptive penalty를 적용하고 클래스 내(within-class), 클래스 간(between-class) margin을 적용하여 최적화한다.

One Step Further on the Gradients

앞선 Supervised Contrastive Learning 연구에서 batch contrastive loss가 feature normalization과 함께 자동적으로 hard positive와 negative sample에 집중한다는 것을 그래디언트 분석을 통해 알아내었다고 한다. 저자들은 추가적인 분석을 통해 이러한 효과가 contrastive loss 뿐 아니라 Softmax 계열 손실함수와 feature normalization를 함께 사용하면 공통적으로 얻을 수 있는 효과임을 밝혀냈다. InfoNCE Loss의 원형이라 할 수 있는 Softmax 함수는 다음과 같다.

$$ \mathcal{L}_{softmax} = -\log \frac{\exp(s_p)}{\exp(s_p) + \sum^{n-1}_{j=1}\exp(s^j_n)}$$ 

Softmax Loss에서 easy negative는 그래디언트에 작은 영향을 주는 반면, hard negative는 큰 영향을 주게 된다. Normalized video-level representation $\mathbb{z}* = \mathbb{w}* / ||\mathbb{w}*||$에 대하여 Softmax 함수의 $\mathbb{w}_a$에 대한 그래디언트는 다음과 같다.

$ \sigma(\mathbb{s})_p = \exp(s_p) / [\exp(s_p) + \sum^{N-1}_{j=1} \exp(s^j_n)]$이고, $ \sigma(\mathbb{s})_n^j = \exp(s_n^j) / [\exp(s_p) + \sum^{N-1}_{j=1} \exp(s^j_n)]$일 때, easy negative는 앵커와의 유사도가 -1에 수렴($\mathbb{z}_a^T\mathbb{z}_n^j \approx -1$)한다. 그러므로 $\sigma(\mathbb{s})^j_n|| (\mathbb{z}_n^j – (\mathbb{z}_a^T\mathbb{z}^j_n)\mathbb{z}_a || = \sigma(\mathbb{s})^j_n \sqrt{1-(\mathbb{z}_a^T\mathbb{z}^j_n)^2} \approx 0.$가 성립한다.

한편, hard negative에 대해서는 $\mathbb{z}_a^T\mathbb{z}^j_n \approx 0$이므로, $\sigma(\mathbb{s})_n^j$가 일반적인 값을 갖는다. 때문에 위 식이 0 이상의 값을 갖고, 결과적으로 그래디언트에 큰 영향을 주게 된다. 이전 연구들은 feature normalization이 feature들을 작은 값으로 나누어 hard sample들이 상대적으로 큰 그래디언트를 갖게 함을 직관적으로 보였다. 한편 저자들은 이를 처음으로 그래디언트 분석을 통해 증명해 내었다고 한다.

저자들은 이를 바탕으로 video retrieval 분야에서 많은 컴퓨팅을 요구하는 hard negative mining을 포함한 triplet loss를 사용하는 것보다, 자동으로 hard negative에 집중하는 효과를 갖는 softmax 기반 손실 함수를 사용하는 contrastive learning을 수행하고, memory bank 기법을 사용해 negative sample의 크기를 키우는 것이 학습 효율에 좋다고 주장한다.

Similarity Measure

학습 단계에서의 연산 효율을 높이기 위해, 모델은 $l_2$-normalized video-level descriptor $f(x) \in \mathbb{R}^d)$간의 비교를 수행한다. 이는 행렬의 닷 연산을 통해 쉽게 수행할 수 있다.

한편, frame-level descriptor $f(\mathbb{x}) \in \mathbb{R}^{d\times f}$를 사용할 때도, Chamfer Similarity 연산을 통해 쉽게 영상의 유사도를 구할 수 있다. $\mathbb{x} = [x_0, x_1, \cdots , x_{n-1}], \mathbb{y} = [y_0, y_1, \cdots , y_{m-1}]$에 대하여 $x_i, y_j \in \mathbb{R}^d$일 때, chamfer similarity 연산은 다음과 같이 정의된다.

$$ sim_f(\mathbb{x}, \mathbb{y}) = \frac{1}{n}\sum^{n-1}_{i=0} \max_j x_iy_j ^T$$

$$ sim_{sym}(\mathbb{x}, \mathbb{y}) = (sim_f(\mathbb{x}, \mathbb{y}) + sim_f(\mathbb{y}, \mathbb{x}))/2$$

이 연산에 대한 자세한 설명은 필자의 ViSiL 리뷰를 참고해 주기 바란다.

Experiments

저자들은 TCA를 Near-Duplicate Video Retrieval (NDVR), Fine-grained Incident Video Retrieval (FIVR), Event Video Retreival (EVR)에 대하여 실험하였다. 먼저 학습에는 VCDB 데이터셋을 사용하였는데, 이때 VCDB에 포함된 전체 10만 개의 distractor 중 99181개를 다운로드할 수 있었다고 한다.

평가에는 각각 CC_WEB_VIDEO (NDVR), FIVR-200K (FIVR), EVVE (EVR)를 사용하였으며, FIVR 데이터셋은 다음과 같은 세 가지 하위 라벨을 갖는다.

• Duplicate Scene Video Retrieval (DSVR)
• Complementary Scene Video Retrieval (CSVR)
• Incident Scene Video Retrieval (ISVR)

Implementation Details

특성 추출은 초당 1개의 프레임을 추출하여 진행되었으며, 앞서 설명한 방식대로 진행되었다. intermediate feature는 ResNet-50의 4개 블록에서 추출되었으며, PCA는 VCDB에서 랜덤 하게 추출한 997090개의 frame-level descriptor에서 학습되어 iMAC과 $L_3$-iRMAC에 적용되었다. 이를 통해 whitening과 3840에서 1024로의 차원 축소가 진행되었고, 마지막으로 $l_2$ normalization을 적용했다.

트랜스포머 모델은 8개의 어텐션 해드와 0.5의 dropout_rate, 2048차원의 feed-forward 계층으로 구성되었다.

학습 과정에서 모든 영상은 64 frame으로 padding 되거나 랜덤 하게 crop 되었고, 평가에서는 영상의 원래 길이를 사용하였다. 모델 최적화는 $10^{-5}$의 learning rate를 갖는 Adam으로 진행하였고, cosine annealing learning rate 스케쥴러를 적용하였다. 배치 사이즈 64로 40 에포크 학습하였고, 각 배치마다 distractor에서 $16\times 64$개의 negative sample을 뽑아 memory bank에 넣었다. memory bank의 크기는 4096으로 하였다.

Ablation Study

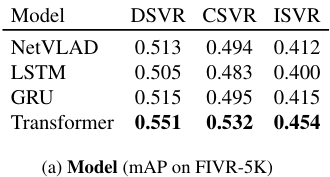
저자들은 먼저 temporal context aggregation에 사용하는 모델에 따른 성능 차이를 비교하였다. 동일한 VCDB 데이터셋에서 iMAC feature를 기반으로 실험하였을 때, NetVLAD, LSTM, GRU와 같은 방법 대비 Transformer를 사용하여 temporal context aggregation을 수행하는 것이 성능의 향상을 보였다. 저자들은 이것이 self-attention을 통해 long-term dependency를 잡을 수 있어 그렇다고 한다.

다음은 특성 추출에 사용하는 Feature와 학습에 사용된 Loss Function의 비교이다. iMAC보다는 $L_3$-iRMAC을 사용하는 것이 성능이 좋았으며, 손실 함수는 Circle Loss가 약간 더 좋았다고 한다.

메모리 뱅크의 크기는 일반적으로 커질수록 좋았으며, 메모리 뱅크를 사용하지 않는 triplet 방법과 비교를 수행하였을 때 메모리 뱅크의 사용이 성능도 높고, 학습 시간도 적게 소요되었다.

또한 저자들은 MoCo와 비슷한 방식으로 Momentum을 적용하여 negative sample들을 보관한 큐를 서서히 업데이트하는 방식을 실험해 보았는데, 오히려 이를 적용하지 않는 것이 성능이 좋았다. 저자들은 MoCo 방식이 메모리 뱅크가 작을 때는 적절한 타협책이 될 수 있으나, 뱅크가 크다면 오히려 좋지 않은 것으로 보았다.

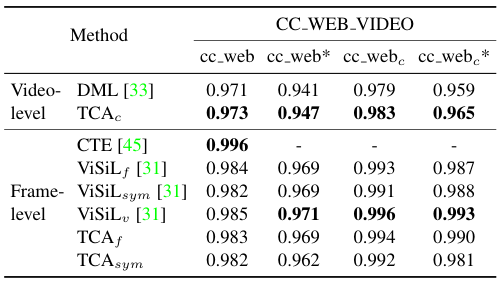
마지막으로 descriptor의 유사도 계산 방식을 비교하였다. 일반적인 코사인 유사도와 chamfer 유사도, 대칭 chamfer 유사도, chamfer 유사도와 비교용 신경망의 방법을 비교하였는데, chamfer 유사도가 가장 좋았다. 이후 실험 결과에서, $\text{TCA}$는 $\text{L}_3\text{-iRMAC}$과 Circle Loss를 사용한 모델이며, $\text{TCA}_c$는 코사인 유사도, $\text{TCA}_f$는 chamfer 유사도, $\text{TCA}_{sym}$은 대칭 chamfer 유사도, $\text{TCA}_v$는 비교용 신경망을 사용한 결과이다.

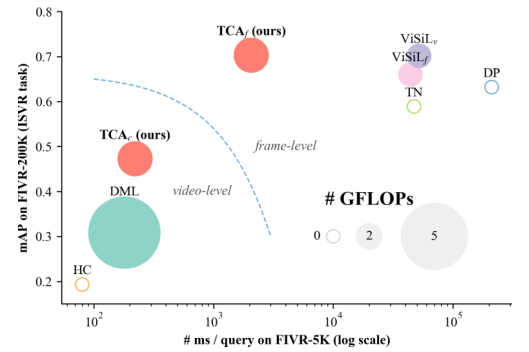
Comparison Against SOTA

저자들은 기존 SOTA 모델들과 TCA의 비교를 수행하였다. Frame-level feature를 사용하는 모델 중에는 $\text{ViSiL}_v$가 가장 성능이 높으나, TCA의 목표는 간단하고 효율적인 유사도 계산과 좋은 video representation을 생성하는 것이었기에, 유사도 계산 신경망을 별도로 만들어 사용하는 $\text{ViSiL}_v$보다 TCA와 동일한 chamfer 유사도 연산을 사용하는 $\text{ViSiL}_f$를 비교하는 것이 적절하다고 주장한다. 이렇게 생각하면 TCA가 좋은 video representation을 만드는 것은 어느 정도 일리가 있다고 생각이 되는데, 결국 성능 자체는 따라잡지 못한 것이 좀 아쉽다.

FIVR와 EVR task에서, video-level 기반의 $\text{TCA}_c$가 기존 모델들에 비해 확실한 성능 향상을 보였다. frame-level feature 기반 방법론에서도 TCA가 꽤 좋은 성능을 보여주지만, 여전히 ViSiL에는 약간 못 미치는 모습이다.

다만, 좋은 video representation을 만든다는 목표만큼은 확실히 달성하였음을 보여주는 실험으로 보인다.

한편 표에는 나타나지 않았지만, TCA는 $\text{ViSiL}_v$ 대비 약 22배 빠른 추론 속도를 보인다고 한다. 또한, TCA가 FIVR task 중 ISVR에서는 ViSiL을 앞선 것을 확인할 수 있는데, 이를 통해 저자들은 TCA가 semantic 정보를 추출하는데 강점이 있을 수 있다고 주장하였다.

한편 EVR task에서 video-level 기반의 TCA가 일부 frame-level 기반 방법들을 앞서는 성능을 보여주는데, 이 역시 ISVR과 비슷한 맥락으로, 어쩌면 EVR task에서는 temporal 정보나 fine-grained spatial 정보가 그리 중요하지 않을 수도 있다고 한다.

Qualitative Results

저자들은 마지막으로 랜덤으로 추출한 FIVR-5K subset에 t-SNE를 적용한 결과를 보인다. DML 방버 대비 유사한 영상들이 더 가까이, 구분되게 뭉쳐있는 것을 확인할 수 있다. 

저자들은 attention weight를 시각화해 본 위 이미지를 통해, TCA가 영상에서 멀리 떨어진 영역들에서도 중요한 부분을 잘 찾아내어 semantic dependency를 잘 모델링하여, 더 중요한 정보를 잘 담은 video representation을 만든다고 주장하였다.

---

Video Retrieval이 흔히 feature extraction, similarity calculation의 과정으로 구성되어 이 부분들에서만 문제를 생각해 봤었는데, transformer를 통해 temporal context aggregation이라는 과정을 추가해주어 feature를 강화하는 것이 제게 나름 새롭게 느껴진 논문이었습니다.

한편, TCA 외에도, Contrastive Learning의 효율성에 대한 분석이 생각 외로 비중있게 다루어졌는데요.

이 부분도 저는 별 생각없이 triplet loss를 받아들이고 있었던 것 같아, 여러모로 연구자라면 이런 저런 것들을 다 의심해봐야 하는구나 싶은 생각이 들었습니다.

한편, 읽으면서 생소한 개념이 조금 등장하였는데 (메모리 뱅크 등), 이런 부분들은 더 보충해야겠다는 생각이 들면서도, transformer는 제가 이전에 빡세게 공부한 덕에 이해가 금방 되어서, 공부의 보람이 느껴지는 논문이었습니다!

리뷰는 여기서 마치겠습니다.

요즘 날씨가 너무 더운데, 다들 건강하시길 바랍니다.

감사합니다!