[CVPR 2023] Improving Weakly Supervised Temporal Action Localization by Bridging Train-Test Gap in Pseudo Labels

안녕하세요. 이번 X-Review는 23년도 CVPR에 게재된 논문 <Improving Weakly Supervised Temporal Action Localization by Bridging Train-Test Gap in Pseudo Labels>입니다.

바로 리뷰 시작하겠습니다.

1. Introduction

Weakly-Supervised Temporal Action Localization(WTAL) task는 비디오 snippet 단위의 label, 즉 찾아야 하는 action의 temporal annotation을 학습 때 사용하지 않기 때문에 근본적 문제에 시달립니다. 학습 중엔 video-level label만 사용하기 때문에 결국 아래 그림과 같이 어떠한 비디오가 주어진 GT 클래스로 분류되는 데에 있어 가장 구별력을 갖는 snippet들만 action이라고 분류되는 것입니다.

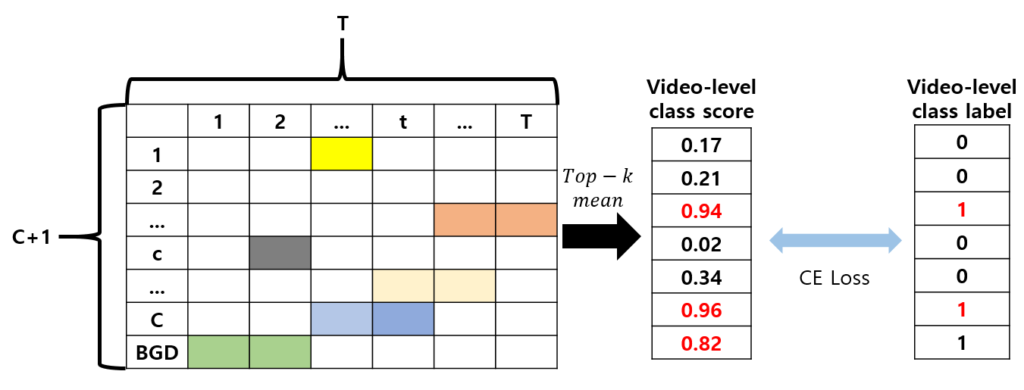
분류에 높은 영향을 미치는 snippet들만 action으로 분류된다는 것은 두 가지 관점에서 부정확한 예측 결과를 초래할 수 있습니다. 분류 학습으로부터 localization을 수행하다 보면 실제로는 action인 구간 처음과 끝의 애매한 영역들이 포함되지 않는 incompleteness 상황을 만들어낼 수도 있고, 아니면 action은 아니지만 클래스와 꽤 관계 있는 snippet에 대해 over-confident한 예측값을 만들어낼 수도 있는 것입니다. 이러한 상황을 “Localization by Classification” 문제라고 칭하고, 이를 완화하고자 대략 22년도 방법론들부터는 직접적인 localization 학습을 위한 snippet-level pseudo label을 학습 중에 만들어 내 사용하기도 했습니다.

하지만 근본적으로 temporal annotation을 가지고 있지 않기 때문에 실제 action 경계를 보고 pseudo label을 생성할 수는 없을 것입니다. 결국은 classification 학습 관점에서 얻은 snippet-level pseudo label에서 출발하여 이에 여러 장치를 추가하며 denoising 함으로써 실제 GT temporal annotation과 최대한 유사한 pseudo label을 만들어내고 높은 성능을 기대할 수 밖에 없는 상황인 것이겠죠.

이러한 WTAL 연구 상황 속에서 본 논문도 정제된 pseudo label 생성 방법론을 제안하고, 제목에서 알 수 있듯 pseudo label 생성 및 정제 과정에서 WTAL의 학습 시와 inference 시 파이프라인 차이로부터 발생하는 비일관성을 메꾸는 방향으로 여러 모듈을 제안하게 됩니다.

지금 Introduction에서는 저자가 제안하는 방법론들의 용어적인 측면에서만 살펴보고, 자세한 내용은 아래에서 알아보겠습니다.

---

우선 pseudo label을 만들어 localization 학습에 사용하는 기존 방법론들에 대해 잠시 알아보겠습니다.

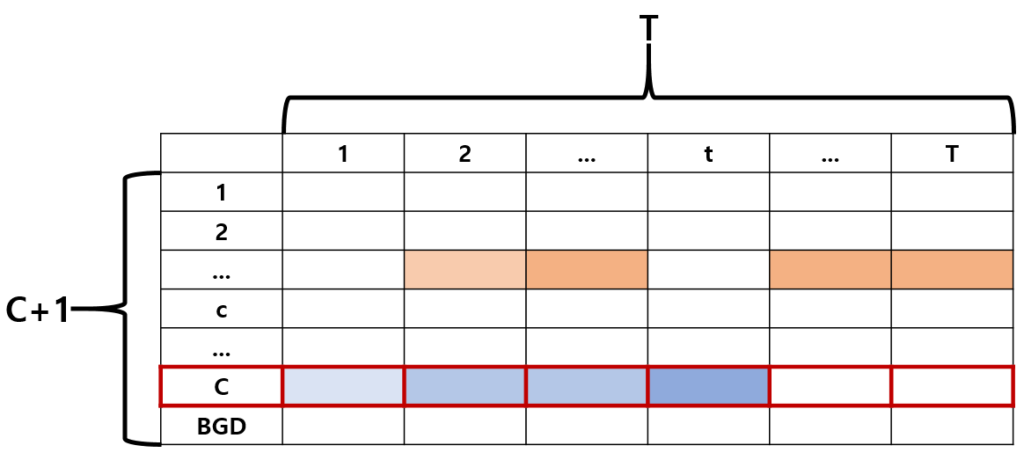
특정 비디오에서 하나의 클래스에 대한 pseudo label을 얻는 가장 쉬운 방법은 위와 같이 video feature에 1D Conv 여러 개를 태워 얻은 Temporal Class Activation Map (TCAM)일 것입니다. C번째 클래스에 대한 pseudo label은 위 그림에서 붉은 테두리가 쳐진 부분입니다. 하지만 T-CAM은 첫 번째 그림에서도 보여드렸듯 video-level label로 학습되기 때문에 앞서 이야기한 “Localization by Classification” 문제를 벗어날 수가 없겠죠.

그럼 위와 같이 T-CAM으로부터 pseudo label을 생성하는 방식 말고 또 다른 방법으로는, 학습 중인 모델이 만들어내는 proposal을 pseudo label로 사용하는 것입니다. 원래 WTAL task의 결과물이 action 구간을 만들어내는 것이니, 학습 중인 모델이 만들어내는 proposal을 다음 학습 단계에서의 pseudo temporal annotation으로 사용하는 것입니다. 이러한 방식이 궁극적으로 temporal annotation을 볼 수 없는 Weakly-supervised 상황에서는 사실 상 최선이라고 볼 수도 있겠죠.

그럼 학습 중인 모델의 proposal은 어떠한 방식으로 얻게 될까요?

학습을 마친 모델로부터 최종적인 proposal을 만들어 낼 때에는 입력된 비디오에 대해 기본적인 CAS를 추출한 후 actionness score 등을 반영해 action에 더욱 특화된 CAS를 만들어내고, 이로부터 여러 threshold를 적용해 redundant한 proposal들을 만들어내고 NMS를 거쳐 최종 proposal을 얻게 됩니다.

이를 좀 더 자세히 설명하자면 위 그림의 “C”번째 클래스 score인 붉은 테두리 쳐진 부분을 시작으로, 별도 모듈에서 구해준 actionness score를 snippet-wise로 곱하여 action snippet이 좀 더 두드러지는 score를 가질 수 있도록 먼저 연산해줍니다. 그럼 결국 1~T 번째 snippet 각각이 C번째 클래스에 속할 확률 score를 얻을 수 있게 되는데, T개의 snippet score에 대해 0.1부터 0.925까지 0.025 간격으로 multiple threshold를 적용해 snippet score가 threshold 이상인 proposal candidate group을 redundant하게 만들어냅니다. 이후에는 이렇게 생성된 proposal candidate 하나하나의 Outer-Inner Contrast score(OIC)를 해당 proposal의 score로 지정하고 NMS를 적용해 최종 proposal을 만들어내는 것입니다.

참고로 Outer-Inner Contrast score는 만들어진 proposal 내부의 snippet score와 proposal 외부의 앞뒤 일부 구간의 snippet score를 빼서 얻는 것으로, 좋은 proposal이라면 현재 proposal 구간 내에서만 충분히 높은 score를 가지며 외부 앞뒤 일부 구간의 score는 확연히 낮게 나오며 Outer-Inner Contrast score가 높게 나올 것입니다. 이 점수를 각 proposal에 대한 confidence score로 사용하는 것입니다. 위와 같은 과정을 모든 클래스에 대해 반복해주면 하나의 비디오에 대한 최종 proposal을 얻을 수 있게 되겠죠.

위 과정을 거쳐 proposal을 만들 수 있을 것입니다. 이로부터 pseudo label을 얻는 과정은 또 다를텐데요, model -> proposal -> pseudo label 생성 과정에서 저자는 2가지 문제점을 지적합니다. 본 논문은 저자가 지적하는 2가지 문제점을 개선하여 얻은 pseudo label로 효과적인 localization 학습을 수행해 성능을 올려보자는 컨셉인 것입니다.

우선 본 논문의 contribution을 통해 어떠한 모듈들이 사용되는지 정리하고, 이어 저자가 지적한 문제점과 모듈에 대해 자세히 알아보겠습니다.

Contribution

• We propose a Gaussian Weighted Instance Fusion Module, which can effectively generate high-quality action boundaries
• We propose a novel LinPro Pseudo Label Generation strategy by transforming the process of pseudo-label generation into a l1-minimization problem
• We propose to utilize \Delta pseudo labels to enable model with self-correction ability for the generated pseudo labels
• SOTA

대략적으로 위 모듈 각각은 pseudo label 생성을 위한 양질의 proposal 생성 / pseudo label 생성 / pseudo label의 효과적 활용 이라는 컨셉을 가지고 있다는 점을 알 수 있습니다.

2. Method

Overview

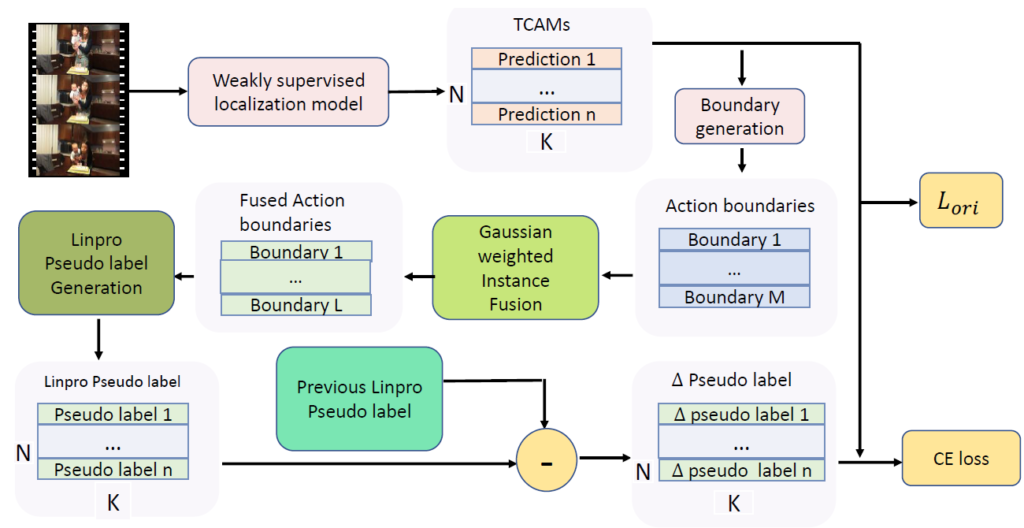
그림 1을 통해 방법론의 Overview를 확인할 수 있습니다. Introduction에서 제가 설명한 방식대로 파란 박스인 “Action boundaries”를 만들어내고, Gaussian Weighted Instance Fusion 모듈을 통해 무언가 개선된 “Fused Action boundaries”를 얻습니다. 이후 개선된 proposal을 바탕으로 localization 학습에 사용할 pseudo label을 만들어내는 “LinPro Pseudo label Generation” 과정을 거쳐 pseudo label을 얻고 \Delta pseudo labels 방식을 사용해 효과적인 학습을 이루어내고 있습니다. 각 모듈이 왜 제안되었는지, 저자가 어떤 문제점을 제기한 것인지, 어떤 역할을 하는지 알아보겠습니다.

2.1 Gaussian Weighted Instance Fusion

저자가 지적하는 첫 번째 문제점은 NMS입니다. 모델이 다양한 정보를 취합해 만든 proposal candidate에 NMS를 거쳐 이상적으로는 하나의 실제 action instance에 대해 나머지를 다 지우고 하나의 proposal만 살리게 됩니다. 하지만 proposal들은 temporal annotation 없이 만들어 낸 값이기 때문에, 저자는 NMS를 적용했을 때 사라져버리는 proposal들에도 충분히 유의미한 정보들이 존재할 것이라고 생각합니다.

이렇게 버려지는 proposal들의 정보도 함께 사용하기 위해 Gaussian Weighted Instance Fusion 모듈이 등장합니다. 겹치는 proposal들을 한 gaussian 분포의 샘플들로 가정하고, OIC score를 해당 분포에서 샘플링될 확률로 두어 평균 score로 추정함으로써 겹치는 proposal들이 gaussian 분포로 fusion된 하나의 proposal로 재탄생할 수 있도록 해주는 것입니다. 이렇게 fusion된 proposal로부터 pseudo label을 만든다면 temporal annotation이 없는 상황에서 조금 더 많은 정보를 활용하며 합리적인 양질의 action 경계를 학습할 수 있을 것이라고 주장하고 있습니다.

Introduction에서 설명드린 proposal 생성 과정 중 multiple threshold를 적용해 특정 클래스 c에 대해 총 M개의 proposal이 생성(NMS 이전)되었다고 생각해보겠습니다. A=\{a_{1}, \cdots{}, a_{M}\}는 proposal들의 집합이고 하나의 proposal a_{i} = (c_{i}, q_{i}, s_{i}, e_{i})로 표현되며 각각은 예측된 클래스, OIC score(confidence score), 시작 지점, 끝 지점을 의미합니다.

이후 아래 수식 1과 같이 가장 confidence score가 높은 proposal a_{*}과의 tIoU가 threshold h_{fuse}보다 높은 proposal들의 집합 \mathcal{I}_{*}를 얻을 수 있습니다.

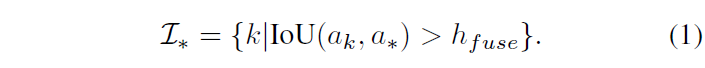
그러면 \mathcal{I}_{*}에는 confidence score가 가장 높은 proposal a_{*}과 겹치는 proposal들이 모여있을 것입니다. 기존의 NMS를 적용하면 a_{*} 이외의 모든 proposal은 삭제되지만, 저자는 이들의 정보를 살리기 위해 \mathcal{I}_{*} 내 proposal들의 \blacktriangle{} \in{} \{q, s, e\} 확률 분포가 아래 수식 (2)와 같이 gaussian 분포를 이룰 것으로 가정합니다.

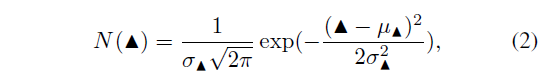
그럼 이제 각 분포의 \blacktriangle{} 평균을 실제 proposal 샘플의 \blacktriangle{} 평균으로 match 시켜주어야 할 것입니다. \mathcal{I}_{*} 내 proposal들을 하나의 분포로 합칠 때, 각 proposal이 아무래도 동등한 영향력을 행사하는 것은 부적절하겠죠. 그래서 저자는 각 proposal의 confidence score를 normalize 하여 합쳐진 proposal의 \blacktriangle{} \in{} \{q, s, e\}를 구해줍니다.

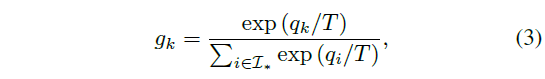
현재 proposal의 score인 OIC score q_{k}는 다른 proposal과의 관계를 고려한 점수가 아니므로 수식 (3)과 같이 softmax를 통해 집합 내 proposal들의 정규화된 weight g_{k}를 구해주게 됩니다. T는 temperature hyperparameter입니다. 이렇게 얻은 g_{i}의 분포가 수식 (2)와 유사해지도록 CE loss를 최소화합니다.

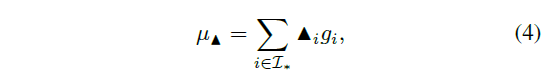
이렇게 얻은 proposal 별 gaussian weight를 적용하여 수식 (4)와 같이 fused proposal의 \mu{}_{\blacktriangle{}}를 구해줍니다. 수식 (4)에서의 \mu{}_{q}, \mu{}_{s}, \mu{}_{e}가 \mathcal{I}_{*} 내 모든 proposal들을 가우시안 가중치로 합쳐 만든 proposal의 confidence score, 시작 지점, 끝 지점이 되는 것입니다.

이후 전체 proposal set A=\{a_{1}, \cdots{}, a_{M}\}에서 \mathcal{I}_{*} 내 proposal들을 제거하고, 위 과정을 A가 빌 때까지 반복하게 됩니다.

2.2 LinPro Pseudo Label Generation

저자가 지적하는 두 번째 문제는, snippet 단위의 pseudo label을 만들어주어야 하는 상황에서 예측된 proposal들이 겹쳐있는 경우가 있어 겹치는 snippet의 pseudo label score를 어떻게 지정해주어야 할지 애매하다는 점입니다. 앞서 Gaussian Weighted Instance Fusion 모듈을 통해 fused proposal까진 만들었다고 해도, 이를 snippet-level의 pseudo label로 변환하기 위해서는 한 snippet이 둘 이상의 proposal에 포함되어 있는 경우 해당 snippet의 pseudo label score는 어떻게 지정해줄 것인지 정해주어야 합니다.

만약 Guassian Weighted Instance Fusion 모듈을 통해 얻은 proposal들에 대해 단순 thresholding을 거쳐 0 / 1의 hard label을 pseudo label로 사용하게 되면 0~1 사이로 정교하게 예측된 confidence score의 정보를 모두 잃을 뿐만 아니라 겹치는 2개의 proposal에 대해 action 경계를 학습하지 못하고 2개의 proposal을 하나로 인식해 잘못된 정보를 학습하게 될 것입니다.

Proposal 및 snippet 단위의 confidence score와 action 경계를 잘 활용하기 위해 저자는 LinPro Pseudo Label Generation 모듈을 제안합니다. LinPro는 linear programming으로, Gaussian Weighted Instance Fusion 모듈을 통해 얻은 proposal로부터 최적의 snippet-level pseudo label을 생성하는 문제를 l1-minimization 문제로 전환하여 해결하게 됩니다. 이 때 두 가지 constraint를 줍니다.

현재 저희는 각 snippet을 엮어 만든 proposal에 대한 score를 가지고 있는 상황입니다. 이 때 첫 번째 constraint는 생성된 pseudo label의 평균이 각 proposal의 confidence score \mu{}_{q}와 유사해지도록 하는 것입니다. 이와 같은 constraint를 통해 추후 pseudo label 생성 시 각 snippet이 속하는 proposal의 confidence score를 무시하지 않는 양질의 pseudo label score를 만들어낼 수 있을 것입니다.

두 번째 constraint는, 생성된 pseudo label 값들이 모두 uniform 해야 한다는 것입니다. 하나의 action instance에 대해 생성되는 pseudo label은 uniform한 분포를 가지도록 constraint를 주는것인데, action instance 내 포함되는 snippet들은 결국 전부 동일한 action class이면서 하나의 action 구간이기 때문에 action 구간 범위 내에서는 pseudo label 값이 uniform한 분포를 갖도록 제한을 두는 것으로 보입니다.

먼저 첫 번째 constraint를 다루기 위해 각 proposal instance를 linear constraint로 변환합니다. 특정 클래스 c에 대해 n개의 proposal을 얻었다면, l차원짜리 벡터 n개를 선언합니다. l은 snippet 개수이고, 정리하자면 아래 수식과 같습니다.

• \{W_{j} \in{} \mathbb{R}^{l}|j = 1 \ldots{} n\}

위 값이 랜덤으로 초기화되는 것은 아니고, proposal의 inner, outer, background 영역에 따라 1, -1, 0으로 할당됩니다.

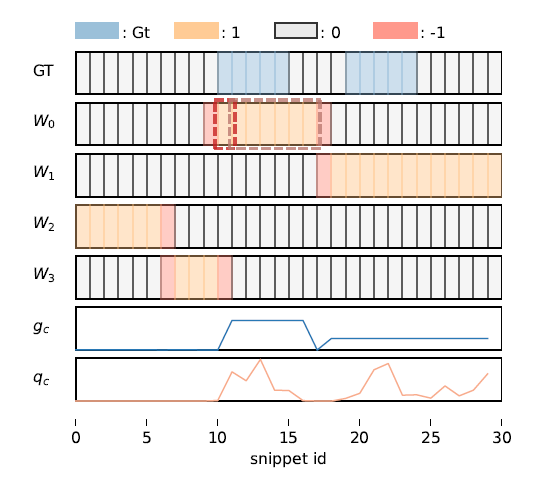
그림 2에서 각 proposal마다 1로 할당된 영역이 기존 proposal 내부 영역이고, proposal 길이에 따라 앞뒤로 outer 영역을 정의해 -1을 붙여줍니다. Inner도 outer도 아닌 영역은 background로 0이 할당됩니다.

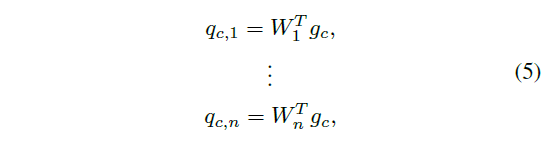
수식 (5)에서 g_{c}는 클래스 c에 대해 생성된 한 비디오에서의 pseudo label이고, 저희가 얻어야 하는 대상입니다. q_{c, i}는 c번째 클래스의 i번째 proposal에 대한 confidence score입니다. 앞서 gaussian fusion 단계에서 얻은 proposal의 score일 것입니다.

아래 수식 (6)을 통해 linear programming의 목적과 조건을 알 수 있습니다. 목적이 pseudo label의 l1-norm 최소화인데, 이는 중요하지 않은 snippet의 pseudo label 값을 빠르게 0으로 수렴시키고 중요한, 즉 proposal 별 W 합이 커 inner 영역에 많이 존재하는 snippet의 중요도를 극대화하기 위함입니다.

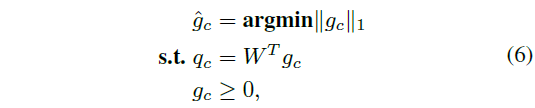
이와 같은 최적화 과정을 통해 proposal의 confidence score를 고려하는 pseudo label \hat{g}_{c}를 얻을 수 있지만, 두 번째 constraint인 uniform-shaped pseudo label은 보장되지 않습니다. 이를 보장해주기 위해 먼저 inner-outer-background 중 동일한 영역에 포함되는 snippet들을 “equivalent snippets”로 정의하고, “equivalent snipppet”들의 평균 \hat{g}_{c} 점수를 구해 그 평균으로 \hat{g}_{c}의 pseudo label 값을 대체하게 됩니다.

전체 K개의 클래스에 대해 반복적으로 위 과정을 수행해 pseudo label을 얻고 concat하여 최종 pseudo label G \in{} \mathbb{R}^{l \times{} k}를 만들어냅니다.

2.3 \Delta Pseudo Label

방법론의 마지막 파트인 \Delta Pseudo Label은 별도의 모듈이라기보단 학습 때 적용하는 방식이라고 생각하시면 됩니다. 실제 코드를 보면 총 350에포크 중 200에포크까지는 pseudo label 생성 없이 기본적인 CAS로만 학습을 하는데요, 200에포크 이후부터는 앞선 모듈을 적용해 만든 pseudo label과 CAS L을 CE Loss로 학습하며 아래 수식과 같이 j번째 snippet을 예로 학습할 수 있게 됩니다.

• \mathcal{L}_{ce} = \Sigma{} CE(\text{softmax}(L_{j}),G_{j})

위와 같이 학습하는 경우 클래스 c에 대한 j번째 snippet 학습의 negative gradient는 아래 수식 (7)과 같습니다.

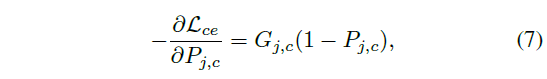
수식 (7)에서 P_{j} = \text{softmax}(L_{j})이고 여기서 P_{j, c}는 0 ~ 1 사이, 즉 (1-P_{j, c})는 항상 양수이며 수식 (6)에 따라 pseudo label 값 G_{j, c}도 양수값을 가지게 됩니다.

이에 따라 CAS의 값을 추출하는 parameter가 항상 양의 방향으로만 갱신되므로 최적의 학습을 수행한다고 볼 수 없을 것입니다. 또한 아무리 200에포크 이후에 pseudo label을 생성한다고 해도 부정확하거나 변동이 심할 수도 있겠죠.

저자는 이러한 문제를 완화하기 위해 200에포크 이후에, 생성한 pseudo label로부터 직접 학습하는 것이 아니라 이번에 생성한 pseudo label 이전 에포크 t-1에서 생성한 pseudo label의 차이인 \Delta Pseudo Label 값을 목표로 두고 학습을 수행하며, 수식으로는 아래와 같습니다.

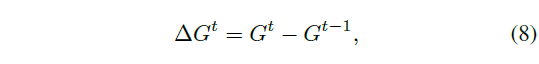
이렇게 생성한 \Delta Pseudo Label \Delta{}G^{t}를 목표로 CAS를 학습하면 snippet의 negative gradient는 아래 수식 (9)와 같습니다.

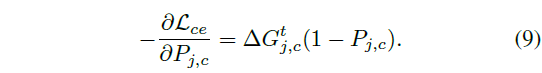
수식 (9)에서는 \Delta{}G^{t}가 양수와 음수 모두 가능하기 때문에 학습도 마찬가지로 양방향으로 가능해지는데, 설명에 따라 gradient 관점에선 유리해보이지만 실제 delta 값이 P_{j, c}보다 작고 0에 가까운 +라면 다음 step에서의 CAS 값은 되려 작아지는 방향으로 학습하는 것으로 이해하고 있었어서 왜 잘 동작하는지 쉽게 납득이 가지 않지만, 이는 실제 값들의 scale과 CAS의 원소값 형태를 살펴보아야 할 것 같습니다. 코드가 일부만 공개되어 아직 확인해볼 수는 없는 상황입니다.

해당 학습 방식과 관련되어 제 이해를 위해 첨언 주신다면 감사드리겠습니다.

2.4 Details

본 방법론의 학습 및 inference 세부 사항을 짚어보고 실험 파트로 넘어가겠습니다.

앞서 말씀드렸듯 본 방법론의 모듈에 따른 pseudo label 생성은 총 350에포크 중 200에포크 이후에 수행됩니다. 코드를 보니 22년도 CVPR에 게재된 RSKP 방법론을 베이스로 두고 있네요. 200에포크 이후엔 15~25에포크마다 pseudo label을 갱신하며 학습하게 됩니다. 매 에포크마다 \Delta{}G^{t}가 변하지는 않겠네요.

Inference 시에는 기존 방법론들과 유사하지만 큰 차이점으로 NMS를 수행하지 않습니다. Introduction에서 설명드린 proposal 만드는 방법 중 multiple threshold까진 동일하게 수행하되, 이후 NMS가 아닌 저자의 Gaussian Weighted Fusion 모듈의 방식을 따라 최종 proposal을 만들어낸다고 합니다.

3. Experiments

3.1 Datasets

학계에서 벤치마킹하는 데이터셋은 아래 표와 같습니다.

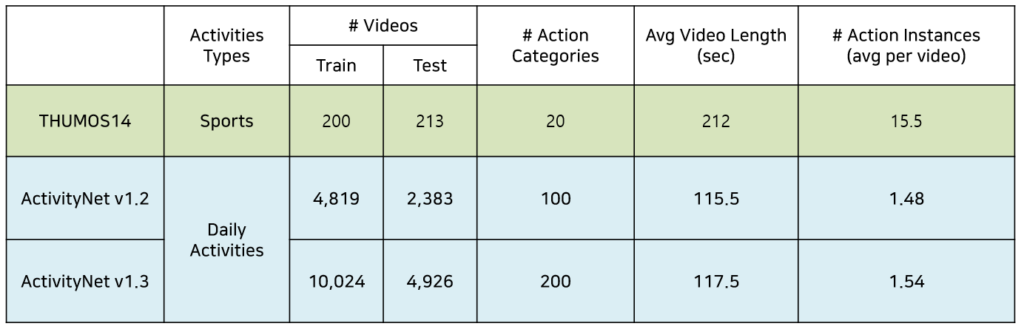
THUMOS14 데이터셋은 모든 방법론들이 벤치마킹하고, ActivityNet 데이터셋의 경우 최근 방법론들은 v1.3 위주로 벤치마킹을 수행하고 있습니다. 본 논문도 그에 맞게 THUMOS14와 ActivityNet v1.3 데이터셋에 대한 성능을 리포팅하고 있습니다. 보통 Ablation 실험은 데이터 개수가 상대적으로 적은 THUMOS14 데이터셋을 대상으로 수행됩니다.

3.2 Comparison with State-of-the-art Methods

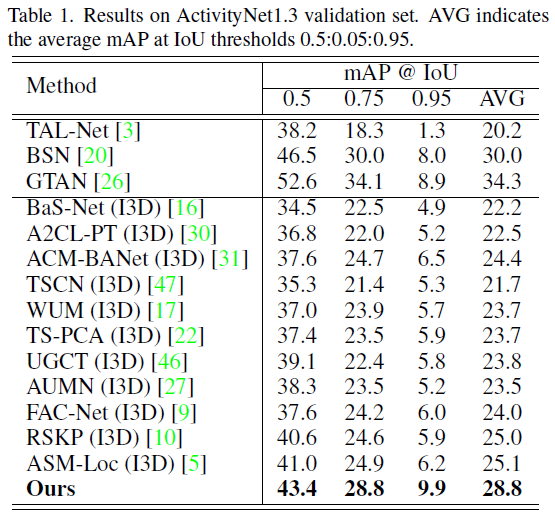
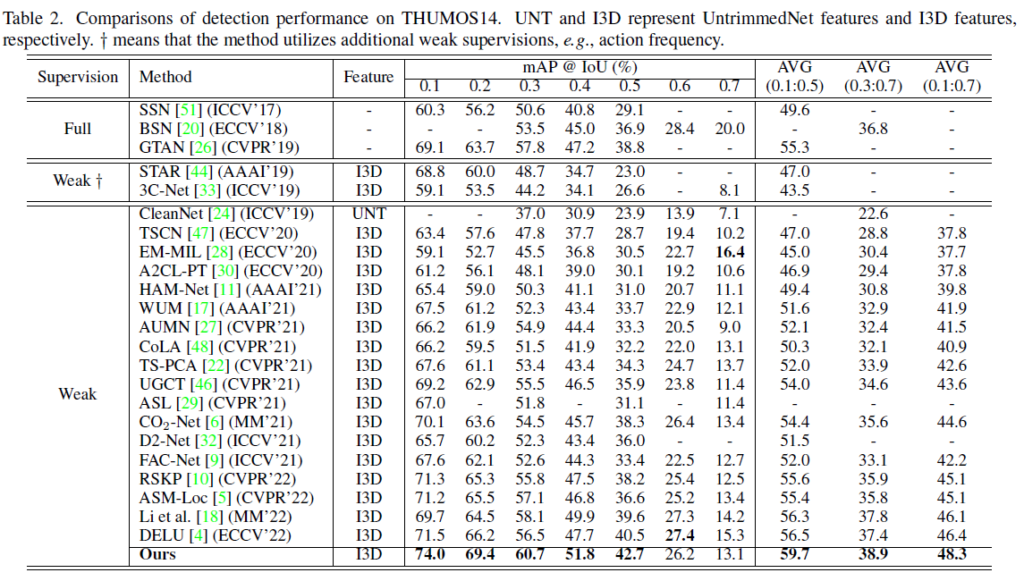
표 1, 2는 각각 ActivityNet v1.3과 THUMOS14 데이터셋에서의 벤치마크 성능입니다.

올해 게재된 논문들 기준으로 성능이 가장 높은 방법론은 아니지만 두 데이터셋에서 모두 작년 방법론들 대비 많이 오른 성능을 보여주고 있습니다. 다만 ActivityNet v1.3에서 0.95의 tIoU 기준으로 9.9%라는 굉장히 높은 성능을 보여주고 있는 것이 pseudo label이 기존 방법론보다 정교하게 만들어졌다는 것을 알 수 있었습니다.

ActivityNet 데이터셋이 비디오 개수는 많지만 길이도 조금 더 짧고 한 비디오에 포함되는 action 개수가 적은 편인데요, 그런 상황속에서는 높은 tIoU 기준으로도 좋은 성능을 보이지만 한 비디오에 포함되는 action 개수가 훨씬 많은 THUMOS14 데이터셋에서는 0.7의 tIoU에서 23년도 방법론들은 물론 22년도 방법론들보다도 낮은 성능을 보이는 것을 보니 뭔가 다발적으로 action이 발생하는 경우 action과 action 사이 짧은 background에는 pseudo label이 제대로 대응하지 못하고 있나봅니다.

저자가 벤치마크 결과에 대해 별다른 분석을 보여주고 있진 않습니다.

3.3 Ablation Study

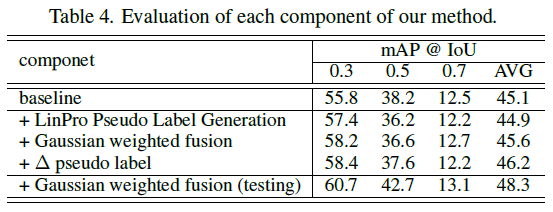
표 4는 모듈 별 ablation 성능입니다.

앞서 말씀드렸듯 베이스라인 성능은 22년도 RSKP 방법론이고 표 4에서 가장 눈에 띄는 점은 단연 Inference 시 NMS를 Gaussian fusion 모듈로 대체했을 때의 성능 향상폭입니다. 이를 통해 저자의 주장인 NMS에 의해 버려지는 정보가 너무 많다는 것이 입증되었다고 볼 수 있을 것입니다.

또한 방법론적으로는 어떠한 효과를 불러올지 잘 예측이 안가던 \Delta{} pseudo label 학습 방식도 평균 성능을 많이 올려준 것을 볼 수 있습니다.

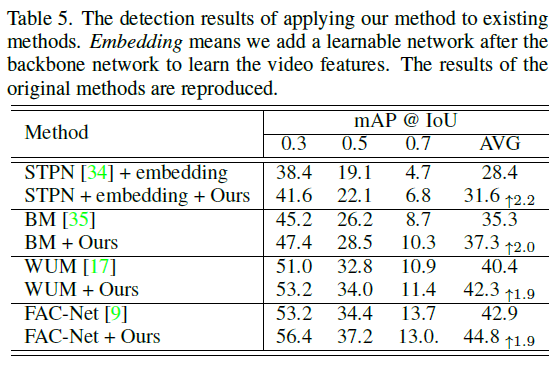
표 5는 저자의 모듈을 이전 방법론들에 추가하는 경우 성능 향상폭을 보여주고 있습니다. RSKP에 적용했을 때 만큼은 아니지만 일관적으로 많은 방법론들에서 성능이 많이 오르는 것을 알 수 있었습니다.

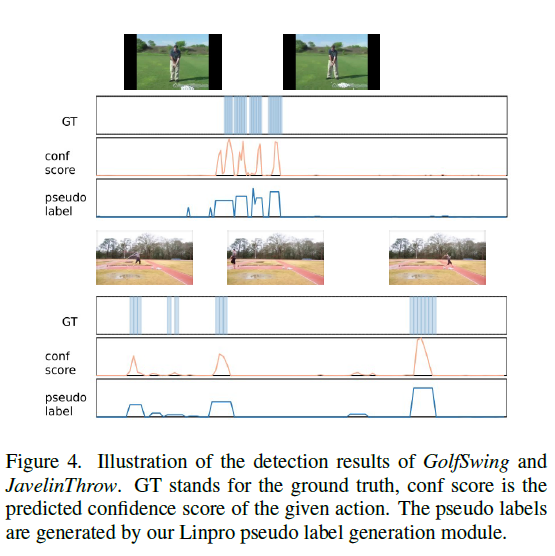
그림 4는 정성적 결과입니다. Conf score는 snippet 단위의 score인데 확실히 discriminative한 snippet을 기준으로 주변으로 갈수록 점수가 많이 떨어지는 것을 볼 수 있습니다.

애초에 베이스 방법론에서 conf score가 높게 나오지 않으면 아무리 GT라도 잡아내지 못하는 것은 어쩔 수 없고, 저자의 의도대로 conf score를 잘 보존하며 uniform한 분포를 가지는 pseudo label을 만들어내는 것을 볼 수 있습니다.

Conclusion

기존에 계속 연구되던 pseudo label 기반 방법론들의 연장선과 같은 논문이었습니다. 중간에 막혔던 부분이나 시원하게 해결되지 않은 내용이 곳곳 있었는데, 코드가 정식으로 공개되면 살펴보아야겠습니다. 본 논문에서 소개된 모듈 하나하나의 호흡이 길고 치밀하게 설계되어 있어 저자가 오랜 고심끝에 낸 연구 결과라는 생각이 듭니다.

22년도 방법론은 철저하게 inference framework는 고정한 채로 앞쪽 학습 부분에서 어떠한 아이디어를 붙일지의 싸움이었는데, 23년도 방법론으로 넘어오며 관습처럼 쓰이던 학습 방식과 inference framework에서의 변화도 많이 발생하는 것 같습니다.

이상으로 리뷰 마치겠습니다.