[ECCV 2016] Identity Mappings in Deep Residual Networks

본 논문은 ResNet의 후속 논문으로, Kaiming He 등 ResNet 저자들이 skip connection을 분석해 기존보다 개선된 ResNetv2를 제안한 논문입니다. skip connection을 적용한 backbone들에 대해 정리하고자 관련 논문들을 찾아보다 검색 중에 읽어보게 되었습니다. 그럼 리뷰 바로 시작해보도록 하겠습니다.

Abstract

Deep residual networks는 상당한 정확도와 수렴성을 보여주며 (당시에)extremely deep architectures의 한 종류로 급부상했습니다. 본 논문에서는 skip connections과 after-addition activation으로 identity mappings를 사용할 때 한 블록에서 다른 블록으로 forward/backward 신호가 직접적으로 전파되는 residual building blocks의 propagation 공식을 분석합니다. 뒤에 있는 Ablation study가 identity mapping이 중요함을 보여주며, 이를 통해 훈련을 더 쉽게 하고 일반성을 증대시키는 새로운 residual unit을 제안하는 동기를 제공합니다.

Introduction

ResNet은 수많은 Residual Units가 쌓인 구조로 이루어져 있습니다. Residual Unit은 다음과 같이 나타낼 수 있습니다.

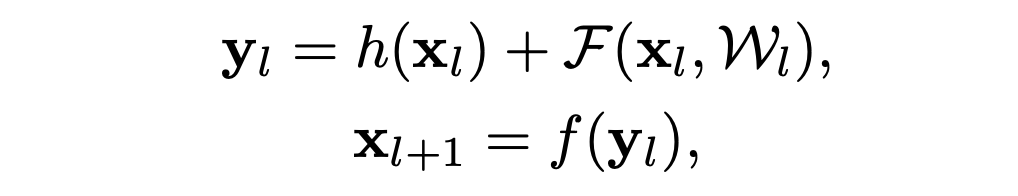
위 식에서 F는 residual function, h는 identity mapping, f는 ReLU입니다.

100층이 넘는 ResNet은 imagenet이나 MS COCO competition에서 SOTA를 달성했습니다. ResNet의 핵심 아이디어는 identity mapping h(xl) = xl을 사용하는 key choice를 통해 h(xl)에 대한 additive residual function F를 학습하는 것입니다. 이는 identity skip connection(shortcut)을 통해 구현됩니다.

본 논문에서는 residual unit 내부에서뿐만 아니라 아니라 전체 네트워크를 통해 정보를 전파하기 위한 direct path를 만드는 데 초점을 맞추어 deep residual network를 분석합니다. 저자들은 h(xl)와 f(yl)가 모두 identity mapping이라면, 한 유닛에서 다른 유닛으로 forward, backward pass로 신호가 직접적으로 전파될 수 있음을 도출합니다. 경험적으로는, 실험을 통해 모델 구조가 위의 더 조건에 더 가까울 때 일반적으로 훈련이 더 쉬워진다는 것을 보여줍니다.

skip connection의 역할을 이해하기 위해, 저자들은 다양한 종류의 h(xl)을 비교분석했습니다. 결과적으로는 우리가 알고 있는 resnet의 identity mapping h(xl) = xl이 가장 빠른 error 감소와 loss감소를 보여준다고 합니다(skip connection에 scaling과 1x1convolution을 한 버전 등을 비교했습니다. identity mapping은 별다른 연산을 취하지 않고 말 그대로 단순 덧셈을 한 skip connection입니다)

저자들은 identity mapping f(yl) = yl을 구성하기 위해, (ReLU와 BN등 이라고 합니다)activation function들을 기존의 “post-activation”와는 다른 weighted layer의 “pre-activation”라고 보고, 새로운 residual design을 만들게 됩니다. 그림을 참고하시면 쉽게 이해가 될 것인데, weighted layer 뒤의 BN와 ReLU를 앞으로 빼냈습니다.

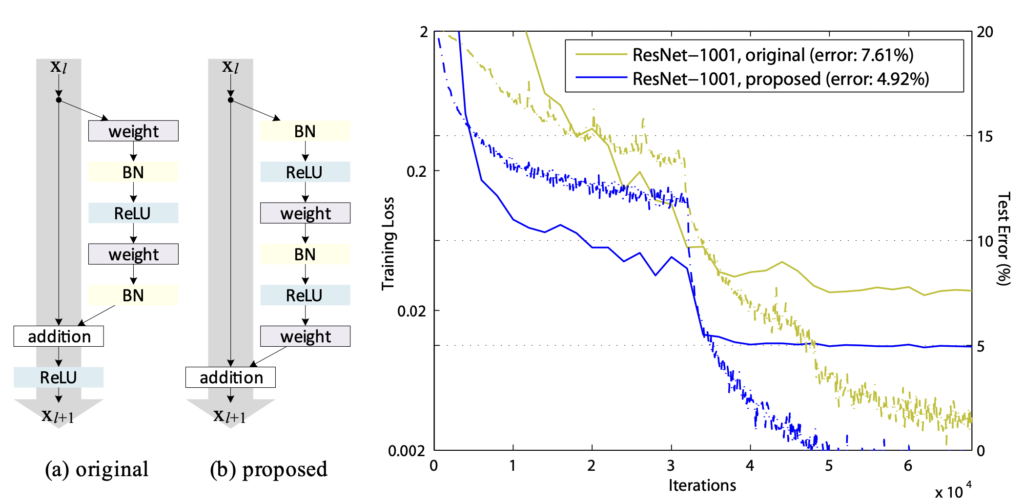
새로운 unit에 기반해 1000layer 모델을 만들어 CIFAR-10/100로 실험을 했는데, 기존 ResNet보다 훈련도 더 잘 됨을 확인할 수 있었습니다. ImageNet에 대해서는 200-layer ResNet으로 더 개선될 결과를 얻을 수 있었다고 합니다. 

Analysis of Deep Residual Networks

ResNet은 동일한 connecting shape의 block을 모듈화해서 쌓아 만든 구조입니다. 기존 Residual Unit을 다시 살펴보겠습니다.

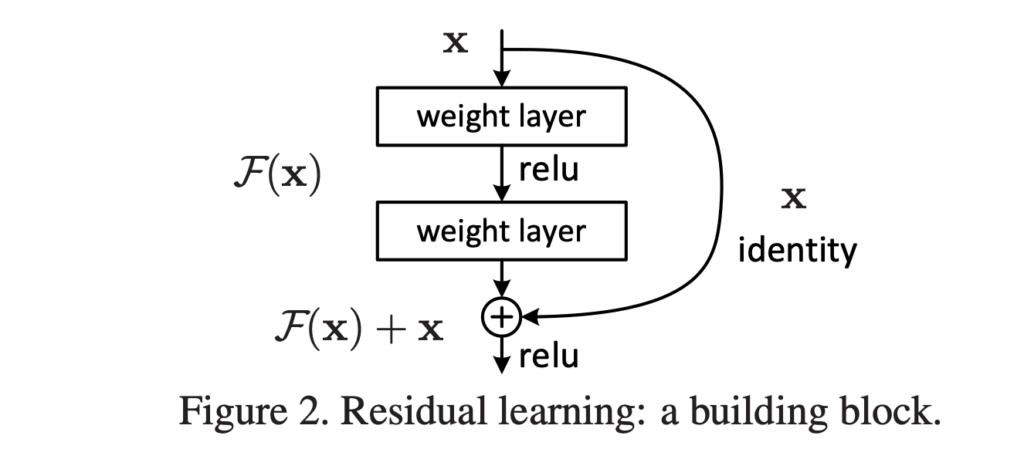
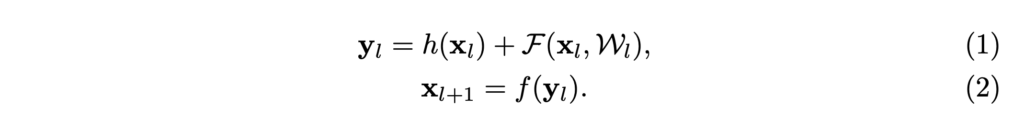
xl은 l번째 Residual Unit의 input feature, W는 l번째 Residual Unit의 weight와 bias들, F는 residual function(두 개의 3×3 convolution 등), f는 element-wise addition 이후의 연산(ReLU 등) 입니다.

f가 identity mapping xl+1 ≡ yl 이면, (1),(2)번 식에 대입해 다음과 같이 다시 쓸 수 있습니다.

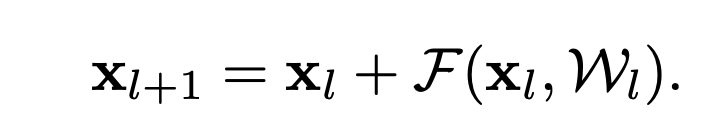
그럼 L번째 층 연산을 다음과 같이 표현할 수 있겠죠(수열의 점화식 -> 일반항 느낌으로 보시면 됩니다)

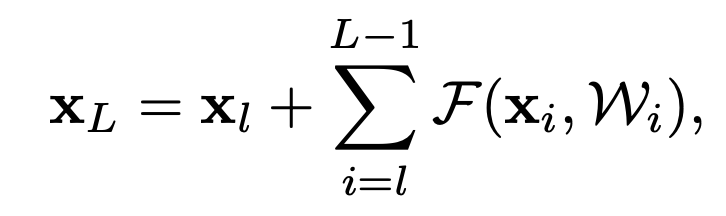
plain network는 feature X_L 이 일련의 matrix-vector products로 계산되지만, 위의 ResNet의 X_L은 이전 residual function의 output들의 합으로 계산된다는 점에서 차이가 있습니다. 이는 backpropagation에서 압도적인 이점이 있습니다.

Loss function을 ε라고 하면, 역전파 수식을 다음과 같이 전개할 수 있습니다.

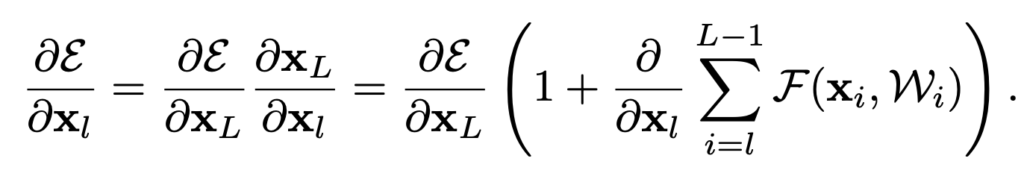
식을 보시면 gradient가 두개 항의 합으로 표현되는걸 보실 수 있습니다. 앞의 ∂ε/∂X_L은 weighted layer를 고려하지 않고 직접적으로 전파되고, 뒤의 ∂ε/∂X_L(∂/∂X_l ΣF(xi,Wi))는 weighted layer를 거쳐 전파됩니다. gradient가 0이 되려면 뒤쪽 항 ∂/∂X_l ΣF(xi,Wi)가 일괄적으로 -1이 되어야 하는데 (+1과 더해져 상쇄되어야 하기 때문입니다), mini-batch 안에서 그런 일이 일어나기는 힘듭니다. 바꿔 말하자면, weight가 작아지더라도 각 layer의 gradient가 사라질 일은 없으므로 gradient vanishing에 강해지게 됩니다.

4번 수식 표현은 identity mapping을 기본으로 합니다. (1) identity skip connection h(xl) = xl과, (2) f가 identity mapping이라는 점입니다. 이 직접적인 정보 전달은 위 그림에서 회색 라인에 해당합니다. identity skip connection에 대해 더 자세히 살펴보도록 합시다.

On the Importance of Identity Skip Connections

위의 h(xl)을 간단하게 수정해서, identity mapping이라는 조건을 깨봅시다. 

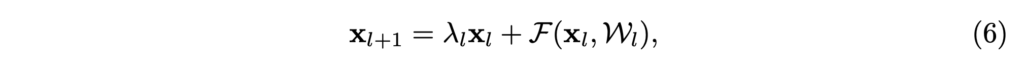
위 식을 재귀적으로 적용하면, 다음과 같은 일반항을 얻을 수 있습니다.

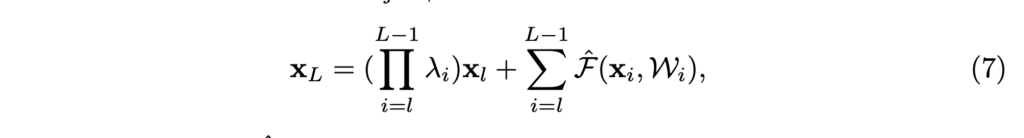
이 식의 backpropagation 식을 작성해보면 다음과 같습니다.

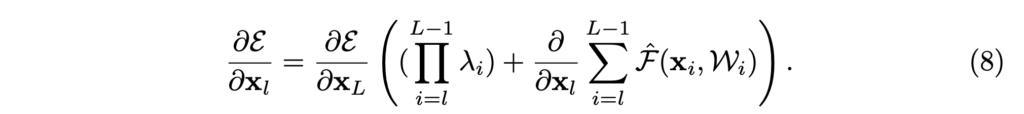
앞의 식과는 달리, 앞에 Π λi 항이 추가적으로 생겼습니다. 네트워크 깊이가 아주 깊어지게 된다면, 모든 i에 λi > 1 일 때는 이 값이 매우매우 커지게 되고, 모든 i에 λi < 1 일때는 값이 매우 작아져 원활한 정보 흐름을 방해하게 되겠죠. 저자들은 이런 요소들이 optimization difficulty를 야기함을 뒤의 실험에서 보입니다. identity skip connection을 단순히 h(xl) = λlxl로 수정했을 뿐인데도 이런 문제점이 나타났습니다. 저자들은 이것들보다도 더 복잡한 변형을 가하게 된다면(1×1 convolution이나 highway network의 gating 등) (8)번 수식과 마찬가지고 정보 전달을 방해하는 효과가 있을 수 있다고 합니다.

다음은 실험에 사용된 여러가지 skip connection입니다.

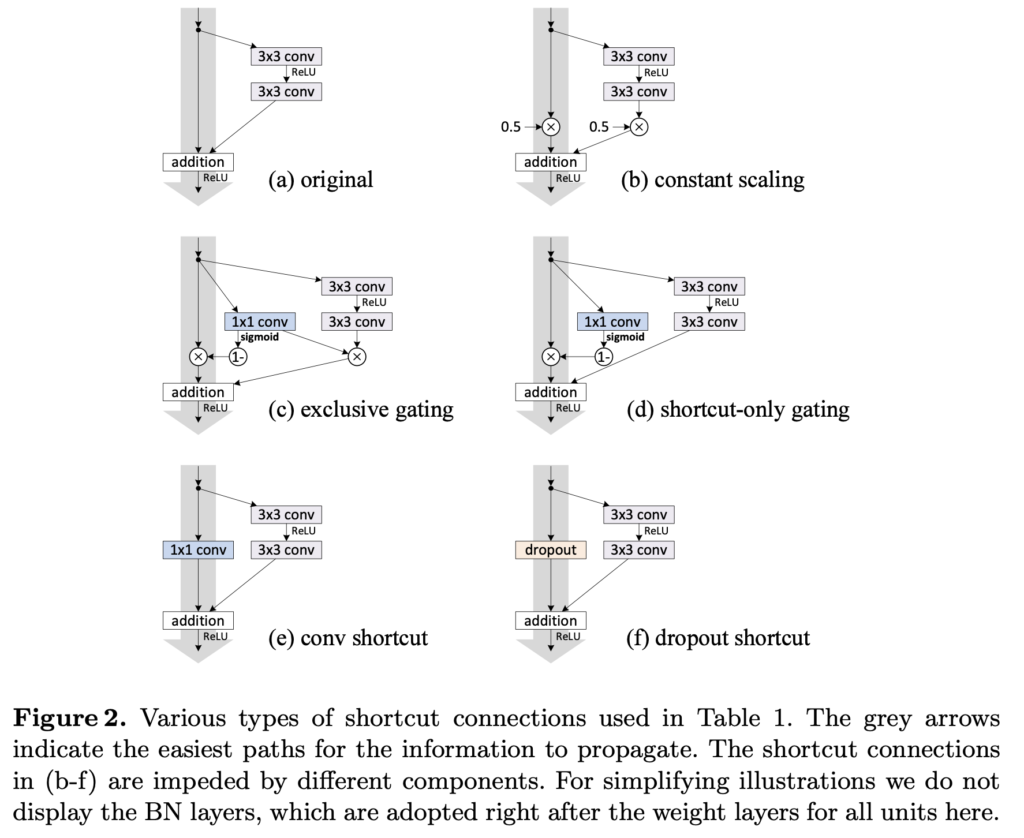
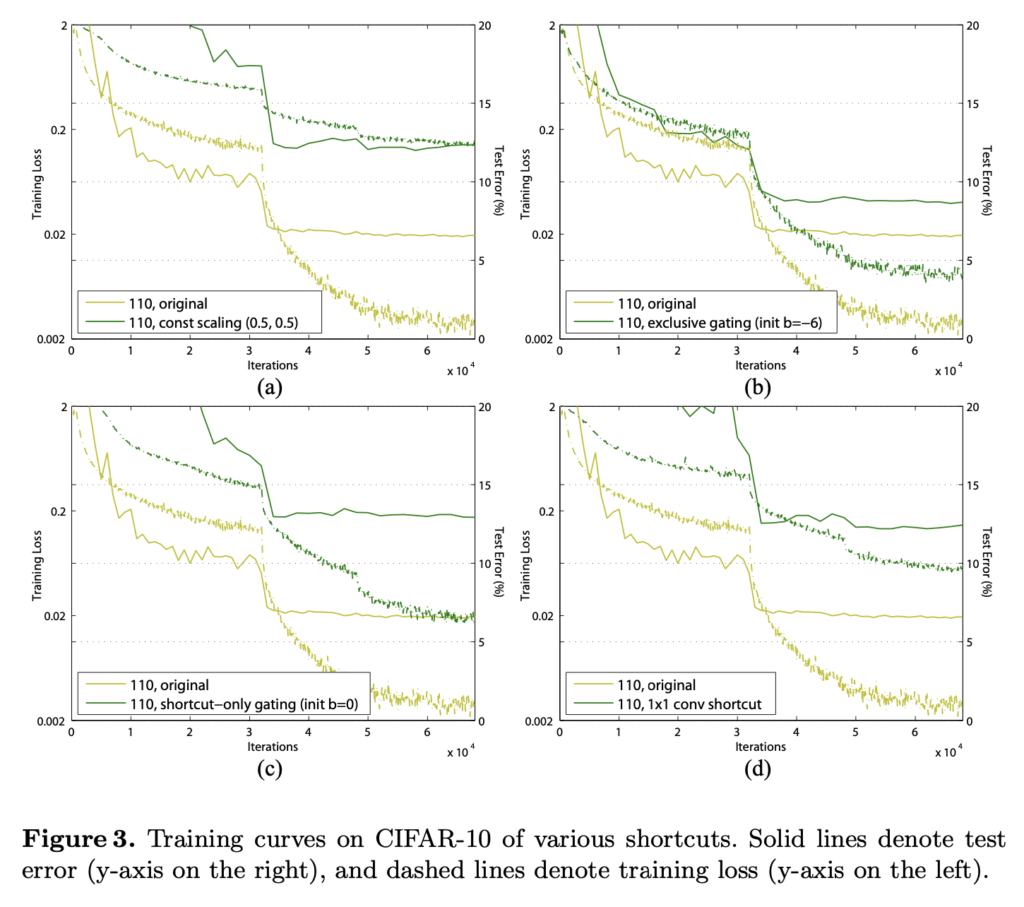
저자들은 CIFAR10에 ResNet110으로 실험을 진행했습니다(random요소를 최대한 없애기 위해서 5번씩 실험해서 가운데 성능들만 reporting했다고 합니다). ResNet110은 54개의 two-layer Residual Units로 구성되고, 상당히 깊기 때문에 최적화가 쉽지 않습니다. (a)는 original network이고, (b)에는 λ=0.5로 scaling을 적용했습니다. shortcut signal이 scaled down됐을 때 최적화에 더욱 어려움을 겪었다고 합니다. (f)에서는 0.5 비율로 dropout을 적용했고, 네트워크가 제대로 수렴되는데 실패했다고 합니다.

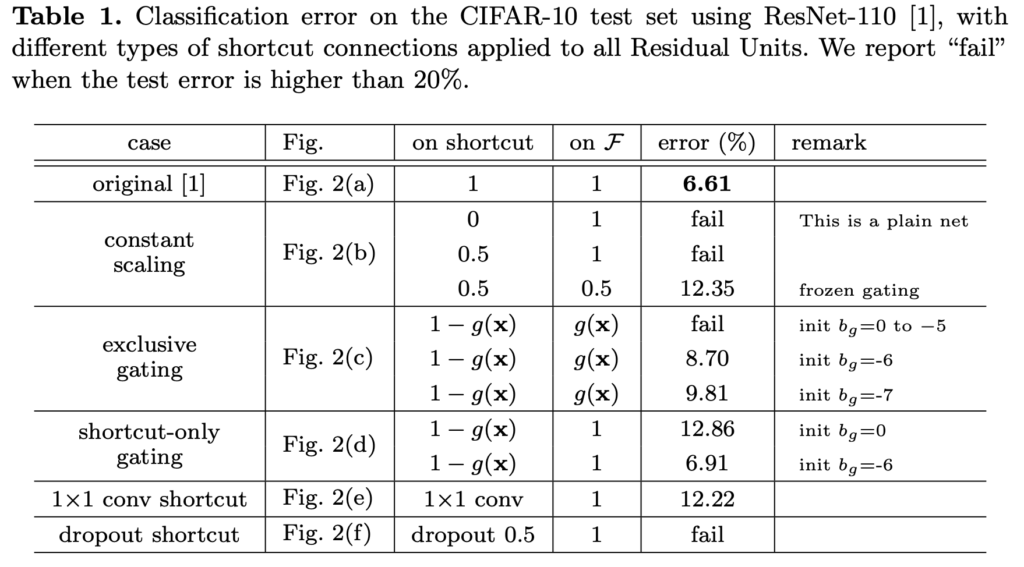
몇 가지 케이스를 살펴보겠습니다.

1×1 convolution은 ResNet 원문에서(ResNet34) 차원을 맞춰주기 위한 옵션 중 하나로 제시되었는데, 나쁘지 않은 성능을 보여주며 shortcut connection으로 사용하기에 나쁘지 않은 옵션이었습니다. 하지만 ResNet110쯤 되면서 계층이 깊어지게 되자 Table1에서 12.22의 error로 좋지 못한 성능을 보였고, Figure3의 (d)에서 확인할 수 있듯 training error도 높음을 확인할 수 있습니다. ImageNet에 대한 ResNet101에 대해서도 1×1 convolution shortcut은 비슷한 현상을 보였습니다.

Dropout Shortcut은 Fig2의 (f)에서 확인할 수 있는데, identity shortcut의 output에 적용되었습니다. 이 역시 좋지 못한 성능을 보였는데, 0.5ratio의 Dropout은 통계적으로 앞서 살펴보았던 λ=0.5의 scaling에 해당한다고 하며, 실제로 0.5로 scaling한것과 비슷한 양상을 보인다고 합니다. 이 역시 signal propagation을 방해한다고 볼 수 있습니다.

결국 정보 전파를 쉽게 하기 위해서는 인위적으로 다른 연산을(scaling, gating, 1x1conv, dropout 등) 끼워 넣는 것 보다는 shortcut connection을 통해 정보를 직접 전달하는게 가장 좋았다고 합니다. 저자들은 여기서 gating과 1×1 conv는 shortcut보다 더 많은 파라미터를 가지며 더 나은 표현력을 가질 수 있음에 주목합니다. 사실, 이런 방법을 사용하면 identity mapping과 동일하게 최적화될 수도 있는데 training error가 더 높은 것은 표현력이 부족해서라기보다는 최적화 문제에 있다고 해석합니다.

다음으로는 다양한 activation function에 대한 실험입니다. residual unit 내부를 어떻게 배치해야 할 것인지에 대한 실험으로 이해하시면 될 것 같습니다.

여기서는 ResNet110과 164-layer의 Bottleneck 구조(ResNet164)가 사용되었습니다. Bottleneck은 training time 이슈로 도입된 것인데, 1x1conv-3x3conv-1x1conv로 이루어졌습니다. 첫번째 1x1conv로 차원을 줄이고, 뒤쪽의 1×1로 차원을 원래대로 되돌려줍니다.

여러 실험 결과, (e)의 full-pre-activation 구조가 가장 좋은 성능을 보였습니다. 특히 BN을 pre-activation으로 도입하면 모델 정체의 정규화 효과가 커진다고 합니다.

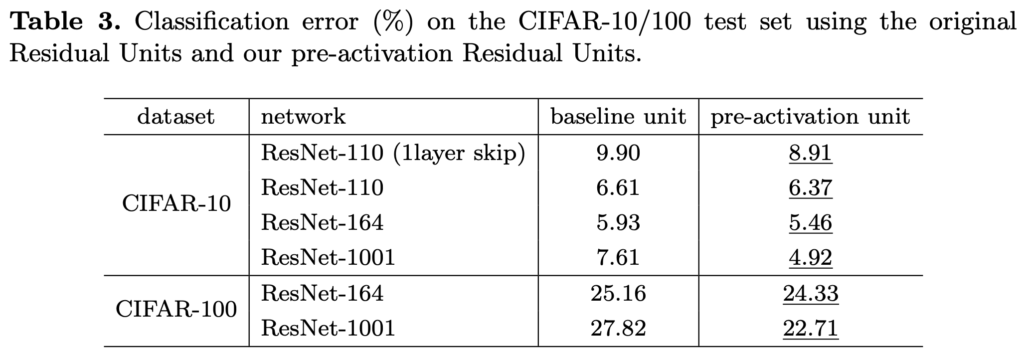
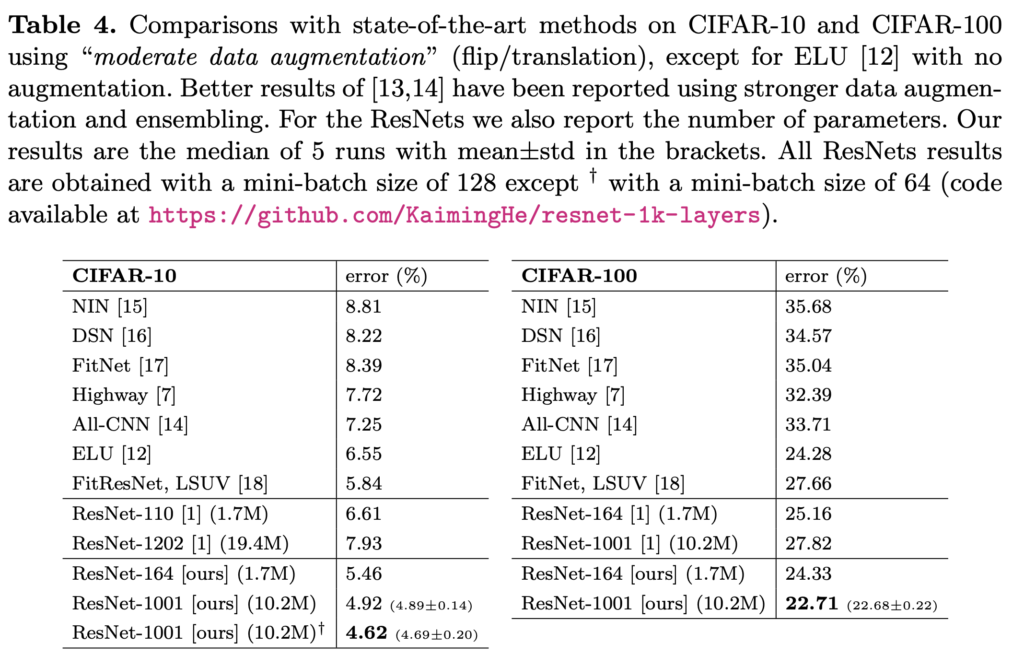
Results

CIFAR10/100에 대해서는, 작은 데이터셋의 regularization에 효과적인 테크닉(filter size, dropout등)을 써서 최적화시키지 않았음에도 단순히 깊이 쌓는 것만으로 좋은 결과를 내었습니다. ImageNet 데이터에 대해서도 개선된 성능을 보였습니다.

Conclusion

본 논문에서는 deep residual networks의 연결 메커니즘의 propagation 공식을 조사했습니다. 연구 결과, identity shortcut connection 과 identity after-addition activation은 정보 전파를 원활히 하는데 필수적이라는 가설을 도출했고, 개선된 ResNet을 제안하며 Ablation 실험 결과로 저자들의 가설을 뒷받침했습니다.

개인적으로 ResNet 논문에서 ‘skip connection을 추가해 해당 층이 처음부터 모든걸 학습하는 문제에서 단순히 잔차만 학습하게 되는 문제로 바뀌어서 네트워크 성능이 개선됐다’라고 설명하는 부분을 보고 이해가 잘 안되서 해당 공식을 수학적으로 분석해 보강한 논문인 줄 알고 찾아봤었는데, 세부적으로 새로운 구조를 제안해서 성능을 올렸던 논문이었습니다. 물론 backpropagation에 관한 분석이 있긴 하지만 더 자세한 분석이었으면 좋았을 텐데.. 아쉬움이 약간 남네요. 하지만 막연히 ‘skip connection을 추가하면 backward나 forward 계산할 때 신호 전달이 원활해서 학습이 잘 된다’ 정도로 이해하고 있었던 시점에서 이 논문을 읽으며 수식적으로 어떤 이점이 있는지 더 잘 이해하게 된 것 같습니다.

추가적으로 ResNetv2나 DenseNet 등등 개선된 버전의 백본이 더 많이 제안되었을텐데 최근 연구들에서 왜 여전히 백본으로 단순 ResNet이나 VGG등등을 사용하는지에 대한 궁금증도 남습니다. 많이 사용된 backbone들이어서 기존 연구들과 정확한 비교가 가능하기 때문일까요? 아직 읽어본 논문의 수가 절대적으로 부족해서 이런 의문들이 있는것 같은데, 차차 공부를 더 해가면서 이런 부분들을 채워나가야 할 것 같습니다.