안녕하세요, 양희진입니다.

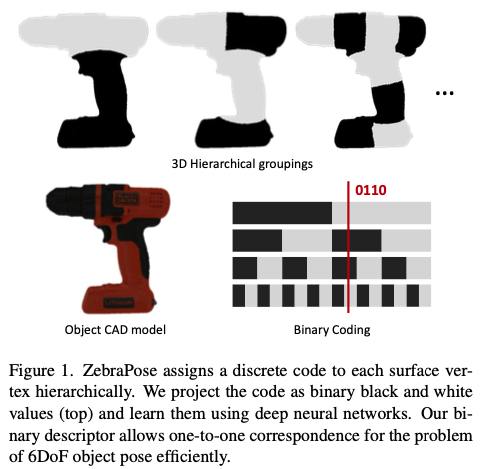
이번에도 6D pose estimation을 위한 방법론을 제안하는 논문을 리뷰했습니다. vertex의 개념을 이용하여 binary code representation을 사용하여 computational cost를 줄이면서, pose estimation의 효율적으로 이득봤다고 합니다. Zebra는 딱히 뜻은 없고 말 그대로 얼룩말을 뜻합니다. 위 fig(1)을 보면 마치 얼룩말에 있는 stripe를 연상시키는 것 같습니다. 제가 많은 논문을 읽어본 건 아니지만 이번 논문을 읽으면서 되게 참신한 발상이라고 느낀 논문입니다. 다루는 내용이 되게 많으니 재밌게 읽어주시면 감사하겠습니다.

리뷰 시작하겠습니다.

Abstract

2D에서 3D로부터 correspondence를 만드는 것은 6D pose estimation에서 핵심이라고 볼 수 있습니다. pose의 정확도를 올리기 위해서는, 충분히 학습된 dense map으로 sparse template을 대체를 해야합니다. Dense method는 occlusion이 존재하는 상황에 대해서 pose의 정확도를 향상시킬 수 있는 장점이 있습니다. 최근 연구에서는 언급한 성능 향상에 대해서 segmentation을 통해 증명을 하였다고 합니다. 이번 논문에서는 discrete descriptor를 이용하여 object의 표면을 dense하게 표현할 수 있다고 합니다. hierarchical binary grouping을 활용함으로써 물체의 표면을 효율적으로 encode할 수 있게 되었다고 합니다. 추가적으로 해당 논문에서 제안한 coarse to fine training strategy 를 통해 fine-grained correspondence를 예측할 수 있었다고 합니다. 마지막으로 예측된 code(binary)로부터 물체의 표면과 매칭을 하고 PnP solver를 통해 6D pose를 추정하게 됩니다. 실험은 LM-O, YCB-Video에서 진행을 하여 SOTA를 달성했다고 합니다.

Introduction

Correspondence 문제는 컴퓨터 비전 분야에서 매우 중요한 문제인데요, 하지만 이런 correspondence를 같은 도메인에서 찾는다는 것은 더 간단하지만 물체의 6D pose를 추정하려면 2D-3D correspondence가 필요합니다. 앞서 수행됐었던 연구들은 물체의 pose 추정을 위해서 depth map을 이용하여 이미지 픽셀과 3차원 표면의 점을 매칭시켜 매칭을 했습니다. 당연하게 cost와 setting의 복잡성으로 인해 depth 정보 없이 6D pose를 추정하는 것이 유리할 수 있습니다. 하지만, 단일 RGB 이미지만으로는 낮은 정확도를 보이면서 depth-base의 결과와 정반대의 결과를 보입니다.

최근에 CNN을 이용한 다양한 방법론들이 제안되었고 단일 RGB에서도 가능성을 보였습니다. 물체의 pose을 추정하기 위한 Correspondence-based setting은 주로 PnP(Perspective-n-Points) 알고리즘을 통해 최소 4개의 2D-3D 매칭점이 필요하게 됩니다. 그러므로 sparse method는 점을 뽑기 위한 수단으로 적용된다고 합니다. 하지만 이러한 방법론들도 실패에 마주하게 되는데요, 주로 물체의 viewpoint가 바뀔 때나, occlusion 하거나 texture가 부족할 때입니다. 저자는 이런 문제를 해결하기 위해 hand-crafted feature와 이미지 segmentation을 hierachical fashion을 통해 RGB 기반의 6D pose를 추정하기 위해 dense correspondence pipeline을 제안합니다. 표면을 효과적으로 encode할 수 있는 descriptor를 디자인 하기 위해 binary numeral system을 사용합니다. binary-based descriptor는 ORB를 통해서 얻을 수가 있습니다.

Zebrapose는 Dense 2D-3D correspondence의 매칭을 계층적 분류 작업으로 정의하는 RGB기반의 2-stage 접근 방식입니다. 저자는 6D pose 추정을 위한 일반적인 2-stage 접근 방식을 3가지 구성 요소로 나누어 설명을 합니다.

1. 3D vertex에 고유한 descriptor를 할당
2. 2D 픽셀과 3D vertices 사이의 dense correspondence을 예측
3. 예측된 correspondence를 사용하여 물체의 pose를 해결

저자는 다음과 같은 contribution이 있었다고 합니다.

• dense한 vertex descriptor를 효율적인 방식으로 할당하는 새로운 coarse한 surface에서 fine한 surface으로 encoding하는 방법으로 컴퓨터 비전 작업에서 사용되는 기존의 outlier filter를 활용
• 각 코드의 position에 대한 가중치를 자동으로 조정하는 새로운 계층적으로 학습 및 손실을 계산

ZebraPose를 사용하여 LM-O 및 YCB-V 데이터셋에서 해당 논문에서 SOTA를 달성했다고 합니다.

2. Related Work

2.1. RGB-based 6DoF Pose Estimation

Traditional Methods

feature descriptor의 발전과 함께 물체의 pose 문제를 풀기 위해서 2D-3D correspondence를 이용하여 PnP/RANSAC 과정을 거치게 됩니다. 하지만 texture가 부족한 상황에 대해서는 여전히 다루기 힘든 문제가 있는데요, 이러한 키포인트의 한계를 극복하기 위해 이미지의 gradient 정보를 활용하고 template matching 파이프라인 내에서 pose 추정 작업을 일반화하도록 제안했습니다.

앞선 방법론 이후 좀 더 개선된 방법은 통계적 학습 기반의 프레임워크를 적용하여 물체의 좌표와 물체의 라벨을 함께 regression함으로써 template searching 시간을 줄였습니다. 하지만 hand-crafted 방법론이라 요즘 사용하는 딥러닝의 방식에 못 미치는 결과를 보입니다.

End-to-End Methods

PoseNet에서는 CNN으로 카메라의 viewpoint의 regression을 시도한 최초의 논문입니다. 다음은 일반적으로 object detection과 pose regression과 연결하여 multi-object의 pose를 추정할 수 있게되었습니다. 그 당시에는 pose regression에 적합한 rotation의 representation을 찾는 것이 문제였고, 일반적인 retation에 대한 parameterization은 유클리드 공간을 채울 수 없었다고 합니다. SSD6D에서는 회전 공간의 discretization을 통해 회전을 다루는 방식으로 복잡한 parameterization을 피하면서 회전에 대한 추정을 classification 문제로 처리하였습니다. 신경망 학습을 위해 quaternion 또는 Lie algebra를 이용한 parameterization에 비해 장점을 보여주는 6차원의 회전에 대한 representation을 제안하고 이러한 representation을 바탕으로 여러 direct regression에 활용되게 됩니다.

이와 동시에, 학습 프레임워크를 제시하기 위해 RANSAC과 PnP 모듈을 통합하기 위한 여러가지 방법론들이 제안 되었습니다. 이를 위해서는 좋은 초기화 방법과 복잡한 학습 방법이 필요하게 됩니다. 이런 이유로 물체의 pose를 추정에는 적용되지 않는 차별화된 RANSAC의 변형된 방법을 사용하게 됩니다. 또, pose에 대한 metric을 반영하는 loss function을 사용하여 PnP 문제를 해결하는 네트워크를 제안합니다. 이와 더불어 딥러닝의 성장과 함께 새로운 신경망 기반의 renderer의 성장과 함께 새로운 방법들도 많이 제안되었습니다.

Indirect Methods with Deep Learning

시간이 지남에 따라 다양한 모듈을 통합하여 end-to-end 방식이 발전되어 왔지만, 이러한 방식의 성능은 일반적으로 geometric method와 indirect 방식에 비해 성능이 떨어집니다.

gemetric method로는 learning feature와 geometrical feature의 fitting을 결합한 metric을 학습으로 사용하여 triplet loss를 통해 함축적인 pose representation을 학습하고 최종적으로 pose space에서 가장 가까운 이웃을 찾는 방법론이 있습니다.

indirect method로는 일반적으로 2D-3D correspondence를 추정하고 PnP/RANSAC을 사용하여 물체의 pose를 추정합니다. 대표적으로 PVNet에서 물체의 sampling된 키포인트에 대해 dense pixel-wise voting 방식으로 키포인트를 예측하여 LINEMOD에서 높은 recall을 달성한 이력이 있습니다. 하지만 이러한 sparse 2D-3D correspondence 방법의 치명적인 점은 occlusion에 대해서 키포인트의 예측 정확도가 떨어진다는 점입니다. 이러한 문제를 해결하기 위해 Pixel-wise의 dense 2D-3D correspondence를 예측하는 방법이 있습니다.

2.2. Surface Encoding

binary surface encoding은 reconstruction 분야에서 수년 동안 사용되어진 기법이라고 합니다. 해당 기법을 사용하기 위해 비디오 프로젝터 여러 개의 연속적으로 refine된 binary fringe 패턴으로 장면을 비춥니다. 다양한 stripe 패턴의 구성은 표면에 대한 점의 encoding을 제공하게 됩니다. 여러 분류 문제를 해결하기 위해 사용되는 surface coding은 안정적이면서 효과적인 것도 입증이 되었다고 합니다. 이를 통해, 신경망은 분류 문제를 해결하는 것에 적합하다고 판단하고, 적용을 했다고 합니다. pose 추정 도메인에서 dense 2D-3D correspondence을 추정하려면 각 3D corresponding 포인트에 고유한 descriptor를 할당해줘야 합니다. 이 논문에서 제안하는 방법은 dence 2D-3D correspondence를 hand-crafted code를 통해 학습하는 방법입니다. 물체의 표면을 coarse한 것부터 fine한 것까지 encoding합니다. bit가 고유한 3D-correspondence을 정의할 수 있을 정도로 즉 fine해질 때까지 반복적으로 물체의 surface를 분할시킵니다. 이런 계층적 수준을 통해 correspondence를 점진적으로 세분화할 수 있습니다.

3. Method: ZebraPose

3.1. Coarse to Fine Surface Encoding

물체의 surface에 대한 CAD 모델과 그 vertex v_i \in R^3 (여기서 i는 vertex의 id를 나타냄)이 주어지면, 각 v_i를 vertex code c_i \in N^d(여기서 d는 vertex 코드의 길이)로 representation 하려고 합니다. 주어진 3D 물체의 표면에 대한 vertex의 위치를 기준으로 해당 encoding을 정의해야 coarse learning에서 fine learning을 할 수 있게 됩니다. 이를 위해 10진수가 아닌 숫자 체계로 코드를 구성했다고 합니다.

lower radix와 더불어 encoding을 numerical system으로 정의하는 것은 매우 효과적이고 쉽게 점을 coarse에서 fine grouping으로 representation을 할 수 있다고 합니다. 앞서 d는 코드의 길이라고 설명을 했었는데, 이는 vertex들의 grouping을 위해 d번의 iteration을 의미한다고 합니다. j 번째의 iteration에서 그룹 G_j의 집합은 r^j 그룹으로 구성됩니다. 여기서 G_0는 물체 전체의 vertex 중 한개의 그룹만 존재하며 이를 initial group으로 정의할 수 있습니다. j>1인 G_j는 G_{j-1}의 각 그룹을 r그룹으로 분할하여 얻습니다. 그룹핑을 반복하면서 각 vertex v_i는 j 번째 그룹핑에서 속하는 그룹에 따라 class id m_{i,j}가 할당되며, 마지막으로 각 vertex는 각 그룹핑 과정의 class id를 stack하여 각 vertex code에 d자리 숫자를 할당합니다. 해당 representation은 모든 3D 물체에 대해 저장되고 고정됩니다. 각 그룹의 vertex는 동일한 code를 공유하게 되고 look-up table을 구축하여 code를 G_d의 각 중심에 매핑하고 이를 바탕으로 2D-3D correspondence를 구축하고 pose solver를 통해 최종적으로 R, T를 계산합니다.

3.2. Choice of the Radix for Vertex Code

앞서 다루었던 grouping에 따르면 총 클래스의 수가 K 라고 할 때(K=r^d), 분류 문제를 해결하기 위해 o logit을 이용하여 map을 학습합니다(o=r \cdot d).

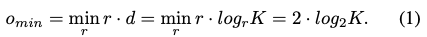
eq(1)은가장 많은 수의 클래스를 학습하면서 결과물의 수를 최소화하는 식을 의미합니다. 해당 식을 이용하여 네트워크의 layer를 최소화하기 위해 선택할 수 있는 가장 좋은 양의 정수 r은 2와 4였다고 합니다. 해당 값은 positive 또는 negative로 분류되기 때문에 cross entropy를 사용할 필요가 없게 됩니다. 따라서, r=2를 사용하면 최적의 output layer수로 \log_{2}K를 얻을 수 있습니다.

GPU 메모리의 메모리 사용량이 줄어드는 장점 외에도 binary vertex code를 사용하면 높은 정확도를 얻을 수 있기 때문에 binary-based vertex code를 적용했고 또한 이러한 장점은 실험을 통해 증명하였다고 합니다.

3.3. Rendering the Training Labels

이미지 내의 각 픽셀은 3차원 물체에 대한 vertex에 대응되게 됩니다. 네트워크에서는 class id를 결국 예측해야 하는데, 각 그루핑(grouping) 과정으로 얻은 vertex로 부터 class id 가 할당되어 집니다. 하지만 여전히 이미지와 주어진 정보로부터 학습을 위해 class id를 렌더링 하는 것을 필요로 하게됩니다. 그래서 저자는 이러한 목적을 가지고 vertex의 class id 이용하는 것이 아닌, mesh에 대한 face의 class id로 바꾸기 위해 다음과 같은 기준을 정하였다고 합니다.

• 만약 face에 대한 2개의 vertex가 같은 class id를 가지고 있는 경우 → 해당 face는 그 class id를 할당
• 그외로는 모두 첫 번째 vertex의 class id를 할당

위와 같은 과정을 각 그룹에 대한 학습 라벨인 class id가 전부 생성될 때까지 d번 반복한다고 합니다.

3.4. Network Architecture

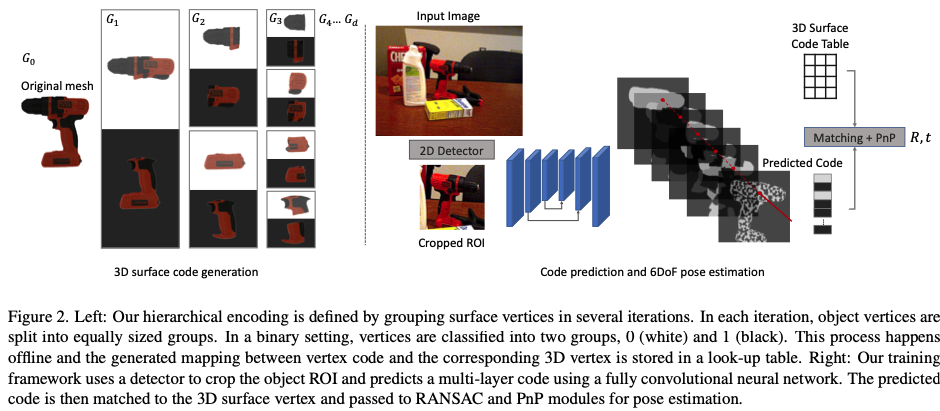
ZebraPose의 전체적인 네트워크 구조는 fig(2)와 같습니다.

앞서 최적의 radix를 2로 선정을 하였습니다. 이를 고려하면서 저자의 목표는 binary 값으로만 2^d영역으로 분류를 하는 것으로 하였다고 합니다. 물체의 pose에 대한 annotation을 사용하여 라벨을 이미지 좌표에 계층화된 black&white map으로 렌더링하여 학습을 진행했다고 합니다. code 및 visible mask 예측을 위한 objective learning map의 크기는 d+1로 binary 라벨이 되게 됩니다. 여기서 d는 binary vertex code의 길이, 1은 object mask 채널로 이해했습니다. 그리고 encoder-decoder 과정에서는 단일 decoder를 사용하여 그대로 d+1의 출력을 하도록 했고, discrete vertex code representation을 사용하기 위해 최종 output 확률을 반올림을 해주었다고 합니다.

[ discrete vertex code representation은 vertex를 고유하게 식별할 수 있고, 항상 동일한 코드를 할당할 수 있으며 binary code 보다 짧은 길이로 vertex를 representation을 할 수 있으므로 효율성이 좋다고 합니다. ]

Frame의 픽셀 당 code를 정확하게 예측하기 위해, 물체의 RoI만 처리하기 위해 2D detector로부터 검출된 결과를 Crop&Resize하여 고정된 너비로 RoI를 만들어서 학습 과정 때 target vertex code map에 정확하게 적용될 수 있도록 설계를 하였습니다.

3.5. Hierarchical Learning

encoding은 계층적인 구조로 되어있기 때문에 coarse한 code로부터 fine한 code까지 모두 학습하도록 하였습니다. 따라서, 예측은 coarse한 grouping부터 fine한 grouping까지 다양한 단계로 학습이 되고 계층적 수준에서 각 위치에 대한 error histogram을 사용하여 error의 정도에 따라 hamming-based loss에 가중치를 부여하도록 하였습니다. 최종 total loss까지 어떻게 구하는지 알아보도록 하겠습니다.

Mask loss

background와 물체의 영역을 분할하기 위해 visible mask를 예측하도록 하였는데, 간단하게 예측에 대한 확률들을 sigmoid에 전달하고 L1 loss를 사용하여 L_{mask} 를 사용합니다.

Hamming Distance

CNN은 RoI내의 픽셀에 대해 binary vertex code 확률인 \hat P를 출력하고 이 \hat P를 반올림하여 예측된 discrete binary code \hat b 를 구하게 됩니다. \hat b와 b(GT)가 주어졌을 때 hamming distance(Hamm)은 GT와 다른 \hat b의 수를 세어 정의하였다고 합니다. 즉 b와 다른 만큼 distance가 커지게 되니까 loss가 커지는 구조인 것 같습니다. 이렇게 Hamm을 사용하면 어느 position에도 유리하지 않게(공평하게) 명시적으로 고려하지 않고 error를 계산할 수 있게 됩니다.

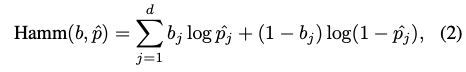
eq(2)는 binary cross entropy를 사용하여 distance에 대한 activation function으로 사용하였다고 합니다. 식에 대한 notation에서 b_{j}를 한 번 살펴보면 b에서 j 번째 bit를 의미하고, 이는 j 번째 vertex grouping 과정에서 생성된 bit를 의미합니다. p도 동일하게 적용되므로 이해하실 거라 생각합니다.

Active bits

binary vertex code b의 low-bit는 coarse correspondence, high-bit는 더 fine한 추정치를 정의합니다. 초기의 학습 단계에서는 network는 coarse한 correspondence에 중점을 두고, fine bit에 대한 error가 더 큰 문제가 있었습니다. 이러한 문제를 해결하기 위해 저자는 모든 bit에 대한 error histogram을 구성하여 확인하고, coarse bit에만 치중하지 않고 adaptive하게 가중치를 부여하도록 설계하였습니다. 이와 같이 설계를 한다면 학습이 진행되면서 더 fine한 bit에 보다 더 많은 가중치를 받도록 유도를 하였다고 합니다. 저자는 training step t에서 error histogram을 통해 다양한 bit의 error를 확인하고 아래와 같은 eq(3)을 정의합니다.

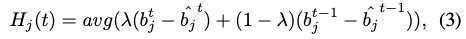
eq(3)을 살펴보면 먼저 \hat b_{j}^t는 t에서 예측된 binary vertex code를 의미하고, \lambda는 상수를 의미합니다. avg를 사용하여 예측된 물체의 mask 내의 모든 픽셀에 대한 b_{j}^t, \hat b_{j}^t의 평균 차이를 미니 배치 단위로 계산하여 오류의 비율을 구하는 방법을 사용했다고 합니다.이와 같은 방법으로 즉, 학습 중에 이전(t-1)의 histogram과 현재(t)이 주어지면 histogram을 업데이트하는 방식을 사용합니다.

Hierarchical loss

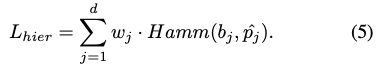
앞서 histogram을 기반으로 가중치를 계산하고 이를 Hamming distance와 함께 사용하여 eq(5)의 hierarchical loss를 구성하게 됩니다.

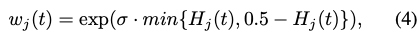
eq(4)에서 w_j를 정의합니다. \sigma는 상수이고, exponential을 사용하여 t에서 j 번째 bit에 대한 가중치를 soft하게 정의하도록 설계하였다고 합니다. soft라는 말이 이해가 잘 안 돼서 찾아봤는데 exponential 함수는 일반적으로 값이 작은 차이에도 큰 가중치를 부여할 수 있어 모델의 비선형성 유지등의 효과를 얻을 수 있다고 합니다. 이렇게 hierarchical loss를 정의하였는데, 이는 학습 중에 coarse bit에서 fine bit으로 자동으로 변경되는 active bit에 주로 집중할 수 있도록 작동한다고 합니다.

Total loss to train the CNN

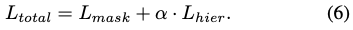
하이퍼파라미터 \alpha를 사용한 L_{hier}와 L_{mask}를 사용하여 가중치를 부여하는 식으로 전체적인 loss식은 eq(6)으로 나타낼 수 있습니다. 이때 \alpha는 배경으로 예측되는 픽셀은 0이 되도록 합니다.

Pose estimation

앞선 section들은 descriptor를 생성하는 방법과 CNN을 이용하여 예측하는 방법들을 다루었는데요. 최종적으로 pose estimation을 수행하기 위해서는 예측을 통해 얻은 code와 visible mask을 이용하여 3D model encoding을 한 3D surface code table과 매칭시켜줘야 합니다. 하지만 일반적으로 dense correspondence를 만들어줘야 하는 방법과는 다르게 이 논문에서 사용하는 compact한 representation을 사용하여 surface vertex와 descriptor space 사이에 bijective correspondence도 가능하다고 저자는 설명을 하는데요. 다행히도 이 말에 대한 설명을 해주었습니다. 물체에 대한 surface에서 벗어날 수 있는 regression된 3D point와는 다르게 추정된 3D correspondence는 항상 3D vertex를 reference하게 되므로 pose solver의 매칭이 좀 더 쉬워지게 됩니다. 그래서 매칭을 위해 추가적으로 look-up table을 사용하였다고 합니다. Prograssive-X solver를 사용하여 최종 R, T를 계산하였다고 하는데, 찾아보니까 최적화 문제를 푸는데 사용되는 방법이라고만 이해를 하였습니다.

4. Experiments

ZebraPose는 LM-O, YCB-V에서 실험을 진행하였다고 합니다.

Ablation study

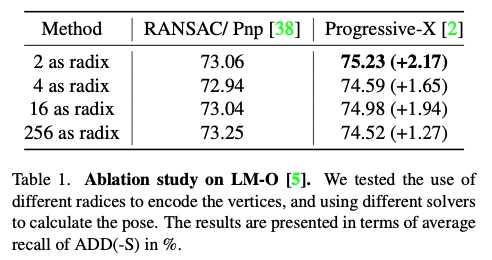
최적의 최적의 radix 앞서 설명할 때 구하고 solver에 대한 성능을 비교한 표 입니다.

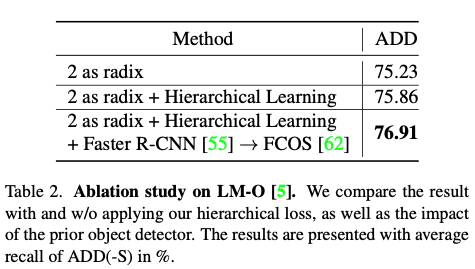
radix를 2로 고정시키고 계층적인 학습을 적용한 것에 대한 성능을 비교하고 또한 기존의 Faster R-CNN에서 anchor-free 방법론 중 FCOS를 적용한 detector에 대한 성능 평가입니다.

Comparison to State of the Art

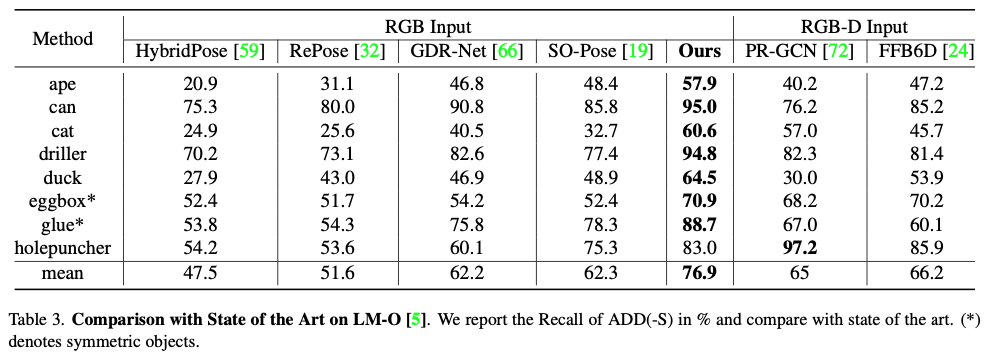
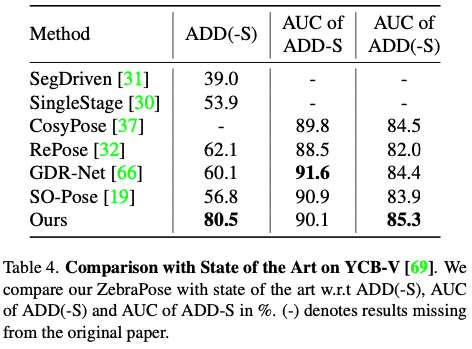
마지막으로 표(3), (4)에서 다른 모델과 비교하면서 SOTA를 달성함을 실험을 통해 정량적으로 나타낸 표입니다.