안녕하세요, 양희진입니다.

이번에도 베이스라인을 위해 6D Pose Estimation에 관련된 논문을 리뷰해봤습니다. 최근 BOP 챌린지에서는 GDR-Net++이 우수한 성능을 달성한 이력이 있어 먼저 이전 논문인 GDR-Net을 읽게 되었습니다.

Abstract

단일 컬러 이미지로부터 6D Pose Estimation을 하는 것은 컴퓨터 비전에서는 근본적인 문제라고 할 수 있습니다. 최근에는 딥러닝이 발전하면서 indirect strategy와 같은 방법으로 해결을 합니다. indirect strategy란, 처음에 2D-3D 간의 correspondence를 생성하는데 이는 이미지 평면의 좌표와 물체의 좌표계간의 correspondence를 의미하게 됩니다. 이후 PnPfRANSAC 알고리즘을 적용하는 것을 의미합니다. 저자는 이런 2-Stage 파이프라인으로 진행하는 게 end2end trainable이 불가능하기 때문에 다양한 pose가 필요한 작업에 활용하기는 어렵다고 말합니다. direct regression 방법론은 geometry-based 방법론 보다 성능이 떨어집니다. direct regression 같은 경우 CNN을 통한 방법이라고 생각하시면 좋을 것 같습니다. 해당 방법론을 통해 end2end로 학습은 가능하지만 대량의 학습 데이터와 복잡한 네트워크 구조가 필요하다고 생각이 들고 또한 geometry-based 방법론은 상기 indirect strategy를 의미하는 것으로 이해하시면 될 것 같습니다. 해당 논문에서는 direct 방식과 indirect 방식에 대해서 심층적인 고찰을 통해 dense correspondence-based intermediate geometric representation으로부터 end2end 방식으로 6D pose를 학습하는 간단하면서도 효과적인 GDRNet을 제안하게 됩니다.

1. Introduction

카메라에 대한 물체의 6D Pose 를 추정한다는 것은 3D rotation과 3D translation을 추정한다는 것입니다. 대부분의 기존 방법론들은 depth 데이터에 의존하지만 monocular 방식으로는 상당히 뒤처지는 게 현실입니다. 그럼에도 불구하고 딥러닝의 발전으로 인해 CNN과 같은 Network 구조를 통해 monocular 6D pose estimation의 정확도와 강인함은 지속적으로 개선을 하고 있는 추세입니다. 최근에는 depth 데이터에 의존하는 방법론보다 능가하는 성능까지 발전을 한 상태라고 합니다.

monocular 데이터에서 6D pose를 예측하기 위한 다양한 전략들이 제안되었는데, pose를 위한 embedding space 학습하거나 3D 회전 및 이동의 direct regression 등이 있습니다. 이러한 방법들은 일반적으로 성능이 좋지만, 6D pose를 추정하기 전에 2D-3D correspondence를 생성하는 방식과 비교할 때 정확도가 떨어지는 경우가 더 많습니다.

이와 달리 후자의 방법은 일반적으로 PnP/RANSAC 알고리즘의 변형을 통해 6D pose를 풀어나가는 방법입니다. 이러한 패러다임은 좋은 estimation 값도 제공하기는 하지만 아래와 같은 단점도 있습니다.

• 일반적으로 correspondence regression를 위한 보조(?)의 역할로써 목표로 학습되는데, optimization 후 실제 6D pose error를 필수적으로 반영하지는 않습니다
  • 실제에서 2D-3D의 correspondence는 완전히 다른 pose를 설명하면서 동일한 average error를 가질 수 있습니다.
• 추정된 6D pose와 관련하여 차별화 되지 않기 때문에 학습에 제한이 있습니다.
  • 예를 들어, 해당 방법은 데이터와 pose사이의 신호를 얻기 위해 pose의 계산이 완전히 차별화 되어야하기 때문에 라벨이 지정 되지 않은 실제 데이터로부터 self-supervised learning과 결합할 수 없습니다.
• Dense correspondence을 처히라 때 반복적인 RANSAC 과정은 매우 많은 시간이 소요되게 됩니다.

정리를 해보면, 2D-3D correspondence에 기반한 방법이 6D pose estimation 분야를 주도하고는 있지만, 문제를 두 단계로 분리하고 그 중 하나만으로 구분할 수 없기 때문에 여전히 단점을 보입니다. 따라서 PnP/RANSAC 과정을 통해 역전파를 활성화하기 위해 많은 노력을 했다는 것 입니다. 하지만 이것은 scene coordinate를 잘 초기화하기 위해 복잡한 학습 전략이 필요하거나 미리 정의된 키포인트의 sparse correspondence만 처리할 수 있게 됩니다. 그래서 sparse correspondence에 대한 PnP를 approximation하기 위해 PointNet를 활용하는 것을 제안합니다. 해당 방법론은 잘 작동하는 것으로 입증되었지만, PointNet은 이미지 픽셀을 기준으로 correspondence이 구성된다는 사실을 무시하기 때문에 성능이 크게 저하되는 경향이 있다고 합니다.

저자는 2D-3D correspondence를 설정하는 동시에 최종 6D pose 추정치를 완전히 미분 가능한 방식으로 계산하여 해당 한계를 극복하는 것을 제안하게 됩니다.

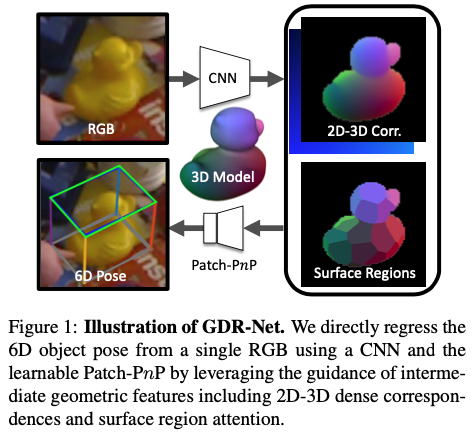
핵심은 correspondence가 이미지 공간에서 구성된다는 팩트를 활용하여 PnP optimization을 통해 학습하는 것을 제안하고, 이전의 모든 방법론들 보다 성능이 크게 향상되었음을 보입니다.

저자는 다음과 같은 contibution을 했습니다

• indirect 6D pose regression의 핵심 요소를 다시 살펴보고 pose 파라미터에 대한 적절한 representation을 선택한다면 direct regression에 기반한 방법론이 correspondence 기반 indirect 방법론에 비해 경쟁력 있는 성능을 달성함
• dense correspondence 기반 intermediate representation의 기하학적인 가이드를 활용하여 간단하면서도 효과적인 Geometry-guided Direct Regression Network(GDR-Net)을 제안함

2. Related Work

Indirect Methods

가장 널리 사용되는 접근 방식은 2D-3D correspondence를 설정한 다음, RANSAC 기반 PnP 알고리즘의 변형을 사용하여 6D pose를 푸는 데 활용합니다.

Direct Methods

2D-3D correspondence을 활용하는 indirect 방법이 현재 더 나은 성능을 보이고 있지만, pose 추정을 다시 차별화 해야하는 많은 테스크에서는 직접 사용하기에는 적절하지 않습니다. 따라서 제안된 방법론들은 point matching loss를 활용하거나 각 component에 대해 별도의 loss 조건을 걸어 6D pose를 직접 regression 합니다.

Differentiable Indirect Methods

PnP/RANSAC을 차별화 하려고 시도하고 있는 추세입니다. 최근 제안된 논문에서는 예측 분포에 기반한 hypothesis 공유를 통해 RANSAC을 적용할 수 있는 새로운 차별화 방법이 있습니다. 이러한 접근 방식은 scene 좌표의 초기화가 잘 이루어질 것으로 기대하기 때문에 복잡한 학습 전략이 필요합니다.

PnP의 경우, Implicit Function Theorem을 사용하여 pose loss에 대한 analytical gradient를 계산할 수 있습니다. 하지만, 학습과 추론 모두에 PnP/RANSAC 과정이 필요하기 때문에 correspondences가 너무 많은 경우 당연히 computational cost 또한 많이 드는 단점이 있습니다. 이를 극복하기 위해 고정된 sparse 2D-3D correspondences 세트에서 6D pose를 추론하는 방법을 학습하는 PointNet기반 아키텍처로 PnP 단계를 학습하려고 시도합니다.

3. Method

RGB 이미지 I와 N 개의 물체 \mathcal O 세트와 해당 3D CAD 모델 \mathcal M이 주어지면 우리의 목표는 I에 존재하는 각 물체 \mathcal O에 대해 카메라에 대한 물체의 6D pose P=[R|t]를 추정하는 것입니다.

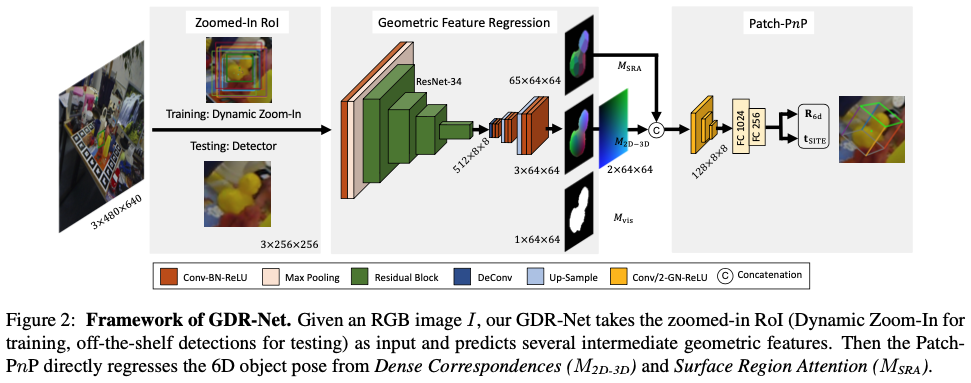
그림2는 GDR-Net의 프레임워크를 나타낸 그림입니다. 처음 RoI를 할 때는 detector를 사용하여 물체를 찾습니다. 각 RoI에 대해 확대하고 네트워크에 넘겨주면서 여러 intermediate geometric feature map을 예측합니다. 마지막으로 dense correspondence 기반의 intermediate geometric feature에서 연관된 물체의 6D pose를 direct regression을 수행합니다.

3.1. Revisiting Direct 6D Object Pose Estimation

Parameterization of 3D Rotation

3D 회전을 설명하기 위해 여러 가지 다른 parameterization을 사용할 수 있습니다. 많은 representation이 모호성을 나타내기 때문에 R_i와 R_j가 R_i \ne R_j로 동일한 회전을 설명하기 때문에 대부분의 과정에서는 학습을 돕기 위해 고유한 parameter에 의존하게 됩니다. 따라서, unit quaternion, log quaternion, Lie algebra 기반 벡터가 일반적으로 선택된다고 합니다.

그럼에도 불구하고 3D회전에 대해 4차원 이하의 모든 representation은 Euclidean space에서 불연속성을 갖는 것은 이미 입증되었습니다. 회전에 대해 regression을 수행할 때 불연속성에 가까운 error가 발생하고 이 error값은 종종 상당히 커지게 되는 현상이 발생하게 됩니다. 이러한 한계를 극복하기 위해 SO(3)에서 R에 대한 새로운 6-dimensional representation을 제안하였으며 이 또한 유망함이 입증되었다고 합니다.

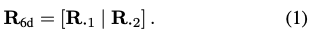
위의 내용을 구체적으로 살펴보면, R_{6d}로 표현하고 R 의 처음 두 열로 정의하면 식(1)을 얻을 수 있습니다.

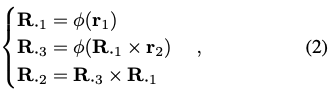
6차원 벡터 R_{6d}=[r_1|r_2]가 주어지면 회전 행렬 R=[R_1|R_2|R_3]은 식(2)을 통해 계산을 할 수 있게 됩니다. 이때 \phi(\bullet)는 vector normalization operation을 나타내게 됩니다. 해당 representation의 장점을 고려하면서 해당 테스크에서는 R_{6d}를 사용하여 3D 회전을 parameterization 했다고 합니다. 저자는 네트워크가 R_{a6d}를 예측하도록 합니다. R_{a6d}는 allocentric representation을 의미하게 됩니다. 해당 표현을 사용하면 물체의 3D translation을 해도 viewpoint-invariant하기 때문에 해당 방법이 선호된다고 합니다. 따라서, 확대된 RoI를 처리하는 것이 적합하다는 것을 의미하게 됩니다. 참고로, egocentric rotation은 3D translation과 카메라의 intrinsic matrix인 K가 주어지면 allocentric rotation에서 쉽게 변환할 수 있다고 합니다.

Parameterization of 3D Translation

이번에는 translation의 parameterization 입니다. 3D 공간에서 이동(translation) t를 직접 regression 하는 것은 실제로 잘 작동하지 않습니다. 이전에 사용되었던 방법론들은 일반적으로 projection된 3D 중심점의 2D 위치 (o_x, o_y)와 카메라를 향한 물체의 거리 t_z로 translation을 분리합니다.

이때 카메라 고윳값 K가 주어지면 back-projection(역투영)을 통해 변환을 식(3)을 통해 계산할 수 있게 됩니다. bounding box 중심 (c_x, c_y)으로 (o_x, o_y)를 approximation 하고 기준이 되는 카메라 거리를 사용하여 t_z를 추정하는 방법도 있고 PoseCNN에서는 (o_x, o_y) 및 t_z를 직접 regression 하는 방법도 있지만, 이러한 방법들은 네트워크가 위치 및 스케일에 대한 invariant parameter를 추정하는 것이 필수적이므로 확대된 RoI를 처리하는 데에는 적합하지 않습니다.

위와 같은 이유로 Scale-Invariant representation for Translation Estimation (SITE) 활용하게 됩니다.

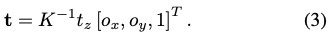
식 (4)을 살펴보겠습니다. detection된 bounding box의 크기 s_o=\max(w,h) 및 중심 (c_x, c_y)과 ratio r=s_{zoom}/s_o가 주어졌을 때, 네트워크에서 scale-invariant translation 파라미터인 T_{SITE}=[\delta_x, \delta_y, \delta_z]^T를 regression 하게 됩니다.

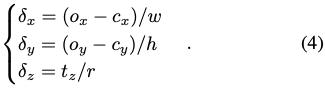
이로써, 3D translation은 식(3)에 따라 얻을 수 있게 됩니다.

Disentangled 6D Pose Loss

회전과 이동의 parameterization외에도 loss function의 선택은 6D Pose estimation 최적화에 매우 중요한 역할을 합니다. 대부분의 연구에서는 angular distance, L_1/L_2 distance와 같이 회전과 이동에 기반한 거리를 직접 활용하는 것 대신에 회전과 이동의 추정을 결합하기 위해 ADD(-S) metric에 기반한 변형된 Point-Matching Loss 를 활용합니다.

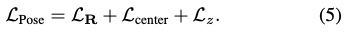
회전 R, scale-invariant 2D 물체의 중심 (\delta_x, \delta_y), 거리 (\delta_z)를 개별적으로 학습하여 변형된 Disentangled 6D pose loss를 적용했다고 합니다.

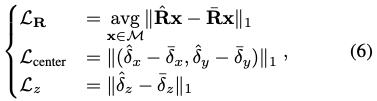
식(5)에 대한 각각의 term은 식(6)을 통해 구할 수 있습니다. \hat \bullet, \bar \bullet은 prediction, GT를 나타냅니다. 여기서 대칭인 물체를 다루기 위해서는 \mathcal L_{R, sym} = \displaystyle \min_{\bar R \in \bar {\mathcal R}} \mathcal L_R(\hat R, \bar R)로 확장할 수 있습니다.

3.2. Geometry-guided Direct Regression Network

논문의 제목인 GDR-Net에 대한 설명을 하는 section입니다. dense correspondence 기반의 기하학적인 특징을 이용하여 6D object pose를 direct regression하는 방법인데요. 따라서, GDR-Net은 dense correspondence 기반한 방법론과 direct regression 방법론을 통합합니다.

Network Architecture

네트워크의 아키텍처를 자세히 살펴보도록 하겠습니다.

처음에는 256 \times 256 크기의 Zoomed-in RoI를 GDR-Net에 입력으로 주고 spatial size가 64 \times 64인 3개의 intermediate geometric feature map을 예측하는데, 이는 dense correspondence map(M_{2D-3D}), Surface Region Attention Map(M_{SRA}), Visible Object Mask (M_{vis})로 구성됩니다.

본질적으로는 M_{XYZ}와 M_{vis} regression을 위한 layer들은 유지하면서 disentangled translation head는 제거하는 과정을 거친다고 합니다. 추가적으로 저자는 M_{SRA}에서 필요로 하는 채널을 ouput layer에 추가했다고 합니다. 이러한 intermediate geometric feature map은 모두 이미지에 대해 2D-3D correspondence로 구성되어 있기 때문에 간단하면서도 효과적인 convolutional-PnP 모듈을 사용하여 M_{2D-3D} 및 M_{SRA}으로부터 물체에 대한 6D pose를 direct regression합니다.

Dense Correspondences Maps (M_{2D-3D})

앞서 언급된 M_{2D-3D}인을 dense correspondences map을 계산하기 위해서는 먼저 dence coordinate map (M_{XYZ})을 추정해야 합니다. 그런 다음 해당 2D 픽셀 좌표에 M_{XYZ}를 stack하면 M_{2D-3D}를 얻을 수 있습니다. 특히 물체의 CAD 모델이 주어지면, 연관된 pose가 주어진 모델에서 물체의 3D 좌표를 렌더링하여 M_{XYZ}를 얻을 수 있게됩니다. 여기서 추가적으로 네트워크에서는 M_{XYZ}의 normalization된 representation을 예측하도록 합니다. M_{XYZ}의 각 채널은 CAD 모델에 해당하는 tight한 3D bounding box 크기인 (l_x, l_y, l_z)로 [0, 1] 내에서 normalization 됩니다.

Surface Region Attention Maps (M_{SRA})

기본적으로 M_{SRA}의 GT region은 가장 멀리 있는 지점에 대한 샘플링을 사용하는 M_{XYZ}으로 부터 얻을 수 있습니다. 각 픽셀에 대해 해당 영역을 분류하므로 예측된 M_{SRA}의 확률은 물체의 대칭성을 내포하고 있습니다. 예를 들어 대칭으로 인해 2개의 가능한 부분에 픽셀이 할당된 경우, 해당 할당을 최소화하려면 각 픽셀에 대해 0.5의 확률이 반환됩니다. 또한 M_{SRA}를 활용하면 모호성의 영향을 완화하면서 M_{3D}를 보조하는 역할로도 활용할 수 있습니다. 즉, 먼저 coarse한 영역을 찾은 다음에 더 세밀한 좌표를 regression하여 M_{3D}학습을 용이하게 할 수 있습니다. patch-PnP의 symmetry-aware attention로 가이드 하기 위해 M_{SRA}를 활용한다고 한다고 볼 수 있습니다.

Geometry-guided 6D Object Pose Regression

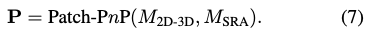
이미지 기반 기하학적 feature patch (M_{2D-3D}, M_{SRA})들을 사용하여 물체의 direct 6D pose regression을 위한 Patch-PnP를 식(7)로 나타낼 수 있습니다.

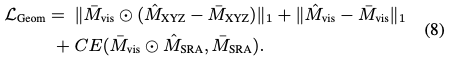
정규화된 M_{XYZ}, visible mask M_{vis}에는 L_1 loss, M_{SRA}에는 Cross entropy를 사용하여 최종 gemetry-guided loss인 식(8)을 나타냅니다. 즉, 전체적인 loss를 요약하면 \mathcal L_{GDR}= \mathcal L_{Pose} + L_{Geom}으로 나타낼 수 있습니다.

Decoupling Detection and 6D Object Pose Estimation

저자는 물체의 네트워크가 6D pose estimation과 2D detector를 이용하여 Zoom-in 된 RoI를 얻는 것에 초점을 맞추었다고 합니다. 해당 과정은 정확도를 향상시킬 수 있는 장점가지게 됩니다. 이전에 제가 CDPN 리뷰에서 사용하였던 Dynamic Zoom-in(DZI)를 단순화시켜 GDR-Net과 object detector와 분리를 하여 학습할 수 있도록 하는 역할을 하도록 적용했다고 합니다. 학습 동안 center에 대한 좌표를 uniformly shift를 해주는 작업과 GT의 bounding box 비율을 25%로 조정을 하는 작업을 했다고 합니다. 그 다음 원래의 aspect ratio를 유지하면서 r=1.5 비율로 입력에 대한 RoI를 확대합니다. 이렇게 할 경우 물체가 포함된 영역이 RoI의 약 절반정도가 됩니다. 또, DZI는 scale에 대한 고려를 할 필요가 없게 되는 장점이 생기게 됩니다.

4. Experiments

Patch PnP의 성능 향상에 대한 증명을 실험을 통해서 하는 섹션입니다. 이러한 성능 향상을 Toy experiment로 Synthetic Sphere 진행하고 Ablation Study로 LINEMOD(LM)에서 진행합니다. 챌린지 데이터셋인 LM-O(Occlusion), YCB-V에 대해서 성능 비교를 하여 SOTA를 달성했다고 합니다.

4.1. Experimental Setup

Datasets

Synthetic Sphere 데이터셋에도 진행을 했는데, 생소해서 정리를 했습니다. 해당 데이터셋은 focal lenth가 800, 640 \times 480의 해상도, 이미지 중심에 위치한 principal point를 사용하여 calibration이 적용된 virtual camera를 사용하여 unit sphere model(단위 구 모델)을 random하게 캡쳐하여 만든 train sample이 2만개, test sample이 2천개로 구성되어있다고 합니다. rotation, translation은 3차원 공간에서 각각 일정 간격 내에서 균일하게 샘플링이 된다고 합니다.

4.2. Toy Experiment on Synthetic Sphere

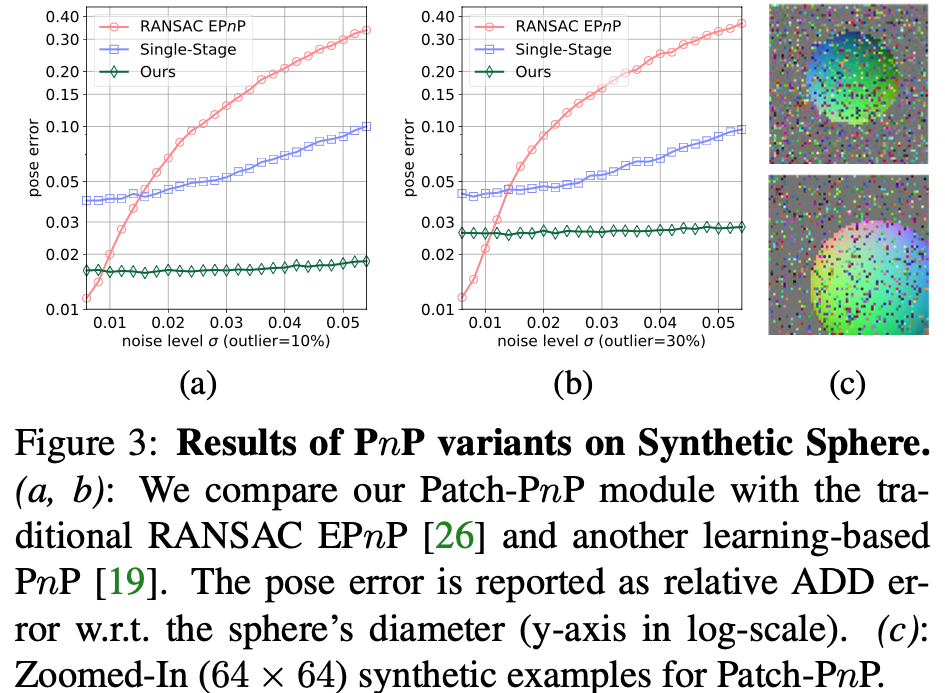
Synthetic Sphere 데이터셋으로 Patch-PnP와 RANSAC EPnP를 서로 비교하는 실험입니다. 제공되는 pose 정보로부터 M_{XYZ} 를 생성하여 Patch-PnP에 입력으로 합니다. 이때 공정한 비교를 위해 M_{SRA}는 입력에서 제외를 했다고 합니다. 학습 중에 dense coordinate map의 각 지점에 대해 무작위로 Gaussian noise를 주었습니다. 이렇게 noise를 주면 coordinate map이 [0, 1]로 정규화가 되고 M_{XYZ}에 대해 이상치를 무작위로 0~30%를 준 모습이 그림3(c)입니다. 테스트 과정은 다양한 noise와 이상치를 가진 테스트셋에 대해 구의 diameter에 따른 상대적인 ADD error를 리포팅 한 결과입니다.

Comparison with PnP/RANSAC and [19].

[19] Yinlin Hu, Pascal Fua, Wei Wang, and Mathieu Salzmann. Single-Stage 6D Object Pose Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2930–2939, 2020.

그림3에서는 patch-PnP를 기존의 RANSAC-based EPnP 및 1-stage 모델인 learning-based PnP와 비교하여 이번 논문에서 제안한 접근 방식의 효과와 robust함을 입증하게 됩니다. 그림3에서 볼 수 있듯이, noise가 많이 적을 때는 RANSAC-based EPnP가 더 정확하지만 이는 비현실적으로 noise가 적은 상황이고 실제 현실에서는 noise가 많으므로 noise-level이 높아질수록 learning-based PnP가 더 정확하고 robust합니다. 하지만 Patch-PnP는 기하학적인 정보를 훨씬 더 풍부하게 가지고 있고 Dense correspondence map을 이용하기 때문에 noise와 이상치에 대해 학습 기반 방법론 보다 좀 더 robust한 모습을 볼 수 있습니다.

4.3. Ablation Study on LM

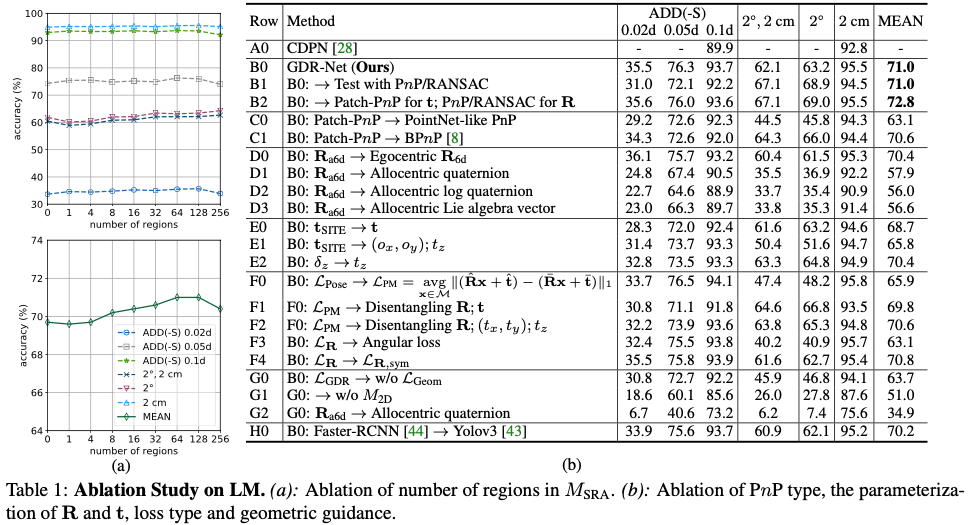
전체적인 정확도가 region이 증가할수록 높아지지만 64부터는 줄어드는 것을 볼 수 있습니다. 해당 결과를 통해 64개의 region을 사용하여 정확도와 메모리에 대한 trade-off에 대해서 적절하게 고려할 수 있도록 설정하였다고 합니다. 그리고 각 방법론에 대해 해당 논문에서 제안된 방법론들을 적용했을 때에 대한 결과에 대한 정량적 평가를 표1(b)에 리포팅 된 것을 볼 수 있습니다.

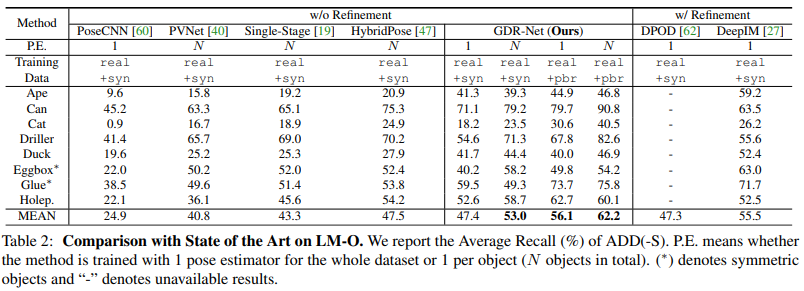
4.4. Comparison with State of the Art

5. Conclusion

이번 논문에서는 Direct 6D pose regression의 구성 요소를 다시 재검토하여 direct method와 geometry-based indirect method을 통합하는 GDR-Net을 제안하였습니다. 여기서 핵심은 이미지와 같은 2D patch로 규칙적으로 구성된 2D-3D correspondence에 대한 intermediate geometric 특징을 활용하여 간단하면서도 효과적인 2D convolutional patch-PnP를 사용하여 geometric guidance에서 6D pose를 direct regression 하는 것입니다.

---

마지막으로 저자는 detector 파트에 YOLOv3를 사용하여 한 물체에 대해 약 22ms, 8개 물체에 대해 35ms 정도가 걸렸다 정도만 짧게 끝내는데, 해당 real-time 속도적인 부분에 대한 리포팅은 supplementary에도 있으면 좋을 것 같다고 생각이 들어 찾아봤지만 관련된 ablation study가 없어 아쉬운 논문인 것 같습니다.