Before Review
이번 리뷰는 당장 저의 연구와는 큰 관련이 없을 수 있지만 예전부터 공부해 보고 싶었던 GNN에 대해서 다뤄보았습니다.
Graph Neural Network가 Computer Vision Domain에서는 많이 사용이 되고 있지는 않지만(주로 추천 시스템) 그럼에도 GNN과 Vision Data를 결합한 연구들을 볼 수 있습니다. 가끔은 정말 필요한 연구임에도 불구하고 GNN을 사용했다는 이유만으로 논문 공부를 피하는 경우가 있었습니다. 더불어 제가 알기로는 저희 연구실에서도 GNN을 공부해본 사람이 거의 없는 것으로 알고 있습니다.
이번 리뷰를 통해 저 뿐만 아니라 RCV 연구원들에게 GNN은 더 이상 피해야할 대상이 아니라, Convolution, Transformer와 같이 필요할 때 언제든지 활용할 수 있는 하나의 도구가 되길 희망하면서 글을 작성합니다.
하나의 리뷰로 다 작성해보려고 하다가 분량이 너무 많은 관계로 2부로 나누어서 작성하겠습니다.
Introduction
지난 10년간 Neural Network는 computational resources (eg.. GPU), big training data 그리고 deep learning의 latent representation 덕분에 다양한 패턴인식, 데이터 마이닝 분야에서 탁월한 성공을 거두었습니다.
Neural Network 성공 이전에는 Handcrafted Feature에 의존했었지만 end-to-end deep learning 패러다임 (eg.. CNN, RNN, Autoencoder)이 등장하면서 Object Detection, Speech Recognition, Machine Translation 등과 같은 작업의 정확도는 매우 빠른 속도로 높아지고 있습니다.
Convolution의 경우 이미지 데이터를 분석하는데 있어 local connectivity, shift invariance 등을 고려하기 매우 적합한 구조라 image data의 구조를 파악하는데 아주 적합합니다. 사실 여기까지는 Computer Vision 연구자로써 당연히 알고 있는 이미지 데이터의 특징입니다. 하지만 한가지 더 고려해야 할 것은 이미지 데이터는 바로 Euclidean Data라는 것 입니다.
Euclidean data’ is data which is sensibly modelled as being plotted in ?-dimensional linear space, for example image files (where the ? and ? coordinates refer to the location of each pixel, and the ? coordinate refers to its colour/intensity).
즉, Euclidean Data는 유클리드 공간에서 표현할 수 있는 모든 데이터를 의미합니다. 이미지 데이터 역시 3차원 공간에서 모두 표현이 가능합니다. X축은 가로, Y축은 세로, Z축은 픽셀의 명도값에 대응을 시킨 다음에 이미지에 대응되는 모든 점들의 집합을 고려하면 하나의 이미지 데이터를 표현할 수 있겠네요. (물론 R,G,B를 모두 고려하기 위해서는 4차원 공간이 필요할 듯 합니다.)
그런데 이러한 Euclidean Data의 특징은 statistical properties를 가진다는 것 입니다.
이미지 데이터의 경우 고양이 사진이 있을 때 고양이의 위치가 shift 되어도 크게 상관이 없습니다. 즉, shift invariance라는 소리인데, 이는 고양이의 위치 주변이 어떤 픽셀 패턴으로 구성이 되어있는지가 더 중요하다는 소리 입니다.
또한 compositionality through local statistics라는 얘기도 있는데 이는 local feature를 구성하는 과정에서 점이 모여 선, 선이 모여 곡선, 이런식으로 모여서 눈,코,입,귀 등 특징을 이루는 식으로 이해하면 됩니다.
기존의 딥러닝 framework는 이러한 Euclidean Data의 statistical properties를 굉장히 잘 활용하여 성공을 거두었습니다. 사실 위에서 설명하는 성질들은 이미 convolution 연산이 잘 고려하여 수행을 하고 있습니다.
기존의 딥러닝 연구들은 이렇게 Euclidean Data에 대해서는 데이터의 숨겨진 패턴을 잘 찾을 수 있지만 Non-Euclidean Data에 대해서는 연구가 부족한 상황입니다. Non-Euclidean Data는 어떤게 있을까요? 쉽게 말하면 유클리드 공간에서 표현할 수 없는 모든 데이터를 의미하지만 결국 그래프 데이터를 얘기하기 위해 이렇게 길게 돌아왔습니다.

지금부터 중점적으로 얘기할 그래프 데이터는 유클리디언 공간에 표현하기 어렵습니다. 선형적인 구조가 아니라 굉장히 복잡한 비선형적 구조이며 노드간의 방향, 간선 간의 가중치 등 이런것들을 고려해보면 유클리디언 공간에 그대로 표현할 수 없습니다.
Graph Neural Network는 결국 이러한 Non-Euclidean Data인 그래프를 신경망을 이용하여 해석하고 다양한 task로 확장할 수 있게 하기 위한 연구라고 보시면 됩니다. Graph Neural Network에 대한 본격적인 얘기는 뒤에서 할 예정인데 간단하게 Graph Convolution에 대해서만 살짝 얘기하고 이제 intro를 마치도록 하겠습니다.
Graph Convolution은 일반화된 Convolution의 형태라고 보시면 됩니다.
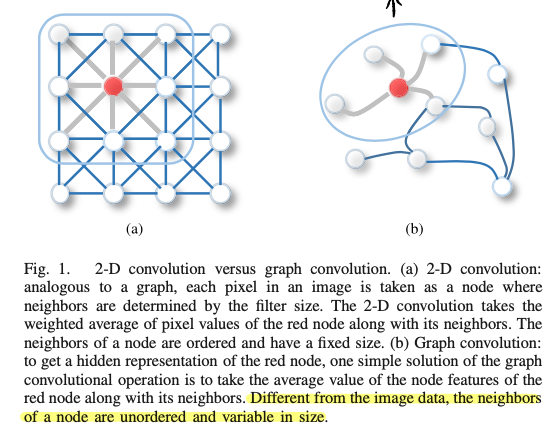
이미지 데이터를 처리할 때 픽셀 하나를 하나의 노드라고 가정한다면, 노드의 이웃들은 convolution filter의 kernel size에 의해서 정해지게 됩니다. 이러한 관점에서 기존의 convolution은 이웃의 갯수가 고정적이고 순서가 존재하게 됩니다. 이에 반해 그래프 데이터를 처리할 때 기존의 2D convolution과 다른 점은 이웃의 갯수가 노드마다 다르고 순서가 존재하지 않는다는 것 입니다.
이렇게 Graph Neural Network는 그래프라는 Non-Euclidean Data를 처리 하기 위해서 기존의 CNN이나 RNN과 같은 딥러닝 연구의 기본적인 구조는 비슷하게 가져가지만 그래프라는 데이터의 구조를 좀 더 잘 처리하기 위해 연구가 되고 있습니다.
그럼 이제 GNN에 대해서 하나씩 차근 차근 알아가보도록 하겠습니다.
Background and Definition
Background
Brief History of Graph Neural Network
처음으로 neural network를 이용하여 그래프를 해석하려고 했던 시도는 1997년에 있었습니다. 유향 비순환 그래프(Directed Acyclic Graph)에 적용이 되었는데 그 이후로 점점 정교해지고 발전하면서 초기에 GNN 연구들은 Recurrent GNN에 초점이 맞춰져 있었습니다. 연구의 핵심은 target node의 representation을 이웃 node의 정보를 반복적으로 propagation 시키면서 안정적인 fixed node가 될 때까지 하는 것이였습니다. 하지만 초기의 이러한 연구들은 계산복잡도가 높아 이러한 한계점들이 존재했죠.
Computer Vision 도메인에서 CNN의 성공 덕분에, 많은 연구들에서 CNN의 방법을 토대로 그래프 데이터를 해석하려는 시도가 있었습니다. ConvCNN 인데 여기서 두 가지의 흐름으로 나뉜다고 합니다. 여기서 spectral graph 이론(Spectral graph theory는 Laplacian matrix과 관련된 행렬의 특성 다항식, 고유값, 고유 벡터와 관련된 그래프 속성에 대한 연구)에 기반하여 시작된 spectral-based ConvGNN이 있고, 이보다 더 일찍 연구가 시작된 spatial-based ConvGNN이 있습니다.
Graph Neural Network Versus Network Embedding
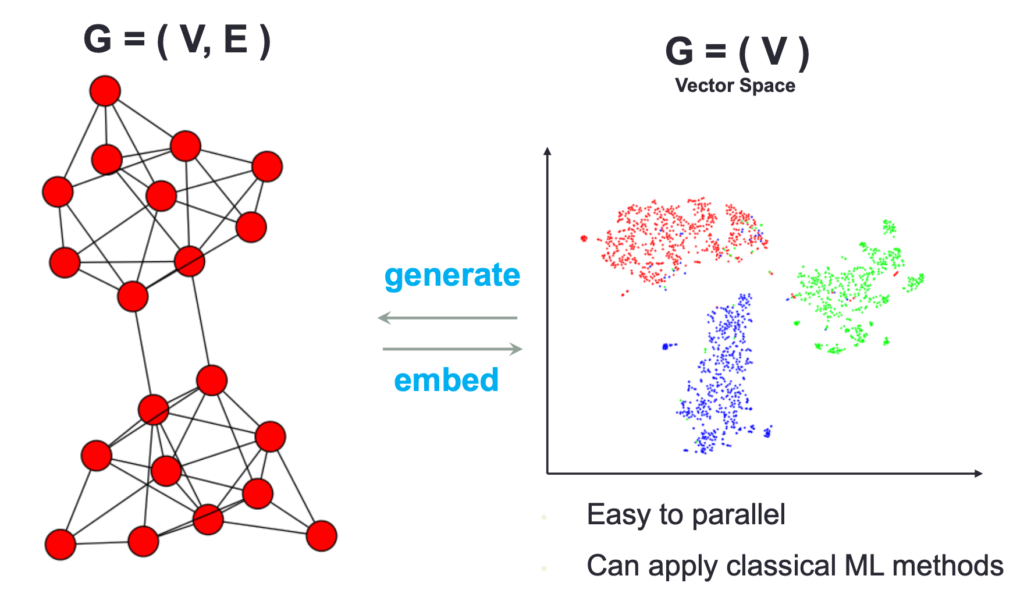
Network embedding이란 network 노드들을 low-dimensional 벡터로 표현하는 것을 의미합니다. 이 때 중요한 것은 network의 위상구조적 정보와 노드들의 콘텐츠 정보를 잘 유지하는 것 입니다. 이러한 network embedding representation을 가지고 classification이나 clustering 그리고 recommendation 들을 수행하게 됩니다. GNN은 이러한 network embedding을 end-to-end 방식으로 가능하게 합니다. 기존 network embedding 방식 보다 더욱 포텐셜이 높다고 볼 수 있습니다.
Graph Neural Network Versus Graph Kernel Methods
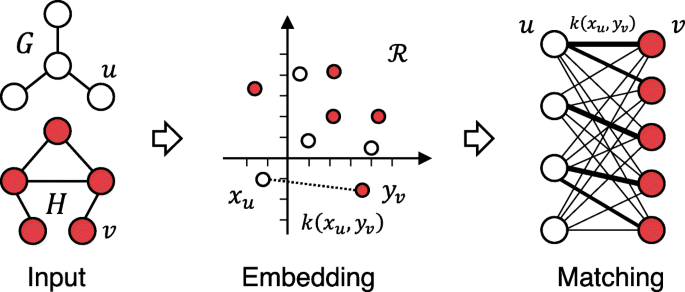
Graph kernel은 전통적으로 graph classification 문제를 풀 때 사용하는 가장 흔한 방법이었습니다. 이러한 방식은 SVM에서 사용되는 kernel method와 비슷하게 kernel function을 사용하여 graph pair간의 유사도를 측정하고 지도학습 기반으로 머신러닝 분류 작업을 하는 것 입니다.
GNN은 이러한 kernel function의 역할을 하기도 합니다. 기존의 kernel function은 deterministic하다고 볼 수 있습니다. 하지만 GNN을 이용하면 더욱 높은 포텐셜을 가질 수 있는 학습 기반의 kernel function을 얻을 수 있습니다. 자세한 내용은 나와있지 않지만 전통적인 kernel method를 사용하면 계산 복잡도가 너무 높아서 문제였는데 GNN을 이용하면 이러한 문제를 해결할 수 있다고 하네요.
기존의 그래프 데이터를 해석할 때 사용하는 전통적인 방식과 GNN과의 차이점을 간단하게 설명해드렸습니다. 복잡한 얘기는 됐고 그냥 GNN을 사용하면 더욱 다양하고 풍부한 representation을 얻을 수 있음과 동시에 연산량 측면에서도 기존의 방법보다 더욱 효율적이라고 하네요.
Definition
뒤에 내용을 얘기하다 보면 수식이 많이 나오는데 이를 위해 간단하게 notation에 대해서 정리하도록 하겠습니다.
Definition 1. Graph

그래프는 G=(V,E) 이렇게 표현 합니다. 이 때 V는 node 혹은 vertex의 집합이라 보시면 됩니다. E는 node와 node를 연결해주는 edge들의 집합입니다.
- v_{i} \in V를 node라 정의하고, e_{ij}=\left( v_{i},v_{j}\right)를 node v_{i}에서 v_{j}로 향하는 edge라 정의하겠습니다.
- node v의 이웃은 N(v)=\left\{ u\in V\mid (v,u)\in E\right\} 로 v와 edge로 연결되어 있는 node들의 집합으로 정의 됩니다.
- 인접행렬(adjacency matrix) A는 n \times n 행렬로 A_{ij}=1 if e_{ij}\in E and A_{ij}=0 if e_{ij}\notin E node 들끼리 edge로 연결되면 성분이 1 아니면 0의 값을 가지도록 정의 됩니다.
아마 위의 내용까지는 보통의 알고리즘 수업때 배우는 내용이기 때문에 이해하는데 크게 어려움은 없을 것 같습니다. 여기서 추가적으로 알아야하는 부분은 node나 edge를 표현하는 feature 들이 정의된다는 것 입니다.
- X^{v}\in R^{n \times d}은 node feature matrix로 x_{v} \in R^{d}로 node v를 표현하는 하나의 feature vector 입니다.
- X^{e}\in R^{m \times c}은 edge feature matrix로 x^{e}_{v,u} \in R^{c}로 edge (u,v)를 표현하는 하나의 feature vector 입니다.
Definition 2. Directed Graph

방향 그래프는 node들끼리 edge로 연결이 되어 있어도 그 방향을 고려하는 그래프를 의미합니다. 무방향 그래프는 node들끼리 연결되어 있기만 한다면 방향은 고려하지 않는 그래프를 의미합니다. 무방향 그래프를 따로 신경쓸 필요는 없고 결국 인접행렬이 대칭행렬이라면 무방향그래프라 이해하면 되고 그렇지 않다면 모두 방향 그래프 입니다.
Definition 3. Spatial-Temporal Graph
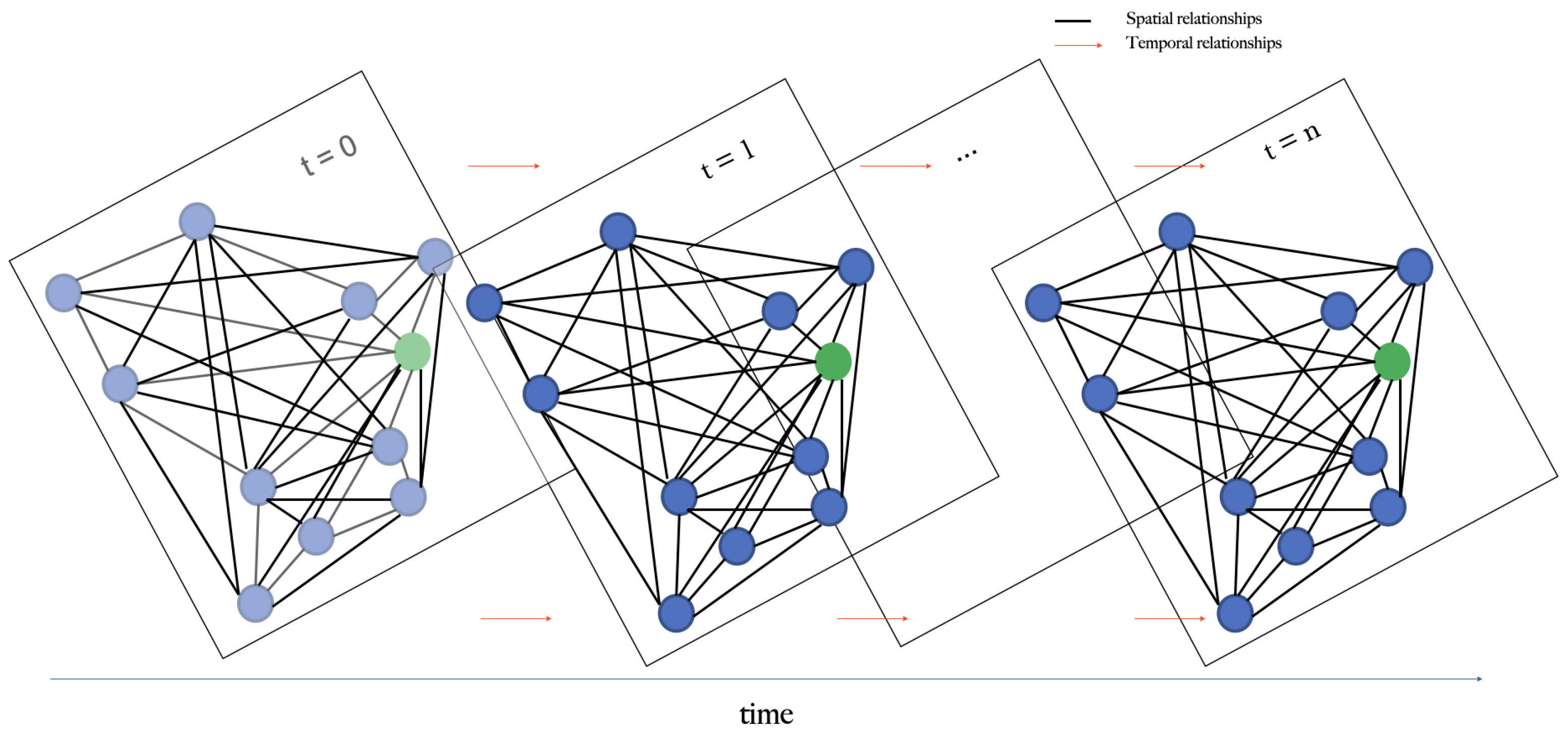
Spatial Temporal Graph는 시간에 따라 그래프가 dynamic하게 변화하는 데이터 구조를 의미합니다.
- G^{(t)}=(V,E,X^{(t)}) , X^{(t)}\in R^{n \times d}
예를 들면 비디오 데이터의 Scene Graph 변화 혹은 날짜별 사용자의 SNS 네트워킹 변화 등이 해당될 것 같습니다.
Categorization and Frameworks
Taxonomy of Graph Neural Networks
Recurrent Graph Neural Networks
Recurrent Graph Neural Networks(이하 RecGNN)은 가장 초기 GNN 연구에 해당 됩니다. 말 그대로 recurrent neural network 구조를 활용해서 node representation을 학습 합니다.
뒤에서 더 자세히 알아보겠지만, hidden state를 가지고 information을 propagation 하는 방식으로 진행이 됩니다. 즉, node 간의 이러한 information/message 교환이 이루어지면서 사전에 정의한 수렴 조건을 만족 시킬 때 readout layer로 마지막 state를 전달해주게 됩니다.
이러한 message passing 방식의 아이디어는 spatial-based ConvGNN의 근간이 되기도 합니다. 굉장히 축약
Part.2에서 Recurrent Graph Neural Network를 다룰 때 더 자세히 설명하도록 하겠습니다.
Convolutional Graph Neural Networks
Convolutional Graph Neural Network(이하 ConvGNN)는 기존 이미지 데이터(Grid Data)에서 사용하는 Convolution을 그래프 데이터 에서도 활용할 수 있도록 Convolution 연산을 Generalization 시킨 신경망 방법론 입니다.
기본적인 아이디어는 node v의 representation x_{v}을 주변 이웃 노드들 u \in N(v) 의 representation x_{u}와 weighted aggregating을 통해서 생성하는 것 입니다.
RecGNN은 동일한 weight layer를 공유하는 반면에 ConvGNN은 multiple layer를 사용한다는 것이 주된 차이 입니다.
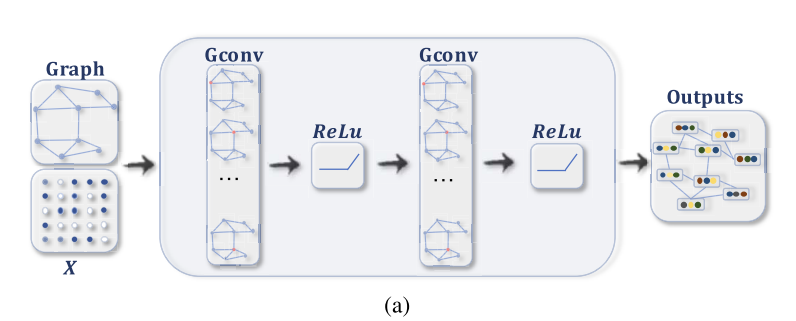
위의 그림은 node classification 과정을 담고 있는 흐름도 입니다.
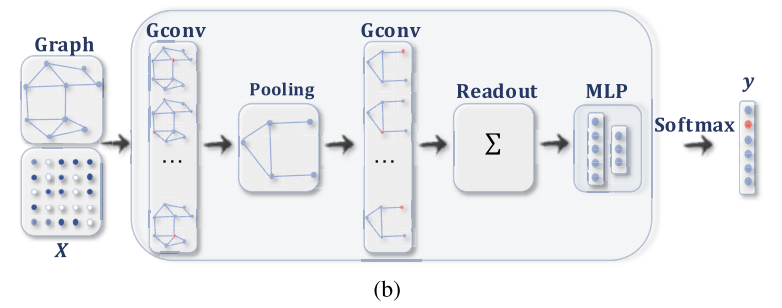
위의 그림은 graph classification 과정을 담고 있는 흐름도 입니다.
Graph Convolution에 대한 forward 과정은 뒤에서 좀 더 자세히 설명하고 결국에는 저희가 CNN에서도 하는 것과 비슷하게 multiple ConvGNN을 거쳐서 나온 output을 토대로 downstream task를 수행하게 됩니다.
Graph Autoencoders
Graph Autoencoder(이하 GAE)는 보통 비지도학습 상황에서 사용되며, node나 grpah를 latent vector space로 embedding 시킬 때 사용합니다. 여기서 embedding 시킨 vector를 가지고 다시 graph나 node를 reconstruction 하는 과정을 통해 진행이 됩니다. 즉, graph generative distribution을 통해서 GAE가 학습이 된다고 보시면 됩니다.
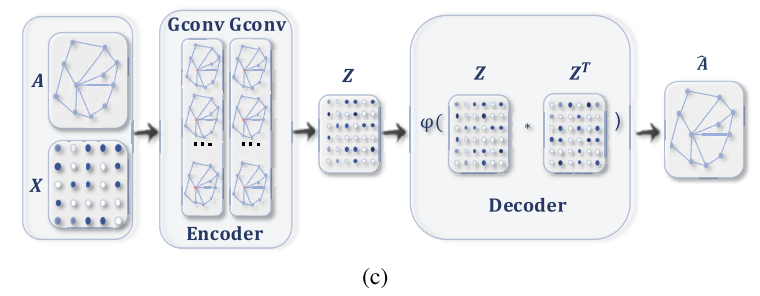
결국에는 graph의 인접 행렬을 정교하게 다시 잘 복원하는 것이 중요하다고 볼 수 있습니다. 방법론에 따라서 node나 edge를 순차적으로 복원하는 방법도 있고, 아니면 그래프 자체를 한번에 복원하는 방법도 있습니다.
Spatial-Temporal Graph Neural Networks
이름에서 바로 알 수 있지만, 위에서 정의 했던 spatial-temporal graph의 숨겨진 패턴을 찾기 위해 학습한다고 보시면 됩니다. 아무래도 정적인 그래프를 해석하는 것보다는 시간 흐름에 따라 그래프의 변화를 찾는 작업이 더욱 중요해지고 있기 때문에 최근에 많은 관심을 받고 있는 연구 분야라고 보시면 됩니다.
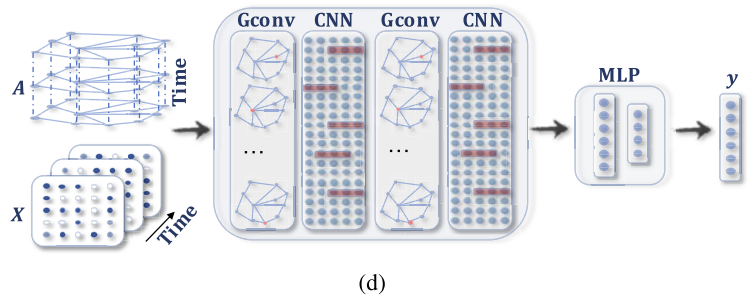
핵심 아이디어는 spatial dependency와 temporal dependency를 한번에 고려하는 것 입니다.
본 논문 기준으로는(20년도 기준) 당시 연구의 흐름은 graph convolution을 통해 spatial dependency를 modeling 하고 RNNs 혹은 CNNs를 활용하여 temporal dependency를 modeling 했다고 합니다.
Frameworks
그래프 데이터 자체의 특성에 맞춰서 GNN의 출력에 따른 framework를 구분할 수 있습니다. 아래에서 간단하게 설명하도록 하겠습니다. 간단히 말하면 node , edge , graph 중 어떤 것에 집중을 할 것 인지에 따라 나뉜다고 보시면 됩니다.
Node Level
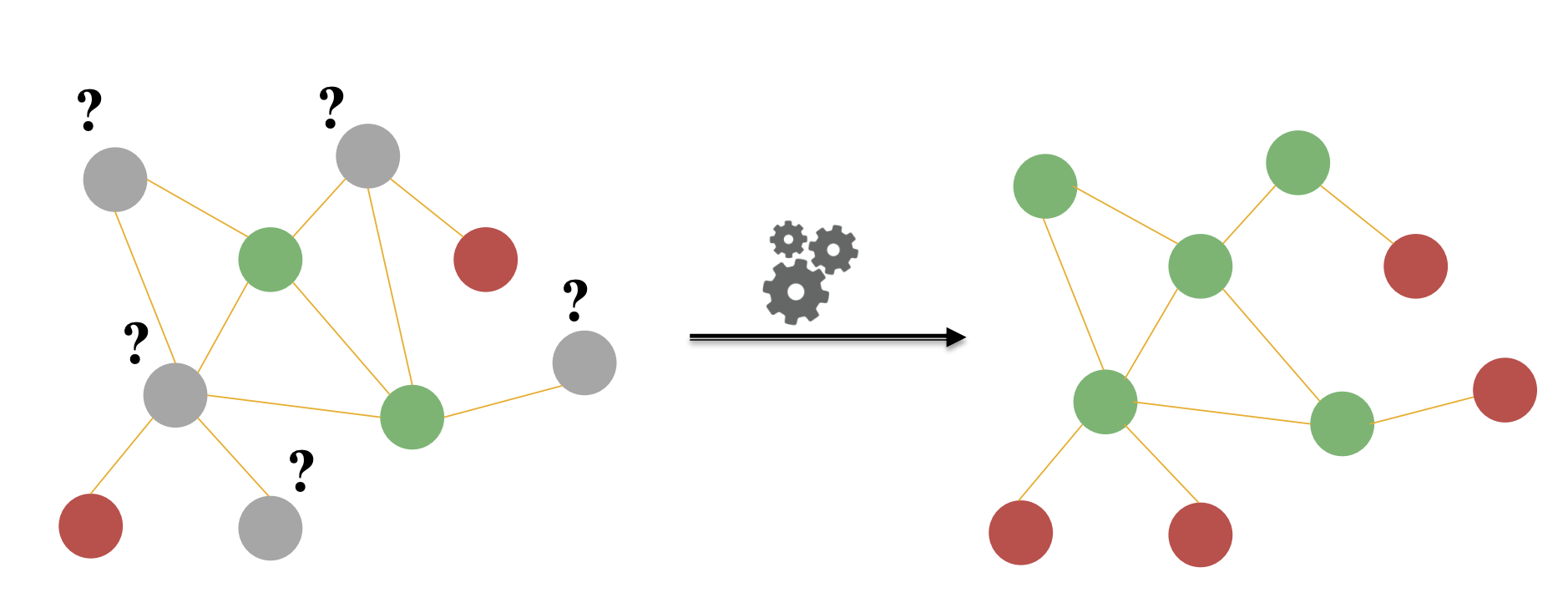
GNN의 출력 값이 node regression 혹은 node classification에 집중하게 됩니다. 위에서 설명한 RecGNN 혹은 ConvGNN의 구조를 활용하여 information propagation / graph convolution을 통해 high-level node representation을 얻고 MLP를 통해서 regression 혹은 classification 문제를 풀게 됩니다. 이러한 node-level task를 GNN은 end-to-end 방식으로 학습할 수 있게 되는 것입니다.
Edge Level
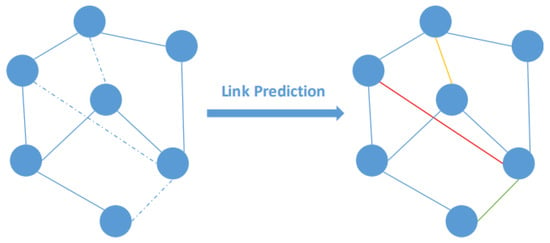
GNN의 출력 값이 edge classification 혹은 link prediction에 집중하게 됩니다. 서로 다른 두개의 노드에 대해서 GNN을 통해 hidden representation을 얻고 similarity function 혹은 neural network를 통해 노드간 유사도를 계산하게 됩니다. 이를 가지고 edge 단위의 label 혹은 connection 관계를 modeling 하게 되는 것이죠.
Graph Level

GNN의 출력 값이 graph classification에 집중하게 됩니다. node 그리고 edge 단위의 representation을 pooling 하고 readout 하여 graph 단위의 compact 한 representation을 얻고 이를 토대로 classification 작업을 수행합니다. Pooling이나 Readout 연산에 대한 디테일은 2부에서 다루도록 하겠습니다.
첫번째 질문으로 리뷰 내용 중 “이미지 데이터를 처리할 때 픽셀 하나를 하나의 노드라고 가정한다면, 노드의 이웃들은 convolution filter의 kernel size에 의해서 정해지게 됩니다. 이러한 관점에서 기존의 convolution은 이웃의 갯수가 고정적이고 순서가 존재하게 됩니다. 이에 반해 그래프 데이터를 처리할 때 기존의 2D convolution과 다른 점은 이웃의 갯수가 노드마다 다르고 순서가 존재하지 않는다는 것 입니다.” 부분에서 컨볼루션은 순서가 존재한 반면에 그래프 데이터는 순서가 존재하지 않는다라고 하셨는데, 이 순서에 대해서 조금 더 자세한 설명해줄 수 있으신가요? 컨볼루션에서 각 픽셀간에 순서라 함은 spatial 위치 좌표를 의미하는건가요? 그럼 그래프 데이터에서는 부모노드 자식노드와 같은 느낌으로 순서를 나타낼 수는 없는 건가요?
아니면 순서에 대해서 제가 잘못 이해를 한 것인지요?
그리고 둘째로 리뷰 내용 중 ” 복잡한 얘기는 됐고 그냥 GNN을 사용하면 더욱 다양하고 풍부한 representation을 얻을 수 있음과 동시에 연산량 측면에서도 기존의 방법보다 더욱 효율적이라고 하네요.” 있다고 하셨는데, 이는 전통적인 기법과 비교하였을 때 GNN이 빠르다는 점을 말씀하신 것이지요? 그럼 실제로 CNN 혹은 RNN 등과의 대략적인 비교를 통했을 때 GNN은 빠른 편에 속하는지도 알려주실 수 있나요?
마지막으로, “이미지 데이터의 경우 고양이 사진이 있을 때 고양이의 위치가 shift 되어도 크게 상관이 없습니다. 즉, shift invariance라는 소리인데, 이는 강아지의 위치 주변이 어떤 픽셀 패턴으로 구성이 되어있는지가 더 중요하다는 소리 입니다.” 이미지 데이터는 고양이인데 뒷 문장은 강아지라고 작성하셨네요 수정 부탁드립니다.
첫번째 질문에 답변을 드리자면 이미지는 픽셀들의 절대적인 위치 좌표가 존재하기 때문에 순서를 고려할 필요가 없습니다. 하지만 그래프 데이터는 노드들의 index numbering이 달라지면 인접행렬이 달라지고 이러한 permutation invariance 문제가 발생해서 저렇게 서술했습니다.
두번째 질문에 답변을 드리자면 연산량이 줄어든다는 것이 CNN이나 RNN에 대해서 직접적인 비교를 했던 것이 아니라 Graph Kernel Method와 비교를 했던 것 입니다. GNN의 구조 자체는 CNN이나 RNN과 다를게 거의 없어서 특별히 구조적으로 연산이 빠른 부분이 없습니다. 그 부분은 데이터의 볼륨에 따라 다르겠네요.
강아지는 수정하였습니다 감사합니다.
좋은 리뷰 감사합니다.
node classification과 graph classification을 다룬 그림에 대해 간단한 질문이 있습니다.
(a)같은 경우, MLP에 activation function 사용하여 output을 뽑고 (b)는 convolution 연산을 하는 것처럼 보이는데 기본적인 프레임워크의 틀은 MLP나 CNN과 별로 다름이 없어보이는데, spatial한 부분과 temporal한 부분을 동시에 고려할 수 있다는 것이 CNN과 큰 차이점으로 이해하면 될까요?
감사합니다.
temporal한 부분을 고려하는 것은 Spatial-Temporal GNN 밖에 없는데 그 부분을 조금 헷갈리신 것 같습니다.
GNN 같은 경우도 역시 전체적인 구조가 Graph Conv + Activation + Graph Conv + Activation 이런식으로 CNN과 비슷합니다. 결국 가장 다른 점은 Graph Convolution의 forward 방식이 다르다고 볼 수 있겠네요. 이 부분은 어제 세미나에서 자세하게 설명했으니 아마 이해하셨을거라 생각이 듭니다.
안녕하세요. 임근택 연구원님.
좋은 리뷰 감사합니다.
저도 GNN이 필요하다고 느끼면서도 가끔 마주치면 도망가기 바빴는데, 덕분에 드디어 GNN을 조금이나마 알게 되었습니다.
리뷰를 읽고 몇 가지 궁굼한 점이 생겼는데요.
1. Network Embedding을 통해 그래프가 low-dimensional vector로 변환이 된다는 것은 그래프를 Euclidean data로 변환한다는 것으로 봐도 될까요?
2. Spatio-Temporal GNN 그림에서 Gconv -> CNN 다음 다시 Gconv가 나오는 식으로 그림이 되어 있는데, Gconv를 거치고 CNN을 거친 feature를 다시 Gconv에 넣는 것인가요?
본 리뷰를 통해 GNN에 대한 두려움이 많이 걷힌 것 같습니다. 2편이 기대됩니다. ?
감사합니다!
1. 네 맞습니다.
2. 1D conv를 통과한 feature matrix가 다시 GConv Layer에 들어간다고 보시면 됩니다.
안녕하세요 임근택 연구원님. 리뷰 잘 읽었습니다.
항상 궁금했는데요. GNN에서는 그럼 노드는 픽셀이니까 내버려두고, 간선을 convolution의 weight와 bias의 개념으로 보고 최적화를 수행하나요?
어제 세미나에서 답변을 드린 것 같네여. 픽셀 단위에서는 GNN을 잘 적용하지는 않고 instance 단위에 대한 feature를 node로 보통 정의하고 사용합니다.
안녕하세요. 리뷰 흥미롭게 읽었습니다.
수월히 작성되어 있어도 GNN을 이해하는 것은 쉽지 않네요.
우선 Network embedding을 통해 Graph를 Vector space로 보내는 이유는 이해되지만 결국 Vector space에서 어떻게 Node 간의 Weight (content) 정보를 유지할 수 있을지 궁금합니다. Edge (위상구조) 정보는 머리 속으로 떠오르지만, 복잡한 구조를 보일 때 Vector space 내 모든 Node Vetor들이 서로 간의 Weight를 표현하기란 수학적으로 쉽지 않을 것으로 보여 궁금합니다.
두 번째 Graph Kernel Method와 비교하여 말씀해주셨는데, Graph Kernel Method 또한 Vector space로 embedding한 다음 Support vector와 같은 Kernel을 통해 분류 등의 작업을 수행하는 것인가요? Graph Kernel Method에 대한 보충적인 설명을 해주시면 감사합니다.
마지막으로 GNN에 대한 일반적인 질문으로, GNN에서 회귀, 분류등의 태스크를 진행한다고 하셨는데 만약 일방향 그래프라면 최종 노드를 통해 분류를 진행하나요? 그렇다면 무방향 그래프라면, 혹은 가중치 그래프 등의 다양한 상황에서는 노드들을 모두 조합하여 분류를 진행하는지 등의 다양한 그래프에 대해 태스크를 진행할 때 노드, 간선, 가중치 들의 역할이 궁금합니다.
Part. 2가 기대되는 리뷰네요. GNN에 대해 흘낏 살펴보고자 했는데 감사합니다.
1. 그래프의 구조를 보존하기 위해 Graph Convolution이 제안되었습니다. 이는 세미나에서 자세히 다뤘긴 했지만 더 자세한 내용은 Part2.에서 보충하도록 하겠습니다.
2. Graph Kernel Method는 SVM에서 사용하는 Kernel Method와 개념이 동일합니다. 데이터를 새로운 공간으로 표현하는 kernel을 사용해서 그래프 데이터를 우리가 해석하기 쉬운 공간으로 투영시키는 것이죠. Kernel에 대한 개념이 어려운 것이라면 저의 자리로 찾아오시면 친절하게 설명해드리겠습니다.
3. 방향, 무방향의 차이는 임의의 노드 기준으로 근접한 이웃의 노드를 결정하는데 사용됩니다. 어렵게 생각하지 말고 node 기준으로 이웃을 정의할 때는 간선을 참고하게 되는데 이때 방향 간선이라면 그 목적지가 중요할 것이고 무방향 그래프라면 당연히 이웃 관계라고 생각하시면 됩니다.
안녕하세요.
좋은 리뷰 감사합니다.
GNN vs Network Embedding 부분에서, network embedding은 network의 구조적 정보와 콘텐츠 정보를 잘 유지하면서 low dimensional vector로 표현하는 것을 의미하고, GNN은 이 network embedding을 end-to-end 방식으로 가능하게 한다고 하시며 더욱 포텐셜이 높다고 하셨는데,
GNN은 classification이나 regression 문제를 푸는 모델이라고 하면 network embedding은 임베딩 과정을 거쳐 나온 값들을 이용하여 거기에 모델을 적용하는 느낌인 것 같습니다. 이런 차이로 network embedding과 비교했을 때 더 포텐셜이 높다고 이해하면 될까요 ?
또, graph classification 흐름도에서 pooling이 의미가 무엇인지 궁금합니다. pooling을 안했을 때와 했을 때의 차이가 무엇이 있는지요 . .
감사합니다.
network 임베딩은 저희가 기계학습에서 배우는 handcrafted feature와 비슷하게 학습이 되지 않는 방식이기 때문에 GNN이 더욱 포텐셜이 높다고 보시면 됩니다.
pooling의 의미는 어제 세미나에서 자세하게 설명했으니 자세한 설명은 생략하도록 하겠습니다.
안녕하세요 ! 좋은 리뷰 감사합니다.
Euclidean Data의 statistical propertis라는 것이 결국 local feature을 점->선->곡선 등으로 모여져 어떤 feature을 정의할 수 있음을 이야기하는 것이 맞을까요 .. .. ?
또 하나 궁금한 점은 spatial-temporal graph neural network에서 Gconv-CNN의 구성이 시간에 따라 변화하는 모든 graph에 한번씩 적용하는 것이라고 이해했는데 그렇다면 이전 time에 대한 output이 다음 GConv의 input으로 들어가게 되는 것인가요 ? ??
감사합니다.
Euclidean Data의 statistical propertis라는 것이 결국 local feature을 점->선->곡선 등으로 모여져 어떤 feature을 정의할 수 있음을 이야기하는 것이 맞을까요 .. .. ?
=> 네 그것도 있고, translation invariance 역시 statistical properties라 보시면 됩니다.
또 하나 궁금한 점은 spatial-temporal graph neural network에서 Gconv-CNN의 구성이 시간에 따라 변화하는 모든 graph에 한번씩 적용하는 것이라고 이해했는데 그렇다면 이전 time에 대한 output이 다음 GConv의 input으로 들어가게 되는 것인가요 ? ??
=> 그러한 디테일은 아직 잘 모르겠네요. Part.2를 기대해주세요!