“Historical”한 정보를 유지한다길래 키워드에 꽃혀서 읽은 논문입니다.
Introduction
일반적으로 데이터셋을 학습할 때, 분포를 학습한다는 말을 많이 하는 것 같습니다. 학습 데이터 이외의 데이터에서 모델이 예측을 못하는 이유도 그러한 데이터에 대한 분포를 학습하지 못했다는 것이겠죠. 이러한 문제를 해결하기 위해서 모델의 일반화성을 높이는 연구나, Domain Adpatation 연구들이 많이 수행되고 있습니다.
다른 도메인의 데이터에서도 이루어지는 Domain Adaptation 연구는 영상에서도 Unsupervised Video Domain Adaptation (UVDA)라는 이름으로 수행되고 있습니다. 이는 특정 도메인의 labeled video와 서로 다른 도메인의 unlabeled video를 모두 사용하여 모델을 학습해서 예측을 수행합니다. 그리고 이미지 기반의 domain alignment를 수행하기 위한 방법론들이 당연히 비디오에도 적용되고 있는데요. Temporal한 정보를 활용하는 경우의 성능이 더 좋았다고 합니다. (이는 Self-supervised learning 논문에서와 동일한 경향성을 보이는 부분이네요.) 이러한 연구 흐름이 존재하는데… Source-Free Video Domain Adaptation (SFVDA)라는 Task도 존재한다고 합니다. UVDA랑 목적은 같지만, 모델의 학습에서 labeled video만 사용한다는 점에서 차이가 있는데요. (근데 결국 unlabeled도 학습에 쓰긴 씁니다. 지도학습이 아니라는 점에서 차이가 있다는 건지… 살짝 애매하게 강조를 하네요.)
이 논문에서는 SFVDA를 해결하는 새로운 방법론으로 Spatial-Temporal-Historical Consistency (STHC)을 제안합니다. 이 방법론은 “같은 카테고리에 해당하는 비디오들은 도메인 변화와 같은 고차원 공간의 spatio-temporal한 변화에 상관없이 같은 저차원의 공간을 가진다.”는 전제조건을 가지고 이 문제를 해결하는데요.
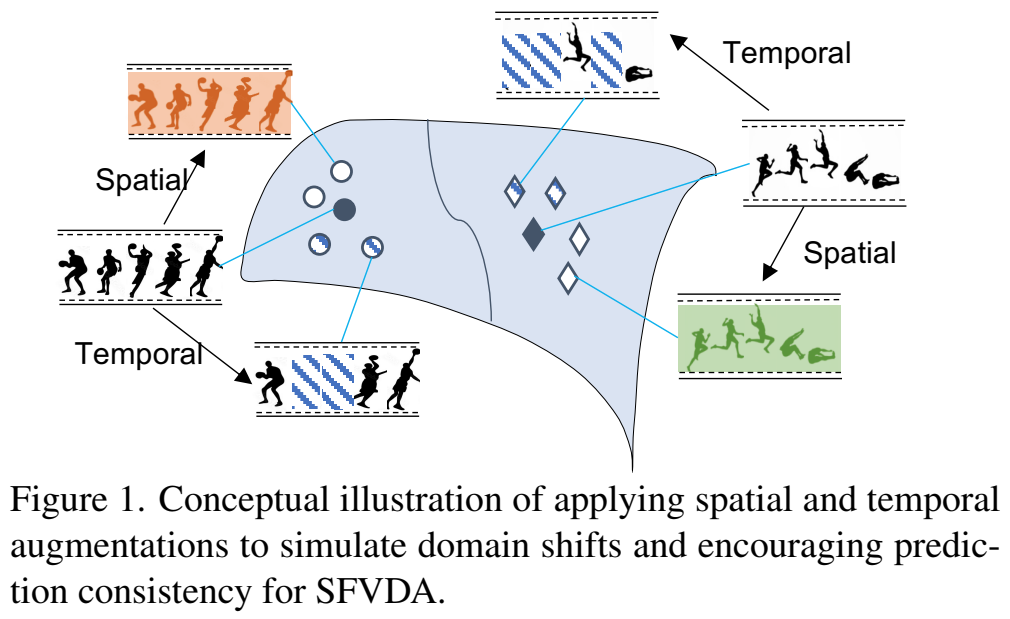
이 전제조건을 설명하는 [그림 1]을 보면 원본 영상에 변화를 줘서 도메인 변화와 같은 상황을 모사하겠다는 설명을 보이고 있는데요. 이와 같이 이 문제를 해결하기 위해 수많은 spatio-temporal variations을 만들고 이들의 분포를 학습하는 방향으로 수행합니다. 이 학습은 3가지 관점에서 진행되는데요.
- Spatial consistency (SC)
- Temporal consistency (TC)
- Historical consistency (HC)
이 관점들은 모두 모델이 일관된 예측을 수행할 수 있게 만들어주는 요소들이라고 하고, 아래에서 자세하게 설명하겠습니다. 아무튼 Contribution은 아래와 같습니다.
- 일관성(spatial, temporal, and historical) 있는 학습이 가능한 STHC 방법론을 제안함
- SFVDA에서 domain adaptation 문제를 해결하기 위해 제안된 방법론을 확장해서, 벤치마크를 확함
- 다양한 세팅에서 SFVDA의 SOTA 달성
Algorithm
M개의 라벨링 비디오가 있을 때, source dataset S = \{(X_1, y_1), (X_2, y_2),...,(X_M, y_M)\}를 사용하는 분류 모델 H가 있습니다. 비디오와 그에 해당하는 라벨이 있는 거고요. N개의 언라벨드 비디오가 있는 target dataset \tau = \{U_1, U_2,...,U_N\}가 또 존재합니다. UDVA는 둘다 동시에 학습하는거고, SFVDA는 S는 지도학습으로 학습하고, \tau는 비지도학습으로 학습하는 방식입니다. 학습할 모델 H는 백본(feature extractor)→Temporal information encoder→classifier순으로 구성되어있고, 하나의 비디오를 클립 단위로 짤라서 입력으로 사용합니다.
(모델 자체가 라벨링된 데이터 셋에서 기본적인 학습을 수행한 뒤에 일종의 fine-tuning을 unlabeled 데이터 셋에서 수행하는 것이라고 생각하면 되고, 아래에서 나오는 모든 학습은 S로 학습을 일단 한 뒤에, \tau로 학습을 어떻게 하는지에 대한 설명입니다.)
Spatial-Temporal-Historical Consistency
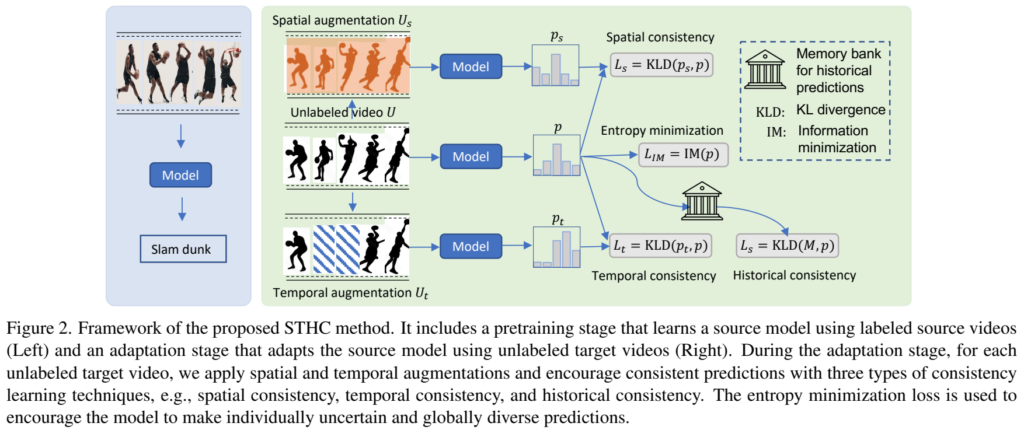
[그림 2]는 STHC 모델의 전반적인 구조에 대한 그림입니다. 보면 알겠지만 모든 Loss가 output의 확률 분포를 이용하는 KL divergence를 사용하는데요. 전제조건을 잘 생각하면서 이 구성에 대해 생각해보면 됩니다. 모델이 지도학습을 했으니까, 특정 행동에 대한 일반적인 표현력을 학습했다고 판단해보면. 예측하고자 하는 영상에 대한 분포만 학습해서 이 분포를 기존의 지도학습의 분포에 맞춰주면…? 같은 행동이니까 일관성 있는 예측을 수행하는 것을 기대해보는 겁니다.
Spatial Consistency
Unlabeled target 영상 \bar{U} = \{u_1, u_2, ..., u_K\}가 있을 때, 이 u는 영상에서 랜덤 샘플링된 n개의 프레임을 가지는 세그먼트를 생성합니다. 이 영상에 프레임 단위 augmentation(비디오에서 spatial한 뭐다 이런식으로 나오면 보통 프레임 단위입니다.)을 적용해서 \bar{U}_s = \{\psi(u_1), \psi(u_2),...\psi(u_K)\}를 입력으로 사용합니다. 여기에 적용하는 augmentation \psi가 stochastic function이라서 랜덤이라는 점을 강조하는데 아닌 것도 있을까 싶네요…?
어쨋든 뭐 다양한 spatial augmentation 기법들을 적용해서 \bar{U}의 low-dimensioanl space와 유사한 영상들을 무한히 생성할 수 있다는 건데… 학습을 오래 돌리는 것(15epoch 학습 수행)도 아니고 아무리 분포를 학습한다고 해도 영향이 그렇게 클 것 같지는 않네요.
그래서 spatial consistency를 학습하기 위한 Loss는 L_s = KLD(H(\bar{U}_s), H(\bar{U}))인데요. 원본 영상과 augmentation된 영상의 데이터 분포를 학습하면서 모델이 spatial한 변화가 일부 생기더라도 같은 분포를 가지는 결과값을 생성하도록 학습합니다.
Temporal Consistency
spatial consistency랑 유사하게 여기서도 temporal consistency를 유지하는 방법으로 temporal한 augmentation을 적용합니다. 똑같이 Unlabeled target 영상 \bar{U}가 있을 때, stochastic한 temporal augmentation을 적용해서 \bar{U}_t = \{\phi(u_1),\phi(u_2),...,\phi(u_K) \}를 생성합니다.
여기서 적용되는 augmentation은 dropout이 있는데요. 이건 이제 연속적인 프레임에서 일부 프레임들이 제거되어도 motion 정보는 어느정도 보존이 될 것을 기대하기 때문에 적용된건데요. Loss자체는 L_t = KLD(H(\bar{U}_t), H(\bar{U}))로 spatial consistency와 유사하게 구성됩니다.
결국은 유사하게 원본 영상과 augmented 된 영상의 low-dimension space는 유사하게 가져가는 방식인데, 특정 프레임이 제거되면서 모션 정보가 선형적이지 않게 됩니다. 그래서 좀 더 난이도가 있는 예시를 만들 면서, 모델이 다양한 동적인 움직임에 대응할 수 있게 된다고 주장합니다.
Historical Consistency
Temporal consistency를 보조하기 위해 사용하는 것이 historical consistency라고 보면 되는데요. Temporal consistency의 원리를 생각해보면 inter-segment consistency만 고려한다고 합니다. (일부 모션 정보가 누락되어도 해당 세그먼트가 항상 같은 분포를 가지도록 학습을 하기 때문)
그래서 historical prediction이라는 것을 도입해서, 세그먼트 내의 예측값의 intra-segment consistency를 유지하도록 합니다. 영상 내에서 이전 시퀀스의 예측값들을 메모리 뱅크에 저장해서, 현재 예측값과 KL divergence를 계산합니다.
p_u가 U로 부터 샘플링된 예측 결과라고 하면, L_h = \mathbb{E}_{p_u\sim M} \left [ KLD(p_u, H(\bar{U})) \right ]와 같이 Loss가 만들어지는데요. 메모리 뱅크에 있는 모든 예측 결과와 원본 영상의 예측 결과의 분포는 동일해지도록 학습을 수행합니다. 논문에서는 이전 2개의 예측 값까지 비교하는게 가장 일반화된 성능 값을 보여주었다고 하네요.
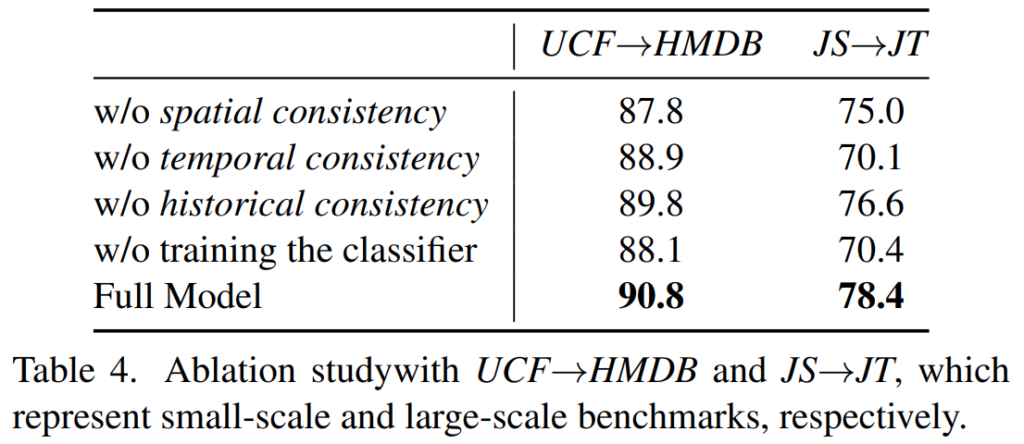
사실 이부분에 대해서 왜 성능이 오르는지에 대한 공감이 어렵네요. 메모리 뱅크의 크기에 대한 ablation이 없는건 그럴 수 있고, [표 4]를 통해 historical consistency가 빠질 경우 성능이 떨어진 다는 것은 보여주고 있습니다.
하지만 historical consistency가 무엇을 학습하는지 조금 모호한 것 같습니다. 이전 예측값의 분포를 현재 예측값의 분포와 동일하게 한다고 하더라도, 이전 예측값의 영상과 현재 예측값의 영상이 다른 액션을 다룰 확률이 높은데요. (실제로 메모리 뱅크 Q의 값이 2가 최적인 것을 보면…) 이럴 경우 영상 내의 motion 정보를 본다고 해도 서로 다른 분포를 가질텐데 이렇게 학습이 수행되는게 무엇을 학습하는지 명확한 설명이 필요한 것은 아닐까… 라고 생각합니다. 물론… 좀 해보고 이게 정말 뭔가 일관된 표현력이 있다 싶으면 저도 한번 써먹어보게 기억 잘 해놔야겠네요 ㅋㅋ
Overall Learning Objective
최종 Loss는 3가지 Consistency를 유지하기 위한 Loss를 다 더해서, L = L_{im} + \alpha(\mathbb{E}_{\bar{U}\sim \tau}(L_s+L_t+L_h))와 같이 사용합니다. 못보던 Loss가 하나 더 있는데, L{im}은 information maximization loss인데요.
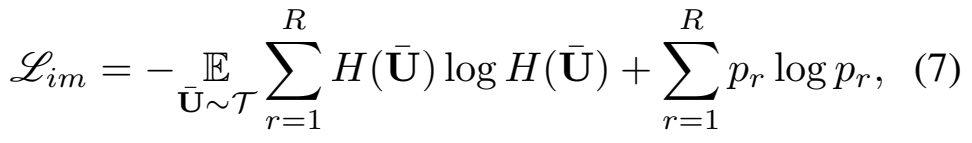
[수식 7]의 앞 뒤 연산을 구분해봅시다. 먼저, 앞의 연산은 cross-entropy의 엔트로피를 줄여서, 모델이 조금 더 예측값에 확신도를 높이도록 합니다. 그리고 뒤의 연산은 p의 엔트로피를 크게 만드는데요. p는 p=-\mathbb{E}_{\bar{U}\sim \tau}H(\bar{U})로 예측 결과의 평균 예측값을 의미합니다. 그렇기 때문에 모델이 모든 클래스에 대해 골고루 예측을 수행하도록 유도합니다.
추가적으로 Partial Domain Adaptation (PDA), Open-Set Domain Adaptation (OSDA), Black-Box Model Adaptation (BBMA)와 같은 Task에서의 확장이 가능한게 논문의 contribution 중 하나라서 확장 방법에 대한 설명이 있는데, 관심있는 분들이 찾아보시는 것이 좋을 것 같네요.
Experiments
실험 세팅이 몇가지가 있어서 간단하게 소개하고 넘어가겠습니다. UCF-HDMB는 이제 UCF에서 지도학습하고 HMDB에서 비지도학습 하는 셋이고, 클래스가 다른 경우에는 겹치는 클래스에 해당하는 영상만 사용했다고 보면 됩니다. UCF-Kinetctics도 동일하고 SportsDA benchmark에서 사용하는 세팅이고 Sport-1M 데이터 셋 까지 포함입니다. 나머지는 그냥 Cross-domain 세팅에서 실험하는 데이터 셋이라고 보면 될 것 같습니다.
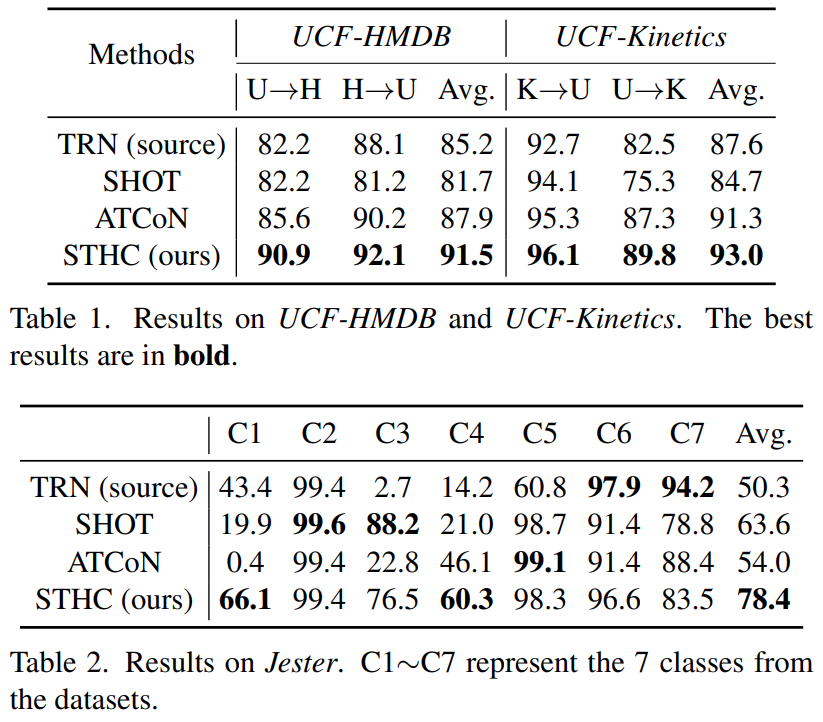
그래서 실험 결과를 보면, 위의 두 표와 같은데요. 화살표 방향이 있다는게 이제 화살표 출발점이 지도학습으로 학습한거고, 화살표 도착점이 비지도학습으로 학습하고 평가한 결과입니다. 클래스별 성능이 좀 다르긴 하지만 평균적으로는 높은 성능 향상을 보입니다.
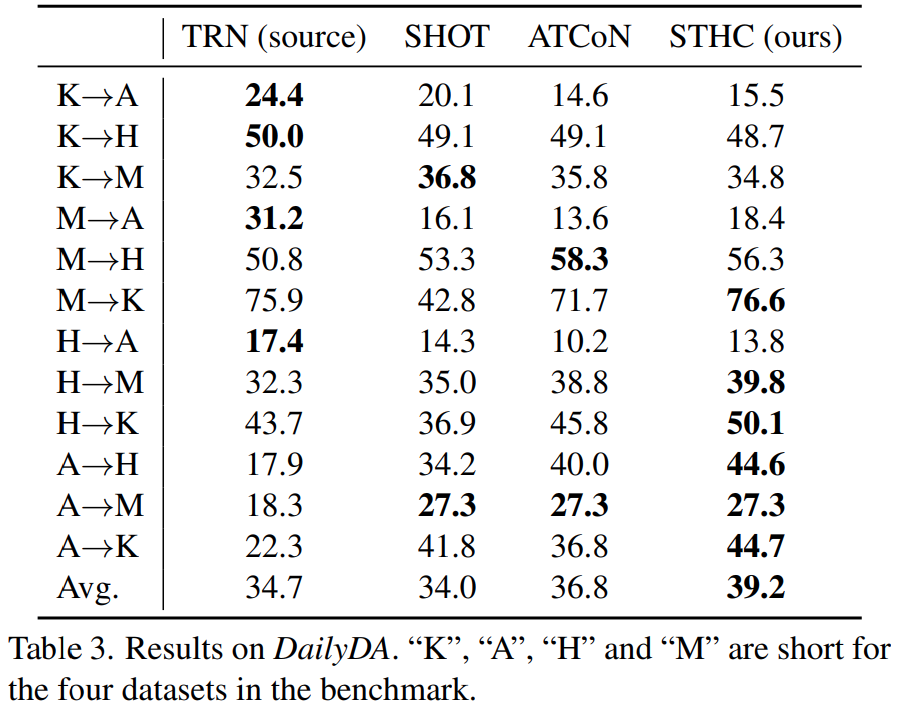
표 3은 좀 다른 양상을 보여줍니다. 학습 방식에 따라 성능이 좀 차이가 발생하는데요. 벤치마크 자체가 어려워서 지도학습을 했을 때도 일부 라벨에서 정확도가 30%도 안되는 경우가 발생해서 그렇다고 합니다. 제안하는 방법론 자체가 지도학습에서 정확도가 낮으면 학습에 의미가 없어서, 데이터 분포를 학습할 때 에러가 누적되기 때문이라고 하네요.
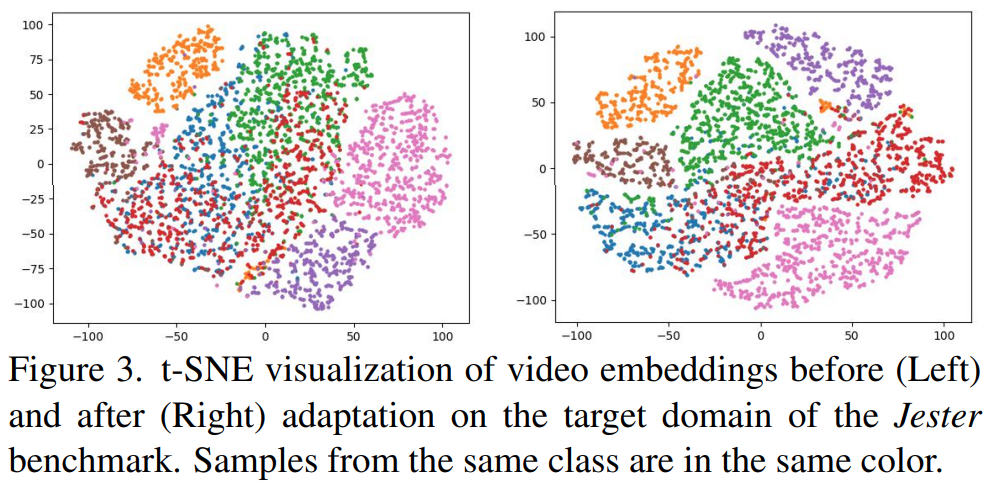
[그림 3]은 t-SNE로 보여주는 임베딩 결과입니다. 데이터 분포를 중점적으로 학습한 결과를 보여주는 건데, 타겟 데이터셋에 비지도 학습 수행 전후로 결과를 보여주는데… 확실히 구분력이 생기긴 했습니다.
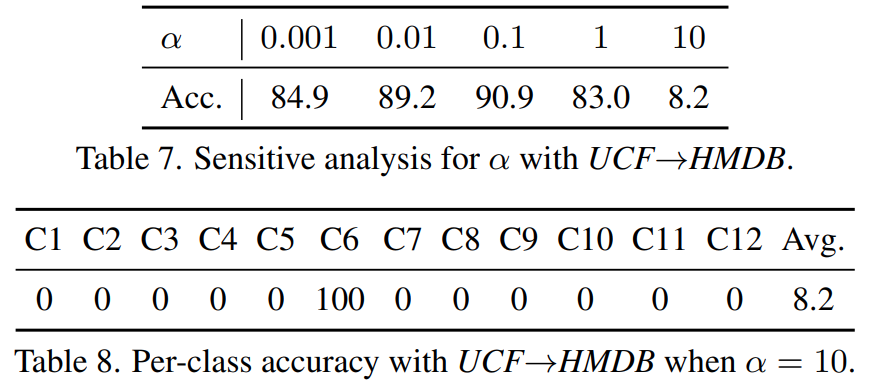
[표 7]은 Loss의 하이퍼 파라미터 $\alpha$에 따른 성능 차이를 보여주는 ablation인데요. 이 $\alpha$가 결국은 데이터 분포로 학습한 결과를 얼마나 Loss에 크게 반영할지에 따른 결과인데요. Information minimization Loss는 데이터 끼리의 분별력을 학습하고, Consistency loss는 데이터의 분포 자체를 유사하게 만드는 것이기 때문에 역할이 달라서 적당한 밸런스를 유지하는 것이 중요함을 보입니다.
Conclusion
Historical Consistency에 대한 의구심이 있긴 하지만, 정말이라고 하면 적용해볼 만한 부분이 있다고 생각은 합니다. 사실 아쉬운건 final version인데 수식에도 오타있고, 용어 통일이 조금 안되있는 것 같습니다. 조금 아쉬운 논문 같은데… 이 분야 자체를 처음 봤으니 그렇게 생각하는 것이라 믿고… 넘어가려고 합니다.