image retrieval의 근본이라고 할 수 있는 r-mac 논문 리뷰입니다. VPR 논문을 읽고 보니 retrieval의 기본적인 방법론에 대해 정리해야겠다 싶어 2주간 해당 분야의 논문을 리뷰하고자 합니다.
abstract
CNN으로 뽑은 representation은 이미지 검색 분야에서 좋은 discriptor로 사용된다. 그리고 그 성능은 cnn이전에 사용되던 short-vector representation의 성능을 outperform한다. 그러나 이러한 CNN모델은 geometry-aware re-ranking 방법론에서는 compatible하지 않다. 이러한 work는 CNN으로부터 추출된 same primitive 정보를 사용하여 retrieval의 initial search와 re-ranking과정을 revisit한다. 저자들은 새로운 feature vector를 제안하였는데 이 벡터는 네트워크에 multiple입력 없이 several image region을 인코딩했다. 또한 integral images를 convolution layer의 activation에 존재하는 max-pooling을 handle하도록 확장하였다. resulting bounding box는 image reranking에 사용됨. 결과적으로 저자들이 제안한 feature vector로 인해 CNN-based recognition pipeline에서 성능 향샹을 이루었다. 실험은 Oxford5k, Paris6k로 진행되었으며 각 벤치마크의 sota를 달성하였다.
Introduction
Image retrieval은 일반적으로 데이터베이스 내의 모든 이미지에 대해 query 이미지와의 similarity를 구하는 Filtering(Initial Ranking)과 높은 유사도를 가진 이미지들의 retrieval 결과를 개선하는 Re-Ranking의 두 단계로 진행되었습니다. 논문이 나올 당시의 image retrieval task의 sota는 BoW를 사용하는 방식이었는데요, 이는 locally invariant 한 feature와 large visual codebook을 사용하는 방식이었다고 합니다.
Background
논문에서 제안하는 r-mac을 설명하기 앞서 mac에 대해 설명드리겠습니다.
mac은 하나의 이미지를 표현하는 특징 벡터로 이미지의 feature map에 spatial max pooling을 진행하여 얻을 수 있습니다. pre-trained CNN에서 FC레이어를 제거하고 W_1×H_1크기의 이미지 I를 입력하면 Convolution의 출력은 W\times H\times K 크기의 tensor이며 ReLU가 사용되어 tensor의 각 요소는 음수가 아님을 보장받게 됩니다.
이 tensor는 채널 수 K에 대해 2D vector \mathcal X={\mathcal X_i}, i=1...K의 집합으로 표현하는데, 여기서 \mathcal X_i는 valid spatial location \Omega에 대한 i번째 activation을 나타내는 2D tensor이고, \mathcal X_i(p)는 특정 위치 p에서의 응답입니다. 따라서 모든 위치에 대한 spatial max-pooling으로 구성된 특징 벡터는 아래의 식(1)과 같이 나타낼 수 있습니다.
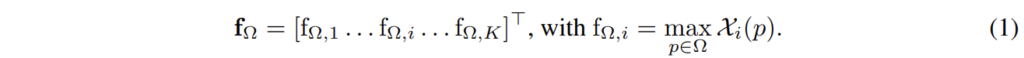
위의 설명만 듣고 보면 다소 복잡하게 느껴질 수도 있으나 결론적으로 f_{\Omega}는 크기가 W\times H\times K인 feature map에서 각 채널 별로 max pooling을 수행하여 1\times K크기의 벡터를 구한 것을 의미합니다.
Maximum activations of convolutions (MAC)
앞서 mac이 retrieval에서 사용되는 특징 벡터라는 언급을 했었는데요, image retrieval에서 이미지의 similarity를 비교하기 위해 각 이미지를 대표하는 특징 벡터를 추출하고 두 벡터간의 코사인 유사도를 측정하는 방식을 사용합니다. 이때 특징 벡터로서 위의 MAC을 사용할 수 있습니다.
MAC은 W \times W크기의 영역에 대해 max pooling을 적용한 것이기 때문에 activation의 위치 정보를 encoding하지 않습니다. 또한 각 convolution 필터에 대해 “local” response의 최댓값을 encoding하였으므로 translation과 scale 변화에 invariant하다는 특징이 있습니다.

위의 [그림 2]는 각 이미지 쌍에 대해 두 이미지의 similarity에 가장 크게 기여한 5개의 MAC components의 receptive field를 시각화 한 것입니다. 이 patch들은 동일한 object를 나타내거나 반복되는 구조에 의해 서로 대응되는 것을 확인할 수 있습니다.
Encoding Regions Into Short Vectors
MAC 방식은 max pooling을 사용하였으므로 translation invariant하다는 특성이 있습니다. 그러나 전체 영역에 대한 max activation만을 고려하게 되므로 이미지의 local한 특징의 손실이 발생합니다. 이에 저자들은 앞서 설명드린 mac을 기반으로, full 이미지가 아닌 관심 영역을 설정하여 해당 영역의 representation을 추출하는 r-mac이라는 방법을 제안하였습니다.
Region feature vector
식(1)이 나타내는 벡터 f_{\Omega}는 단순히 채널 별로 max pooling을 수행한 것으로 이미지 I 전체에 대한 특징을 나타냅니다. 이 논문에서는 이미지 전체가 아닌 관심 영역 \mathcal R을 고려하는 regional feature 벡터를 아래의 식(2)와 같이 정의합니다.
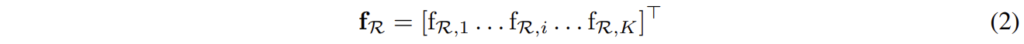
이때 \mathbf f_{\mathcal R}의 요소들인 \mathbf f_{\mathcal R,i}=max_{p \in \mathcal R}\mathcal X_i(p)는 영역 R에서 i번째 채널의 최대 activation 값을 의미합니다.
R-MAC: regional maximum activation of convolutions
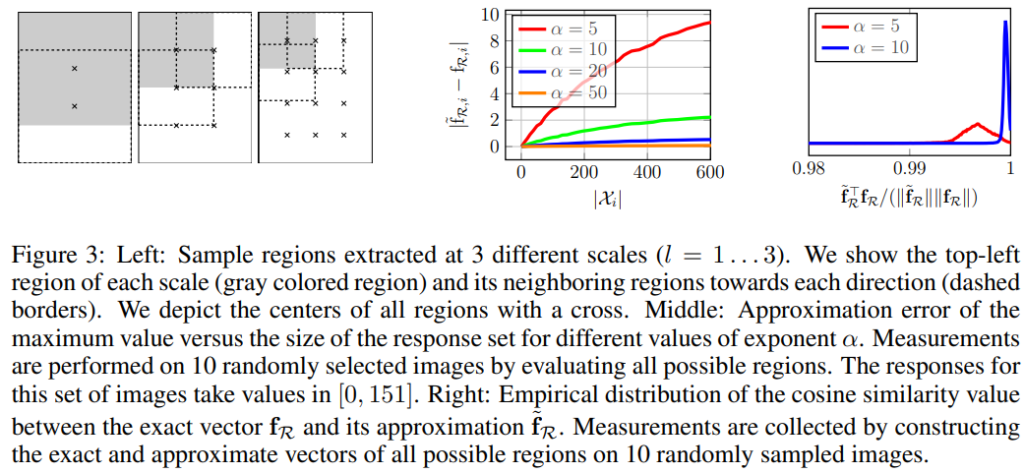
저자들은 다양한 scale의 R을 통해 이미지의 local영역의 representation을 추출하려고 하였습니다. 총 L단계의 scale(논문에서는 L=4까지 실험 진행)을 sampling하는 경우, 가장 큰 scale은 l=1이며, 이는 이미지의 크기가 W\times H일 때 한 변의 길이가 min(W, H)인 정사각형 영역으로 정의하였습니다. l이 1, 2, 3…으로 증가함에 따라 한 변이2\min(W, H)/(l+1)인 영역 l\times (l+m-1)개를 sampling하였습니다. [그림 3]의 가장 왼쪽 그림이 l=1, 2, 3일 때의 R을 나타낸 것으로 회색 영역이 sampling되는 영역 R이고 ‘x’표시는 각 영역의 중심을 나타냅니다.
각 영역에서 \mathbf f_{\mathcal R}을 계산하고 나면 K size 벡터가 sampling되는 영역의 개수만큼 생성되는데요, 이를 하나의 벡터로 만들어주기 위해 각각에 l2 norm과 PCA를 적용한 뒤 모두 더하고 다시 l2 norm을 적용하였습니다. 최종적으로 생성된 크기가 K인 벡터를 R-MAC이라 하며 MAC과 동일한 차원을 가지는 동시에 더 나은 성능을 확보하였다고 합니다.
Object Localization
Approximate integral max-pooling
- Approximate max-pooling
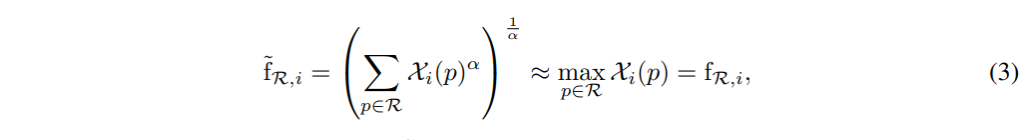
수식 (3)은 \mathbf f_{\mathcal R}을 generalized mean을 이용해 근사시킨 것입니다. 이때 \mathcal X_i의 모든 원소는 0보다 크거나 같고, \alpha>1인 파라미터 \alpha는 \alpha→+∞일 때 \tilde{f}_i→f_i가 됩니다.
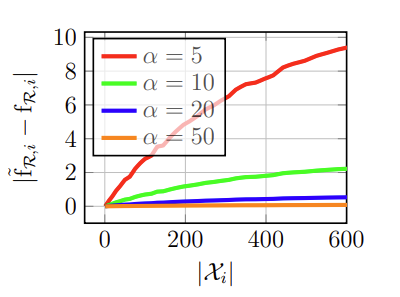
위의 그래프는 여러 \alpha값에 따른 \mathcal X_i의 원소의 개수에 대한 max값과 max의 근사값의 차를 나타낸 것으로 \alpha값이 증가할 수록 근사값이 정확해지고, 원소의 개수가 많아질수록 근사값의 정확도가 떨어지는 것을 볼 수 있습니다.
- Integral image
위와 같은 방식으로 max값을 approximation하면 이제 integral image를 사용하여 영역 \mathcal R에 정의된 \mathbf f_{\mathcal R}를 근사화할 수 있습니다. integral image란 아래의 그림과 같이 (0,0)에서 해당 픽셀까지의 합으로 구성된 이미지입니다. 좌측의 original image내에 존재하는 일정 영역의 합을 구한다고 할 때, 우측의 integral image의 네 픽셀값으로 나타낼 수 있습니다.

이를 이용하여 \mathcal X_i(p)^{\alpha}, p\in \mathcal R인 2D Tensor의 integral image를 생성한다면, 식(3)의 \sum_{p\in \mathcal R} \mathcal X_i(p)^{\alpha} 부분을 빠르게 구할 수 있습니다.
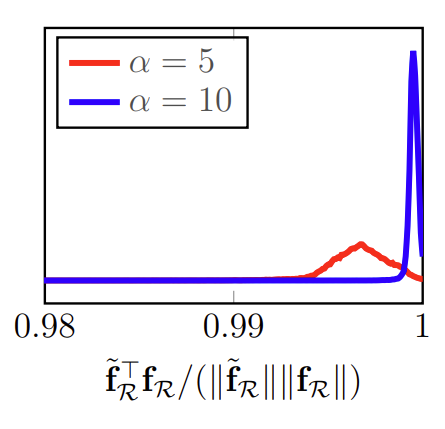
그렇다면 수식(3)을 사용하기 위해 파라미터 \alpha값을 정해야 하는데요, 저자들은 랜덤으로 고른 10개의 이미지에서 원래의 \mathbf f_{\mathcal R}와 근사값인 \tilde{\mathbf f}_{\mathcal R}간의 cosine similarity를 측정하였으며, 아래의 모든 실험에서 \alpha =10으로 설정하였습니다. 아래의 그림은 \alpha가 5, 10일때의 cosine similarity를 나타냅니다.
Window detection
위에서 설명한 r-mac은 이미지를 영역별로 max pooling하여 n개의 K size 벡터를 구하고 이를 더하여 생성된 discriptor로 filtering을 거쳐 상위 k개의 이미지를 선별합니다. 그 다음에는 k장의 이미지 내에서 re-ranking을 진행하는데요, 이때는 n개의 영역을 모두 사용하는 것이 아니라 각 영역 중 query와 가장 유사한 영역\mathcal{\hat R}을 선별하고 해당 영역에 대해서만 re-ranking을 진행합니다. query 이미지의 MAC 벡터가 q일 때 \mathcal{\hat R}은 식(4)와 같습니다.
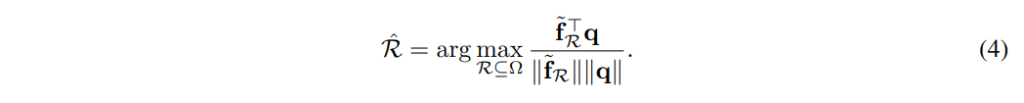
Experiments
실험 부분에서는 r-mac의 retrieval 성능과, AML의 localization accuracy를 평가하며, 마지막으로 retrieval re-ranking에 AML을 적용하였습니다.
Retrieval and re-ranking
- retrieval performance
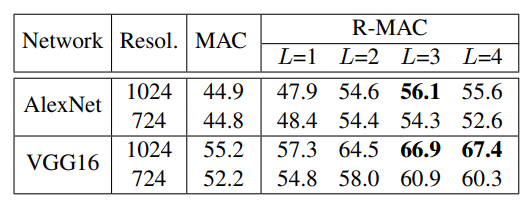
위의 표는 Oxford5k 데이터셋에서 MAC과 R-MAC feature를 사용한 image retrieval 성능을 비교한 표입니다. MAC은 l2 normalize한 후 PCA를 적용하여 low demension으로 변환 후 다시 l2 norm을 적용하여 추출한 벡터이며, R-MAC은 본문에 설명된 것과 같습니다.
Resol.은 input 이미지의 해상도를 의미하며, 1024가 원본 이미지의 size라고 합니다. 저자들은 서로 다른 해상도의 이미지를 input으로 하여 re-ranking성능을 비교하였으며, 원본 이미지의 크기인 1024에서 더 높은 성능을 보이는 것을 확인할 수 있습니다.
- re-ranking
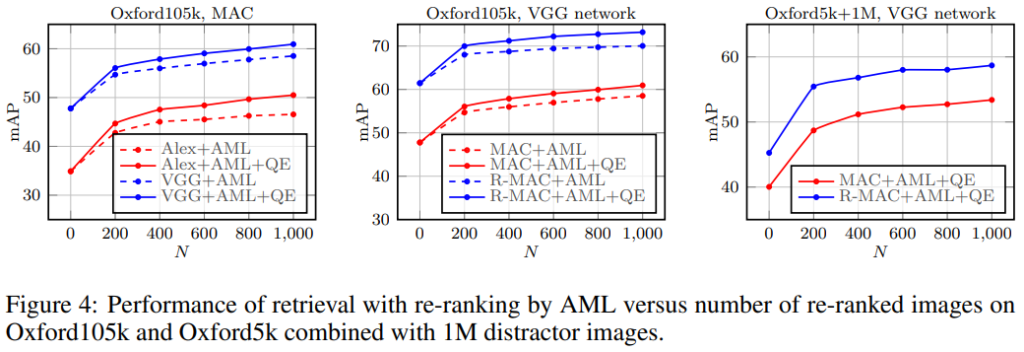
[그림 4]의 왼쪽의 그래프는 CNN backbone에 따른 Oxford105k 데이터셋에서의 re-ranking performance를 비교한 것으로, AlexNet보다 VGG를 사용하였을 때 mAP가 더 높게 나온 것을 확인할 수 있으며, AlexNet이 VGG보다 QE를 적용하였을 때 성능 향상폭이 큰 것으로 확인할 수 있습니다.
[그림 4]의 중앙 그래프는 마찬가지로 Oxford105k데이터를 사용하였으며, backbone을 pretrained VGG로 고정시킨 뒤 MAC과 R-MAC간의 성능을 비교한 결과입니다. mac과 r-mac의 성능 차이를 통해 r-mac의 local 정보가 retrieval 성능의 향상을 가져왔음을 확인할 수 있습니다.
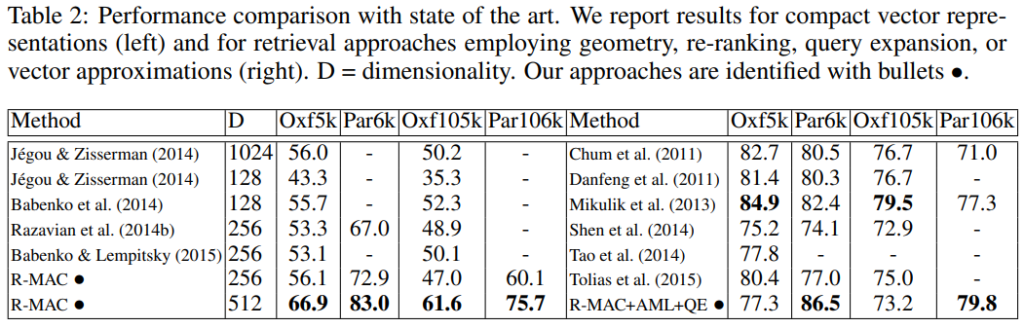
Comparison to the state fo the art
[표2]는 sota방법론들과 r-mac의 retrieval 성능 비교 결과입니다.