안녕하세요, 로보틱스 팀 양희진 입니다. 이번에도 6D Pose Estimation 논문을 리뷰해보았습니다.

제가 지금까지 리뷰를 진행했었던 방법론들은 비교적 해당 분야에서 오래된 방법론들 입니다. 데이터셋 촬영을 계획이 7월 전에는 진행될 예정에 있기 때문에 데이터셋에 대한 서베이를 진행하였습니다. 또한 촬영된 데이터셋에 대한 추정 결과를 확인하기 위해 베이스라인을 잡아야 하는 상황에 있어 데이터셋 서베이 중 BOP Benchmark 라는 챌린지를 작년에 진행했다는 것을 알게 되었습니다.

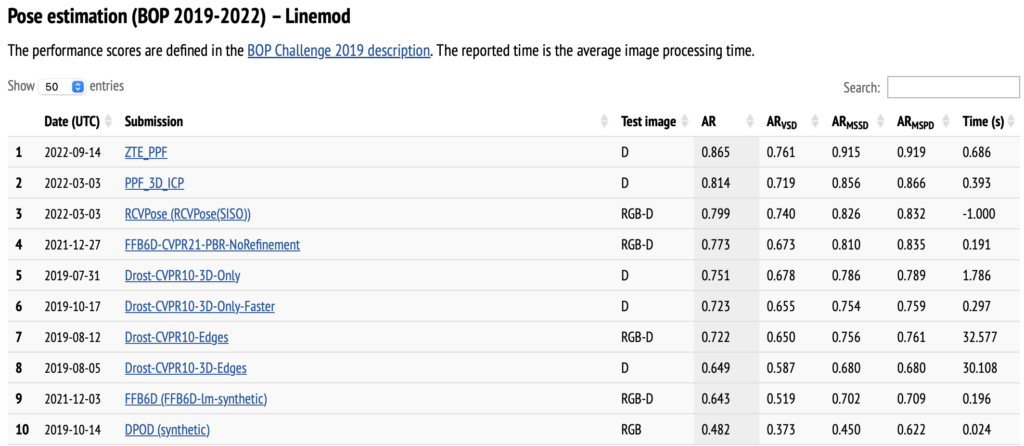
해당 사이트에서 저희가 URP때 KAIST PD 평가를 위해 사용하였던 EvalAI 사이트처럼 리더보드 형식으로 진행되었던 것을 확인할 수 있었고, AR(Average Recall)이 0.70이상 달성한 방법론이면서 해당 리더보드에서 RGB-D에 대해서 SOTA를 달성한 RCVPose에 대해 리뷰를 해봤습니다. 아쉽게도 RCV는 Robotics Computer Vision은 아니고 Radial K(C)eypoint Voting를 RCV라고 했네요.

왜 저렇게 지었는지는 잘 모르겠습니다. 뭔가 이름을 뺏긴 느낌입니다.🫠

Background Knowledge

• Andre’s circle redering algorithm
  • 원을 그리기 위한 알고리즘
  • 원의 픽셀을 렌더링 하는 데 사용됨
  • 각 픽셀에 대해 중심과의 거리를 계산하므로 비교적 직관적임

Abstract

• 기존의 방법론보다 더 적은 수의 키포인트를 disperse시켜 좀 더 정확한 voting 방식을 제안
• 해당 voting 방식은 포인트 사이의 거리를 기반으로 하고 1D quantity 이전에 진행했던 regression 한 2차원 및 3차원 벡터와 offset quantity보다 더 정확하게 regression 할 수 있어 좀 더 정확한 keypoint를 localization 할 수 있음 → occlusion에 효과적임
• 학습은 각 RGB 픽셀의 depth mode에 해당하는 3D point와 object frame로부터 3개의 disperse keypoint set의 거리를 추정하도록 CNN을 학습하도록 함
• 예측은 3D point를 중심으로 추정된 거리와 동일한 반지름의 구를 생성함
• 해당 구의 표면은 voting을 통해 3D accumulator space를 점진적으로 증가시키면서 해당 공간의 peak가 keypoint의 위치를 나타냄
• 이러한 radial voting 방식은 vector, offset 방식보다 더 정확하고 keypoint를 disperse에 용이함

1. Introduction

다들 아시다시피 물체의 pose estimation을 하는 것은 로보틱스 분야에서 꼭 필요한 분야입니다. 하지만 occlusion, clutter, sensor noise, illumination, symmetry에 여전히 어려움을 겪고 있는 상황입니다. 이러한 문제들을 3D 모델과 이미지의 feature 사이의 correspondence를 고려하여 해당 문제들을 해결했었는데, 해당 경우에는 hand-crafted으로 만든 feature에 의존할 수 밖에 없습니다. 즉, 물체가 featureless하거나, scene이 매우 복잡하거나, occlusion이 있는 경우 결과가 좋지는 않았습니다. 하지만 이러한 hand-craft 방법은 딥러닝이 해당 문제들을 해결해주죠. 네트워크 구조를 통해 학습을 하면서 입력 이미지로부터 6D pose estimation를 통해 직접 regression을 진행합니다. YOLO6D와 같은 논문에서는 2D keypoint를 regression하고 PnP 알고리즘을 이용하여 6D pose estimation을 하는 CNN-based 방법이 있습니다. 예전에 제가 리뷰를 했었던 PoseCNN에서는 keypoint 좌표를 직접 regression하는 방법 대신에 keypoint에 voting을 하는 방법은 물체가 occlusion이 부분적으로 발생했을 때 매우 효과가 있는 것이 검증되었습니다. 해당 방법론들은 2D 픽셀의 위치를 3D keypoint와 연관시키는 고유한 geometric quantity를 regression하고 각 픽셀에 대해 해당 quantity를 accumulator space로 casting합니다. 픽셀당 독립적으로 voting이 누적이 되므로 해당 방법을 통해 특히 occlusion에 더 강인해지면서 성능을 향상시킬 수 있게 되었습니다.

이러한 voting 방식은 최근에 큰 성과를 보였지만 keypoint에 voting을 하기 위해 quantity를 계산하는 2D voting의 경우에는 2채널, 3D voting의 경우 3채널의 activation map의 regression이 필요하게 됩니다. 여기서 activation map은 voting된 quantity를 저장한 이미지 형태의 tensor를 의미한다고 합니다. 해당 activation map의 차원은 어떻게 될까요? 앞서 언급한 regression되는 geometric quantity에 따르게 되면서 각 채널의 estimation error은 점점 복잡해지는 경향이 있게 됩니다. 당연히 estimation의 error가 커지게 되면 keypoint에 대해 voting을 진행할 때 high-dimension의 activation map의 localization 정확도가 떨어지게 됩니다. 저자는 RGB-D 데이터셋으로부터 1D activation map을 regression시켜보는 실험을 진행하면서 좀 더 정확한 localization을 가능하게 하는 새로운 radial voting 방식에 영감을 주었다고 합니다. 그리고 keypoint localization의 정확도가 높아지면 keypoint set를 더 많이 disperse 할 수 있어 transformation에 대한 추정 정확도를 올릴 수 있으므로 결과적으로 6D pose estimation에 대한 성능이 향상 됩니다.

저자는 해당 방법론을 RCVPose 라고 이름을 지었네요. 제안된 RCVPose는 3D keypoint와 각 2D RGB 픽셀에 해당하는 3D scene point의 거리를 추정하기 위해 CNN을 학습합니다. inference 때는 해당 거리가 2D scene 픽셀에 대해 추정이 되고 해당 추정은 1D quantity이므로 regression한 high-dimension quantity보다 더 정확하다고 합니다. 해당 내용은 앞서 언급한 estimation error가 차원이 증가하면서 복잡해지게 되는데 activation map localization의 정확도를 떨어뜨리는 것에 대한 내용을 말하는 것 같습니다. 각 픽셀에 대해 이러한 regression distance와 동일한 radial sphere가 해당 3D scene point의 중심에 위치하게 됩니다.

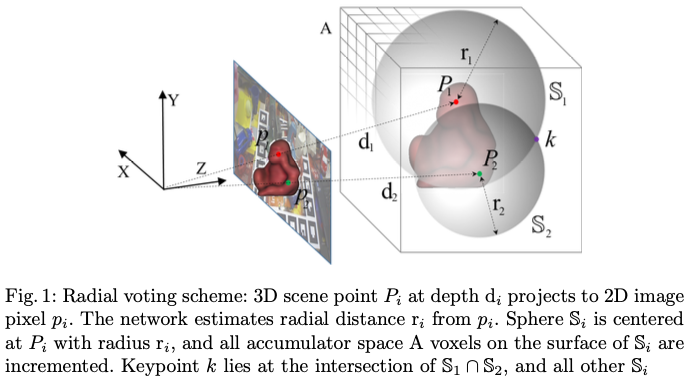
그림1을 보시면 위 내용이 이해되실 거라고 생각합니다. 해당 구의 표면과 교차하는 3D accumulator space cell(voxel)이 커지면서 peak는 keypoint의 위치를 나타내게 됩니다. 최소 3개의 keypoint에 대해 이와 같은 과정을 거치면 물체의 6D pose estimation를 unique하도록 recover할 수 있다고 합니다.

Contribution

• 1D regression-based radial voting 방식이 2D, 3D regression-based 방식보다 더 정확한 것을 실험을 통해 검증함
• radial voting 방식에 기반한 6D pose estimation 방법인 RCVPose를 제안

2. Related Work

딥러닝 기반의 6D pose estimation 방법의 종류는 viewpointed-based, keypoint-based, voting-based로 총 3개가 있습니다. 해당 내용들을 다시 상기하기 위해 다루어보았습니다.

Viewpoint-based methods

3D 또는 projection된 2D 템플릿을 일치시켜 pose estimation을 진행합니다.

Pix2Pose에서는 gerative autoencoder architecture를 사용하였는데 이미지 간에 translation에 대한 과정을 수행하는 것과 유사하게 RGB이미지를 3D 좌표로 변환하기 위해서 GAN을 사용했고 생성된 픽셀 단위의 예측을 여러 단계에 걸쳐서 사용하여 2D-3D correspondence를 만들어서 RANSAC-based PnP를 통해 pose estimation을 하였습니다.

최근에는 multi-task CNN-based encoder/multi-decoder architecture로 annotation이 없는 실제 RGB-D 데이터에 대해 self-supervised 방법을 통해 렌더링을 하고 최적의 align을 찾는 방법도 제안되었습니다.

Keypoint-based methods

지정된 물체 중심의 keypoint를 detection하고 최종 pose estimation을 위해 PnP를 적용합니다.

2D keypoint 위치에서 local pose estimation을 위해 물체가 보이는 부분에 대해서 사용하는 segmentation-based 방법론도 있습니다. 해당 방법론은 YOLO-based 구조로 confidence score를 사용하여 이미지와 물체의 3D 모델 간의 2D-3D correspondence를 설정하였습니다. 이전에 이승현 연구원님께서 리뷰해주신 DPOD에서는 입력 이미지와 사용 가능한 3D 모델 간의 dense 2D-3D correspondense map을 추정하는 dense pose object detector를 제안하여 PnP와 RANSAC을 사용하여 6D pose estimation을 recorver하는 방법도 있습니다.

Voting-based methods

해당 voting 방식은 pose estimation에서 가장 오래된 방법론이라고 합니다. 인공지능이라는 것이 뜨기 전에는 Hough transform, RANSAC 이후 clustering하고 이미지 retrieval과 같은 방법이 6D pose estimation을 localization하는 데 일반적으로 사용이 되었습니다. 그 당시에는 hand-crafted 방식으로 만든 feature descriptor가 필요했었고 voting은 3D point cloud 이미지로 확장되어 affine-invariant pose를 추정할 수 있게 되었다고 합니다.

3. Methodology

3.1. Keypoint Voting Scheme Alternatives

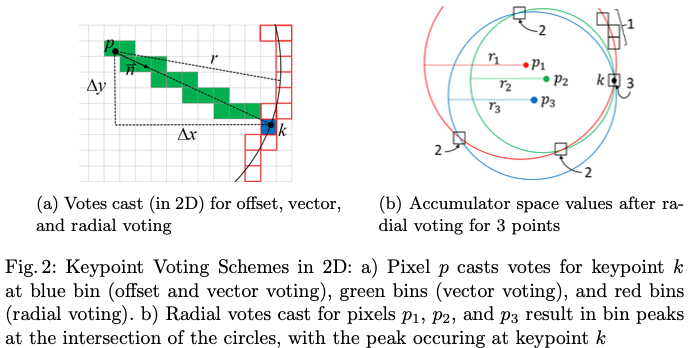
해당 논문의 contribution인 keypoint voting 방식의 대안을 살펴보도록 하겠습니다. 앞서 언급한 최소 3개의 keypoint voting 방식이 그림2(a)에 2D으로 나타냈습니다. 이미지 픽셀 p와 keypoint k를 추정할 수 있습니다.

해당 픽셀은 voting이 이루어지는 voxel space 요소인 accumulator space bin을 나타내게 됩니다. voxel space는 처음에는 비어있는 상태로 점점 증가하는 형태로 보입니다. offset에 대한 voting은 어떻게 진행될까요? 해당 그림의 \Delta x, \Delta y의 값은 네트워크의 학습을 통해 추정됩니다. 해당 값들은 k가 포함된 accumulator space bin(파란색)을 reference로 하기 위해 p를 offset으로 사용하여 해당 값을 증가시키는 데 사용된다고 합니다. 또는 vector voting에서는 방향 \vec n이 추정되고 \vec n과 교차하는 모든 구간(초록색이랑 파란색)이 커지게됩니다. 마지막으로 radial voting에서는 p를 중심으로 radius r의 원의 둘레와 교차하는 모든 구간(빨간색)이 증가하게 됩니다. 모든 이미지 픽셀에 대해 반복하면 모델의 inference에 의해서 추정된 quantity가 충분할 정도로 정확하면 어떤 방식을 사용하든 k를 포함하는 bin에 maximum accumulator space값이 포함된다고 합니다.

그림2(b)는 radial voting으로 생성된 원이 3개의 이미지 픽셀에 대해 설명되어 있습니다. 각 영역에는 원이 서로 교차하는 개수가 포함되며 해당 그림에서 peak 값은 3이므로 해당 영역에서 keypoint k의 위치를 나타내게 됩니다. 즉, 3가지 voting 방식은 3D space로 확장이 되게 되는데 이때 accumulator space은 voxel grid이고 offset에 \Delta z 요소도 포함하고 \vec n은 3차원 벡터를 의미합니다. radial voting방식은 2차원 원이 아닌 3차원 구의 표면에 대해 voting을 진행하는 과정을 의미합니다.

p_i는 2D 이미지 좌표(u_i, v_i)와 해당 3D 카메라 프레임 좌표 (x_i, y_i, z_i)를 가지는 RGB-D 이미지 I의 픽셀을 의미합니다. k^\theta_j=(x_j, y_j, z_j)는 6D pose \theta에 위치한 물체의 j 번째 keypoint의 카메라 프레임 좌표를 나타냅니다. 이때 offset 방식, vector 방식, 마지막으로 저자가 제안한 radial 방식이 있습니다.

offset 방식에서는 regression된 quantity인 m_o는 두 3D point 사이의 변위를 의미하고 m_o=(\Delta x, \Delta y, \Delta z)=(x_i-x_j, y_i-y_j, z_i-z_j)로 표현합니다.

vector 방식에서는 3D quantity인 m_v는 p_i에서 k^\theta_j를 가리키는 unit vector로 표현하게 되는데 m_v=(dx, dy, dz)=\frac{m_o}{||{m_o}||} 로 표현할 수 있습니다. 이때 3D vector 방식은 m_p=(\phi, \psi)=(\cos^{-1}dz, \tan^{-1}\frac{dy}{dx})로 표현하여 2D 극좌표 방식으로 대체하여 파라미터로도 사용할 수 있습니다.

저자가 제안한 radial 방식의 1D quantity인 m_r은 단순하게 점 사이의 Euclidean distance 입니다. 식으로 표현하면 m_r=||m_o|| 입니다.

자세한 설명이 좀 길었습니다. 방금 언급된 quantity 들은 p_i와 k^\theta_j의 관계에 대한 다양한 정보를 encoding 함을 의미하는데, 여기서 저희가 중점적으로 봐야 하는 의미는 m_v, m_p, m_r은 직접적으로 m_o를 유도를 할 수 있지만 m_o를 다른 파라미터로부터 도출을 할 수가 없다는 사실이 하나가 있고 m_r과 m_v, m_p는 서로 독립적이므로 이러한 geometric information의 차이는 서로 다른 차원을 의미하게 되므로 이로 인해 radial voting의 정확도가 높아지는 이유가 됩니다.

3.2 Keypoint Estimation Pipeline

앞서 설명한 voting 방식은 keypoint estimation pipeline 내에서 상호교환적으로 사용할 수 있다고 합니다.

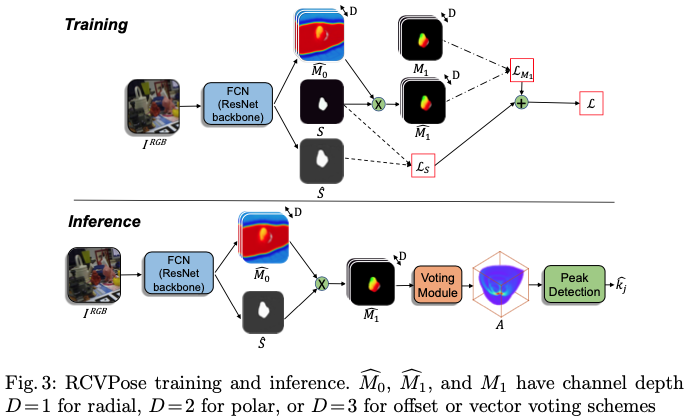
그림3은 학습과 예측을 하는 전체적인 과정을 나타낸 그림입니다. 학습 과정을 살펴보면 RGB 이미지 I^{\\RGB}, pose \theta에서 foreground 물체의 GT를 binary segmentation한 S, GT keypoint 좌표 k^\theta_j, matrix M_1로 표현한 S의 각 픽셀에 대한 GT voting 방식 값은 m_o, m_v, m_p, m_r 중 하나입니다. M_1은 voting 방식 값 중 하나를 사용하여 주어진 k^\theta_j에 대해 계산되고 채널의 depth를 의미하는 D가 m_o, m_v의 경우 D=3, m_p의 경우 D=2, m_r의 경우 D=1이 됩니다. Loss \mathcal L을 계산하기 위해 S와 M_1을 모두 평가합니다.

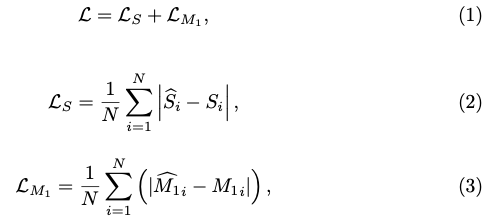
모든 N개의 픽셀에 대해 \mathcal L을 계산하고 네트워크의 출력은 S의 추정치인 \hat S와 M_1의 추정치인 unsegmented \hat {M_1} 입니다.

계속해서 그림3에 해당하는 inference 과정을 보겠습니다. I^{\\RGB}가 입력으로 들어갈 때 추정된 \hat S와 \hat M_0를 반환하고 element-wise multiplication을 통해 segmentation 된 추정치 \hat M_1을 얻을 수 있습니다. \hat M_1의 각 픽셀 (u_i, v_i)은 I의 depth field인 I^D에서 해당 3D 좌표 (x_i, y_i, z_i)를 얻고 다음 voting module을 통해 초기에 비어 있는 3D accumulator space인 A에 독립적으로 투표를 하는 진행합니다.

voting은 각 voting 방식에 대해 각각 수행되며 voting 방식 별로 구분됩니다.

offset voting에서는 accumulator space A에 해당하는 bin은 커지면서 keypoint k^\theta_j를 포함하는 A(x_i+\hat M[u_i, v_i, 0], y_i+\hat M[u_i, v_i, 1], z_i+\hat M[u_i, v_i, 2])의 특정 bin에 voting 합니다.

vector, ploar voting에서는 곡선 \alpha(x_i+\hat M[u_i, v_i, 0], y_i+\hat M[u_i, v_i, 1], z_i+\hat M[u_i, v_i, 2])가 있을 때 \alpha>0인 경우 해당 곡선에 교차하는 모든 A의 bin이 증가하여 (x_i, y_i, z_i) 및 k^\theta_j와 교차하는 곡선을 따라 모든 bin에 투표를 진행합니다.

radial voting에서는 (x_i, y_i, z_i)를 중심으로 radius \hat M_1[u_i, v_i]의 구와 교차하는 모든 A의 bin들이 증가하면서 k^\theta_j가 있는 구의 표면에 위치한 모든 bin에 대해 투표를 진행합니다.

위 세 가지 voting 방식 중 어떤 방식을 사용하든 모든 (u_i, v_i)에 대한 voting이 끝나면 k^\theta_j를 포함하는 A의 bin에 global peak가 존재하게 됩니다. 간단한 peak detection operation으로 keypoint의 위치를 \hat k^\theta_j을 A의 precision 내에서 추정하는 것으로 충분하다고 합니다. 최종적으로는 실험을 통해 radial voting 방식이 다른 방식들보다 keypoint estimation에 대한 정확도가 가장 좋았다고 합니다.

3.3. RCVPose

위의 keypoint voting 방식이 결국 제안된 RCVPose의 핵심이라고 볼 수 있습니다. 앞서 얘기했듯이 radial voting 방식이 가장 성능이 좋았고 그림 3에서 알 수 있듯이 FCN-Resnet module되어 있는 것을 볼 수 있습니다. 논문에서는 backbone으로 ResNet-152를 사용했다고 합니다. 각 물체의 bounding box의 corner에 선택되는 keypoint의 개수는 최소 3개로 선택되도록 설정을 하였습니다. keypoint는 각 물체의 표면뿐만 아니라 중심으로 부터 두 개의 물체 radius uint(반경 단위)까지 배치될 수 있게 스케일링 되었다고 합니다.

모든 voxel은 초기값이 0으로 되어있으며 voting이 진행됨에 따라 값이 증가하도록 설정하였습니다. voting 과정은 3D sphere rendering과 유사하고 sphere surface와 교차하는 voxel의 값은 증가하게 됩니다. 해당 과정은 Andre’s circle redering algorithm을 기반으로 한다고 합니다. z축의 양방향에서 구의 중심으로부터 구 반경 내에 속하는 xy평면에 평행하는 2D 평면 공간인 A를 생성합니다. 각 평면에 대해 구와 해당 평면과 교차하여 형성된 원의 반지름이 계산되고 이렇게 계산된 모든 voxel은 해당 원과 교차하는 만큼 증가하게 됩니다. 이러한 과정은 정확하면서 효율적인데 효율적인 이유는 각 sphere rendering에 대해 voxel의 일부만 사용하면 되기 때문입니다. 이러한 과정은 반복적인 PnP알고리즘을 사용하는 방법보다는 훨씬 효율적이라고 저자는 주장합니다.

4. Experiments

실험은 LINEMOD, Occlusion LINEMOD, YCB-Video에서 진행하였습니다.

Comparison with SOTA

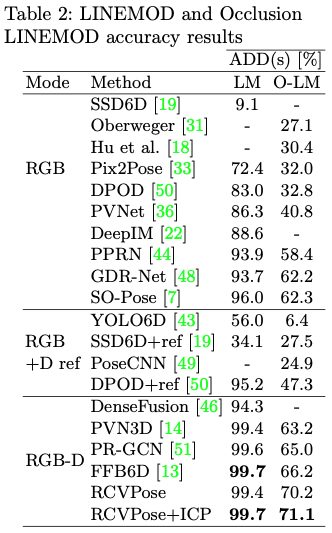
Occlusion LINEMOD에서도 성능이 향상된 것을 볼 수 있습니다. RCVPose의 강점 중 하나는 scale에 대한 내성이라고 합니다. 물체가 작아질수록 성능이 저하되는 대부분의 방법들과 달리 크게 영향을 받지 않았다고 합니다. ape, cat의 경우 정확도가 크게 오른 것을 확인했다는데 해당 정량적 평가를 다룬 표는 appendix 페이지에도 없네요.

그림5는 또 다른 강점을 시각화한 그림입니다. 각 픽셀에 대해 독립적으로 voting을 누적하기 때문에 부분적인 occlusion에 강인하고 최대 70%의 occlusion을 겪는 물체도 인식하는 것을 확인하였습니다.

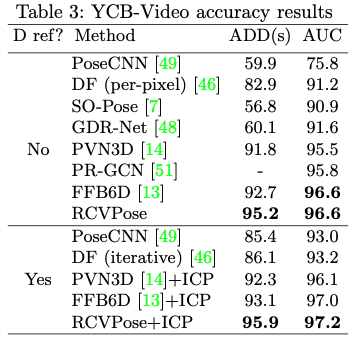
YCB-Video의 결과를 다룬 표입니다. 다른 방법론들과 비교해봤을 때 SOTA를 달성한 것을 확인할 수 있습니다. BOP 챌린지 당시 FFB6D보다 성능을 향상시켰다고 합니다. 이때 YCB-Video에서 추가적으로 사용되는 평가 지표인 AUC는 ADD(s) 값을 적용하여 transformation estimation의 성공 여부를 결정하고 해당 결과를0~100mm 내의 threshold에 걸쳐 합산을 한 결과라고 보시면 될 것 같습니다.

5. Conclusion

ResNe-based radial estimator와 새로운 keypoint voting 방식을 결합한 hybrid 6D pose estimator RCVPose를 제안하였습니다. radial voting 방식은 특히 keypoint가 더 disperse되어 있는 경우 더 정확한 것으로 나타났는데 이는 3개의 keypoint만 있으면 더 정확한 estimation이 가능하기 때문입니다. 6D pose estimation의 대표적인 데이터셋 3개에서 SOTA를 달성했으며 BOP 벤치마크에서 Occlusion LINEMOD에서 18FPS의 속도로 높은 순위를 달성하였습니다.