세 번째 x-review입니다. 이번에는 지난 NetVLAD 리뷰에 이어 Patch-NetVLAD를 들고 왔습니다. . 😏

Introduction

Visual Place Recognition(VPR)은 robotics와 autonomous system의 중요한 전제 조건입니다. 예를 들자면, SLAM 시스템에서 이전에 방문한 장소를 인식하고, 위치를 추정하는 기술로 사용될 수 있겠죠.

이 VPR은 일반적으로 query image가 주어졌을 때, database image 내에서 가장 유사한 이미지를 검색하는 image retrieval task로 구성됩니다. 보편적으로 query image와 reference image를 표현하는 방식에는 global descriptor를 사용하는 것과 local descriptor를 사용하는 것이 있습니다.

global descriptor를 사용하는 경우에는, 이미지의 전체적인 특징을 고려하기 때문에 appearance와 illumination의 변화에 강인합니다. Global descriptor는 이미지를 대표하는 하나의 vector로 표현되기 때문에 image의 전체적인 특징을 잘 요약할 수 있습니다. 반면에 local descriptor는 픽셀 단위의 작은 영역에 집중하여 이미지의 지역적인 특징을 추출합니다. 이는 정확한 6-DoF pose estimation과 같은 작업에 용이한데, 그 이유로는 작은 영역에 집중하여 특징을 추출하므로 이미지의 지역적인 변화나 변형에 민감하게 반응할 수 있기 때문에 image의 작은 부분의 상대적인 위치나 방향을 추정하는데 도움이 되기 때문입니다.

저자는 이런 local descriptor와 global descriptor 각각의 장점을 합치면서, 단점을 줄인Patch-NetVLAD system을 제안합니다. Patch-NetVLAD가 제안되기 전만 해도 local descriptor와 global descriptor 각각의 장점을 고려하여 결합했던 연구가 많지 않았다고 하네요. 😮

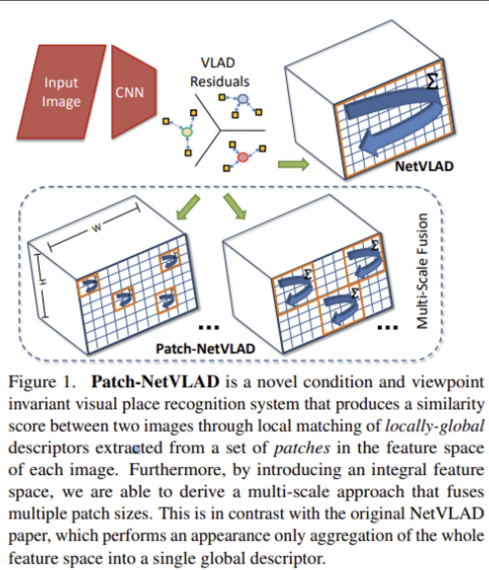
본 논문의 contribution은 다음과 같습니다.

1. locallly-global descriptor를 사용하여 image pair 간의 similarity score를 생성하는 새로운 place recognition system 도입
2. single scale만 가져가는 것보다 높은 성능을 내기 위해 서로 다른 크기의 hybrid descriptor를 결합하는 multi-scale fusion 제안 (연산량을 줄이기 위해 integral feature space 개발)
3. 성능과 속도 면에서 SOTA 달성

Methodology

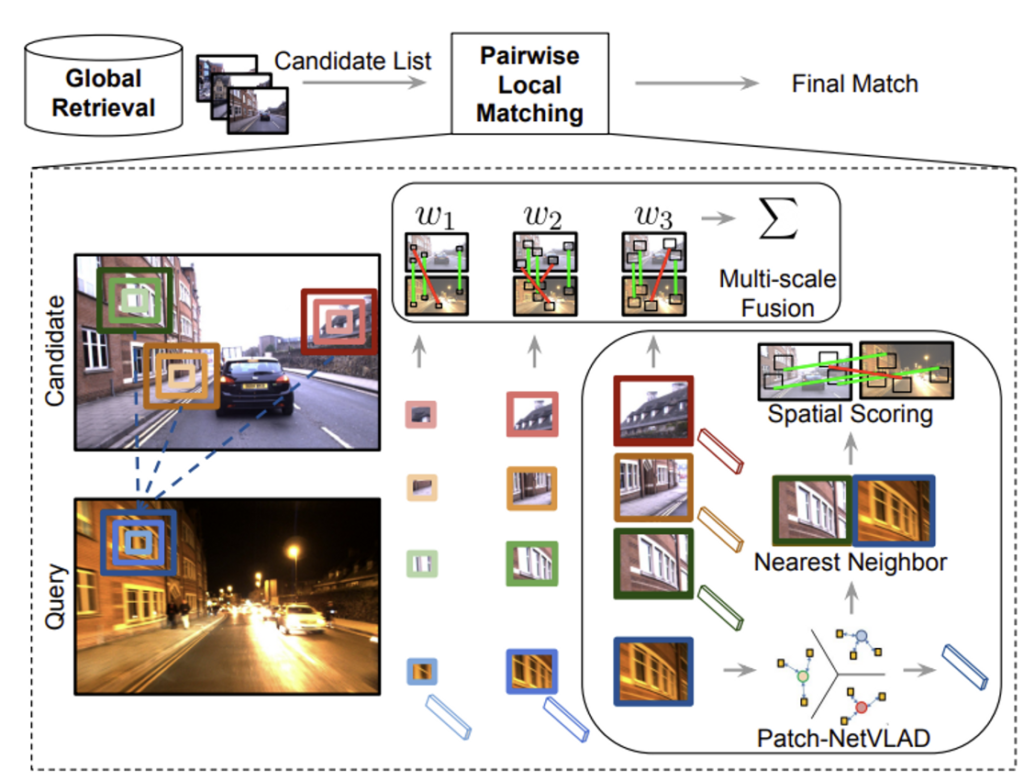
전체 파이프라인은 위 그림과 같습니다.

먼저 기존 NetVLAD descriptor를 사용하여 query image에 대해 가장 유사한 이미지들인 top-k개(본 논문에서는 k=100을 사용)의 match를 뽑게 됩니다. 그 다음 Patch descriptor를 계산하게 되고, 이 patch level의 descriptor를 local matching하여 앞서 뽑아두었던 match list를 재정렬(Reranking)함으로써 최종적으로 image retrieval이 끝납니다.

그림에서 상단 부분인 Global Retrieval을 통해 나온 Candidate List → Pariwise Local Matching → Final Match 부분을 간략하게 설명한 것인데, Pairwise Local Matching 과정의 Multi-scale Fusion이나 Nearest Neighbor, Spatial Scoring 부분은 아래에서 다뤄보도록 하겠습니다.

Original NetVLAD Architecture

그 전에 잠깐 original NetVLAD에 대해 잠깐 살펴보고 가겠습니다.

NetVLAD는 VLAD에서 착안된 방법론으로 CNN model로부터 추출된 intermediate feature map을 사용하여 image를 representation하며, 이 feature map을 aggregate하여 하나의 embedding을 생성합니다.

Image I가 주어지면, CNN을 통과해서 나온 중간 feature map size는 H x W x D 차원이 됩니다. 이 D차원의 feature들을 K개의 cluster center과의 residual을 계산하여 aggregate하게 되는데, 이 때 residual을 soft assignment를 사용하여 가중치를 할당하고, 이 weight를 사용해서 feature들을 합한 K x D 차원의 행렬을 생성합니다. 이 K x D 차원의 행렬이 이미지의 global descriptor로 사용되는 것이지요.

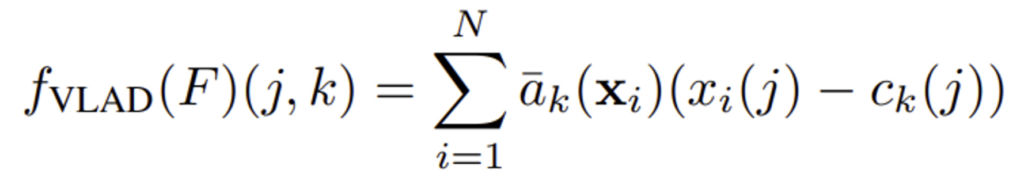
• x_{i}(j) : i번째 descriptor의 j번째 element
• a_{k} : soft assignment
• c_{k} : k번째 cluster center

NetVLAD에 대해 보충 설명은 제 지난 X-review를 참고하면 될 것 같습니다 . . .

아무튼 이 기존 NetVLAD 방식은 N = H x W로 설정하여, feature map 내의 모든 descriptor를 aggregate하여 global image descriptor를 생성한다고 하였습니다만, , , Patch-NetVLAD는 N << H x W로 두어 local patch에 대한 descriptor를 추출합니다.

결국 query/reference image pair 간에 multi scale로 이러한 patch들을 cross-matching하게 되며, 최종 image retrieval에 사용할 similarity score 즉 유사도 점수를 계산해 내는 것입니다.

Patch-level Global Features

Patch 단위로 global descriptor를 추출하는 방식에 대해 알아봅시다.

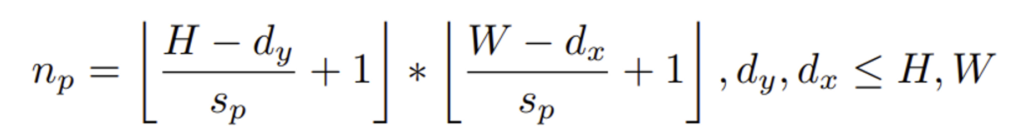
• n_{p} : 총 Patch의 개수
• s_{p} : stride
• d_{x}, d_{y} : patch 크기

본 논문에서는 Feature map F ∈ \mathbb{R}^{H×W×D}에서 d_{x} x d_{y} 크기의 patch 집합 {P_{i}, x_{i}, y_{i}}^{n_p}_{i=1}를 s_{p} (stride) 간격으로 dense하게 추출하며, 이때 총 Patch의 개수는 위 식으로 정해지게 됩니다.

x_{i}, y_{i}는 patch의 중심 좌표를 의미하며, 추출한 patch는P_{i} ∈ \mathbb{R}^{(d_x * d_y) * D}으로 표현할 수 있겠습니다. 실험 결과에 따르면, 정사각형 patch가 다양한 환경에서 가장 일반화된 성능을 제공했다고 하네요, 하지만 수직이나 수평 방향의 다른 texture 주파수를 가진 경우 같은 특정 상황에서는 다른 패치 형태를 고려해볼 수도 있습니다.

기존의 local feature-based maching기법들이 image내에서 비교적 작은 영역에 대해 feature를 추출하는 것에 비해 patch feature는 보다 더 넓은 영역을 커버함으로써 semantic한 정보를 암시적으로 포함할 수 있게 됩니다.

이제 파이프라인의 나머지 부분인, patch descriptor의 mutual nearest neighbor matching과, spatial scoring을 아래서 설명하도록 하겠습니다.

Mutual Nearest Neighbors

각 patch로부터 descriptor를 추출하면 patch descriptor 집합 {f_{i}}^{n_p}_{i=1}이 생성됩니다. 여기서 f_{i}는 NetVLAD aggregation과 projection layer를 통과한 descriptor를 의미합니다. (projection layer란 NetVLAD 과정에서 intra normalization, L2 normalization을 적용하는 layer 입니다.)

이제 query image와 database내의 image를 비교하여 유사한 descriptor 쌍을 얻기 위해 mutual nearest neighbor matching 과정을 거칩니다.

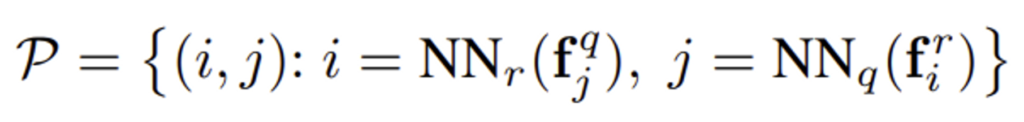
• NN_q(f) = argmin_j ||f – f^q_j||_2
• NN_r(f) = argmin_j ||f – f^r_j||_2

위는 각각의 reference patch를 기준으로 가장 가까운 query의 patch descriptor와NN_r(f^q_j), query patch를 기준으로 가장 가까운 reference patch descriptorNN_q(f^r_j)를 찾아 matching한 patch pair set을 나타냅니다.

이렇게 matching된 patch set가 주어지게 되면 이제 image retrieval에 사용되는 spatial matching score를 계산할 수 있겠죠.

Spatial Scoring

이제 mutual nearest neighbor matching과정을 거쳐 나온 patch image pair간의 유사도를 계산하는 과정입니다. 저자는 RANSAC-based scoring method와, spatial scoring method를 제안했습니다.

RANSAC Scoring

RANSAC 방식을 통한 score은 mutual nearest neighbor matching단계를 거쳐 계산된 patch를 사용하여 두 이미지 사이의 2D homography를 구하고 여기서 나오는 inlier의 수로 계산됩니다. 즉, RANSAC 알고리즘을 사용하여 추정된 homography model의 일치하는 patch 수를 계산하는 것인데, 일치하는 patch 수가 많을수록 두 이미지가 더 유사하다고 판단할 수 있겠습니다.

이 방식은 더 높은 retrieval 성능을 위해 많은 시간이 소요됩니다. inlier에 대한 오차 허용 범위는 s_p(stride)로 설정하였으며, 계산한 score은 patch의 수로 normalize함으로써 multiple scale에서의 score 결합 시 relevant하게 작용되게 하였습니다.

Rapid Spatial Scoring

앞에서 RANSAC 기반 score 계산 시에는 시간이 많이 걸린다고 했습니다. 저자는 이에 대안으로 rapid spatial scoring을 제안하였는데, 이는 sampling 과정 없이 직접 매칭된 feature pair에 대해 score를 계산함으로써 시간을 크게 줄일 수 있습니다.

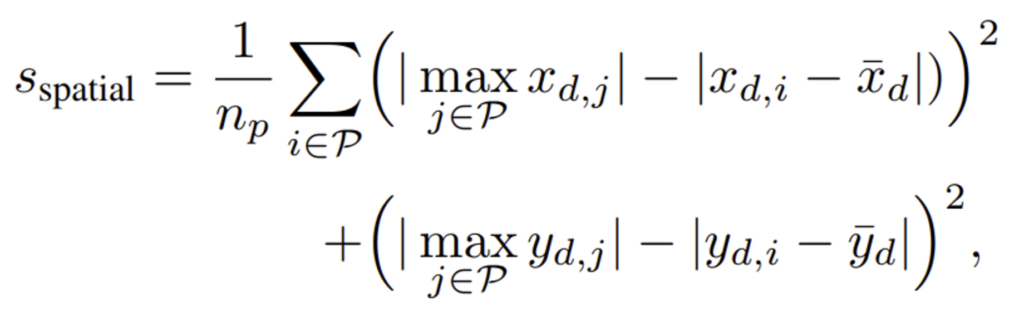
• x_d = {x^r_i – x^q_j}_{(i, j)∈P} : matching된 patch들 간의 수평 방향 변위
• y_d : matching된 patch들 간의 수직 방향 변위
• \bar{x}_d = {1 \over |x_d|}∑_{x_{d,i}∈x_d} x_{d,i} : x_d의 평균 변위
• \bar{y}_d : y_d의 평균 변위

수식은 위와 같습니다. |x_{d,i} - \bar{x}_d|와 |y_{d,i} - \bar{y}_d|는 각각 변위의 평균값으로부터의 잔차를 나타내고 있습니다. 결국 patch들의 위치 변화가 평균 변위와 비교하였을 때 얼마나 일관성이 있는지 측정하는 것입니다. score가 낮을수록 patch들의 위치 변화가 일치하지 않는 것을 의미하며, score가 높을수록 위치 변화의 일관성이 높다는 것을 의미하겠죠 .

Multiple Patch Sizes

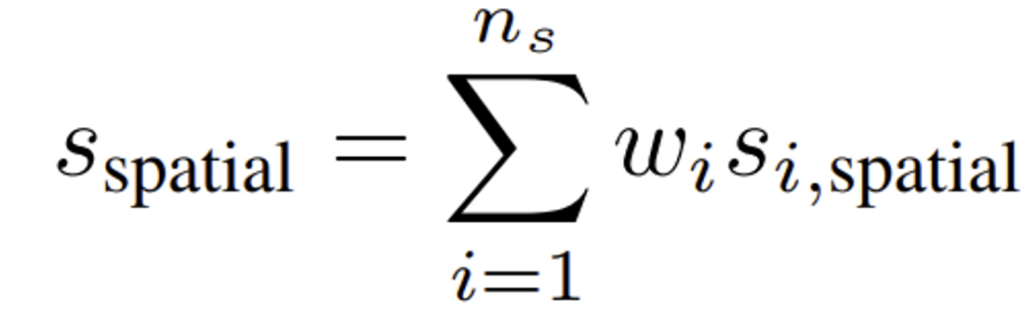
• w_i : i번째 patch 크기 score에 할당된 가중치
• s_i : i 번째 patch 크기에 대한 score
• n_s : patch size

이제 다양한 patch size에 대한 최종 Score입니다. 위 수식은 n_s개의 다른 패치 크기에 대해 spatial matching score를 계산한 후, 이 score들의 가중 평균을 최종 score로 사용한다는 것을 보여주네요. 여기서 weight는 각 score에 부여된 중요도를 나타냅니다. weight의 합은 1이며, 각 가중치는 0보다 큰 값을 가지게 됩니다.

IntegralVLAD

저자는 다양한 크기의 patch를 효율적으로 처리하기 위해 IntegralVLAD를 제안하였습니다. 이 IntegralVLAD는 Integral Image 개념을 도입한 것인데, Integral Image란 이미지의 특정 위치까지의 픽셀 값을 누적하여 저장한 이미지를 의미합니다.

추출된 patch의 descriptor는 1×1 크기의 patch descriptor들의 합으로 계산할 수 있습니다. 이를 이용해서 사전에 integral patch feature map을 미리 계산할 수 있는 것이죠. integral feature map은 아래와 같이 표현됩니다.

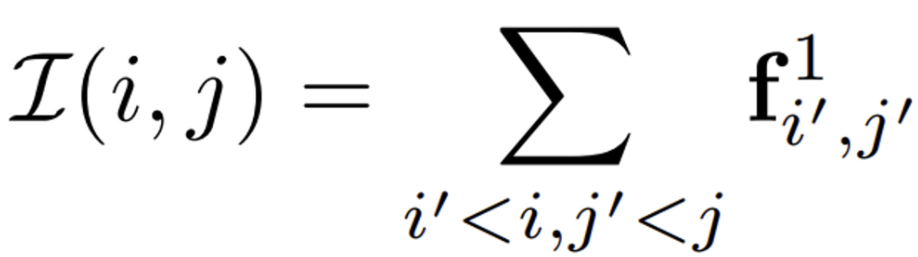
• f^1_{i’,j’} : 1 크기의 patch에 대한 VLAD aggregate된 patch descriptor

이렇게 생성된 integral feature map I 내에서 네 개의 위치를 사용함으로써 임의의 scale에 대한 patch feature를 복원할 수 있습니다. 이 네 위치는 아래의 kernel을 사용하여 선택할 수 있습니다.

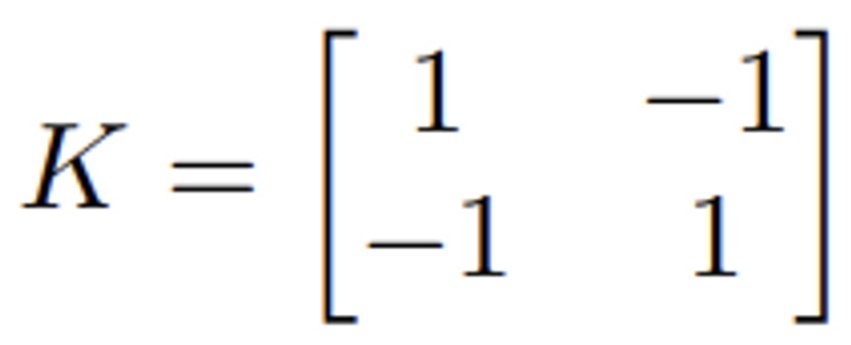
K를 통해 구한 4개의 reference 위치를 이용하여 2D depth-wise dilated convolution을 수행하면, 해당 위치에서 patch의 feature를 추출해 낼 수 있습니다. dilation은 커널 내에서의 간격을 조절하는 역할을 수행하며, 이를 통해 patch 크기와 동일한 영역을 고려할 수 있다고 합니다.

결국 IntegralVLAD는 scale에 대한 patch feature들을 복원하는데 사용되며, 이를 통해 multi scale에서의 patch feature들을 효과적으로 계산할 수 있게 되는 것입니다.

Experiment

실험 결과 [Table1]을 보면, 기존에 좋은 성능을 내던 global descriptor method인 NetVLAD, DenseVLAD, AP-GEM과 Patch-NetVLAD의 성능을 볼 수 있습니다. Patch-NetVLAD가 각각의 방법론마다 평균 17.5%, 14.%, 22.3%(R@1에 대해) 정도 더 좋은 성능을 내고 있네요. 이러한 성능 차이는 특히 dataset내에서 appearance 변화가 클 때 두드러지는데, 예를 들어 Nordland dataset에서 Patch-NetVLAD와 original NetVLAD의 차이가 34.5% 나는 것을 볼 수 있습니다.

Patch-NetVLAD와 SuperGlue를 비교해보자면, , pittsburgh 30k, Tokyo 24/7 dataset에 대해서는 SuperGlue가 더 성능이 좋네요.

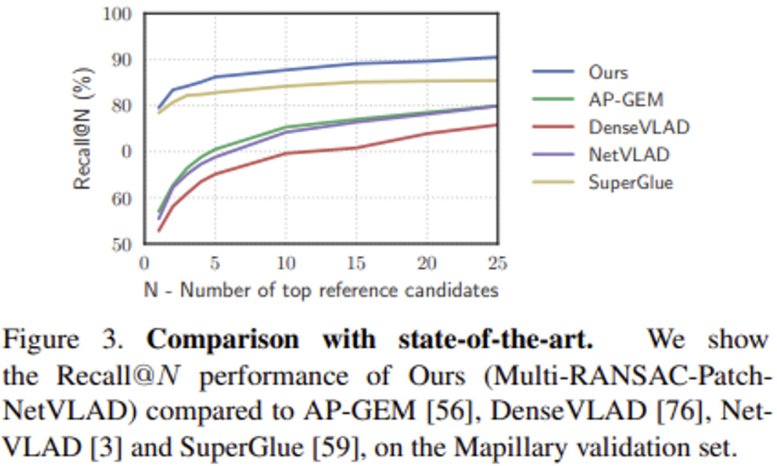
[Figure 3]을 보면, Mapillary dataset에 대해 Recall@N 성능을 비교한 것인데, Patch-NetVLAD와 SuperGlue의 R@1에서의 성능 차이는 1.1%이지만, R@25에서는 5.1%의 차이를 보이고 있습니다.

Ablation Studies

Single-scale and Spatial Scoring

1. multi-scale fusion 대신 sigle patch size + RANSAC를 사용한 것과 2) single patch size + rapid spatial method를 사용한 것과 3) multi scale fusion에 rapid spatial method를 사용한 것과 4) multi-fusion approach( Multi-RANSAC-Patch-NetVLAD)를 비교한 결과 Multi-RANSAC이 가장 좋은 성능을 보입니다.

Patch Descriptor Dimension

위 그림을 보면, 차원이 낮고 single patch를 사용할수록 성능은 좀 떨어지지만 속도가 아주 빠른 것을 볼 수 있습니다. 또 Multi-RANSAC-Patch-NetVLAD(dim = 4096) (빨간색 별)을 보면 SuperGlue보다 좀 더 빠르지만 성능이 더 좋습니다.

마지막으로 정성적 결과입니다.

NetVLAD와 SuperGlue는 모두 잘못된 matching을 했지만, Patch-NetVLAD는 맞는 reference image를 잘 retrieval 한 결과를 가져왔는데요, Tokyo 24/7 dataset에서 가져온 저 이미지는 낮과 밤으로 시간도 다르고, viewpoint도 심하게 이동되었으며, occlusion도 있기에 어려운 image인데 잘 검색한 결과를 보이고 있습니다 .