Yet Another Review of Transformer (Attention Is All You Need, NIPS 2017)

안녕하세요. 백지오입니다.

다섯 번째 X-REVIEW는 Transfomer를 준비하였습니다. 다만 Attention Is All You Need 논문의 리뷰보다는 Transformer 모델에 대해 온갖 자료를 뒤져보며, 상세한 튜토리얼을 작성하는 느낌으로 작성하여 논문 리뷰 형식으로 작성하지는 않았으니 양해 부탁드립니다.

Transformer와 Attention의 파급력과 활용 분야는 굳이 설명하지 않아도 알고 계시리라 생각됩니다.
저도 솔직히 너무 어려워 보여서 나중에 하려고 미루고 있었는데, 제가 최근 관심을 갖는 분야인 Multi-Modal Embedding과 기초 교육 내용으로 배우고 있는 분야, 우리 연구실과 공동 연구를 진행하는 다른 연구실에서 산출된 기술 문서 등 Transformer가 등장하지 않는 곳이 없어 더 이상 미룰 수가 없었습니다.

때문에 지난 3주간 트랜스포머 공부를 진행하면서 가능한 쉽고 상세하게 최고의 튜토리얼을 만들어보자는 생각으로 준비한 글이니 즐겁게 읽어주시기 바랍니다. ☺

---

Concept

트랜스포머를 이해하기에 앞서 트랜스포머가 어떤 배경에서 등장하였고, 어떤 컨셉의 모델인지 살펴보자.

Brief Introduction to NLP back then…

자연어 데이터는 여러 개의 단어들로 구성되며, 이 단어들은 문장의 문맥(context)에 따라 다른 의미를 갖는다. 예를들어, “나는 내 가족들을 사랑해.”와 “나는 스스로를 사랑해.” 두 문장에서, <사랑해>라는 단어가 수식하는 대상과 의미가 상이하다.

	<사랑>의 의미	<사랑>의 대상
나는 내 가족들을 사랑해	가족애, 화합, 조화	가족
나는 스스로를 사랑해	자기애, 자존감, 긍지	나, 스스로

이러한 문맥을 파악하는 것은 자연어 처리를 비롯하여 많은 딥러닝 분야에서 중요한 도전 중 하나이다. 특히 최근의 딥러닝 연구는 직관적으로 보이는 현상만을 설명하는 분류, 인식에서 나아가 데이터에 내재된 의미를 파악해야 하는 action recognition, description 등 복잡한 방향으로 나아가고 있다.

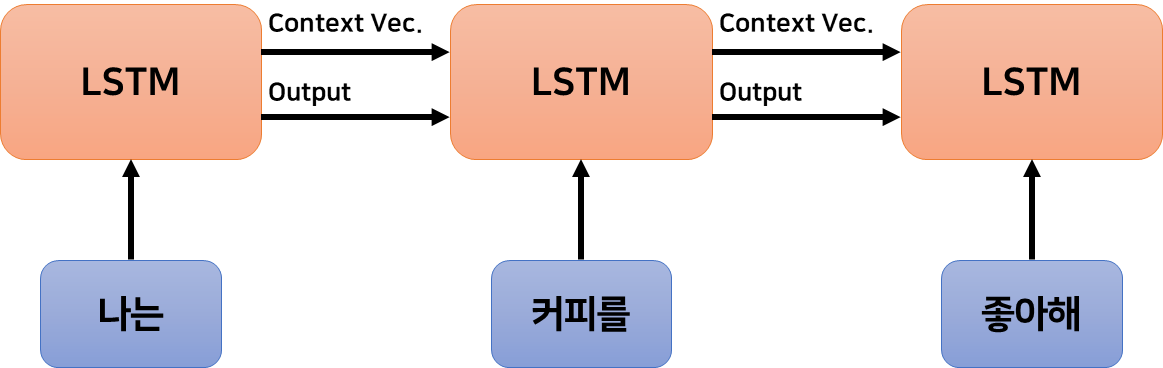
트랜스포머 이전의 자연어 처리 연구는 순환 신경망 구조를 활용하는 연구가 주류였다. 트랜스포머 이전의 SOTA 모델이자 RNN 기반 모델인 LSTM은 자연어 데이터를 단어 단위로 나누어 순차적으로 입력받는다. 각 단어가 입력될 때마다 문맥 벡터(context vector)에 문맥 정보를 신중하게 압축하여 저장한다.

이 과정을 비유하자면, 책의 내용을 작은 메모장에 메모하며 책을 읽는데 메모장이 모자라면 일부를 지우고 메모를 계속하며 읽은 후, 그 메모장을 보며 책에 대해 설명하는 것과 같다.

Concept of the Transformer

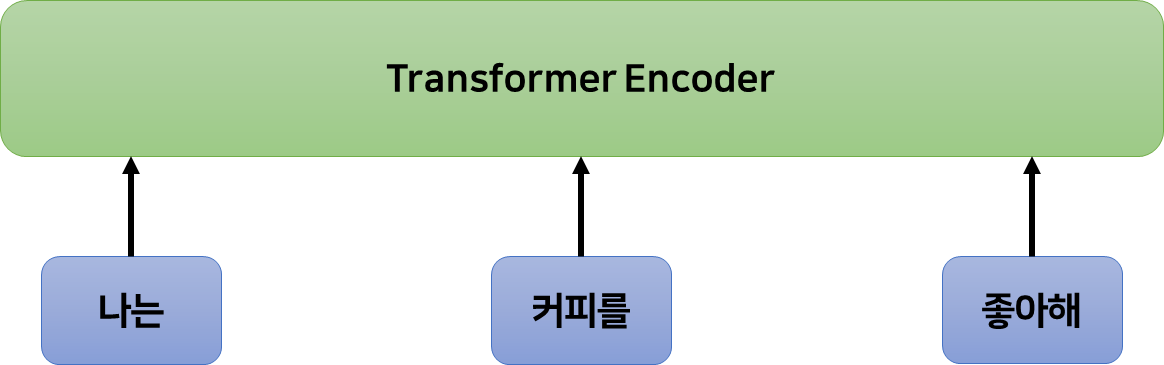
트랜스포머는 입력되는 데이터를 한번에 입력받는다. 그 다음, 어텐션이라고 하는 방법을 사용해 입력된 단어들이 각각 어떤 단어와 연관이 있는지, 데이터 전체에서 어떤 단어와 문장이 중요한지 등을 판단하여 이를 기반으로 한 벡터를 저장한다.

비유하자면 책 전체를 읽고 중요한 부분을 강조한 설명글을 작성한 후, 이 글을 보며 책에 대해 설명하는 것과 같다.

Structure

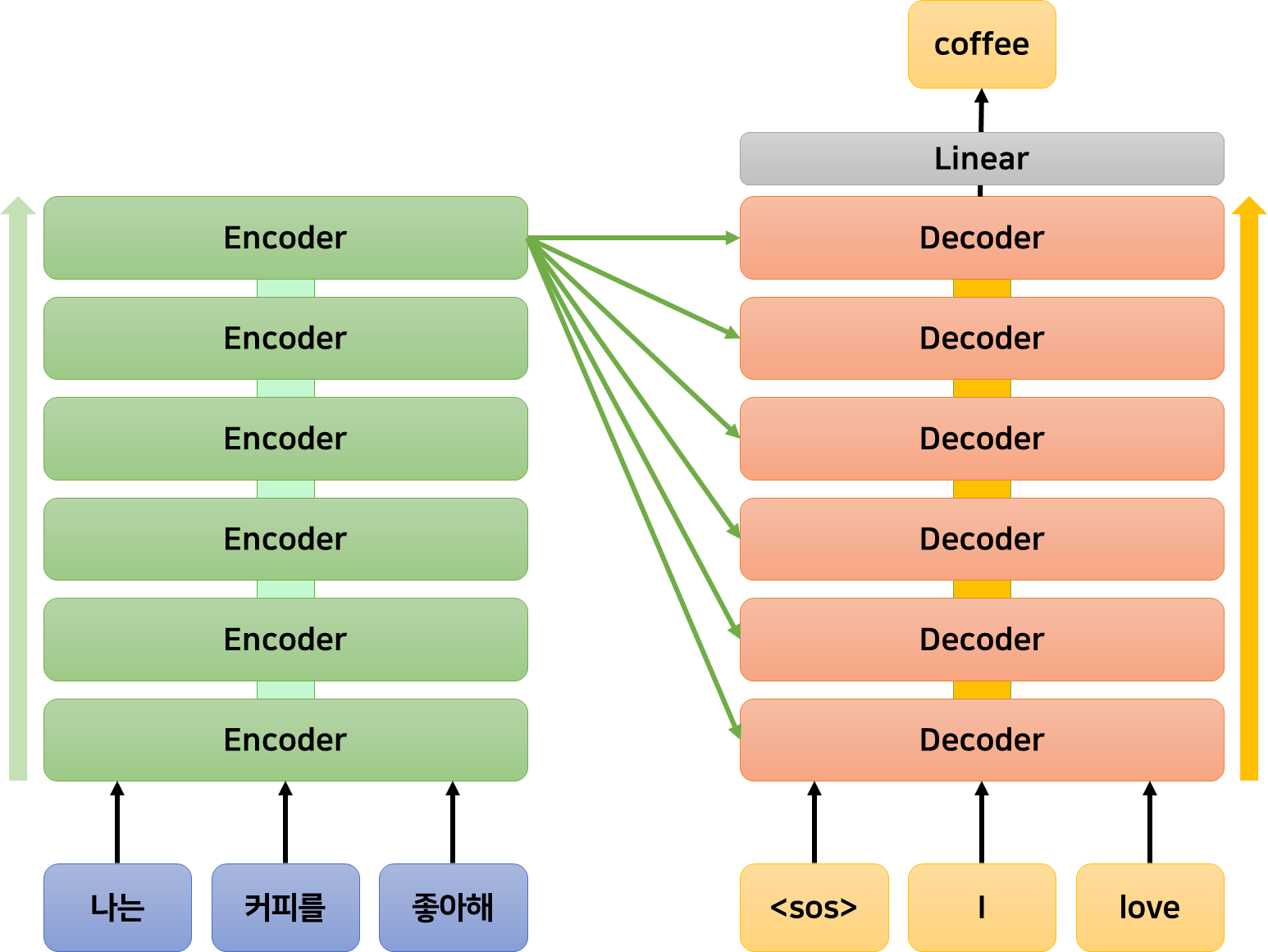
트랜스포머 모델은 입력 크기와 출력 크기가 모두 동일한 6개의 인코더와 6개의 디코더로 구성된다.

인코더는 주어진 데이터에 Self-Attention을 적용하여 데이터의 토큰들 사이의 관계를 판단하고, 이를 기반으로 데이터를 변형한다. 인코더의 입력과 출력 크기가 동일하기 때문에, 인코더의 출력은 다음 인코더의 입력으로 사용될 수 있다.

6개의 인코더를 거쳐 정제된 데이터는 이어서 6개의 디코더에 입력된다.
위 그림과 같이, 디코더는 인코더와 달리 이전 계층의 출력에 더불어 인코더의 마지막 출력을 입력으로 받는다.

디코더는 이전 계층의 출력에 Self-Attention을 적용하여 변형하고, 이를 쿼리 삼아 인코더의 마지막 출력에 대한 Cross Attention을 수행한다. 이는 인코딩 된 정보를 디코더가 원하는 형태로 서서히 변형하는 과정이다.

결과적으로 입력 데이터는 6개의 인코더로 인코딩 된 후, 6개의 디코더에 의해 원하는 대로 변형되어 출력된다.
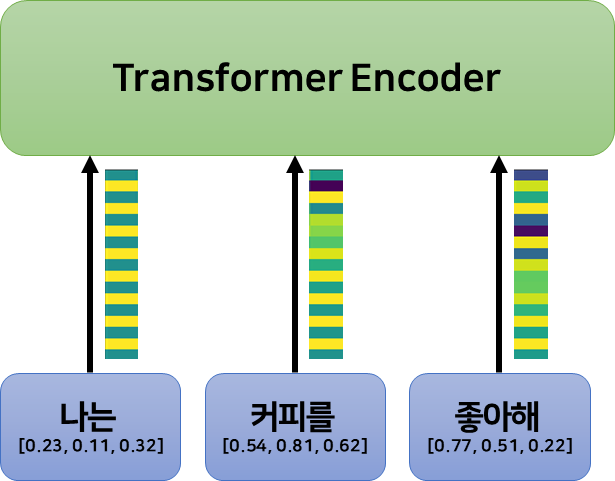
예를 들어 한국어를 영어로 번역하는 트랜스포머 모델은 “나는 커피를 좋아해”라는 문장을 인코더가 변형한 뒤, 이를 디코더가 “I love coffee”라는 형태로 변형하는 것이다.

---

Data Tokenizing & Embedding

트랜스포머에 데이터를 입력하기 위해서는 토큰화와 임베딩 과정을 거쳐야 한다. 이는 자연어 처리와 관련한 영역이므로 간단하게 설명하자면, 토큰화는 자연어를 어떠한 단위(여기서는 단어)로 나누는 것이고, 임베딩은 나누어진 토큰을 고정된 크기의 벡터로 변환하는 과정이다.

예를 들어, “나는 커피를 좋아해”는 [“나는”, “커피를”, “좋아해”]로 토큰화할 수 있으며, 각 토큰은 다시 어떤 임베딩 벡터 $e_i \in \mathbb{R}^E$ ($E$는 임베딩 벡터의 차원, 논문에서는 512이다.)로 변환되어, $[e_0, e_1, e_2]$와 같이 임베딩 된다.

단어의 임베딩은 각 단어가 유사한 의미를 가질 수록 가깝고, 유사하지 않은 의미를 가질수록 멀도록 수행되는데, 상세한 방법까지는 이 글에서 다루지 않겠다.

토큰화와 임베딩 과정을 거치면 $n$개의 단어로 구성된 자연어 데이터는 $n\times m$ 크기의 행렬로 변환된다.

Input Shape of Transformer

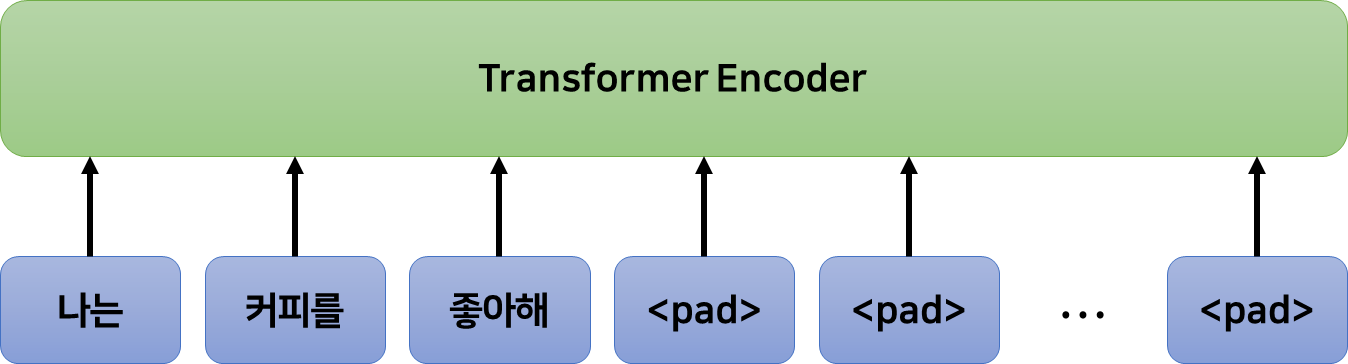
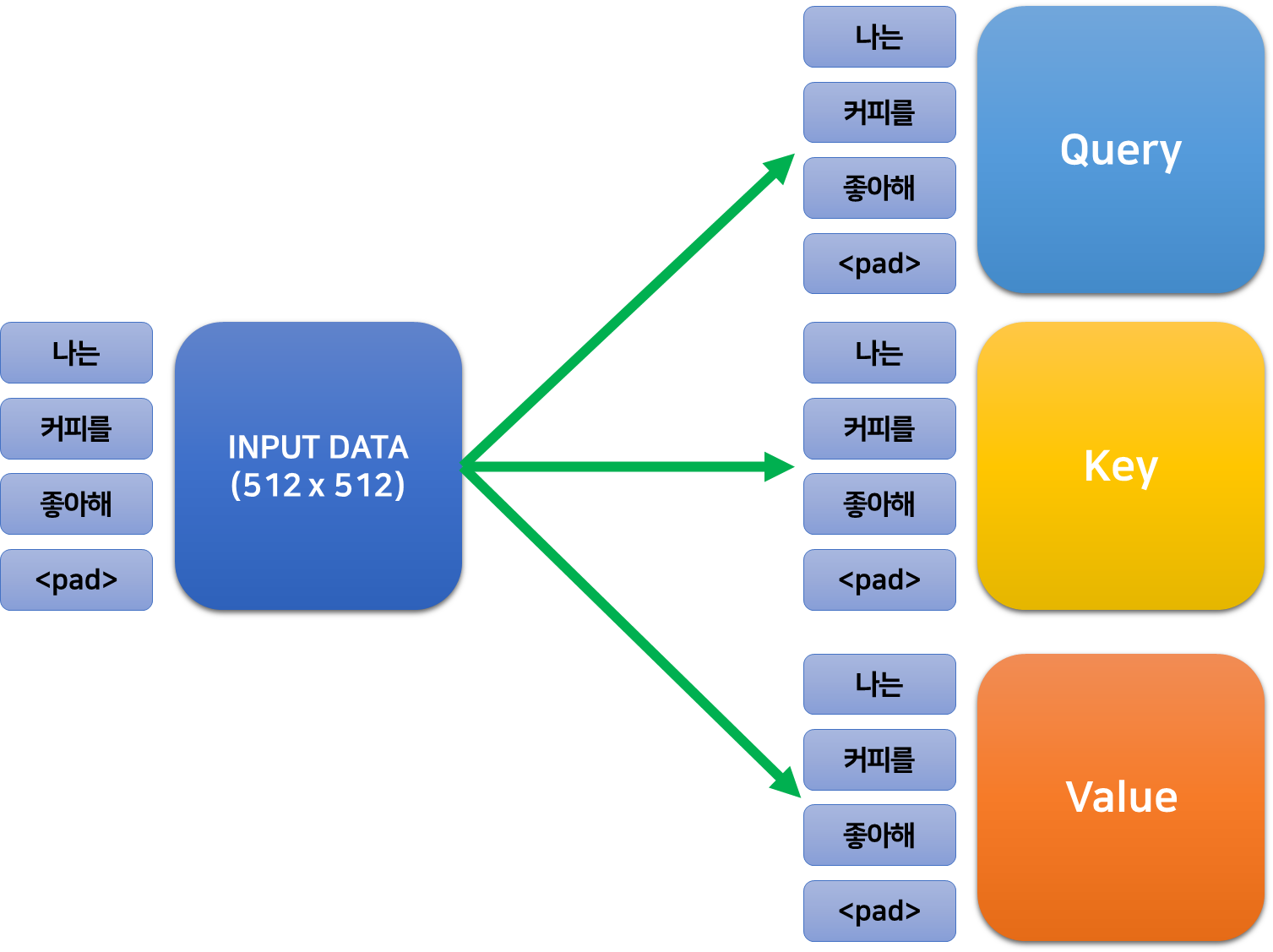
트랜스포머는 RNN 기반의 방법들과 달리 고정된 길이의 입력을 받는다. 논문에서는 최대 512개의 토큰을 입력으로 받기 때문에, 입력 데이터의 크기는 $512 \times m$이 된다.($m$은 임베딩의 크기) 입력하고자 하는 데이터가 512보다 작다면 남는 공간에는 <pad> 토큰을 넣고, 데이터가 512보다 크다면 분할하여 입력한다. (<pad> 토큰의 임베딩은 0이다.)

앞서 토큰화, 임베딩, 패딩을 모두 거친 트랜스포머의 입력 데이터 크기는 (트랜스포머의 입력 크기) $\times$ (단어 임베딩 크기 $E$) 즉, $512 \times 512$가 된다.

Positional Encoding

트랜스포머는 입력 데이터들을 순차적으로 받는 RNN 기반 방법들과 달리 한번에 모든 데이터를 입력받기 때문에 기본적으로 각 토큰들의 순서를 알 수 없다. 그러나 자연어에서 순서는 매우 중요한 의미가 있기 때문에 Positional Encoding을 통해 각 토큰에 순서 정보를 명시적으로 추가해준다.

Positional Encoding의 목적은 같은 단어라도 등장하는 위치에 따라 약간 다른 값(임베딩 벡터)을 갖도록 만드는 것이다.
이때 중요하게 고려해야 할 조건은 다음과 같다.

1. 위치 정보를 추가하는 것이 토큰의 임베딩을 약간 수정해야 한다.
   • 만약 위치 정보를 추가함에 따라 같은 단어의 뜻이 완전히 달라진다면, 모델은 단어의 뜻을 학습하지 못할 것이다.
2. Positional Encoding이 모든 위치에서 다른 값을 가져야 한다.
   • 만약 첫 번째 단어를 $1$이라는 값으로 인코딩하고, 열한 번째 단어도 $1$이라는 값으로 인코딩하면 첫번째 단어와 열한번째 단어가 같은 단어일 경우 완전히 같은 뜻으로 인코딩 될 것이다.
3. 가까운 단어들의 Positional Encoding은 유사해야 한다.
   • Positional Encoding의 목적 자체가 단어들의 상대적인 위치를 나타내는 것이기 때문에 가까운 단어들은 비슷한 값으로, 먼 단어들은 다른 값으로 인코딩 되는 것이 바람직하다.

<조건 1>에 따라, Positional Encoding은 임베딩 벡터에 작은 벡터를 더해주는 방식으로 수행된다. 만약 토큰의 임베딩 뒤에 순서를 나타내는 어떤 값을 concatenate 하게 되면 임베딩 벡터의 차원이 늘어나면서 비슷한 값을 가져야 할 임베딩 벡터들(유사한 의미를 갖는 단어들)이 먼 거리를 갖게 될 것이기 때문이다.

그렇다면 중요한 것은 “어떤 작은 벡터를 더해줄 것인가?”인데, 저자들은 삼각함수를 이용하여 positional encoding을 수행한다. 삼각함수는 $-1 ~ 1$을 반복하는 주기 함수이기 때문에, <조건 1>에서 요구하는 벡터를 약간 수정할 작은 값을 만드는 것에 적합하다.

그러나 주기함수는 어떤 값이 반복적으로 등장하기 때문에, <조건 2>를 불만족하지 않는가 싶은데, 저자들은 이를 두 개의 삼각함수를 함께 사용하여 해결한다. 어차피 입력의 크기는 $d_{model} = 512$개로 제한이 되어있기 때문에, 이 만큼의 다양성만 확보가 되면 되는 것이다. 또한, Positional Encoding은 어떤 스칼라값을 더하는 것이 아니라 벡터를 더하여 수행되기 때문에 한층 더 다양한 인코딩 값이 생성된다.

Positional Encoding을 위한 벡터 $PE_{(pos, 2i)}$는 다음과 같이 정의된다. ($pos$는 토큰의 위치, $i$는 임베딩 벡터의 $i$번째 값, $d_{model}$은 모델이 입력으로 받는 최대 길이를 의미한다.)

$$PE_{(pos, 2i)} = \sin(pos/10000^{2i/d_{model}})$$

$$PE_{(pos, 2i+1)} = \cos(pos/10000^{2i/d_{model}})$$

이를 시각화하면 아래 그림과 같다.

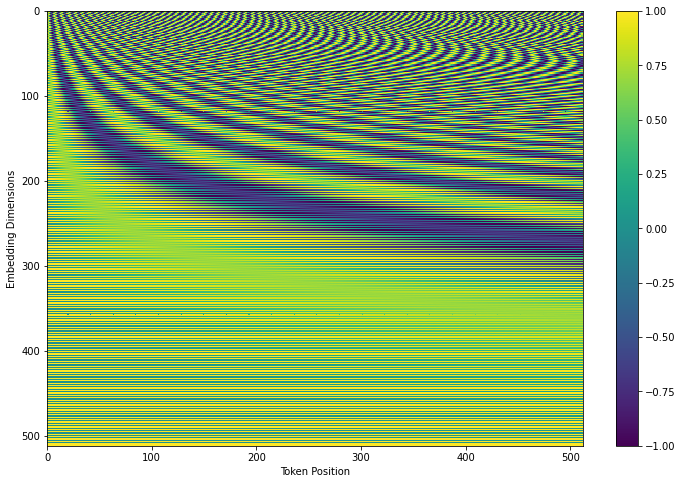
가로축이 토큰의 위치를 나타낸다. 즉, 0번째 단어는 위 그림에서 0번째 열에 해당하는 벡터를 더해준다.
위에서 볼 수 있듯이 모든 열의 벡터가 형태가 다르고, 거리가 먼 열일 수록 벡터의 형태도 더 달라진다.

PE를 생성하는 파이썬 코드는 아래와 같다.

Encoder

지금까지 (트랜스포머의 입력 크기) $\times$ (단어 임베딩 크기 $E$) 즉, $512 \times 512$의 크기를 갖는 입력 데이터를 얻었다. 이제 6개의 인코더를 거쳐 입력된 데이터를 어떠한 벡터로 만들어 줄 것인데, 이때 인코더는 모두 같은 크기의 입력과 출력을 갖는다. 즉, 인코더는 $512\times 512$ 크기의 입력을 받아 $512\times 512$ 크기의 값을 출력하고, 6개의 인코더를 거친 최종 출력 또한 $512\times 512$ 크기이다.

Multi-Head Self Attention

인코더는 가장 먼저 입력 데이터에 대하여 Multi-Head Self Attention을 수행한다. 우선 Multi-Head는 잠시 제쳐두고 Self Attention이 어떻게 이루어지는지 살펴보자. Self Attention은 그 이름처럼 주어진 입력 데이터에 내재된 정보들의 관계, 토큰과 토큰 사이의 유사성 같은 것들을 파악한다. 그 과정을 살펴보며 Attention이 정확히 어떻게 작동하는지, 원리를 살펴보자.

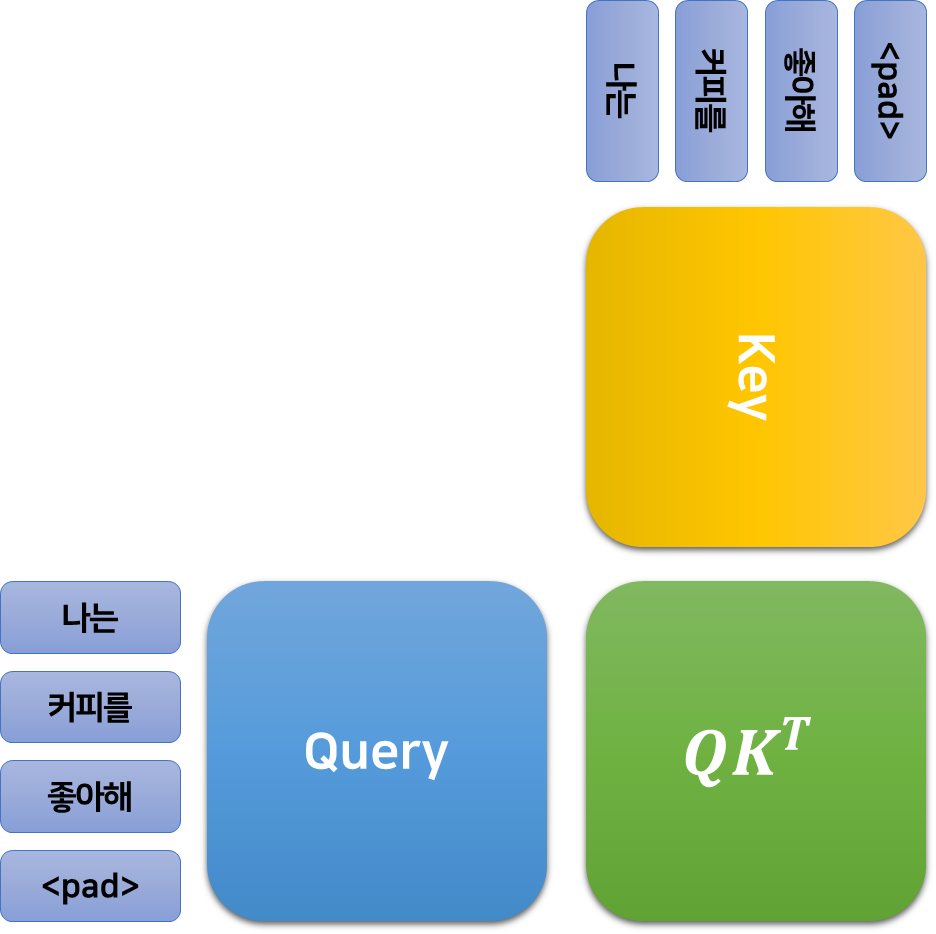
먼저 입력된 데이터를 세 개로 복사한 다음, 복제된 각각의 행렬에 어떤 (학습가능한) 가중치를 곱하여 세 개의 각기 다른 행렬로 만들어준다. 이때, 가중치는 $512\times 512$의 크기를 가지기 때문에 이렇게 얻은 세 가지 행렬 또한 인코더의 입/출력과 같은 크기를 갖는다.

이 행렬들을 각각 쿼리, 키, 벨류라고 한다.
이 행렬들 중 쿼리와 키를 내적 하고 스케일을 조정한 후, Softmax 함수를 적용하여 모든 값의 합이 1인 행렬로 만들고, 이 행렬을 다시 Value에 곱하여 데이터를 얻는다. 이를 Scaled Dot-Product Attention이라고 한다. 

$$ \text{Attention}(Q, K, V) = \text{softmax}(\frac{QK^T}{\sqrt{512}})V$$

$d_k$는 토큰의 임베딩 차원으로, 이 논문에서는 한 토큰을 512차원으로 임베딩하였으니 512이다.
이제 이 공식이 도대체 무엇을 의미하는지 살펴보자.

쿼리와 키

어텐션을 들여다보기에 앞서, 결국 쿼리, 키, 벨류 모두가 원본 데이터에 약간의 변환을 가하여 얻은 값에 불과함을 인지해야 한다. 쿼리, 키, 벨류의 각 행은 여전히 어떤 하나의 토큰에서 유도된 값이다.

쿼리와 키의 내적으로 얻어지는 $QK^T\in\mathbb{R}^{512\times 512}$ 행렬의 값 $w_{i, j}$는 $i$번째 단어의 쿼리 벡터와 $k$번째 단어의 키 벡터의 곱의 내적과 같다.

지금까지는 행렬의 $i$번째 행이 $i$번째 토큰에서 유도된 값이었으나, 이제 $i,j$번째 값은 $i$번째 토큰과 $j$번째 토큰에서 유도된, 각 토큰의 관계성을 포함한 값임에 주목하자.

이렇게 얻어진 행렬은 토큰의 임베딩 차원 $d_k$의 제곱근으로 나누어진 다음, Softmax 함수를 적용하여 행렬 속 모든 값의 합이 1이 되도록 조정된다. 이제 행렬 $QK^T$의 값 $w_{i, j}$는 전체 1 중에서 $i$번째 토큰과 $j$번째 토큰의 관계에 가져야 할 주목도(Attention)가 되었다.

어텐션의 적용

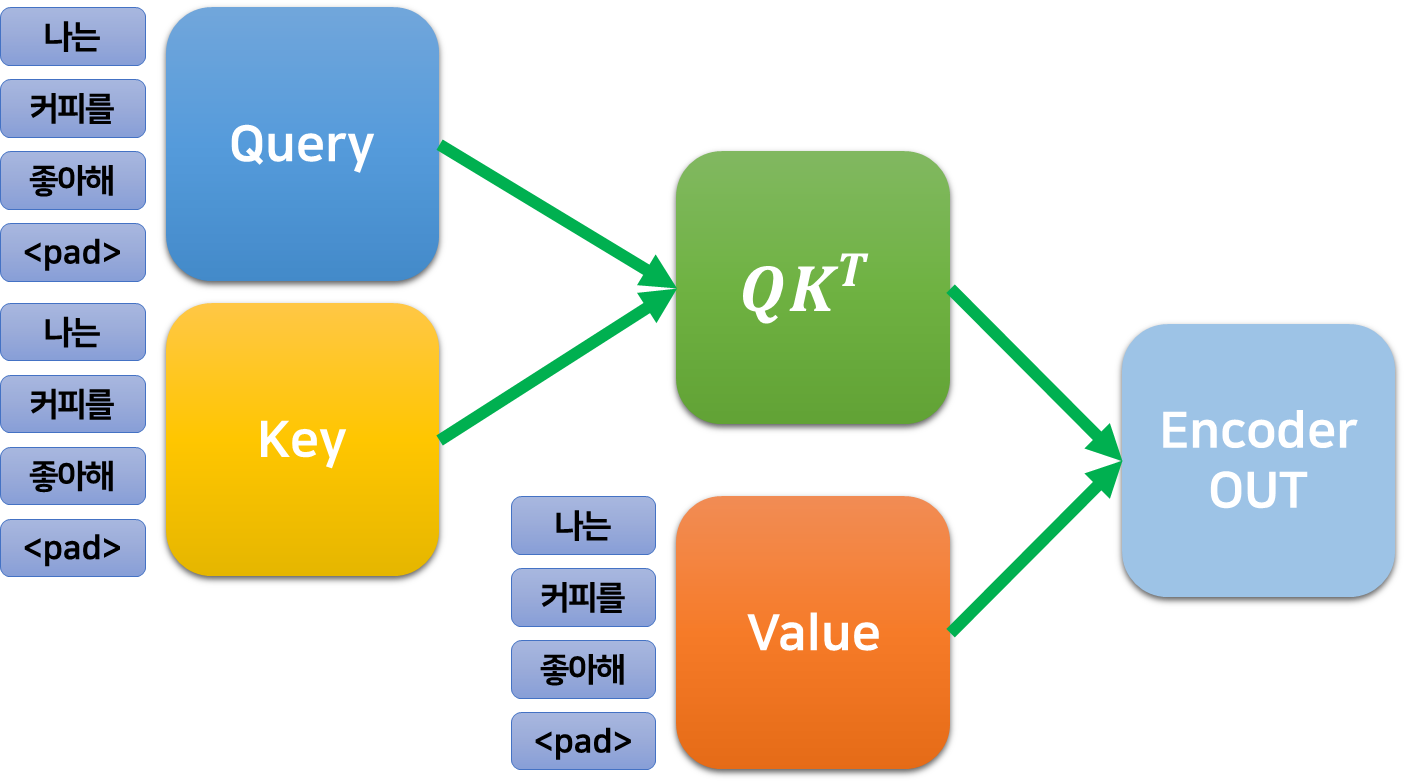
이제 앞서 얻은 행렬 $QK^T$를 벨류 행렬 $V$에 곱한다. $V$ 역시 입력 데이터에서 계산된 행렬이기 때문에, 이를 입력 데이터에 각 단어 간의 관계에 대한 주목도를 주입하여 주는 것으로 이해할 수 있다.

멀티 헤드 어텐션

멀티 헤드 어텐션은, 쿼리와 키의 내적을 $n_{head}$개로 나누어 수행한다.
앞서 $512\times 512$ 크기의 쿼리와 키를 내적 하여 $512\times 512$의 $QK^T$를 얻었는데, 예를 들어 $n_{head}=2$라면 다음과 같이 수행된다.

1. $Q$와 $K^T$를 $n_{head}=2$로 나누어, $512\times 256$, $256\times 512$ 크기의 행렬로 내적을 수행한다.
2. 그 결과, 2개의 $512\times 512$의 $QK^T$, $QK^T_1, QK^T_2$가 얻어진다.
3. 이에 대하여 $V$도 2개의 $512\times 256$ 행렬로 나누어 각 $QK^T_i$와 연산을 수행하면 $512\times 256$의 결과 행렬이 2개 얻어진다.

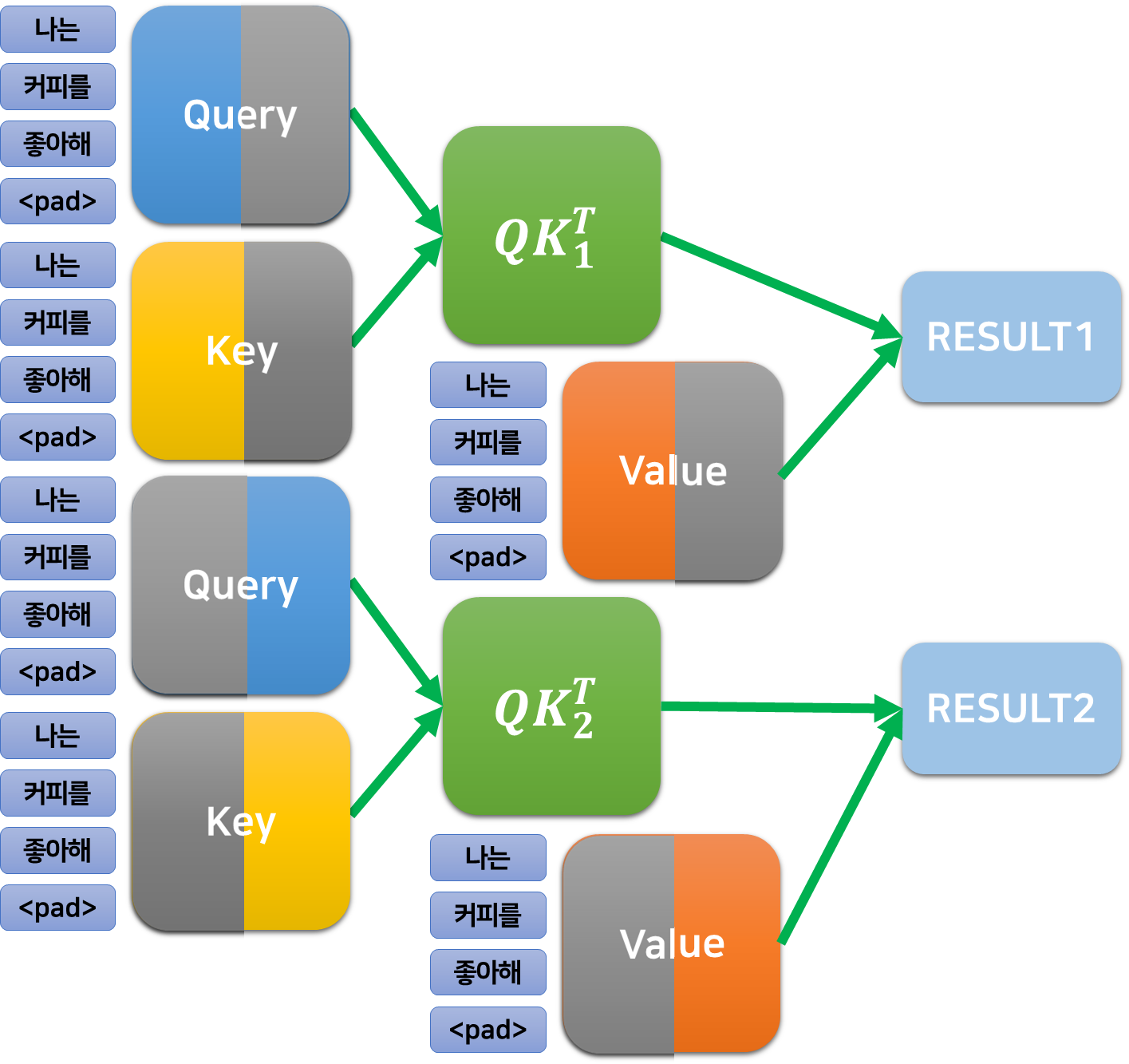
이렇게 어텐션을 나누어 수행하여도 결과적으로는 같은 크기의 출력이 나오는데, 왜 번거롭게 하는가 싶을 수 있다.
저자들은 이러한 trick이 나누어진 Attention Head들이 각각 다른 특성을 학습할 수 있도록 한다고 한다.

어텐션은 Softmax를 통해 후처리 되는데, 이는 큰 값을 갖는 한 두 개의 관계들만이 강조되도록 한다. 이로 인하여 한 Attention Head가 주목하도록 만들 수 있는 관계의 수에는 제약이 생기게 되는데, Multi-Head를 통해 이 수를 늘리는 것이다.

Encoder (Cont.)

앞서 Multi-Head Attention의 결과로 여러 개의 Attention 결과 행렬을 얻었다. 이를 concatenate 하기에 앞서, Residual Connection과 Layer Normalization을 적용해 준다.

Residual Connection은 학습이 안정적이고 빠르게 수렴하게 한다. (자세한 내용은 ResNet 리뷰를 참고하기 바란다.)
Layer Normalization은 각 데이터의 열에 대하여 Normalization을 적용한다.

마지막으로 FC layer 2개와 Layer Normalization, Dropout으로 구성된 Feed Forward Network를 통과한 후, 다시 한번 residual connection과 layer normalization을 적용하면 마침내 하나의 Encoder를 통과했다!

앞서 얘기한 것처럼 인코더의 출력은 인코더의 입력과 같은 크기를 가지기 때문에, 인코더를 통과한 결과를 바로 다시 인코더에 넣을 수 있다. 이렇게 6개의 인코더를 통과하면 마침내 트랜스포머 구조의 반을 지나왔다.

Decoder: Inference

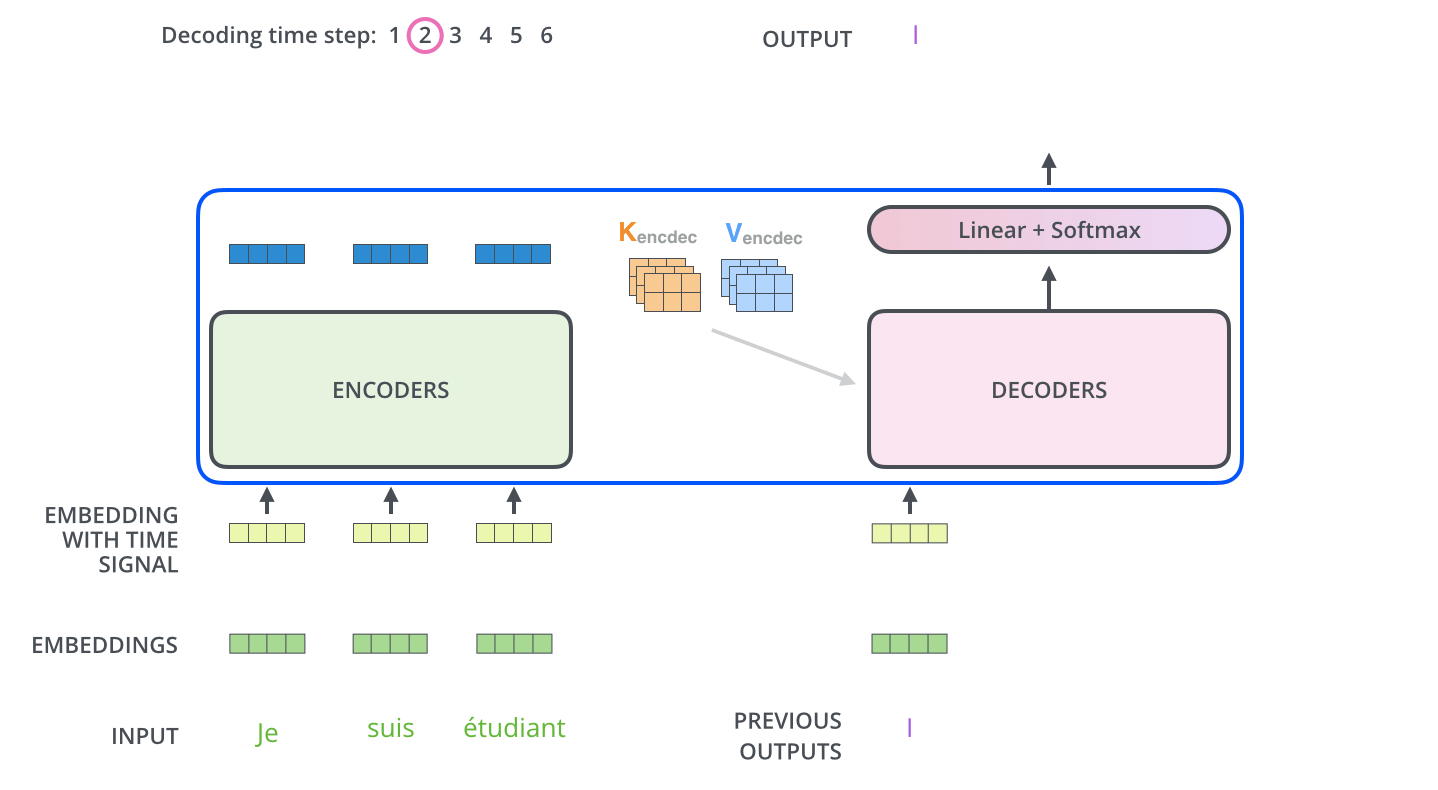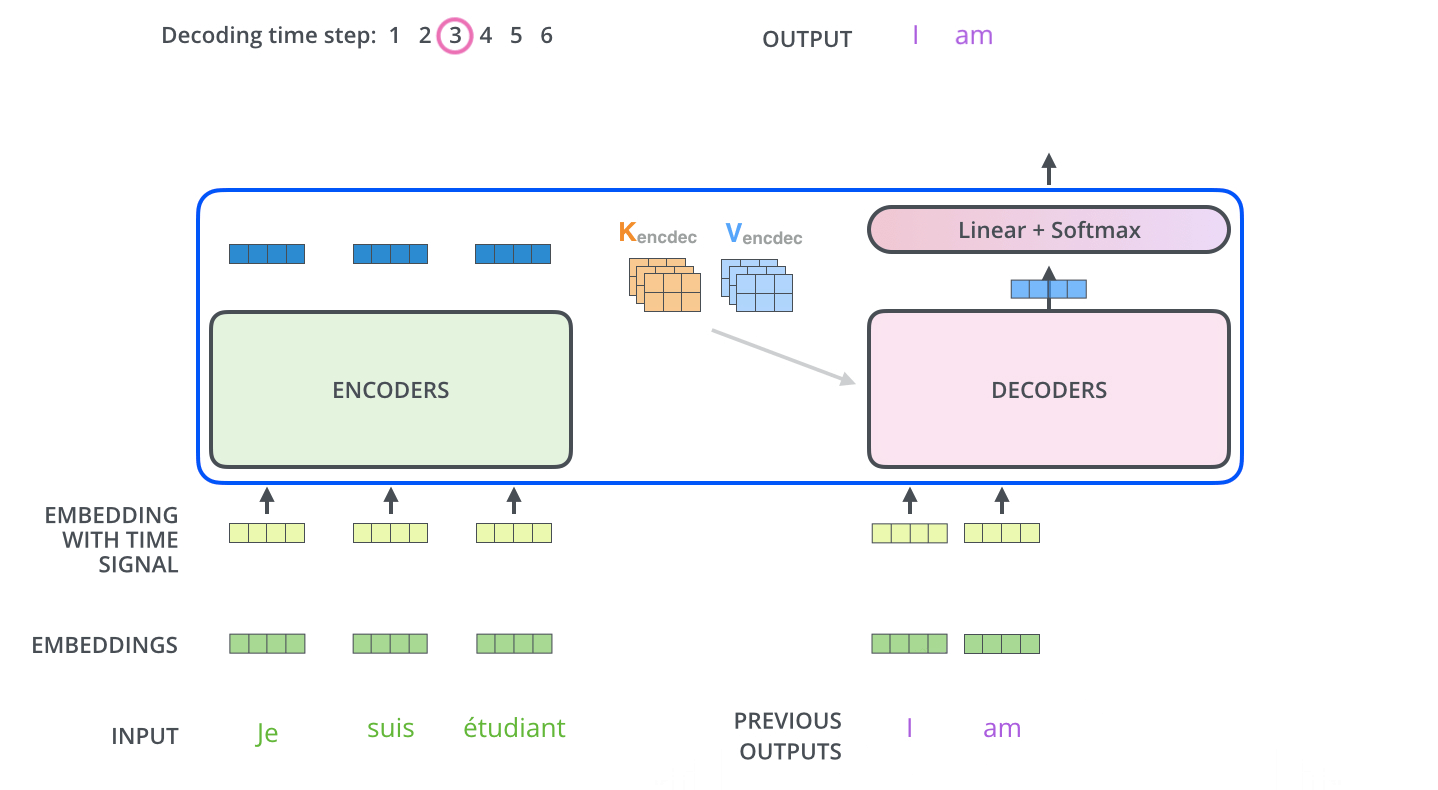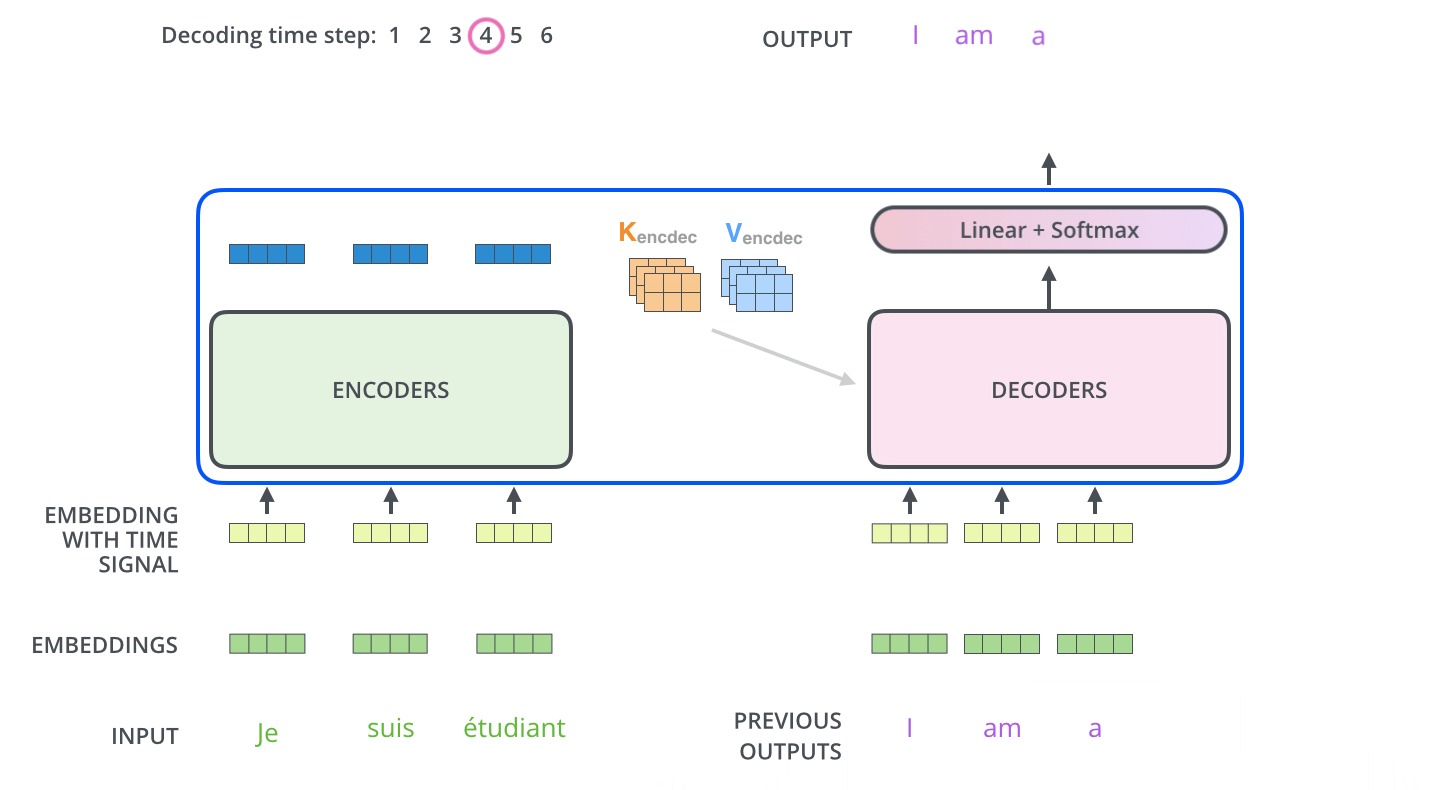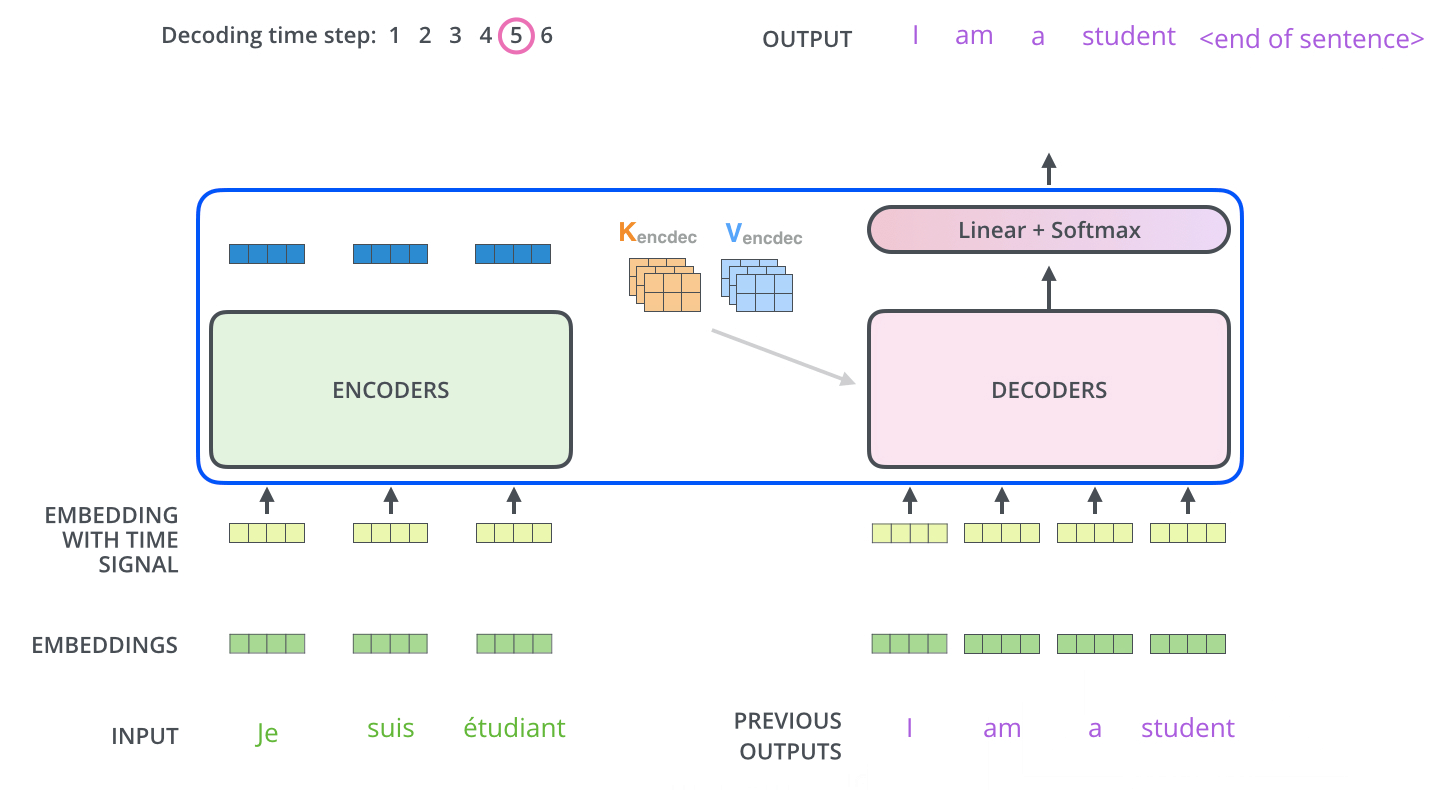
디코더의 이해를 위해선 먼저 추론 시의 동작 원리를 이해하는 것이 좋다. 트랜스포머의 디코더는 입력 데이터에 이어질 토큰을 인코더의 출력을 기반으로 예측한다.

예를 들어, “나는 커피를 좋아해”를 번역하는 트랜스포머 모델의 디코더는 “<sos>”라고 하는 문장의 시작을 의미하는 토큰과 “나는 커피를 좋아해” 문장이 인코더를 거쳐 나온 출력을 입력받고 “I”라는 단어를 출력한다.

그다음, 앞서 출력한 “<sos>I”라는 결과를 다시 입력 삼아 디코더에 입력하여 “love”를 출력으로 얻고, 다시 반복하여 “coffee”를 얻는다. 마지막으로 “<sos>I love coffee”를 입력하면 번역이 완료되었으므로 “<eos>”라고 하는 문장의 끝을 의미하는 토큰을 출력한다.

Decoder: Training

앞서 살펴본 것처럼, 디코더는 출력을 한 토큰 단위로 진행하며, 입력으로 이전에 출력한 내용들을 사용한다.
학습 단계에서는 이를 한 번에 진행하기 위해 정답에 해당하는 데이터(앞선 예시에서 “I love coffee”)를 입력해 주되 masking을 적용한다.

Masked Multi-Head Self Attention

먼저 디코더에 입력된 데이터에 대하여 셀프 어텐션을 수행한다. 만약 입력된 데이터가 “<sos>I love”라면, [“<sos>, “I”, “love”] 세 가지 토큰에 대한 셀프 어텐션이 수행될 것이다.

그런데 학습 단계에서는 번역이 진행 중인 데이터가 입력되는 것이 아닌, 정답 데이터 “<sos>I love coffee<eos>”가 한 번에 입력된다. 그 결과, “love”를 예측할 때는 오로지 이미 출력된 “<sos>”와 “I”의 정보만 알아야 하는데, 아직 출력되지도 않은 “love”와 “coffee”의 어텐션 정보까지 사용할 수 있게 된다. 이를 방지하기 위해, 셀프 어텐션으로 얻은 $QK^T$를 $V$에 곱하기에 앞서 Masking을 진행한다.

위 그림과 같이, $QK^T$ 행렬의 대각 요소의 상단을 매우 작은 값(-1e9)로 masking 함으로써, 미래의 토큰에 대해서는 attention을 할 수 없도록 제한할 수 있다.

이렇게 masking 된 $QK^T$와 $V$를 곱하여 디코더의 입력에 대한 셀프 어텐션을 수행한다. 이때, 디코더에서의 셀프 어텐션 역시 앞서 설명한 멀티 헤드 구조를 갖는다.

Multi-Head Cross-Attention

디코더의 입력에 Self Attention을 적용한 후 인코더와 유사하게 Residual Connection과 Layer Normalization을 수행한다. 이렇게 디코더의 입력으로 얻은 행렬과 인코더의 출력 사이의 크로스 어텐션을 수행한다.

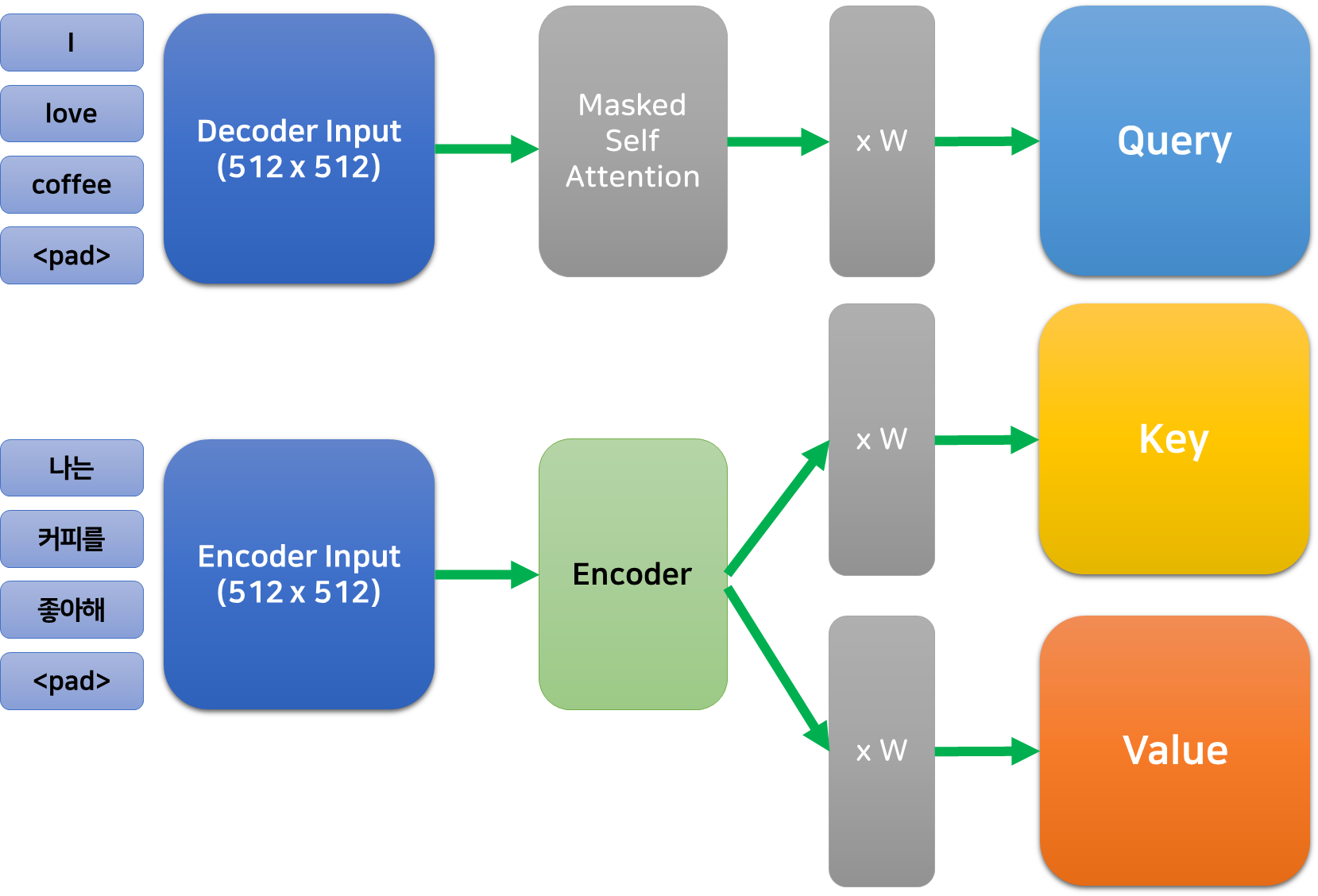
크로스 어텐션은 디코더의 입력으로 얻은 행렬에 가중치를 곱하여 쿼리로 사용하고, 인코더의 출력에 각각의 가중치를 곱해 키와 벨류로 사용한다.

어텐션을 거치고 역시 Residual Connection과 Layer Normalization을 거친 출력은 Feed Forward 신경망을 거쳐 다시 한번 Residual Connection과 Layer Normalization을 거치고, 마침내 Decoder의 출력이 된다. 디코더의 전체적인 구조는 아래 그림과 같다.

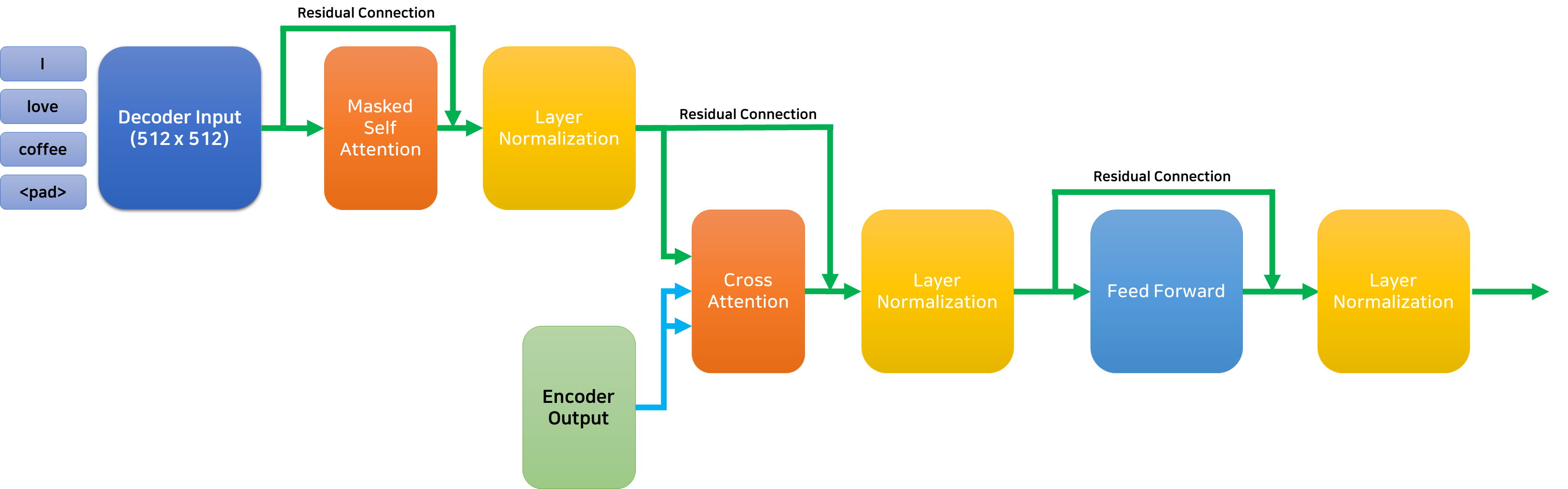
Transformer Architecture

마침내 트랜스포머를 구성하는 모든 요소들을 살펴보았다. 이제 Attention Is All You Need 논문의 Figure 1을 통해 전체적인 구조를 이해해 보자!

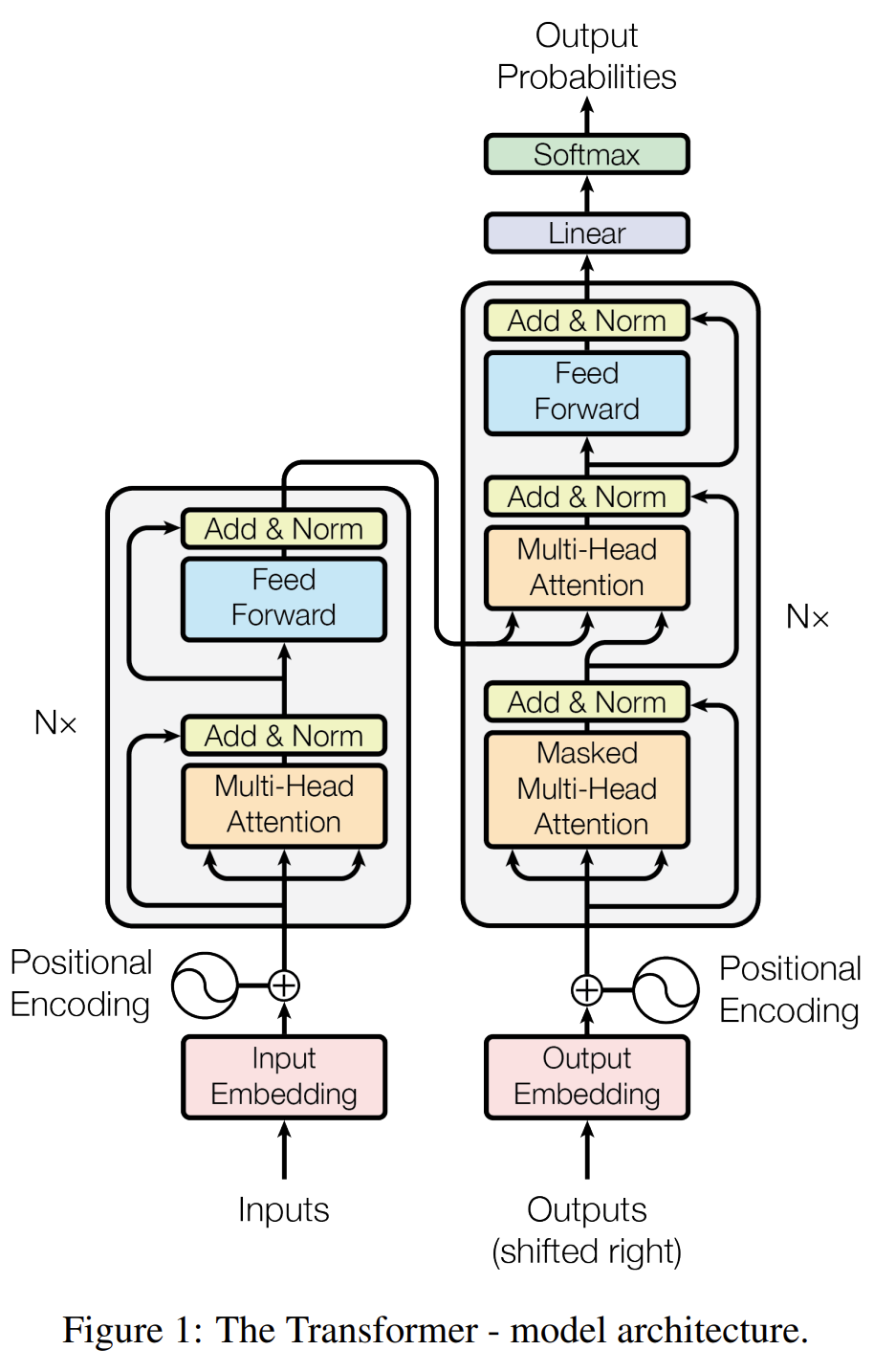
1. 입력 데이터를 임베딩하고, Positional Encoding 정보를 더해준다.
2. 데이터를 인코더에 입력한다.
   1. Multi-Head Self Attention을 수행한다.
   2. Residual Connection & Layer Normalization을 수행한다.
   3. Feed Forward Network를 통과한다.
   4. Residual Connection & Layer Normalization을 수행한다.
3. 인코더의 출력을 입력 삼아, 인코더 N개를 모두 통과한다.
4. 디코더의 입력을 임베딩하고, Positional Encoding 정보를 더해준다.
5. 데이터를 디코더에 입력한다.
   1. Masked Multi-Head Self Attention을 수행한다.
   2. Residual Connection & Layer Normalization을 수행한다.
   3. 인코더의 출력과 Multi-Head Cross Attention을 수행한다.
   4. Residual Connection & Layer Normalization을 수행한다.
   5. Feed Forward Network를 통과한다.
   6. Residual Connection & Layer Normalization을 수행한다.
6. 디코더도 N개를 모두 통과한다.
7.  Linear 계층과 Softmax를 통과하여, 디코더 입력에 이어질 단어를 출력한다.

Ablation Studies

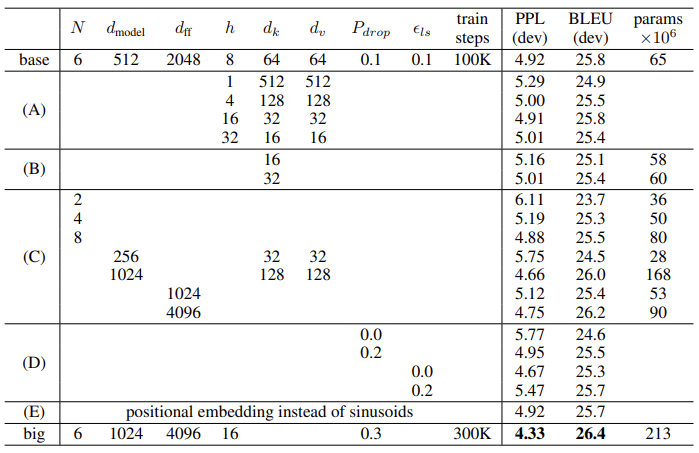
저자들은 트랜스포머의 각 요소들에 대한 비교 실험을 진행하였다.
성능 지표인 PPL은 낮을수록, BLEU는 높을수록 좋다.

• (a)에서, head의 개수 $h$가 증가함에 따라 성능이 증가하지만, 32로 너무 많이 두면 오히려 감소함을 알 수 있다.
• (b)에서, 어텐션 시 key의 크기를 크게 하는 것이 성능에 좋음을 알 수 있다.
• (c)에서, 모델의 성능이 크기와 비례함을 확인할 수 있다.
• (d)에서는 dropout과 label smoothing이 성능을 향상함을 알 수 있다.
• (e)는 positional encoding에 앞서 설명한 삼각함수 방법 대신 학습 가능한 파라미터를 적용한 결과이다.

결론

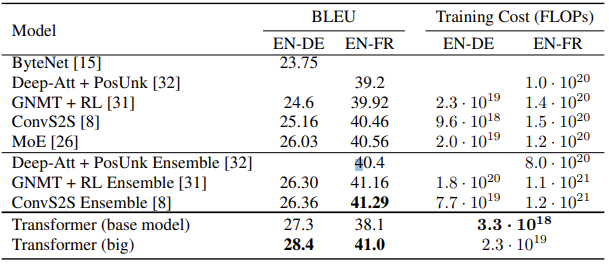
트랜스포머는 (어찌보면 당연히) 당시 존재하던 번역 모델들을 앞서는 SOTA 성능을 보였습니다.
트랜스포머의 등장은 자연어 처리 분야에 충격을 주었고, 이어서 ViT 등이 등장하며 다양한 분야로 충격이 퍼져나갔습니다. 데이터나 task의 형태에 따라 CNN, LSTM 등의 구조를 사용하거나 혼합하는 대신 신경망 전체를 어텐션으로 구성하는 단순한 방법이, 생각보다 너무 강력했습니다.

최근 읽은 제프리 힌튼 교수님의 인터뷰에서, 딥러닝이 인간의 학습 방식과 지능보다 효율적이고 강력하다는 이야기를 읽었습니다. 트랜스포머를 공부하니 비로소 이 말이 이해가 되는 것 같습니다.

다음에는 시간을 들여 트랜스포머의 분석 논문들을 정리하고 ViT를 리뷰해 보겠습니다.

읽어주셔서 감사합니다!