[NeurIPS2021]Batch Active Learning at Scale

Intro

본 논문은 이전 연구에서 고려하지 않았던 large batch size(기존의 약 2배, 100K~1M)를 갖는 active learning 알고리즘을 위한 Cluster-Margin Algorithm이라는 방법론을 제안하는 논문이다. 매우 큰 배치 사이즈는 두가지 도전적 문제를 갖는데 하나는 학습의 각각의 데이터 셋에 대한 민감도 감소, 두 번째는 연산 시 발생하는 병목현상이다. 이러한 문제를 해결하는 해당 논문의 메인 아이디어는 Hierarchical Agglomerative Clustering(HAC)라고 한다. HAC는 배치 내의 모델이 확신도가 낮은 데이터 예제들의 분포를 다양하게 하기 위한 것으로 모든 샘플링 단계의 전처리로 unlabeled data에 한번만 적용하면 된다는 장점을 갖는다. 즉, 데이터셋의 다양성을 강화하여 large batch 학습으로 인한 데이터 중복 등으로 발생하는 학습의 민감도 하락을 막으면서 연산량을 줄일 수 있는 방법론이다. 본 실험은 Resnet-101을 이용한 large scale 실험 뿐 만 아니라, 기존 연구와 비교를 위한 VGG16(CIFAR10, CIFAR100, SVHN) 실험도 같이 리포팅하여 효율성을 보였다.

Method

제안하는 프레임워크인 Cluster-Margin은 3단계로 구성된다: Initialization Step, Clustering Step, Sampling Step. 이때 Clustering Step이 논문의 핵심인 HAC를 포함하는 단계이며 각 단계에 대한 자세한 설명을 이어가겠다.

Step1: Initialization Step

Cluster-Margin은 여느 Active Learning 방법론과 유사하게 Seed set이라고 표현하는 랜덤으로 선정되었다고 가정하는 labeled set(기호: P)으로 학습하여 모델을 초기화 한다.

Step2: Clustering Step

Cluster Step에서는 논문의 핵심인 Hierarchical Agglomerative Clustering(HAC)를 진행하며 위가 그의 작동 알고리즘이다. 이는 전체 데이터 풀(X)에 대해 한번 작동하며 HAC를 통해 cluster set(기호:C)를 생성한다. HAC는 반복적으로 클러스터 중 가장 가까운 두 쌍인 A, B가 threshold인 ϵ(하이퍼파라미터, 엡실론)보다 가까운 경우 병합하는 방식으로 이루어진다.

Step3: Sampling Step

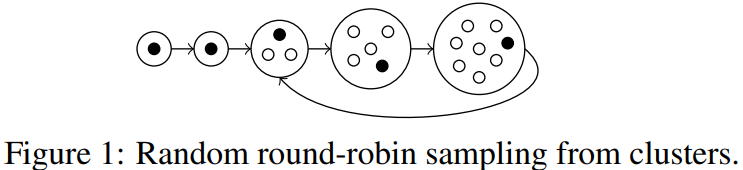
Sampling Step에서는 모델의 확신도가 낮은 데이터셋에서 분포가 다양하도록 선별한다. 즉 uncertainty와 diversity를 모두 고려하기 위한 전략을 설계하였다. 먼저 *margin score(하단 설명)가 낮은 순으로 M개만큼 초기 선별을 한 후, diversity 를 고려하여 목표한 예산만큼 선별하도록 필터링을 한다. 해당 필터링을 위해 Cluster-Margin이 선정한 Round-robin sampling이란, 각 클러스터들을 크기로 정렬한 후 작은 클러스터에서 부터 하나씩 랜덤으로 샘플을 선정한다. 가장 큰 클러스터에서 랜덤으로 데이터 선별을 마친 후에, 다시 뽑을 데이터가 남아있는 가장 작은 클러스터로 돌아가 데이터를 랜덤으로 선정하는 샘플링 방식이다. 가장 작은 클러스터일수록 희박한 분포를 갖는 데이터일 확률이 높다는 가정하에 선정한 선별법이라고 한다. 여기서 클러스터를 구성하는 방식은 margins score로 선정된 인스턴스 M개를 HAC로 선정된 클러스터에 맵핑하여 클러스터 집합을 구성한다. 이때 클러스터 집합에 포함된 인스턴스 갯수가 클러스터의 사이즈이며 구성된 클러스터 집합을 클러스터라고 칭했다.

*margin score: 데이터에 대한 모델의 class 예측값 중 가장 높은 확률로 예측한 클래스의 스코어와 그 다음 높은 확률로 예측한 클래스의 스코어의 차이. 예를 들어 고양이, 개, 토끼를 분류하는 모델이 있을 때 입력 데이터 A에 대해 고양이일 확률 0.6, 개일 확률 0.3, 토끼일 확률 0.1로 예측했다면 A의 margin score는 0.3(0.6-0.3)임.

Experiment

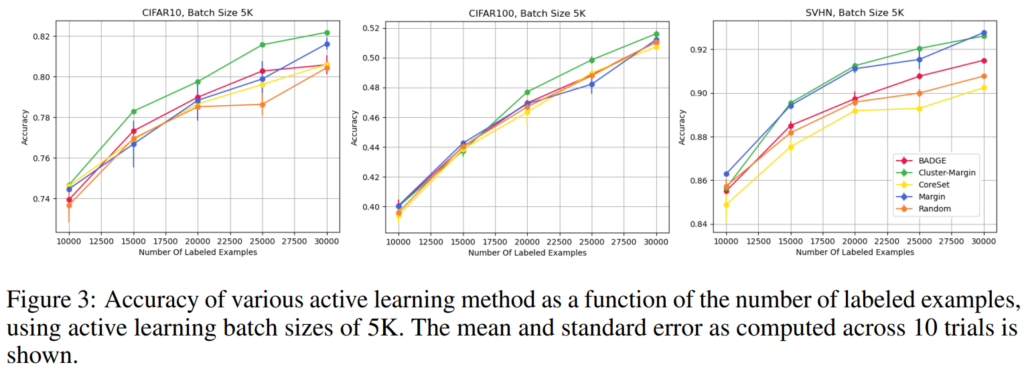
비교실험은 large batch가 가능하도록 설계된 기존 논문중 우수한 성능을 보이는 CoreSet과 BADGE, 그리고 margin sampling 방식으로 uncertainty sampling을 진행한 Uncertainty Sampling, Random sampling 방식을 비교군으로하여 진행되었다. 우선 Active Learning 분야에서 성능 비교에 주로 사용되는 데이터셋인 CIFAR10, CIFAR100, SVHN에 대해서 비교실험은 아래와 같이 진행되었으며 제안하는 방법론이 기존 방법론 대비 우수함을 보였다. LLOSS등 small batch를 타겟으로 설계된 방법론 대비 한 사이클에서 데이터셋이 더해지는 장 수가 큼을 확인할 수 있다. (CIFAR10 데이터셋에서 LLOSS가 cycle 당 1,000장 선별된다면, 아래는 5,000장 선별, LLOSS는 Learning Loss for Active Learning로 small batch active learning 실험을 포함한 우수 논문임)

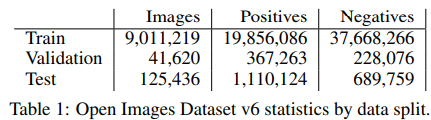
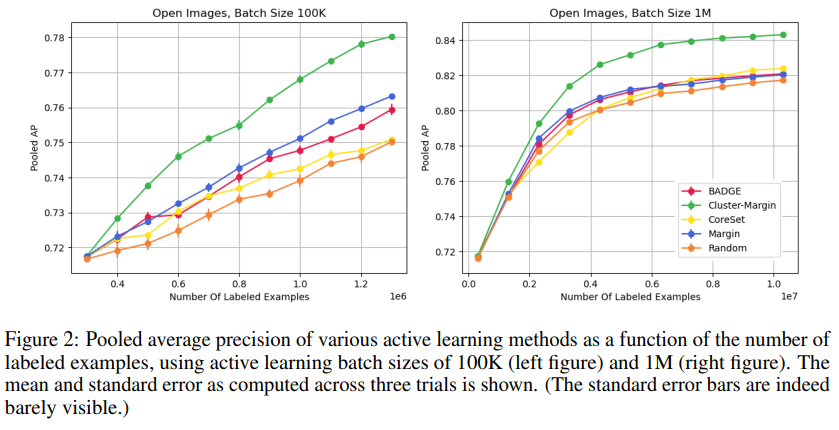
다음으로 실질적으로 논문의 퍼포먼스를 보일 수 있는 배치 사이즈가 매우 큰 상황에 대한 실험에 대한 결과이다. 실험은 Open Images v6에 대해 진행되었으며, 데이터셋에 대한 정보는 위(Table1)과 같다. 좌측이 한 사이클마다 100K(100,000)개, 우측이 한 사이클마다 1M(=1,000,000)개의 데이터를 선별해 labeled pool에 추가한 것이며, 제안하는 방법론이 이러한 large batch setting 실험에서 우수한 성능을 보임을 실험을 통해 보였다.

Related Work

인공지능 모델은 많은 양의 데이터를 경험으로 학습하여 입력데이터에 대해 학습 데이터에 기반한 예측을 생성한다. 따라서 모델은 데이터에 대한 의존도가 높다. 그러나 모델을 학습하기 위한 데이터를 생성하는 일은 (1)모델에게 부족한 데이터(x)가 무엇인지 알아야 하며 해당 데이터에 대해 예측하길 바라는, 즉 데이터에 상응하는 라벨(y)을 함께 제공해야 하기에 (2)어노테이션 작업을 필요로해 그 생성 비용이 높다. 이에 대한 다양한 해결책이 있으며 Active Learning 역시 그 중 하나이다. Active Learing이란 가공되지 않고 단순 수집된 Unlabeled Pool에서 모델이 학습해야 할 데이터 x를 직접 선별하여 라벨링을 요청하는 방법론으로 (1)에 해당하는 데이터 선별 작업의 비용을 없애고, 어노테이션 할 데이터를 효율적으로 선정할 수 있다는 장점을 갖는다. Active Learning 연구는 다양하게 세분화되곤 하는데 특히 해당 논문에서는 Batch Size를 기준으로 나눌 수 있다. Active Learning의 프로세스는 1. 모델 초기화/2. 고가치 데이터의 선정/3. 고가치 데이터의 라벨링/4. 모델 재학습으로 구성되며 해당 프로세스를 하나의 주기(Cycle)로 하여 N번 반복한다. (그동한 리뷰했던 많은 논문에서는 CIFAR10 데이터에 대해 10번 반복실험을 리포팅 한다.) 이때 선정되는 고가치 데이터의 크기가 큰 경우와 작은 경우로 분류할 수 있는데, 해당 논문은 특히 큰 경우에 이점이 있도록 설계되었다. 해당 논문의 결과와 비교된 CoreSet, BADGE 는 모두 Diversity 까지 고려한 논문이며, 제안 논문도 Diversity 고려를 위해 round robin sampling 기법을 도입한 것으로 보아 large batch를 위해서는 diversity를 고려하는 것이 일반적이라는 인사이트를 얻을 수 있다. 다만 의야한 점은 Figure2에서 Margin based 방법론도 성능이 상당이 높은데 이는 uncertainty based 방법론이라는 점이다. Cluster-Margin 방법론 역시 margin score를 통해 우선 high uncertainty instance를 선별하고 선별된 데이터셋 중 다양성을 고려하였다. 즉, 단순 diversity 보다는 uncertainty를 고려하는것이 large batch setting에서 좋다고 해석된다. 정리하자면 어노테이션 예산이 충분하여 데이터를 선별할 때는 uncertainty 를 기반으로 우선 선별하되, 선별 된 데이터 중 diversity를 최대로 선정해아한다는 것이다. 이를 위해 사용된 기법인 round robin sampling이 흥미로웠고 다만 uncertainty의 중요도를 판별하는 M에 대한 hyperparameter가 꽤 중요한 변수였을 것 같다. Figure3의 실험에서는 M=1.25t, Figure 2 실험에서는 M=10t (t는 라벨링 예산)으로 세팅되는데, 이에 대한 다양한 실험이 같이 있었다면 더 좋았을 듯 하다.