[AAAI 2022] UFPMP-Det: Toward Accurate and Efficient Object Detection on Drone Imagery (Part. 2) (See also, [ICCV 2019] SoftTriple Loss: Deep Metric Learning Without Triplet Sampling)

안녕하세요. 열 세번째 X-Review입니다. 이전 주차 Part. 1 리뷰에 이어 UFPMP-Det의 MP-Det Method 파트를 작성하겠습니다. MP-Det의 Contribution은 명확하지만, 수학적인 고찰을 포함해야하므로 쉽지 않을 것으로 예상됩니다. 이 때 MP-Det (Multi-Proxy Detection Network)을 이해하고자 2019년, ICCV의 SoftTripple Loss에 대한 이해가 선제되어야할 것 같아 해당 논문을 간략히 소개하고자 합니다. SoftTripple Loss 논문에 대해 기존의 HardTripple Loss에 대한 문제 제기, 본 논문의 Contribution 및 방법론을 소개하겠습니다.

Multi-Proxy Detection Network

MP-Det의 메인 아이디어는 “intra-class variance를 극복하고자 SoftTripple Loss에서 영감을 받은 Multi-proxy classification head를 도입한다”입니다. 해당 메인 아이디어를 이해하려면 SoftTripple Loss와 Multi-proxy의 의미를 알아야합니다. SoftTripple Loss를 이해하지 않고선 아래의 수식에 대한 이해가 불충분하기 때문이죠. 문득 보면 Softmax에 s_i^k 를 곱한 후 Sigmoid 연산을 해주는 것으로 보이는데… 해당 수식이 가지는 의의에 대해서는 의문점이 듭니다. 그러므로 우선, SoftTripple Loss 논문을 살펴보겠습니다.

P_r(Y = y_i | x) = \sigma(\gamma \sum_k{\mathrm{exp}(s_i^k) \cdot s_i^k \over \sum_{k=1}^K \mathrm{exp}(s_i^l)}) \quad \cdots \quad(1)

[ICCV 2019] SoftTripple Loss

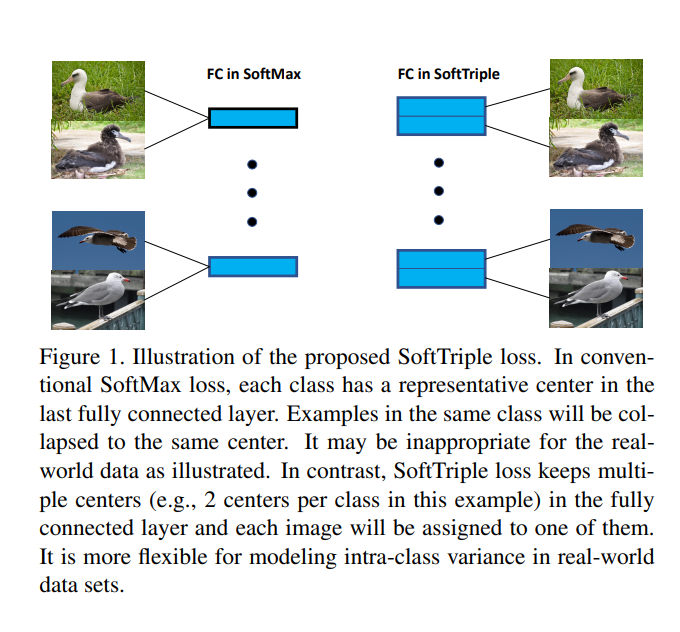
해당 논문의 주된 Contribution은 본 논문의 Multi-Proxy Classification Head를 이해하는데에 도움이 됩니다. Multi-Proxy Classification Head는 전통적인 Detection Network의 Classification Head는 i번째 카테고리에 Single weitght vector인 w_i 를 할당합니다. 이는 다시 말해 Backbone에서 나온 Feature x 가 있을 때, 해당 ㅌ x 가 i번째 카테고리와 일치할 조건부 확률을 의미합니다. 이는 아래 수식 (2)로 표현할 수 있습니다.

P_r(Y = y_i | x) = \mathrm{Sigmoid}(w_i^Tx) \quad \cdots \quad (1)

사실, Fully-Connected Layer를 통과하고 Sigmoid를 통해 Classification을 진행하는 당연한 이야기입니다. 논문에서는 기존 방식을 single proxy classifier라고 합니다. 암묵적으로는 각 카테고리는 오직 하나의 클래스 센터인 w_i / ||w_i|| 에 할당되도록 추정됩니다.

하지만 드론 이미지에서는, 동일 클래스에서도 다양성이 존재합니다. 이를 Part 1에서 Intra-class Variance라는 용어로 소개했었는데, 그 이유는 드론의 비행 고도, 운용 중 다양한 요인 등으로 인해 View point와 View change, 그리고 Instance의 사이즈가 다양해지기 때문입니다. 이러한 경우, 한 Instance는 하나의 클래스 센터가 아닌 몇몇 클래스 센터에 걸쳐져있는 것 처럼 보여 분류 시 혼동을 줄 수 있습니다. 그러므로, 본 논문의 저자는 SoftTriple Loss 논문에서 아이디어를 차용해와 i번째 카테고리가 K개의 [w_i^1, w_i^2, \dots, w_i^K] Proxy (Center)를 가지고 있다고 가정합니다.

이제 다시, Triple Loss 논문으로 돌아옵니다. Triple Loss에서는 Softmax와 Triplet Loss의 유사성을 입증하며 Triple Loss를 제안합니다. 해당 과정이 굉장히 복잡한데, 이번 리뷰의 처음이자 끝으로 보입니다. 사실 본 논문의 핵심 Contribution 중 하나지만, Triple Loss, Transportation plan (최적 운송 이론)등을 통해 MP-Det을 끌고 오지만 해당 내용이 굉장히 어려워, 실험 파트를 위주로 설명하도록 하겠습니다.

먼저 Softmax입니다. 수식은 너무나도 잘 알고 있겠지만, 굳이 한번 써 보겠습니다. 입력 벡터 x_i 가 y_i 클래스에 속할 조건부 확률을 다음과 같이 나타낼 수 있습니다. 아래 수식 (3)의 [w_1, w_2, \dots, w_K] 는 마지막 Fully-Connect Layer를 통과한 Weith을 의미합니다. Softmax에서는 해당 확률을 통해 하나의 클래스로 명합니다.

P_r(Y = y_i | x) = \sum_k{\mathrm{exp}(w_{y_i}^Tx_i) \over \sum_i^j \mathrm{exp}(w_j^Tx_i)}) \quad \cdots \quad(3)

Softmax Loss는 아래 수식 (4)로 표현할 수 있습니다. 또한, Sotmax를 Normalization한 Loss는 수식 (5)로 표현됩니다. 수식 (5)는 Normalization을 계산한 \lambda 를 통해 Softmax를 Normalization 합니다.

\mathcal{L}_{softmax}(x_i) = -\mathrm{log} \sum_k{\mathrm{exp}(w_{y_i}^Tx_i) \over \sum_j \mathrm{exp}(w_j^Tx_i)}) \quad \cdots \quad(4)

\mathcal{L}_{softmax_{norm}}(x_i) = -\mathrm{log} \sum_k{\mathrm{exp}(\lambda w_{y_i}^Tx_i) \over \sum_j \mathrm{exp}(\lambda w_j^Tx_i)}) \quad \cdots \quad(5)

이제 Triplet Loss입니다. Triple Loss 또한 다들 알고 계시듯 기준 샘플 Anchor와, Anchor와 동일한 클래스인 Positive, Anchor와 다른 클래스인 Negative를 샘플링하여 정한 다음, Anchor와 Positive는 가까워지는 방향으로, Anchor와 Negative는 멀리 떨어지도록 하는 방향으로 학습하도록하는 Loss를 의미합니다. 이 때 거리는 주로 Cosine Similarity 기반 Euclidean Distance가 사용됩니다.

이를 쉽게는 L = max(d(a,p) - d(a,n) + margin, 0) 으로 나타냅니다. 수식으로는 아래 (6)으로 나타낼 수 있습니다. 이 때 margin은 Positive와 Negative 사이의 여백을 나타냅니다.

\forall_{i,j,k}, ||x_i - x_k||_2^2 - ||x_i - x_j||_2^2 \ge \delta \quad \cdots \quad(6)

위 수식 (6)에서 \delta 는 margin을, x_i, x_j, x_k 는 차례로 Anchor, Negative, Positive를 의미합니다. 이 때, 각각의 x가 모두 Unit Vector일 때, 즉 ||x|| 가 1일 때는, 위 수식을 (7)로 단순화하여 표현할 수 있습니다.

\forall_{i,j,k},  x_i^Tx_k - x_i^Tx_j \ge \delta  \quad \cdots \quad(7)

위 수식 (7)은 코사인 유사도에서 x_i , x_j , x_k 의 거리가 1이며 벡터 연산 식으로 표현한 결과입니다. 코사인 유사도 수식을 써보면 바로 도출될 수 있습니다. 이제, Triplet Loss는 다시 다음 수식 (8)과 같이 표현할 수 있습니다.

\mathcal{L}_{triplet}(x_i, x_j, x_k) = [\delta +  x_i^Tx_j - x_i^Tx_k]_{+} \quad \cdots \quad(8)

위 수식 (8)의 목적은 x_i^Tx_j 는 감소하는 방향으로, x_i^Tx_k 는 증가하는 방향으로 학습하도록 유도됩니다. Triple Loss의 저자는 두 Softmax, Triple Loss 사이의 연관성을 입증하며 다음과 같이 말합니다. “Minimizing the normalized softmax loss with smooth term delta is equivalent to optimizing a smoothed trple loss.” 즉, Normalized Softmax와 Triplet Loss를 줄이는 것과 같다고 언급합니다. 이를 이해하는 것이 곧 SoftTiple Loss를 사용한 본 논문의 MP-Det을 이해하는 것의 최종입니다.

저자는 이를 증명하고자 Normalized Softmax를 표현하는 수식 (9)를 언급합니다. 수식 (9)의 p는 Distribution Over Class로 해당되는 클래스의 확률을 1, 해당하지 않으면 0으로 만드는 Term이며 H(p)라는 Entropy Regularization을 더합니다. 수식 (9)는 Triple form을 포함하면서 Normalized Softmax로 귀결됨을 증명하기 위한 수식입니다. 물론, SoftTriple Loss를 위한 단계이기도 합니다.

\mathcal{L}_{softmax_{norm}}(x_i) = \mathrm{max}_{p \in \vartriangle} \lambda \sum_j p_jx_i^T(w_j - w_{y_i}) + H(p) \quad \cdots \quad(9)
\\
\vartriangle = \left \{P | \sum_j p_j = 1, \forall_j p_j \ge 0 \right\} \quad \cdots \quad(9-1)

위 식의 x_i^T(w_j - w_{y_i}) 는 Triplet form입니다. 핵심은 Triple form을 포함하는 식이 Normalized Softmax와 동일함을 보여주어 두 Loss를 줄이는 방향이 같다는 것을 보여주는 것입니다. 이를 증명하기 위해서는 K.K.T Condition에 따라 P가 closed-from solution을 가진다는 것을 통해 증명할 수 있습니다. K.K.T Condition에 따라 수식 (9)가 Normalized Softmax Loss와 같음을 보이는 방식입니다. 사실 이를 이해하긴 하였으나, K.K.T Condition에 대한 선제적인 이해가 부족하여 완전한 이해에 도움을 드리지 못해 죄송할 따름입니다ㅎㅎ

최종적으로 저자는 하나의 클래스가 K개의 Center를 가지고 있을 때, 입력 벡터와 클래스 C간의 유사도 (S)를 Triplet Form과 Softmax For을 이용하여 다음 수식 (10)의 SoftTriple Loss를 제안합니다.

\mathcal{L}_{softTriple}(x_i) = -\mathrm{log} {\frac{\mathrm{exp} (\lambda (S^{'}_i, y_{i} ) - \delta) } {\mathrm{exp} (\lambda(S^{'}_{i, y_i} - \delta) + \sum_{j \ne y_i}\mathrm{exp}(\lambda S^{'}_{i, j}))} }  \quad \cdots \quad(10)

수식 (10)은 본 논문의 Multi-prixy conditional 수식 form인 (1)과 동일합니다. 이제, i번째 클래스에 대한 Decision-boundary는 단일 Center가 아닌 Multiple Center, 즉 Multiple-proxy로 표현됩니다. 이를 통해 Intra-class variance로 인한 Classfication 성능의 저하를 방지하고, 성능을 높이고 있습니다.

본 논문의 MP-Det은 이외에도 Multiple Proxy가 학습 중 결국 Unit한 Proxy로 붕괴되는 것을 방지하고자 최적 운송 계획 이론을 도입합니다. 최적 운송 계획 이론 (Optimal Transportation Plan)을 통해 \mathcal{L}_{ot} 를 다음 수식 (11)과 같이 정의합니다. 수식 (11)은 최적 운송 계획을 그대로 표현한 수식으로, 최적 운송 계획을 이해한다면 쉬울 수 있겠지만, 해당 이론 자체가 워낙 수학적인 고찰이 담긴 문제임에.. 개인적으로는 이해가 되지는 않았습니다. 따라서 현재는 수식만 작성 후, 추후 보충설명 하겠습니다.

\mathcal{L}_{ot} = \frac{1}{N_c} \sum_{i=1}^{N_c} tr (C_i^TP_i^*) \quad \cdots \quad(11)

Loss는 최종적으로 전통적인 Detection Loss와, Optimal Transport Loss, 그리고 Contrastive learning을 Classification에 포함한 세 Loss의 합으로 표현됩니다. \mathcal{L} = \mathcal{L}_{det} + \mathcal{L}_{ot} + \mathcal{L}_{cl} .

다음은, 실험으로 넘어가겠습니다. 실험에서는 앞서 언급드린 VisDrone과 UAVDT 데이터 셋을 사용했으며, 실험은 MMDetection 프레임워크에서 행했습니다. 최근 MMDetection 프레임워크를 통해 다른 모델을 원복 중, 해당 논문의 모델 또한 원복 중에 있는데, 원복이 완료된다면 코드 분석을 통해 이전에 이해하지 못한 부분을 코드를 통해 살펴보도록 하겠습니다.

Experiments

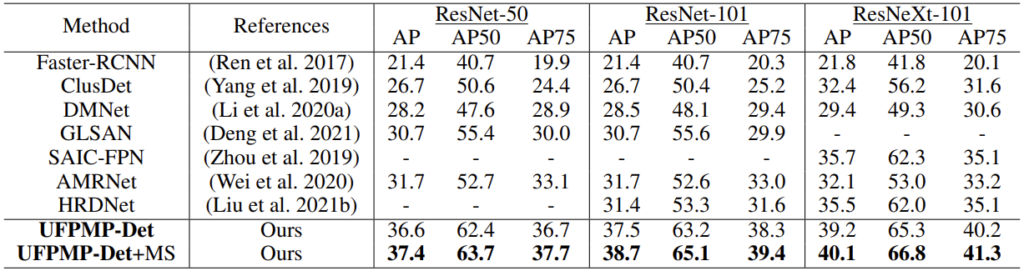
우선, SoTA 논문과의 비교입니다. SoTA에 비해 성능이 높아졌다는 것을 언급하고 있습니다. MS는 Multi-scale Trick으로, 하나의 이미지에 대해 최적의 Scale을 통해 Inference하는 방식을 의미합니다. 사실 UFPMP-Det+MS는 유의미하다고 보이지는 않습니다.

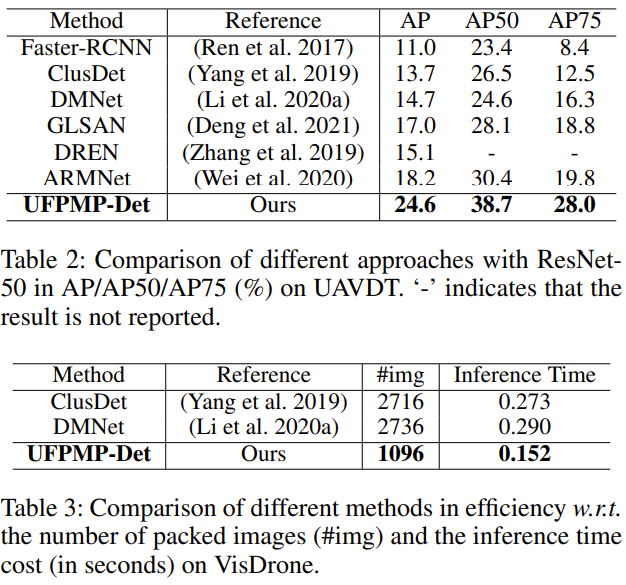
다음은 ResNet 50을 백본으로 사용하는 방법론들과의 비교입니다. AP가 전체적으로 상승했으며 특히 평균 AP가 가장 높아졌는지에 대해, Small Object에 대한 성능이 높아졌음을 의도하고자 한 것으로 보입니다. 저자의 Clustering은 최초의 방식이 아닌, 이전의 ClusDet 등에서 사용된 방식인데, #img라는 측정 치로, 패킹한 이미지의 수를 통해 Part 1에서 언급한 모자이크 시 최적의 방법을 통해 Packed image의 수를 높이는 것에 유의미한 결과를 얻을 수 있다는 것을 의미합니다.

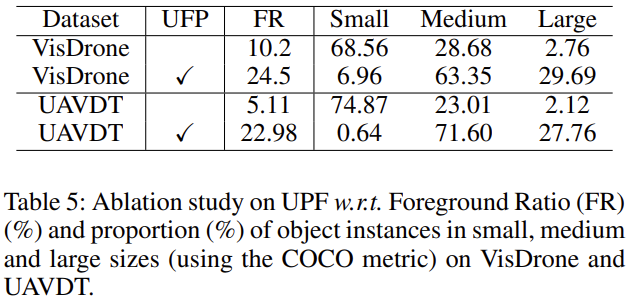
개인적으로는 위의 실험 테이블이 가장 인상 깊었습니다. UAVDT에서 UFP 모듈을 적용했을 때의 Foreground Ratio 및 Small, Medium, Large 사이즈의 비율을 말하는데, Enlarged Packing 방식을 통해 Inference 시 Small object로 판단되는 비율이 급격히 줄어듦을 알 수 있습니다. 이로 인해 Foreground Ratio가 높아짐을 알 수 있습니다. UAV 아이디어를 적용하고 싶은 제게는, 가장 좋은 실험 테이블인 것 같습니다.

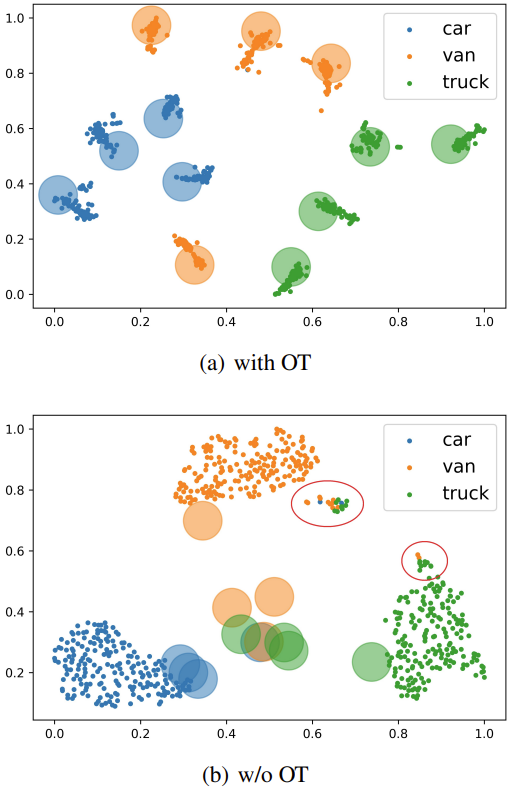
마지막으로 정성적 자료입니다. 클러스터링 및, Small object에 대해 Enlarge한 모습을 통해 UAV 모듈의 효과를 알 수 있습니다. 아래는 Optimal Transportation을 통한 t-SNE 자료입니다. Optimal Trasportation을 통해 Class간 Clsutering을 효과적으로 수행했다고 하는데, 해당 지식이 불충분하여 아직 아쉽습니다.

요즘 Detection 논문을 읽다보면, 예전의 혹은 수학적인 지식을 고도로 필요하는 듯한 느낌이 듭니다. 그만큼 새로운 Contribution 등을 위함이라 생각이 드나, 현 수준에서 최신 SoTA의 수학적 고찰을 이해하긴 아직 쉽지 않은 것 같습니다. 하지만 해당 논문에 굉장히 관심이 깊기 때문에 주기적으로 글을 업데이트할 예정입니다. 부족하지만 읽어주셔서 감사합니다.