[NeurIPS2022]LADA: Look-Ahead Data Acquisition via Augmentation for Deep Active Learning

Intro

해당 논문은 data augmenation과 active learning을 결합한 논문입니다. 두 방법론은 모두 딥러닝 모델의 학습 데이터가 부족한 상황에서 이를 효과적으로 해결하기 위한 대책입니다. 두 접근법이 어떻게, 얼마나 모델에 효과가 있을지 비교할 생각을 못해보았던것 같은데요. 해당 논문은 두 방법론을 효과적으로 결합하기 위한 프레임워크를 제안합니다. 조금 더 자세하게 들어가 보겠습니다.

Related work

Data augmentation(데이터 증강)

데이터에 flipping, rotation과 같은 변환을 주어 분포를 일부 변화시킴으로써 labeled data의 수를 증가시키는 방법론인 데이터 증강은 가장 일반적으로 학습 데이터 부족을 해결하기 위한 해결책입니다. 최근에는 생성모델을 통한 데이터 증강 연구로도 확장되었습니다. 또한 deep learning model을 통한 데이터 증강이 가지고 있는 한계인 제한된 다양성 문제를 돌파하는 Mixup과 같은 방법론도 제안되었습니다. 제한된 다양성 문제란, deep learning model이 특정 labeled data를 변환시키고, 해당 라벨에 해당하는 데이터의 분포, 패턴을 보존한 채로 변환을 진행한다는 의미인데요, 예를 들어 mixup 방법론은 강아지로 라벨링된 이미지 A와 고양이 이미지라고 라벨링 된 B를 통해 새로운 분포의 데이터 C 를 만들때 새로운 라벨 “고양이x0.5 + 강아지x0.5″을 부여합니다. 이처럼 mixup은 데이터 증강기법이 특정 라벨의 데이터를 생성한다는 다양성의 한계의 지평을 넓힙니다.

Active Learning(능동학습)

active learning은 많은 학습 데이터 후보 중에서 가장 정보량이 많은 데이터를 선택하여 효율적으로 딥러닝 모델을 학습시키기 위한 방법론으로 데이터의 정보량을 측정하기 위한 습득함수에 대한 연구가 다양하게 진행되고 있습니다. 정보량 측면에서 기존 학습 데이터의 분포적 다양성을 넓히기 위한 diversity based 방법론과 학습 경계면의 불확실성이 높은 데이터를 찾기 위한 uncertatinty based 방법론이 있습니다.

Pipelined approach

본 논문에서 언급하길, 데이터 부족 현상을 해결하기 위한 두 가지 접근법인 data augmentation과 active learning 방법론을 결합하는 것은 너무 당연한 것이라고 합니다. [11]이 대표적인 pipelined approach 중 하나인데요, active learning으로 선별된 데이터에 augmentation을 적용하여 효과적으로 모델을 학습시키는 방법론 입니다. 본 논문은 해당 방법론을 더 발전시켰는데, 기존 방법론은 selected data(active learning을 통해 선별한 데이터)를 증강하여 얻는 데이터의 정보량을 고려하지 않았습니다. 본 논문은 Look-Ahead Data Acquisition via augmentation(LADA)를 제안하여 선별함수가 데이터 증강된 이후의 데이터가 모델 학습에 미칠 효과를 미리 고려하여 데이터를 선별합니다.

Method

Problem formulation
본 논문에서는 classifier network parameter인 θ를 학습합니다. 따라서 classifier인 f_θ를 생성합니다.
습득함수인 f_aug(x,f_θ)는 데이터 x에 대한 score를 출력으로 합니다.

Detail

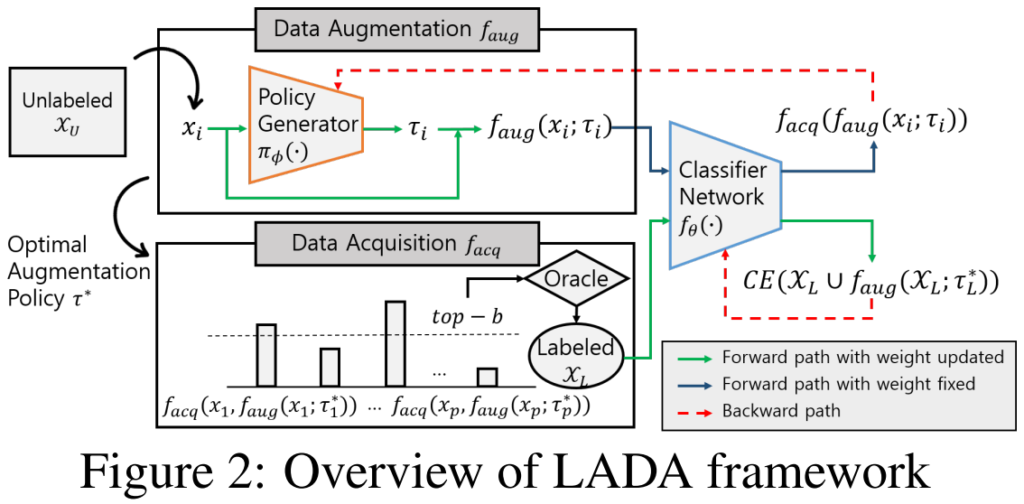
제안하는 프레임워크, LADA는 위와같이 두 갈래로 구성됩니다. data augmentation에 관여하는 f_aug와 active learning에 관여하는 습득함수 f_acq입니다. f_aug는 f_acq의 점수가 높게 되는 augmentation 방법론인 최적 τ(최적τ=τ*)를 찾게 되는데, 그 수식은 아래와 같습니다.

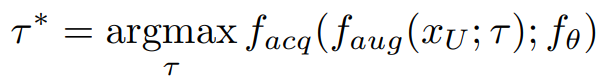
위 방식으로 최적의 증강방식 τ*를 찾은 후, 이를 적용한 unlabeled data의 f_acq 점수를 활용해 데이터를 선별하며 그 수식은 아래와 같습니다.

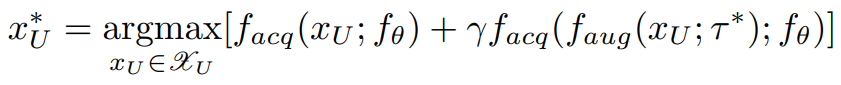
전체 unlabeled data의 집합인 X_u에서 real-world data인 x_u와 이로부터 유래한 가상 데이터, f_aug(x_u, τ*) 각각의 f_acq로 측정한 점수를 통해, 점수가 높은 데이터를 학습할 데이터로 선택합니다. 표기의 단순화를 위해 f_aug와 f_acq 함수를 통합해서 f_integ라고 칭하겠습니다. 이는 augmentation을 고려한 unlabeled data의 acquisitions score(f_acq의 점수)함수로 augmentation을 고려한 선별함수를 도입한 LADA에서 제안한 함수를 간단화한 것입니다.

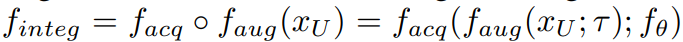
τ*를 찾기위한 τ 풀은 다양하게 구성될 수 있습니다. 그 중 본 논문에서는 새로운 변환 기법인 InfoSTN와 InfoMixup를 제안합니다. 각 기법에 대한 소개는 아래와 같습니다.

InfoSTN

STN(Spatial Transformer Networks)은 classifier network에 도입되어 사용되는 학습가능한 neural network 구조입니다. 즉 데이터 x를 augmntation 하기 위해 네트워크 파라미터 θ를 구성하는 함수 f_θ라고 볼 수 있습니다. 자세한 STN 연구의 디테일은 후에 해당논문[8]을 읽어보아야 겠지만 간단히 소개하자면 STN은 미분 가능한 변환방법으로 데이터의 변환 방식을 학습가능하도록 합니다. STN은 3가지 프로세스로 진행됩니다(아래 그림 참조).
1) localization network를 통한 변환
2) grid 생성(출력이미지로부터 입력이미지 내 좌표 그리드를 생성)
3) sampler(공간 변환 파라미터를 입력 이미지에 적용)

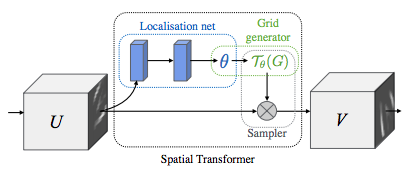
위의 프로세스를 수식화하여 한번 더 설명하자면 아래와 같습니다.

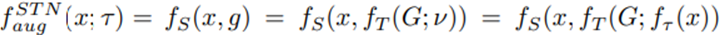
즉 STN은 sampling 된 grid인데 이 grid는 localization network에서 생성된 네트워크 f입니다. (자세한 샘플링 기법 등은 원 논문[8]을 참고해주세요)

LADA는 STN을 active learning에 접목하여 acquisition function의 feedback으로 학습하는 InfoSTN을 제안합니다. InfoSTN은 파라미터인 정책τ를 학습하는데, 목적함수는 아래와 같습니다.

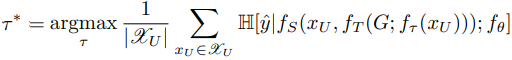
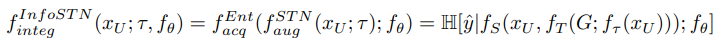
unlabeled data들의 f_integ 점수가 높아지는 최적 정책인 τ를 찾도록 구성되는 것이지요. STN에서 τ는 원래 labeled data에 대해 cross-entopy loss를 최소화하는 방식으로 학습했었는데, 이는 classifier를 최대로 활용하는 방식입니다. 그러나 제안하는 방법은 최적의 augmentation space를 탐색하는것을 목적으로 하며 active learning의 주기마다 classifier가 변화합니다. 따라서 본 논문에서는 acquisition iteration 초반에 변환 파라미터 τ를 저장해놓고 classifier 학습시에 이를 도입한다고 합니다.

이 함수를 적용한 습득함수(acquistion function, max entropy)는 아래와 같이 구성됩니다.

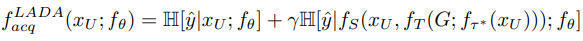
좌측 항이 real-world data에 대한 점수, 우측 항은 변환된 데이터에 대한 점수를 의미합니다. 위 방식으로 측정된 score에 대해 점수가 높은 데이터 부터 허용 가능한 라벨링 예산만큼 데이터를 선별합니다. 이후 선별된 데이터에 대해 저장한 변환 함수 τ로 data augmentation을 적용하여 효과적으로 모델을 학습하게 됩니다. 논문에서 H는 entorpy를 통해 계산된 점수입니다. 전통적인 습득함수인 entropy는 아래와 같이 정의됩니다.

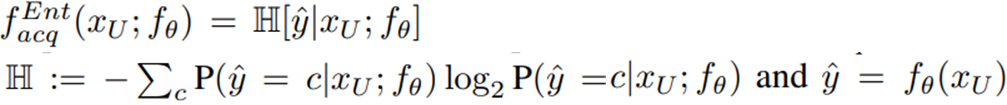
그러나 본 논문은 기존의 여러 연구에 대해 습득함수를 확장하 수 있으며 기존의 유명한 연구인 Variational Adversarial Active Learning (VAAL, ICCV2019), Learning Loss for Active Learning (LL4AL, CVPR2019) 등에서 제안한 습득 함수를 실험에 이용합니다. 여러 방법론에 적용할 수 있는 확장성이 제안 연구의 장점 중 하나입니다.

InfoMixup

Mixup은 label에 대한 augmentation을 허용하여 가상 데이터셋이 가질 수 있는 데이터 다양성의 분포를 획기적으로 넓힌 data augmentation 연구입니다. 본 논문에서는 두번째 augmentation 방법론으로 mixup을 활용한 InfoMixup을 설계하였는데, active learning이 가상 데이터에 대해 어느정도의 다양성까지 허용할 수 있는지 비교하기 위한 설계인 것 같습니다. InfoMixup 역시 augmentation을 위해 mixing policy, τi를 학습합니다. InfoSTN과 다르게 해당 방법론은 데이터 mixing을 위해 두 데이터가 필요합니다.

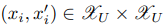
최적의 변환 전략인 τ_i*를 찾는 목적함수는 아래와 같습니다.

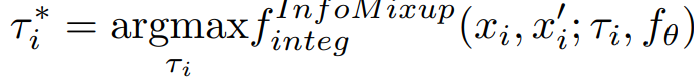
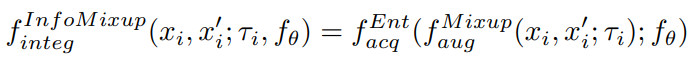
i번째 페어인 x_i와 x_i’을 통해 생성된 데이터 f^mixup_aug(x_i, x_i’;f_θ) 중 f_acq(=mix entropy)가 가장 높은 데이터를 선별하게 됩니다.

이 함수를 적용한 습득함수(acquistion function, max entropy)는 아래와 같이 구성됩니다.

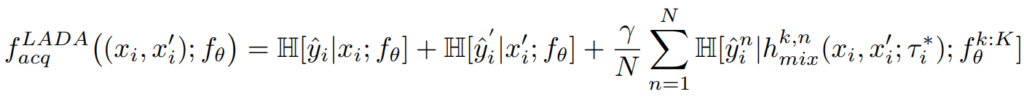
i번째 pair를 구성하는 각 인스턴스의 정보량(1항, 2항)과 pair를 통해 생성된 가상 데이터의 정보량(3항)의 가중치 합으로 구성되며 이때 가중치γ는 데이터셋 마다 다른 하이퍼 파라미터입니다.

Experiment

실험은 Fashion MNIST, SVHN, CIFAR-10, CIFAR-100에 대해서 classification task로 수행되었으며 모든 데이터셋에 대해 γ=1으로 설정했습니다. 단 CIFAR-10의 EntSTN 세팅에서는 예외적으로 γ=0.3로 설정했다고 합니다. 비교 실험을 위한 방법론으로는 1) Random, 2) BALD [18], 3) Coreset [26], 4) BADGE [27], 5) Max Entropy [16], 6) Variation Ratio [17], 7) VAAL [19] and 8) LL4AL [20]를 사용하였으며 CAL[21], BGADL[11], Manifold Mixup[14], AdaMixup[15]은 기 제안된 piplined approach 입니다. 논문에서는 LADA의 프레임워크에서 augmentation network의 학습 여부에 따른 효과를 분석하기 위해 τ를 학습한 버전과 학습하지 않는 버전인 fixed를 모두 리포팅하였습니다. 아래 ablation study에서 볼 수 있듯이 InfoSTN의 후기 사이클의 일부를 제외하고는 τ가 학습하였을 때 가장 높은 성능을 보임을 알 수 있습니다.

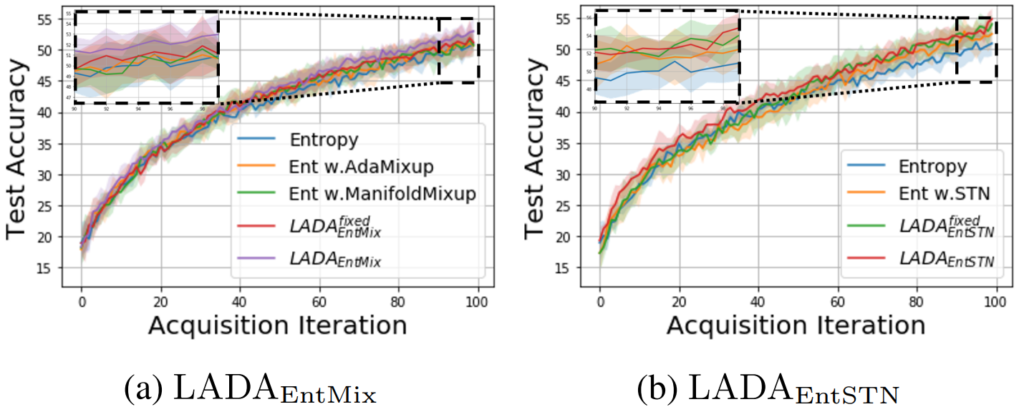
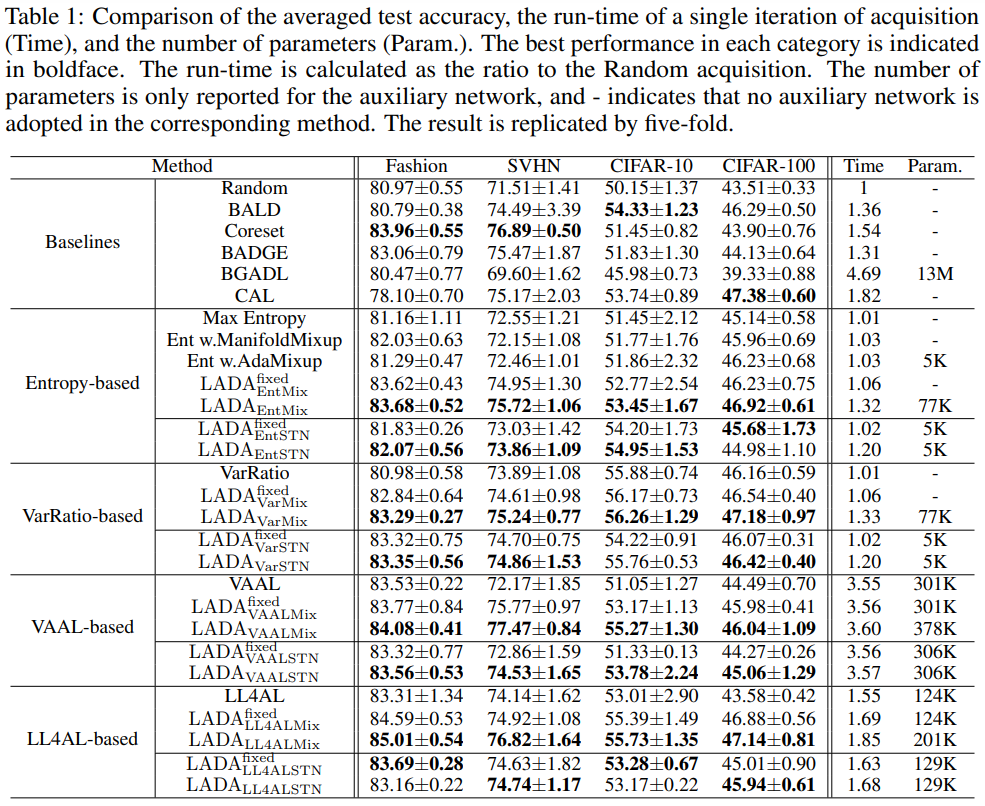
정량적 결과로 Table1에서 확인할 수 있듯이 단순히 기존 active learning 방법론을 적용하는 것 보다 제안하는 LADA를 접목한 습득함수를 이용하였을 때 성능향상이 있는것을 볼 확인할 수 있으며, CIFAR-100을 제외하면 기 제안된 piplined approach 보다 높은 성능을 보임을 확인할 수 있습니다.

앞서 예측햇던 것 처럼 augmenatation의 정도가 active learning 전략에 일관적으로 영향을 미치는 지에 대해서는, 실험 결과에서 알 수 있듯이 InfoMixUp과 InfoSTN중 어느 하나가 일관적으로 성능이 우세하지 않습니다. 따라서 data augmentation 정도에 따른 수용력은 데이터셋이나 active learning 방법론에 의존성이 있음을 알 수 있습니다.

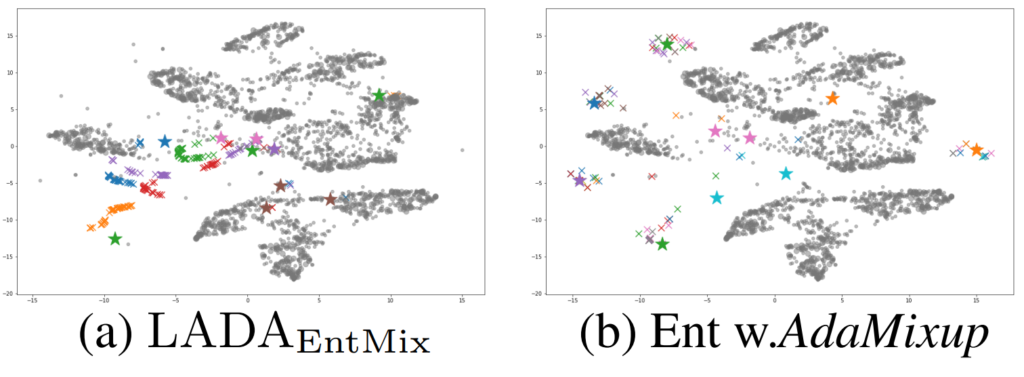
다음으로 논문에서 제안하는 방법론을 이용하였을 때 선택된 데이터의 augmentation 결과가 의미있음을 tSNE를 통해 보였습니다. 가상 데이터의 분포가 클래스에 대한 정보력이 없다고 생각될 정도로 흩뿌려진 (b)와 다르게 (a)는 가상 데이터가 class 단위로 유사한 embedding space에 분포되어있음을 확인할 수 있습니다. 이때 x가 가상데이터이며 별 모양이 real data 이며 색은 class 구분을 의미합니다.

Reference

본 리뷰의 레퍼런스는 원 논문의 레퍼런스 번호를 유지합니다.

[8] Spatial transformer networks.
[11] Bayesian generative active deep learning
[14] Manifold mixup: Better representations by interpolating hidden states
[15] Mixup as locally linear out-of-manifold regularization
[16] A mathematical theory of communication
[17] Elementary applied statistics: for students in behavioral science
[18] Bayesian active learning for classification and preference learning
[19] Variational adversarial active learning
[20] Learning loss for active learning
[21] Consistency-based semi-supervised active learning: Towards minimizing labeling cost
[26] Active learning for convolutional neural networks: A core-set approach
[27] Deep batch active learning by diverse, uncertain gradient lower bounds