[CVPR 2016] NetVLAD: CNN architecture for weakly supervised place recognition

두 번째 x-review입니다. 본 논문은 아마 연구실 내의 모든 사람들이 알고 있을 법한 논문인 .. NetVLAD 논문입니다. 바로 리뷰 시작하도록 하겠습니다. ㅎ ,, ㅎ

Introduction

Visual Place Recognition(VPR)은 영상이나 이미지를 기반으로 장소를 인식하고 식별하는 task이며, 일반적으로 qeury image와 database image를 비교하여 가장 유사한 image의 위치를 이용하여 query image의 location을 추정합니다. ((a)와 유사한 이미지인 (b)를 찾아냄)

기존 Visual place recognition(VPR)에 대해 저자가 언급한 문제점은, 어떻게 하면 도시나 국가 scale의 지역에서 어떻게 같은 street인지 우리가 알아낼 수 있냐는 것과 더불어 시간에 따라 변하는 appearance와 조광에 따라 recognition을 잘 할수 있냐는 것입니다.

이때 CNN이 recognition 분야에서 강력한 image representation으로 등장하게 되었습니다. 그렇기에 저자는 place recognition task에서 CNN을 사용하고자 하였고, 다음의 3가지 Challenge를 소개합니다.

• 장소 인식을 위한 좋은 CNN architecture는 무엇일까 ?
• 학습에 사용되는 많은 양의 data는 어떻게 모을까 ?
• 어떻게 end-to-end 방식으로 학습할 수 있을까 ?

첫 번째 문제를 해결하기 위해서 mid-level(conv5)에서 나온 feature를 하나의 벡터로 표현하는 CNN architecture를 제안했습니다. 이를 위해 VLAD에서 영감을 받아 NetVLAD layer를 설계하게 되었습니다. 이 NetVLAD layer는 모든 CNN architecture에 쉽게 연결할 수 있으며, 기존 VLAD의 미분 불가능한 점을 해결한 것으로 backpropagation을 이용하여 학습할 수 있게됩니다.

다음으로 두 번째 문제인 ‘학습에 사용되는 많은 양의 data는 어떻게 모으는가’에 관한 문제는 Google Street View Time Machine에서 다른 시간 다른 viewpoint로 같은 장소를 찍은 사진을 모아 large dataset으로 만듦으로써 해결하게 되었습니다.

마지막으로 weakly labelled Time Machine imagery에서 end-to-end 방식으로 parameter를 학습해가는 learning procedure를 개발했습니다. 이를 통해 나온 representation은 자동차나 사람같은 여러 이미지에서 자주 등장하는 confusing 요소들을 무시하고, 이미지의 relevant part(skyline, building facades etc..)에 초점을 맞춰 학습하며, 동시에 viewpoint와 조도 변화에 강인하게 됩니다.

Method overview

앞에서 VLAD에서 영감을 받아 netVLAD를 제안한 저자는 place recognition task를 image retrieval로 보게 됩니다. 먼저 “image representation extractor”로 동작하는 function f를 설계하는데 이는 database내 이미지 {I_{i}}에 대해 사이즈가 고정된 벡터인 \mathbb{f}(I_{i})를 추출해내며, 곧 cnn architecture를 의미합니다.

이제 미리 전체 이미지 database {I_{i}}에 대한 representation을 전부 추출해냈으면, 이후 query image representation을 추출해낸 다음 test time에서 query image와 database 내의 벡터화된 이미지를 비교하여 가장 가까운 이미지를 찾아냄으로써 동작하게 됩니다. 이때 거리를 비교할 때는 Euclidean distance를 사용합니다. 즉 이미지 \mathbb{q}와 I_{i}의 거리 d(\mathbb{q}, I_{i})가 작을수록 두 이미지가 비슷한 이미지라고 할 수 있습니다.

이전에 Bag of words vector나 VLAD vector에서 추출되는 hand-engineered image representation(SIFT descriptor)과 달리 저자는 아까 앞에서 언급한 \mathbb{f}({I}) 즉 CNN architecture를 통해 나온 representation으로 end-to-end 학습을 시킴으로써 place recognition 문제를 해결합니다.

Deep architecture for place recognition

대부분의 image retrieval 파이프라인은 (1) local descriptor를 추출하고, (2) 순서에 상관없이 pooling하는 방식(orderless pooling)을 취하는 것입니다. 여기서 orderless pooling이란 추출한 local descriptor들은 일반적으로 이미지에 여러 위치에서 나타날 수 있는데, retrieval에서는 object의 위치 정보보다는 object 자체 특징에 집중해야 하기 때문에 local descriptor들을 위치에 상관없이 합치기 위해 사용되는 것입니다. 결국 orderless pooling 과정을 통해 local descriptor들의 통계 정보를 계산해서 하나의 대표 벡터로 만드는 과정이죠.

이런 방식은 occlusion과 translation에 강인한데, 조도와 viewpoint 변화에 대한 강인함은 descriptor의 특성 때문이며 multiple scale에 대해 descriptor를 추출하기 때문에 scale에도 invariance하게 됩니다.

이렇게 추출한 representation을 end-to-end 방식으로 학습하기 위해서 먼저 저자는 (1) CNN의 마지막 convolution layer 즉, fc layer전 단계까지만 가져가도록 crop한 후 이를 dense descriptor extractor로 봅니다. fc layer를 제와한 convolution layer의 마지막 단의 output은 H x W x D size의 feature map을 가지는데 여기서 D는 H x W 크기의 location에서 추출한 descriptor의 차원입니다. (2) 다음으로 저자는 Vector of Locally Aggregated Descriptor(VLAD)에서 착안된 새로운 pooling layer를 소개합니다. 이 pooling layer는 추출된 descriptor를 고정된 image representation으로 pooling하고 backpropagation 과정을 통해 parameter를 업데이트 해 나가며 학습하는 layer입니다. 이 저자가 고안한 새로운 pooling layer가 ‘NetVLAD’ layer입니다.

NetVLAD: A Generalized VLAD layer (f_{VLAD})

bag-of-visual-words(BoVW)의 aggretation이 visual word를 세는 방식인 반면에 VLAD는 descriptor와 그에 상응하는 cluster center간의 잔차를 합함으로써 vector를 정의하게 됩니다. 일반적으로 D차원을 가지는 N개의 local image descriptor가 input, K개의 cluster center(visual word)가 VLAD parameter일 때 VLAD image representation V은 K * D 차원입니다. 이 행렬 V는 이후 vector로 바뀌게 되고 normalization 과정을 거친 후 image representation으로 사용되게 됩니다. VLAD Vector는 다음과 같은 수식으로 계산됩니다.

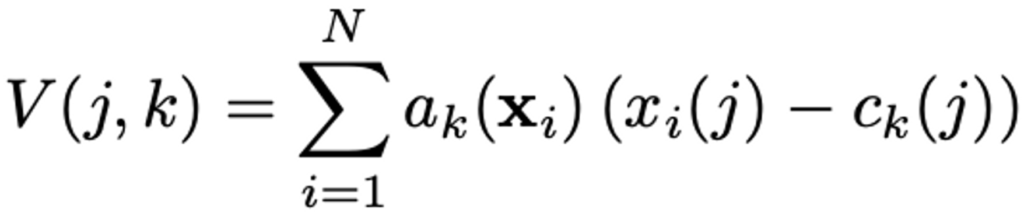
위 수식에서 a_{k}(\mathbf{x}_i)는 descriptor x_{i}와 k번째 visual word간의 관계를 나타내게 되는데, cluster c_{k}가 descriptor x_{i}와 가장 가까운 cluster이면 1의 값을 가지고 나머지는 전부 0의 값을 가지게 됩니다.

하지만 이 a_{k}로 인하여 미분이 불가능하기 때문에 end-to-end로 학습할 수 없게 되며 저자는 이를 해결하기 위해 (미분 가능하게 하기 위해) 다음과 같은 식으로 변경하여 hard assignment에서 soft assignment로 대체하게 됩니다. 여기서 hard-assignment란 입력 데이터를 명확하게 하나의 클러스터에 할당하는 방식이며, soft-assignment는 입력 데이터를 여러 클러스터에 대해 확률적으로 할당하는 방식을 의미합니다.

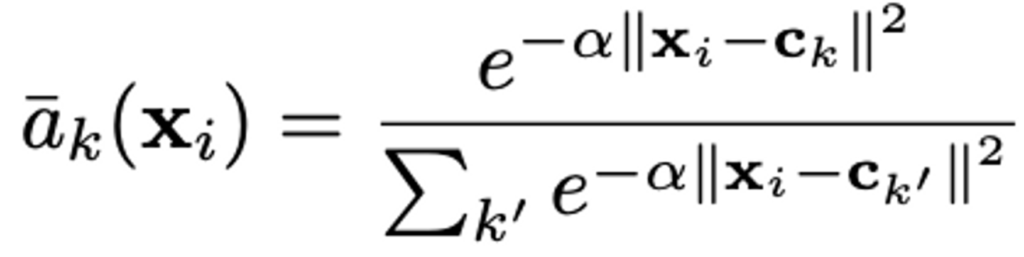
이를 통해 descriptor x_{i}의 weight는 여러 cluster 중심과의 근접성에 비례하게 가져가게 됩니다. a_{k}(\mathbf{x}_i)의 범위는 0에서 1 사이의 범위이며, 가장 가까운 클러스터 중심에 가장 높은 가중치가 할당됩니다.

식에서 α는 거리의 magnitude에 따른 반응의 deacy를 조절하는 파라미터입니다. α가 커질수록 원래 VLAD의 a_{k}처럼 가장 가까운 cluster centre일 때는 1, 그렇지 않을때는 0을 나타내게 됩니다.

이제 위 식에서 분자 분모에 겹치는 부분을 제거하면 최종적으로 아래와 같은 식이 나옵니다.

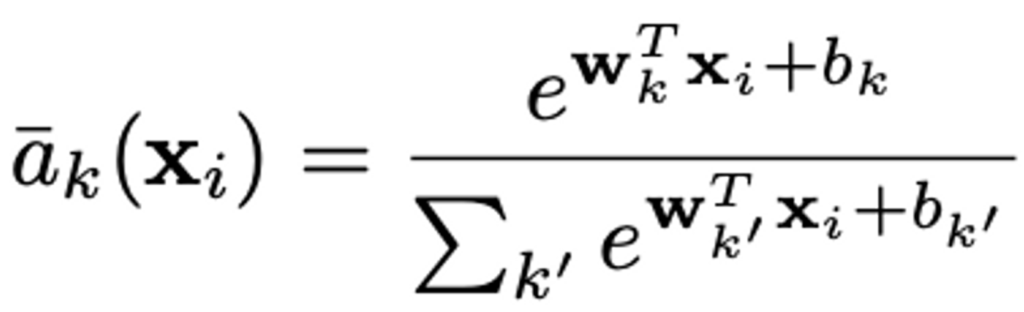
다들 아시다시피 이 수식은 softmax와 같습니다. (아래에 수식 참고)

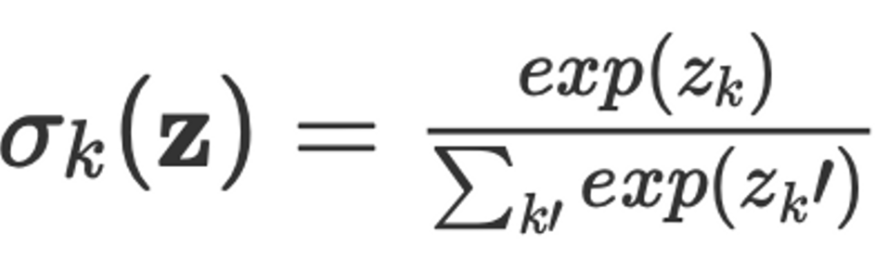
최종적으로 VLAD 식에 새로 정의한 a_{k}를 대입하면 아래와 같은 식이 완성됩니다. 원래 파라미터가 {c_{k}} 1개였지만 이제 {w_{k}}, {b_{k}}, {c_{k}} 3개로 늘어났기에 original VLAD보다 높은 flexibility를 가지게 된다고 하네요.

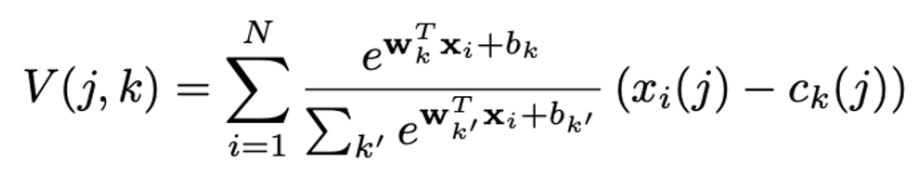
이제 가장 가까운 cluster centre만 보는 것이 아니라 거리에 따른 비율을 고려하여 멀리 떨어져 있는 cluster centre와의 차이도 함께 고려함으로써 hard assignment의 불연속성이 제거되어 미분 가능하게 됨으로써 backpropagation을 통해 학습할 수 있는 것이죠.

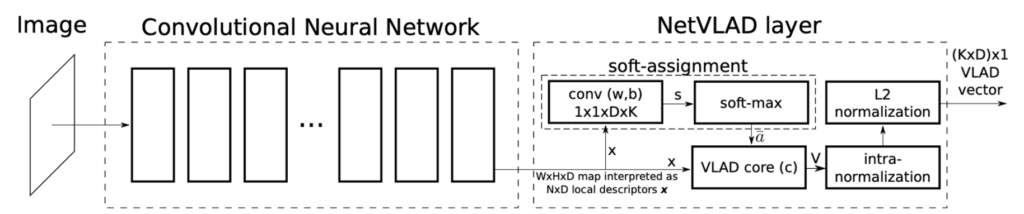
앞에서 계속 설명해온 architecture를 도식화 한 것입니다.

먼저 Image가 들어오면 convolution layer를 통해 N x D 크기의 local descriptor x가 output으로 나오게 되며 convolution operation의 parameter인 weight와 bias를 이용하여 s_{k}(X_i) = w_k^T\mathbf{x}_i + b_k를 계산합니다. (그림에서 conv(w, b) 박스) 이후 softmax함수에 태워 a_{k}를 계산한 후 이를 각각의 (x_{i} – c_{k})와 곱해 V를 구한 후 normalization 과정을 거쳐 최종 (K x D) x 1 크기의 VLAD vector를 산출해내게 됩니다.

Learning from Time Machine data

지금까지는 저자가 제안한 plcae recognition을 위한 image representation 방식을 알아보았습니다. 이제 저자가 제안한 CNN architecture가 어떻게 end-to-end 방식으로 학습하는지 알아봅시다. 여기에는 두가지 challenge가 언급됩니다.

1. 학습에 사용되는 많은 양의 annotation된 data를 어떻게 모을까
2. place recognition task에 사용될 적절한 loss는 무엇일까

첫 번째 문제는 Google Street View Time Machine을 통해 서로 다른 시간에서 촬영된 같은 장소에 대한 데이터를 모아 해결했으며, 두 번째 문제는 새로운 weakly supervised triplet ranking loss를 제안함으로써 해결하였습니다.

Weak supervision from the Time Machine

Google Street View Time Machine은 앞에서 말했듯 지도에서 가까운 위치에서 서로 다른 시간에 촬영한 여러 street-level panoramic image를 제공합니다.

위 사진이 Google Street View Time Machine이 제공하는 image 예시들입니다. 각 열은 서로 다른 시간에 촬영한 인근 위치의 이미지이며, 이 이미지로 학습함에 따라 viewpoint와 lighting 변화에 invariance하고, moderate occlusion을 처리하며, 자동차나 사람같은 혼동되는 시각적 정보를 억제하는 표현 방법을 학습할 수 있습니다.

각 Time Machine panorama 이미지는 GPS 정보도 함께 제공하고 있는데, 저자는 여기서 GPS 정보는 train query q와 지리적으로 가까운 이미지인 potential positive {p_i^q} 그리고 query에서 지리적으로 먼 이미지인 definite negative {n_j^q}를 판별하는 데에 사용합니다. (실험파트에서 저자는 query image로부터 10m 이내의 image를 potential positive로, 25m 밖 image를 definite negative로 정의했습니다.)

Weakly supervised triplet ranking loss

우리는 place recognition 성능을 최적화할 수 있는 representation \mathbb{f}(\theta)를 학습하고자 하는데 이는 주어진 test query image q에 대해 가까운 이미지(I_{i*})의 순위를 모든 멀리 떨어진 다른 데이터베이스 내의 모든 이미지(I_{i})보다 순위를 높게 매기는 것과 관련 있습니다. (Euclidean distance로 계산)

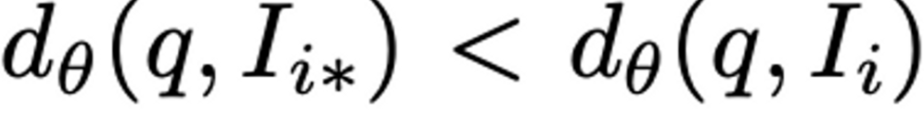
앞에서 언급했듯이 Google Street View Time Machine data에서는 각 쿼리 이미지에 대한 potential positive와 definite negative 튜플 (q, {p_i^q}, {n_j^q})로 구성된 train dataset을 얻게 됩니다. (Google Street View Time Machine 데이터가 제공하는 GPS 정보를 이용해서)

이 potential positive image {p_i^q} 중 query image와 지리적으로 가장 가까운 이미지p_{i*}^q의 수식은 다음과 같습니다.

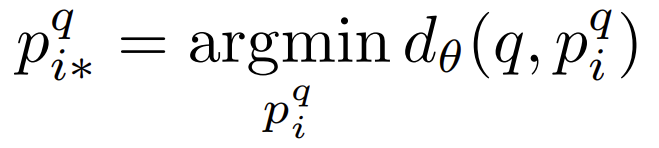
결국 query image와 지리적으로 가장 가까운 이미지 p_{i*}^q 사이 거리가 query image와 모든 negative image와의 거리보다 작아지도록 학습을 해야합니다. 이를 수식으로 표현하면 다음과 같습니다.

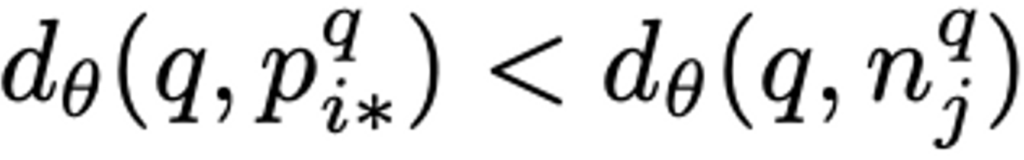
이를 기반으로 저자는 weakly supervised ranking loss를 아래와 같이 정의합니다.

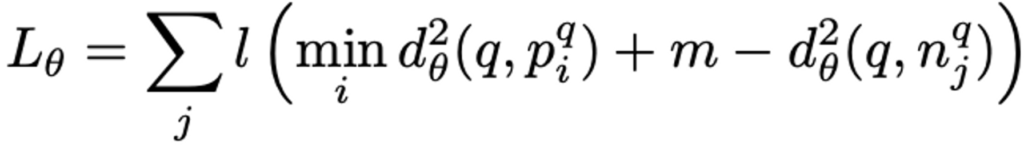
• l(x) = max(x, 0)
• m : margin
• min d_{\theta}^2(q, p_i^q) : query image q와 potential positive image들의 거리 중 가장 짧은 거리
• d_{\theta}^2(q, n_{j*}^q) : query image q와 j번째 definite negative image와의 거리

query image q와 가장 가까운 potential image와의 거리 + margin 값이 query image q와 j번째 negative image 거리보다 작다면 l(x) = max(x, 0)이기에 loss는 0이 됩니다. 즉, query image와 가장 가까운 이미지 거리가 모든 negative image와의 거리보다 작아지는 방향으로 학습하게 되는 것입니다.

Experiments

실험 부분에서는 Pittsburgh, Tokyo 24/7 datasets을 사용했으며, evaluation metric으로는 일반적으로 place recognition 분야에서 사용되는 Recall@N을 사용했습니다. query image에 대한 ground truth position과 25m 이내의 image만을 correctly localized image로 간주합니다.

저자가 제안한 NetVLAD(f_{VLAD}) layer와 더불어 Max Pooling (f_{max}) layer을 사용하였으며, base architecture로는 AlexNet과 VGG-16의 마지막 convolution layer단(conv5)을 crop(fc layer 전부분까지)한 것과 Places205를 사용하였습니다.

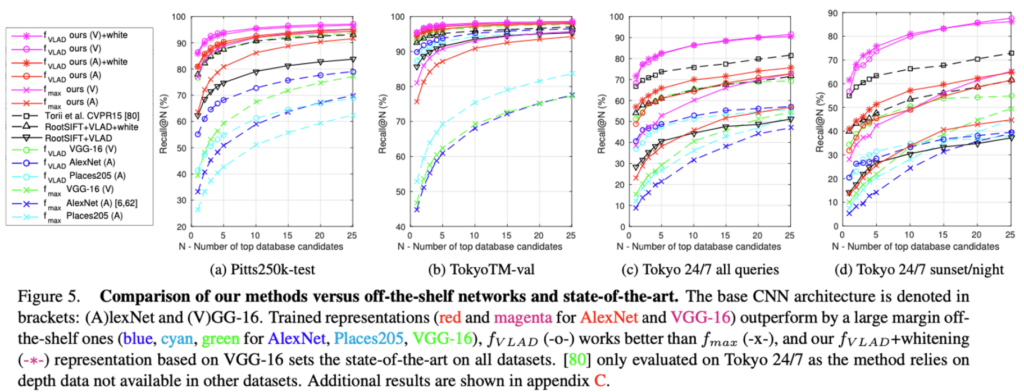
Dimensionality reduction, Comparison with state-of-the-art

실험 결과[Fig 5]를 살펴보면, PCA를 이용하여 4096 Dimension으로 차원 축소를 한 것(-∗-)과 하지 않은 full size vector(-o-)의 성능 차이가 거의 없는 것을 확인할 수 있으며, whitening을 적용한 VGG-16 base의 f_{VLAD}representation(magenta -∗-)가 SOTA를 달성했던 방법론인 Root-SIFT+VLAD+whitening보다 더 좋은 성능을 낸 것을 볼 수 있습니다.

Benefits of end-to-end training for place recognition

Pitts250k-test 에서 NetVLAD aggregation layer를 붙인 AlexNet의 성능은 recall@1이 81%인것에 비해 standard VLAD aggregation을 AlexNet에 적용한 성능은 55%로 47%의 차이가 나는 것을 볼 수 있습니다. 즉 저자가 제안한 방식인 end-task로 학습을 한 representation들이 그렇지 않은 off-the-shelf CNN에 비해 더 좋은 성능을 보여준 것이죠. 이를 통해 2가지를 확인할 수 있는데, (1) 저자가 제안한 방식이 풍부하고도 간결한 image representation을 학습할 수 있다는 것과 (2) 사전학습 된 network인 off-the-shelf은 popular idea지만 object나 scene classification을 위해 훈련된 network이기에 place recognition 분야에서는 적합하지 않다는 것입니다.

which layer should be trained?

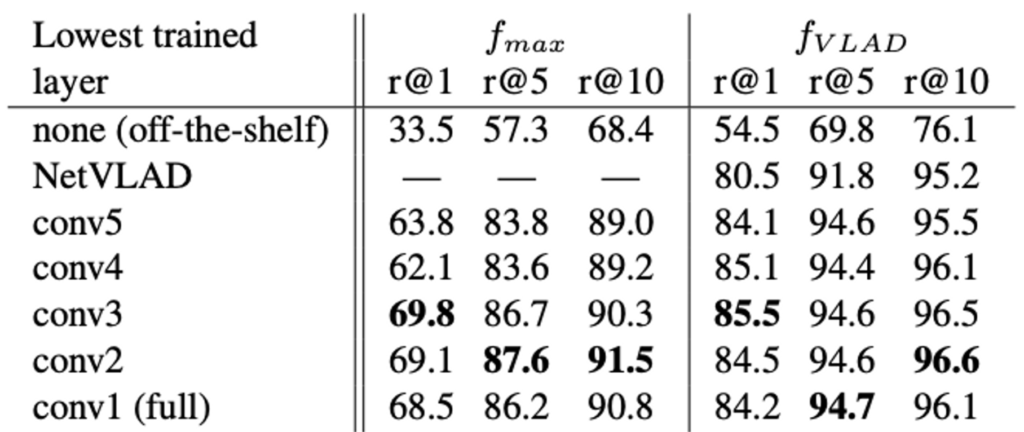
위의 표는 어떤 layer를 학습시켜야 하는지에 관하여 실험한 결과입니다. none (off-the-shelf)와 비교하였을 때 NetVLAD layer만을 학습시키는 것만이 (conv layer는 freeze한 채로) 가장 큰 성능 향상 폭을 보였지만 추가적으로 convolution layer를 학습시키면 성능이 개선되었습니다. 다만 마지막 행인 conv1 (full)을 보면 (conv1만 freeze하고 나머지 layer는 학습) overfitting으로 인해 조금 성능이 떨어지네요.

Qualitative evaluation

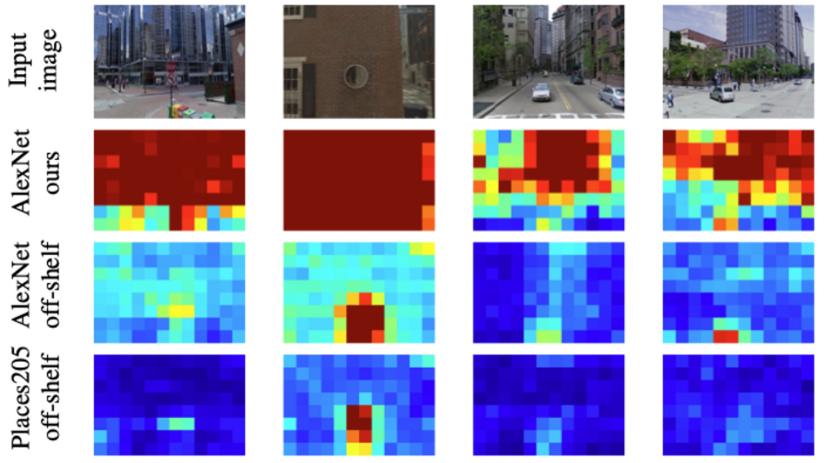
위는 각 모델이 입력 이미지의 어떤 부분에 focus하여 학습을 한 것인지 heatmap으로 시각화한 것입니다. off-the-shelf AlexNet은 ImageNet category인 12가지의 ball type을 구별하기 위해 circular blob과 같은 것에 focus한 것을 볼 수 있다고 합니다. (ball type이 뭔지는 잘 모르겠습니다만 , , ,) 위의 두 결과와 비교하여 저자가 제안한 모델(AlexNet ours)은 자동차나 사람 같은 confusing feature들을 무시하며, building facade와 skyline 등에 focus하고 있습니다.

마지막으로 정성적 결과입니다. 논문에서는 12개 case에 대한 정성적 결과를 담고 있었는데 위 그림의 마지막 열을 제외한 나머지(11개의 결과)는 같은 이미지에 대해 Best baseline은 recognition을 잘 못하고 있는 것에 비해 잘 retrieval한 것을 보입니다. 마지막 열을 보면 전체적으로 어두운 query image이기 때문에 저자가 제안한 방식으로는 어려운 query에 해당한다고 합니다.