이번 리뷰 논문은 저번 리뷰에 이어 diffusion model에 대해 리뷰하고자 합니다. 저번 리뷰에서는 전반적인 흐름을 파악하기 위해 작성했더라면 이번 리뷰에서는 수식도 구체적으로 다뤄볼 예정입니다. 해당 논문에서는 DDPM의 markov chain을 깨뜨려 이전보다 개선된 성능을 보여주는 결과를 보여줍니다.
+ Part 1에서는 수식을 포함한 Diffusion model에 대한 설명까지 다루고, part 2부터 DDIM에 대한 방법론과 실험, 그리고 이후 개선된 몇몇 논문들을 가볍게 다루보도록 하겠습니다.
Intro
이전 리뷰에서 다룬 DDPM에서는 수식을 최대한 생략하여 전반적인 흐름에 대해서만 다뤄보았습니다. 이번 리뷰에서는 수식들도 함께 다뤄보면서 구체적인 흐름을 파악해보겠습니다. 본격적인 설명을 들어가기에 앞서 전반적인 파이프라인에 대해 설명하도록 하겠습니다.
Overview
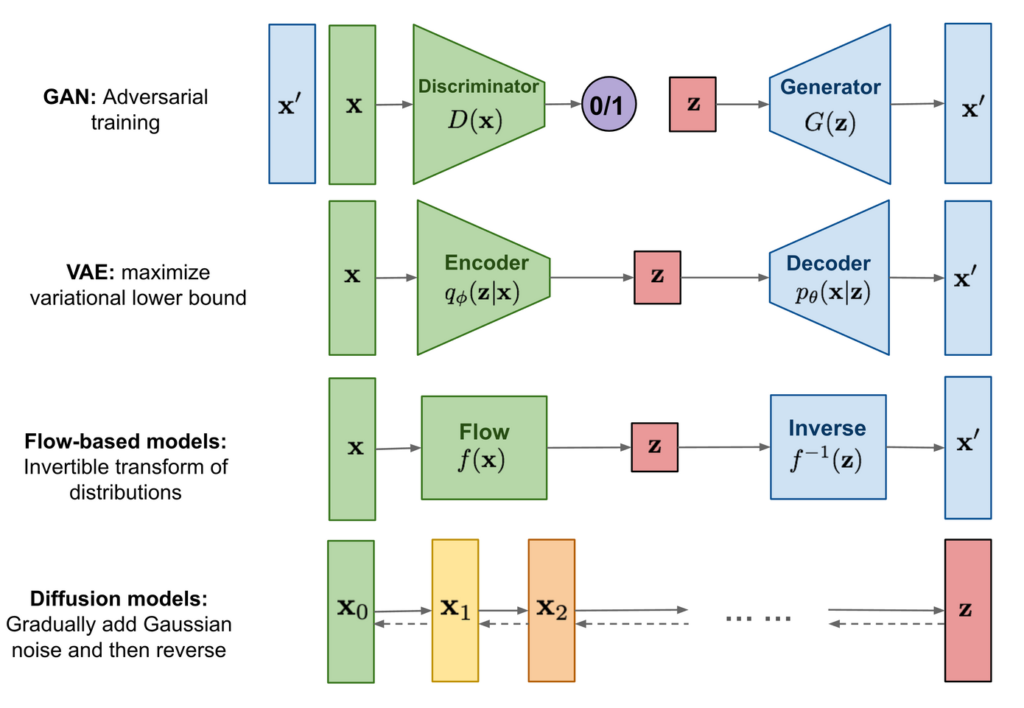
Diffusion model은 encoder를 통해 latent feature (~= vector)를 구하고, decoder를 통해 영상을 생성하던 이전 생성 모델의 흐름과는 많이 다른 파이프라인을 가집니다. Diffusion model은 크게 2가지 프로세스로 구성됩니다. 가장 먼저 입력 데이터에 반복적으로 가우시안 노이즈를 가해 다루기 쉬운 확률 분포 변환하는 forward와 가해진 노이즈를 예측하여 노이즈 영상을 복원하는 reverse 과정으로 구성됩니다.
이전 리뷰의 질문을 보니 많은 분들이 딥러닝 모델이 어디에 어떻게 구성되는지 헷갈리시는 분들이 많으신 것 같습니다. 딥러닝 모델은 reverse에서 사용되며, forward에서는 가우시안 노이즈를 가하는 수학 모델만 사용됩니다. 그리고 reverse에서 반복적으로 노이즈를 복원한다는 뜻은 말 그대로 딥러닝 모델을 이용해 노이즈 복원을 T번 반복한다는 뜻입니다. 해당 딥러닝 모델의 입력은 영상 데이터이며, 출력 데이터는 영상과 동일한 크기를 가진 데이터가 출력됩니다. 그렇기에 U-Net처럼 입력과 출력의 크기가 동일하도록 복원하는 모델이 사용 되어집니다. 또한, 스텝 마다 개별적인 모델을 사용하는 것이 아니라 동일한 모델을 사용합니다. (+모델의 입력에는 몇 번째인지에 대한 정보도 같이 들어간다고 하는데… DDPM 논문에서 그런 내용을 찾지 못해서 작성하진 않았습니다.)
오늘은 forward와 reverse 과정과 수학적 증명에 대해 다루면서, 해당 논문이 DDPM의 어떤 부분을 개선시켰는지에 대해 설명하고자 합니다.
Forward diffusion process
실제 데이터의 분포 \mathbf{x}_0 \sim q(\mathbf{x}) 중 샘플 데이터 x_0 가 있을 때, 해당 데이터에 작은 양의 가우시안 노이즈를 T steps을 가하는 것이 forward process라고 합니다. 해당 process를 통해 노이즈 샘플 \mathbf{x}_1, \dots, \mathbf{x}_T 가 생성 됩니다. 해당 step은 variance schedule {\beta_t \in (0, 1)}_{t=1}^T 를 통해 조절됩니다. 이를 Markov chain에 따라 정의하자면 아래와 같습니다.
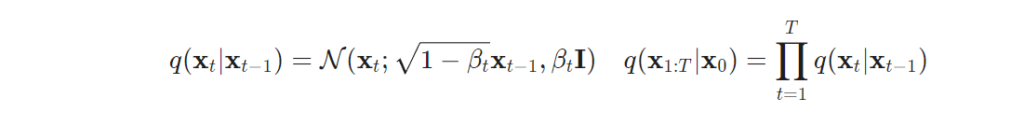
데이터 샘플 x_0 은 step t가 커질 수록 데이터 정보를 소실하며, 최종적으로 T->inf에 도달하였을 때, isotropic Gaussian distribution와 동일한 분포를 가지게 됩니다.
+ 가우시안 분포를 따르게 하는 이유는 복잡한 영상 데이터를 정규화된 분포~조작하기 쉬운 분포로 만드는 것이라고 보시면 됩니다. 해당 포인트가 Generative model의 특징에 해당합니다. Discriminate model인 GAN을 diversity가 떨어지는 이유도 각 데이터 별 추론되는 feature의 분포의 특성을 알 수 없기 때문이라고 볼 수 있습니다.
어떠한 step t에서의 샘플 x_t 를 깔끔하게 정의하기 위해 reparmaeterization trick으로 \alpha_t = 1 - \beta_t와 \bar{\alpha}_<em>t = \prod_</em>{i=1}^t \alpha_i 를 적용했을 때 아래와 같습니다.
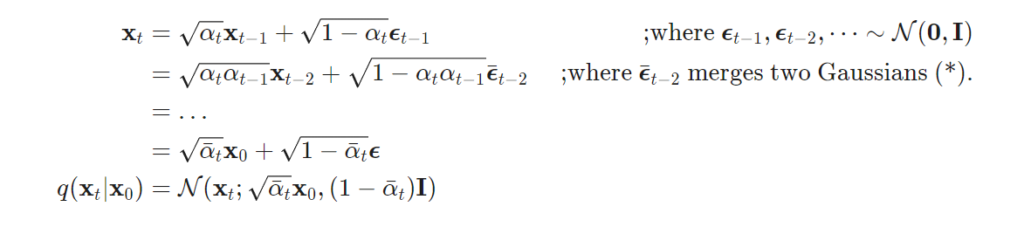
+ 두 서로 다른 분산은 합의 법칙에 따라 Var(a) + Var(b) = Var(a+b)로 변환이 가능합니다. 위의 수식은 분산의 합의 법칙에 따라 t를 t-1로 대입하면서 수식을 정리한 결과입니다.
위의 정리에 따라 노이즈 영상을 아주 쉽게 만들 수 있게 됩니다. 한번 더 정리하자면 Markov chain rule에 따라 step t에서의 노이즈 영상 x_t 는 원본 샘플 데이터 x_0 와 사전 정의된 variance schedule \beta 를 이용하여 쉽게 생성 할 수 있게 됩니다.
Reverse diffusion process
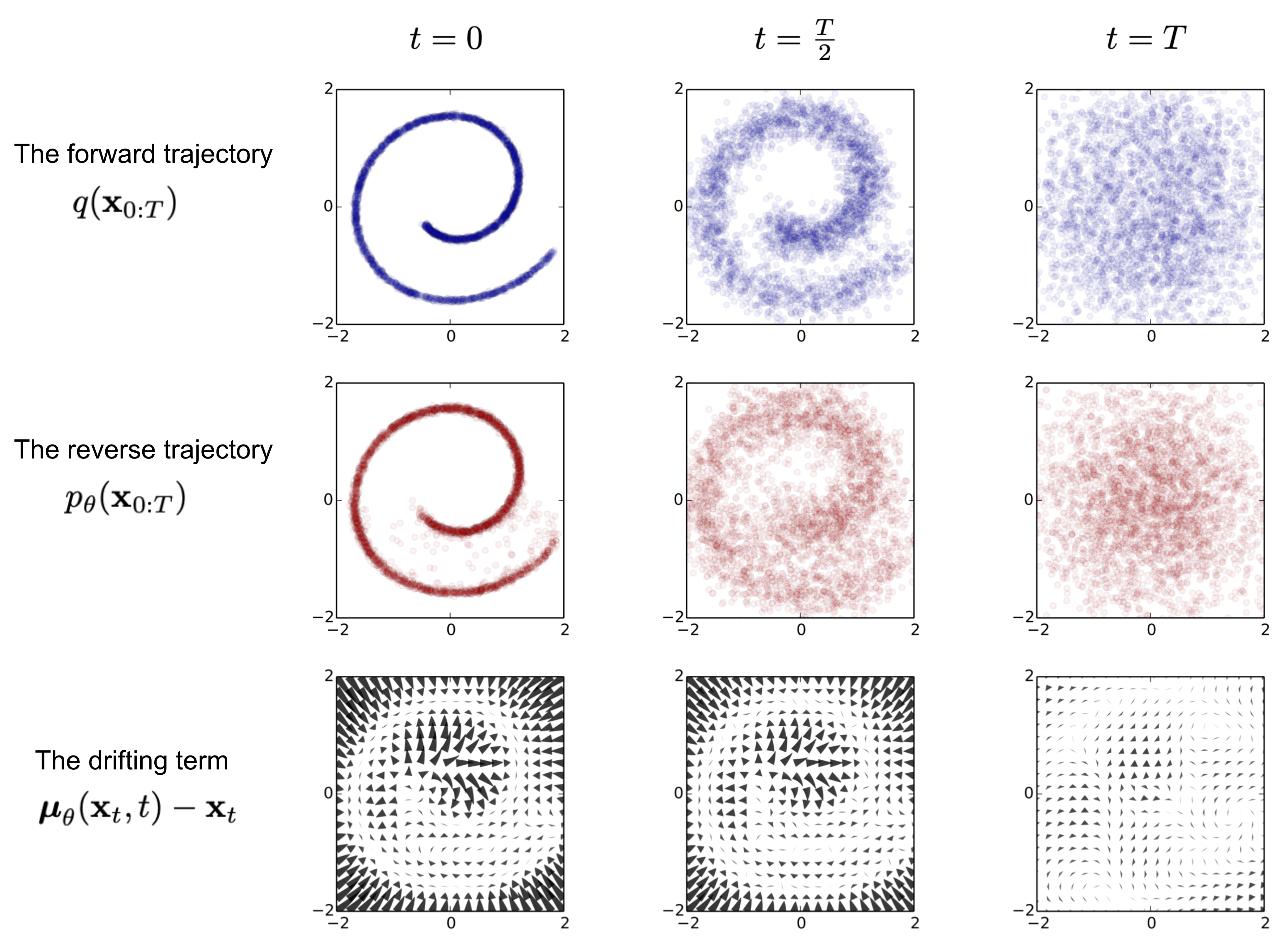
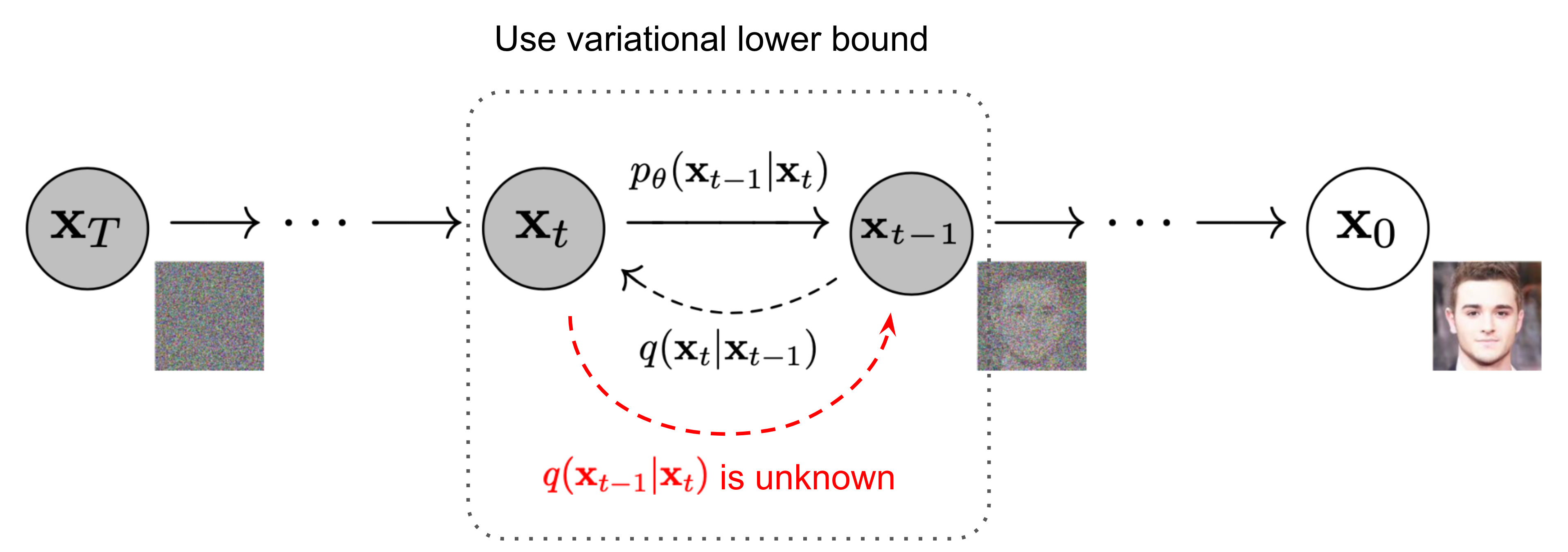
Reverse process는 forward process에서 가우시안 노이즈를 가해 생성된 \mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) 를 역으로 복원하는 조건부 확률 q(\mathbf{x}_{t-1} \vert \mathbf{x}_t) 을 찾아낸 는 것이 목표입니다. 하지만 가우시안 정규 분포로부터 원하는 데이터로 복원하는 것은 매우 어려운 일이기에 학습 가능한 모델 p_\theta 를 이용합니다. 이를 간단하게 정의하면 다음과 같습니다.
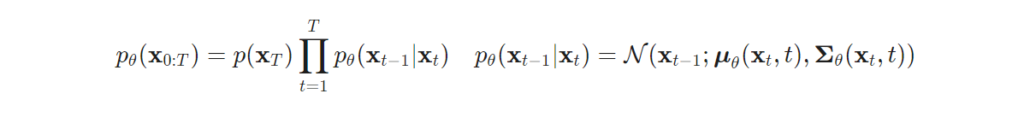
위의 수식에 우리가 알고 있는 데이터 x_0 를 고려한 조건부 확률에 대한 bayes’ rule로 정리하자면 다음과 같습니다.
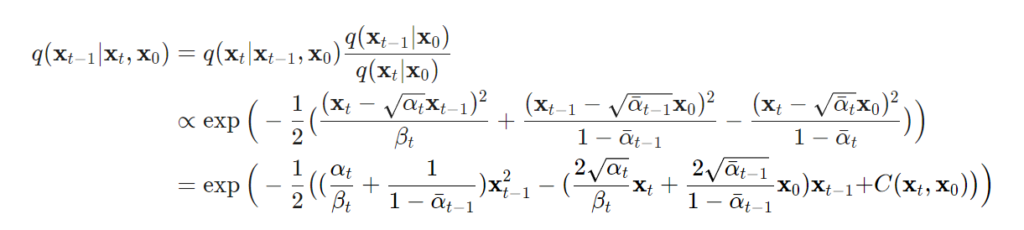
위 수식으로 정리된 식에 대한 평균과 분산을 정리하면 다음과 같습니다.
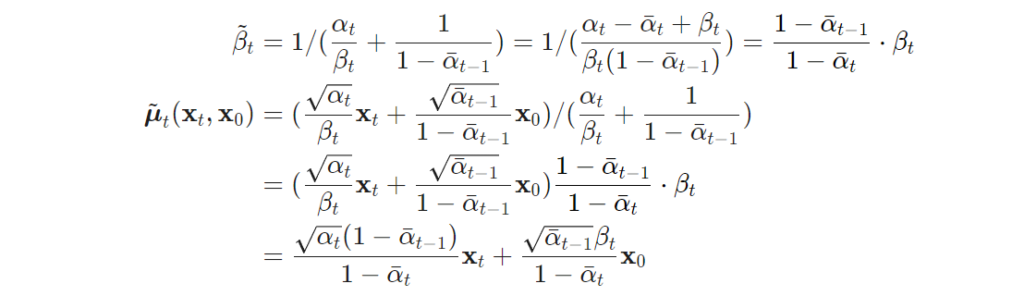
위의 수식에서 정의된 분산을 \mathbf{x}_0 = \frac{1}{\sqrt{\bar{\alpha}_t}}(\mathbf{x}_t - \sqrt{1 - \bar{\alpha}_t}\boldsymbol{\epsilon}_t) 에 의해 정리하자면 다음과 같은 수식으로 정리 할 수 있습니다.
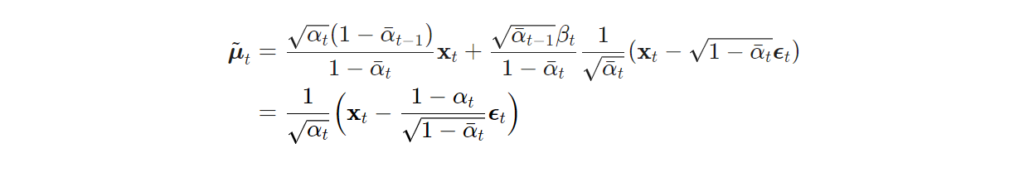
Diffusiom model은 평균과 분산을 이용하며 노이즈를 가한 영상으로부터 학습을 한다는 점에 있어 VAE와 상당히 유사한 모습을 보여줍니다. 분산과 평균을 학습하기 위해 VAE와 동일하게 ELBO를 고려한 variational lower bound to optimize the negative log-likelihood 이용합니다. 이에 대한 수식은 아래와 같습니다.
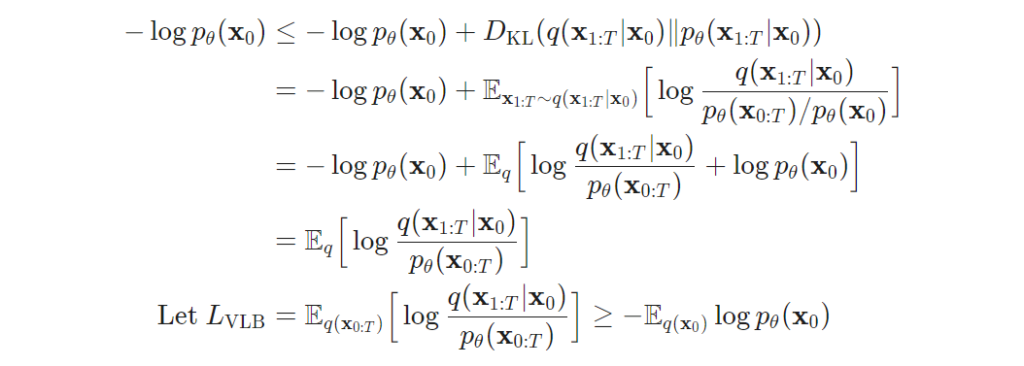
자, 그럼 이제 위의 수식을 간략하게 정의하며 KL-divergence로 재정의하자면 다음과 같습니다.

위의 수식에서 variational lower bound loss의 각항에 대해 정리하면 다음과 같습니다.
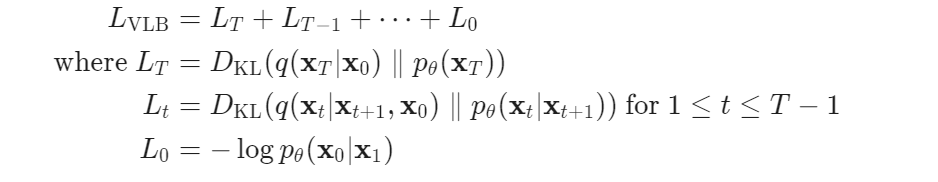
위의 텀에서 L_0를 제외하고는 남은 텀들은 두 분포를 비교하며 학습을 진행합니다. 이 중 L_T 는 상수로 학습 중 무시하고 사용해도 됩니다. 이는 q는 애초에 학습 파라미터가 아니기도 하며, x_T는 가우시안 노이즈로 정의했기 때문입니다.
위에서는 학습을 위한 loss를 정의했으니 그럼 본격적으로 reverse process를 학습 시키기 위해 텀을 정리하고자 합니다. reverse process는 영상 정보를 복원하기 위해 조건부 확률 p_\theta(\mathbf{x}{t-1} \vert \mathbf{x}_t) = \mathcal{N}(\mathbf{x}{t-1}; \boldsymbol{\mu}\theta(\mathbf{x}t, t), \boldsymbol{\Sigma}\theta(\mathbf{x}_t, t)) [/latex]로부터 \boldsymbol{\mu}</em>\theta 를 학습시켜 \tilde{\boldsymbol{\mu}}_t = \frac{1}{\sqrt{\alpha_t}} \Big( \mathbf{x}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \boldsymbol{\epsilon}_t \Big) 를 예측을 목표로 합니다. 많은 diffusion model에서는 직접적으로 평균을 예측하는 것이 아니라 forward에서 생성된 noise \boldsymbol{\epsilon}_t 를 예측하는 방식으로 학습함으로써, 조금더 명확한 cue를 이용하여 학습이 가능해집니다. 이에 대한 수식은 다음과 같습니다.
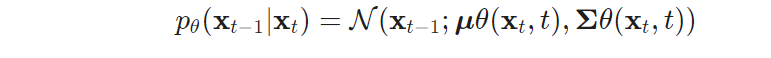
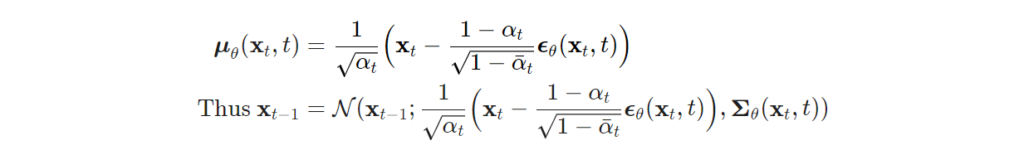
위에서 정의된 loss 텀 중 평균에 대해 정의된 텀을 noise로 정리하면 다음과 같이 정의 됩니다.
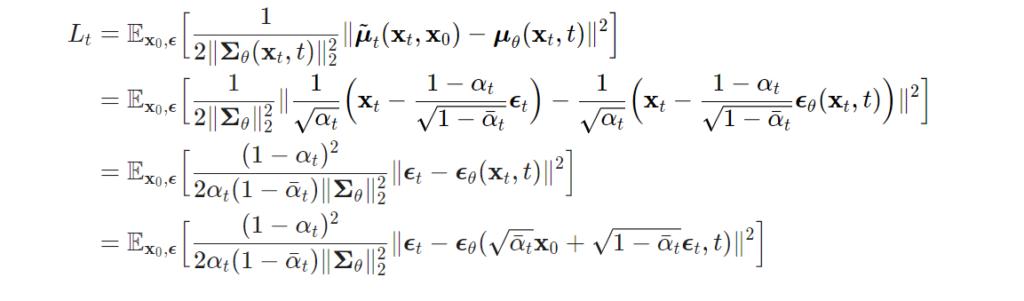
여기까지가 diffusion model에 대한 기본 이론과 수식을 다뤄보았습니다. 이후 diffuison model들은 해당 이론과 수식을 기본으로 개선 방법을 제안하는 방향으로 방법론을 풀어나갑니다. 추후 diffsuioon model 기반의 방법론들을 보실 일이 있으시다면 해당 리뷰를 참고하시면 좋을 것 같습니다. 이후 리뷰에서는 DDIM과 이외의 개선 논문들을 다뤄보도록 하겠습니다.