[NeurIPS 2022 Invited Talks] The Forward-Forward Algorithm: Some Preliminary Investigations

안녕하세요. 열 번째 X-Review입니다. 지난 4월 간의 일정을 마친 후 5월에 들어서며 오랜만에 작성하는 X-Review입니다. 다음 주부터 현재 주 관심 분야인 Small-object detection과 관련된 실험을 이어나가기 이전에, 예전 페이스북 Pytorch KR에서 지나치며 본 후 관심이 생겨 나중에 읽어봐야지 했던 논문을 리뷰하도록 하겠습니다.

우선 해당 논문을 한 줄로 요약하자면, “딥러닝에 역전파 (Backpropagation)를 고안한 제프리 힌튼 교수님의 논문으로, 실제 대뇌 피질의 학습 방법에 역전파 과정이 있을까에 대한 의구심에서 시작한 순전파만으로 학습하는 딥러닝 방식입니다. 아래의 리뷰를 읽다보면 저와 같은 느낌을 받으실 수도 있겠지만, 해당 논문에서 제안하는 방식이 Backpropagation은 허상이였다! 이제 그렇게는 딥러닝을 학습하지 말자!는 말이 아닌, 앞으로 Forward-Forward Algorithm (앞으로는 FF 알고리즘이라 명하겠습니다)이 딥러닝의 새로운 학습 토템으로 자리 잡을 수 있지 않을까 하는 하나의 견해이니, 이 점 참고하시면서 리뷰 읽어주시면 감사하겠습니다. 힌튼의 논문은 처음 읽는 것 같네요. 리뷰 시작하겠습니다.

1 What is wrong with backpropagation

딥러닝의 발전 속 2 번의 겨울이 도래했었으며, 그 중 첫 번째 겨울은 XOR 문제와 결부되어 있다는 사실은 모두들 알고 있을 것입니다. 이를 해결한 것이 Backpropagation, 역전파이며 이를 고안해 낸 사람이 바로 이번 논문의 저자, Geoffrey Hinton 교수님입니다. 물론 이전 Paul Werbos가 Backpropagation을 제안했지만, 주목을 받지 못했으며 현재 우리가 알고 있는 Backpropagation은 제프리 힌튼 교수님이 고안해 낸 방법입니다. 논문의 시작은 지난 몇 십년 간의 딥러닝의 발달과 성공의 뒤에는 방대한 데이터의 파라미터를 조절하여 Gradient를 조절하는 방식 (SGD)이 있으며, Gradient는 주로 Backpropagation을 사용하여 계산되어 왔습니다. Backpropagation 등장 이후, 학자들은 뇌의 작동 방식에 관심을 갖기 보다 Backpropagation을 사용하여 인공 지능의 성능을 높이는 것에 관심을 가져왔습니다. 누구든 알고 있을 지식인데 이 문단을 가져온 이유는, 해당 문장을 읽다보니 하나의 생각이 들었기 때문입니다. 인공지능은 결국 컴퓨터가 사람의 지각, 사고 방식을 모사하는 일련의 과정인데, 정작 현재는 그 본질을 생각지 않은 채 성능을 올리는 방법만 고민하는 것은 아닐까 생각이 들었습니다.

힌튼이 문제로 삼은 점은 다음과 같습니다. 대뇌 피질의 학습 과정에서 실제로 Backpropagation 방법이 사용되는가? 즉, 실제로 우리 뇌는 오차를 역으로 전파하여 오차를 수정하는 과정이 있는지 미심쩍다고 하며, 역전파가 있다면 이전의 신경 활동 값을 모두 저장해야하나, 실제로 그런지에 대해서도 의구심이 든다고 말합니다.

우리는 이를 이해하기 위해 인간이 정보를 학습하는 메커니즘에 대해 담은 피아제의 인지 발달 이론을 들고와서 설명할 필요가 있습니다. 이번 리뷰에서 해당 논문을 자세히 알아보고자 함은 아니라, 인간이 실제로 물체를 지각하고 인지하는 과정에 대해 훑기 위함이며 다음의 링크에서는 자세한 내용을 읽을 수 있습니다. 인지 발달 이론에서 핵심은 인간이 본인이 모르거나 새로 알게된 사실을 받아들이는 과정에서 본인의 인식 (뉴런의 Weight로 이해하면 됩니다)이 잘못된 결과에 대해 오차를 통해 다시 적용하는 과정이 명시적으로 존재하지 않으며, 정보 제공자를 통해 지식 체계가 강화되고 이전의 지식과 동화됩니다. 힌튼은 이에 그치지 않고 피질의 학습 과정에 대해 다시끔 살펴보며, 아래의 그림을 통해 다시 살펴보겠습니다.

마치 Nature의 논문 리뷰 같습니다만.. 시각 정보를 처리하는 피질 (Visual Cortex)의 연결된 구조는 Top-down (Forwardpropagation)으로 구성되어 있으며, 만약 Backpropagation에 해당하는 Bottom-up 과정이 존재한다면 피질로 부터 시각 정보를 받아들이는 망막 이전 시신경까지 오차가 전파되는 과정이 있어야하는데, 실제로는 그렇지 않다는 것 입니다. 시각 정보는 마치 일종의 동영상을 전달받는 것과 같이 연속적인 프레임으로, 오차 전파를 위한 추가적인 Time-out이 존재하지는 않는다고 합니다. 피아제의 인지 발달 이론으로 설명하면 우리가 이미지를 보고 있다면, 시각 피질은 이미지에 대한 정보를 수정하는 것으로 보입니다. 즉, 이미지를 보면서 해당 지점에서 일종의 Loop를 통해 정보 체계를 수정하는 것과 같은 의미입니다.

또한 힌튼은 만약 Backpropagation이 존재한다면 윗 문단에서 말한 것과 같이 인식체계에 주기적인 Time-out이 존재해야한다고 주장합니다. 역전파가 일어나는 동안, 파이프라인 뒷쪽의 정보가 앞쪽으로 전해져야하는데, 인식은 연속적이기 때문에 이를 위한 Time-out이 존재하지 않습니다. 마치 Online-learning처럼, 이미지가 인식될때마다 학습된다는 의미입니다.

또한 힌튼이 의심한, 그렇다면 Backpropagation이 일어나기 위해 필수적인, 뇌가 이전의 정보를 기억하고 있는가에 대해 Unknown Blackbox Block이 존재하는 경우엔 설명이 안된다는 점입니다. 또한 역전파 계산을 위해서는 뉴런의 모든 지점이 마치 미분 가능한, 도함수의 형태를 가지고 있어야하는데 이러한 부분도 불명확하다는 점입니다.

위의 그림을 통해 다시 살펴보면, Blackbox에 대해 FF 알고리즘은 적용할 수 있지만, Backpropagation에 대해서는 완벽한 정보를 가지고 있지 않기 때문에 연산이 불가능합니다. 힌튼은 이 점에 대해 강화학습이 해결할 수 있지 않겠냐는 반론에 대해 미리 준비한 듯 강화학습과, 그에 대한 단점을 언급합니다.

강화학습에 대한 지식이 없어 해당 부분에 대해 명확한 설명을 드리기는 어려우나, 강화학습은 뉴런의 활동에 대해 weight의 일부에 랜덤한 변화를 주어, 변화에 따라 바뀌는 결과에 대한 보상을 해주는 방식이라고 합니다. 강화학습에서 에이전트는 보상을 최대화하는 방식으로 학습합니다. 예를 들어 게임에서 이긴 경우 양의 보상을, 진 경우 음의 보상을 통해 보상을 최대화하려는 방향으로 행동을 선택하고 보상이 높은 전략을 취하게 하는게 강화학습의 전략입니다. 따라서 강화학습은 Blackbox에 상관없이 Forwardpropagation이 가능하다고 볼 수 있습니다.

하지만 힌튼은 강화학습 방식에 대해, 해당 방식은 Variance, 즉 경우의 수가 굉장히 높기 때문에 각 Parameter의 변화가 output에 미치는 영향을 확인하기 어렵다고 합니다. 이를 위해 Parameter의 수에 반비례하게 learning rate를 설정하는 방식도 존재하지만, Parameter의 수가 늘어날 수록 학습 속도가 느려져 이점이 사라집니다.

힌튼은 FF (Forward-Forward) 알고리즘의 장점으로 ReLU와 같은 비선형성을 포함하지 않는 네트워크도 학습할 수 있으며 (Backpropagation의 부재에서 오는 이점으로 보입니다) 연속적인 데이터에 대해 학습의 Pipeline이 지속된다는 장점이 있다고 주장합니다. 하지만 어떤 때는 (특히 대용량 데이터에 대해) Backpropagation보다 느리며 아직은 Generalized 되지 않아 전력 문제가 되지 않는 한 (Backpropagation을 통한 딥러닝 모델의 학습은 많은 GPU와 전력을 필요로 하기에) 아직은 Backpropagation 알고리즘을 통한 학습 방법을 능가하긴 어려울 것으로 보인다고 말합니다. 즉, FF 알고리즘은 그 자체로 Backpropagation을 이길만큼 성능면에서 혁신적이라고 볼 수는 없으나, 딥러닝 학습의 새로운 지평선을 열어준 것으로 보입니다. 그럼, 이제 FF 알고리즘에 대해 알아보겠습니다. 사실 그 아이디어는 굉장히 간단합니다.

2 The Forward-Forward Algorithm

기본적으로 딥러닝 모델, MLP 구조에서 각 레이어는 입력 정보가 상이하기 때문에 출력 Feature 또한 상이하다는 것이 전제되어 있습니다. 즉, 데이터의 분포가 다르므로 레이어에서의 Representation이 다릅니다. 이를 다른 시각으로 보면 각 레이어에서의 독립적인 Task를 구하는 과정, 즉 Greedy 알고리즘으로 생각할 수 있습니다. 그러므로 FF 알고리즘은 모든 레이어를 독립적으로 학습한다고 가정합니다.

해당 가정을 토대로, FF 알고리즘은 서로 반대되는 Object function을 갖는 두 데이터가 각각 Forward 되면서 역전파를 대체할 수 있는데, 이 때 두 Forward Pass를 Positive Pass와 Negative Pass라고 명합니다. Possitive Pass는 Real (Positive) 데이터에 적용되며, 각 레이어의 Weight이 goodness를 증가하는 방향으로 작용합니다. 이 때 말하는 goodness는 한국어로 번역이 꽤 어려운데, 쉽게는 최적의 선택을 한다고 생각하면 될 것 같습니다. 반대로 Negative Pass는 Negative 데이터에 적용되어 각 레이어의 Weight이 goodness를 감소하는 방향으로 작용합니다.

위의 작동 과정을 풀어 설명하자면, 마치 Contrastive learning과 같이 Positive Pass는 Positive 데이터에 가까워지며 동시에 Negative Pass와는 멀어지게끔, 반대로 Negative Pass는 Negative 데이터에 가까워지며 (실제로는 Positive 데이터에 멀어진다고만 해석하는 것이 더 옳은 것 같습니다만) Positive 데이터에 멀어지는 방향으로 작용한다고 볼 수 있습니다. 그렇다면 이 때 말하는 goodness는 어떻게 구해질까요? 힌튼은 단순히 Squared Sum을 통해 구합니다. 힌튼은 이에 대해 각주로 미분이 쉬움과 동시에 Layer normalization이 goodness의 과정에서 제거되기 때문이라고 합니다. 뒤의 이야기에 대해서는 정확한 설명은 없지만, 뒤의 Layer normalization이 나올 때 다시 추정해보겠습니다.

이제 아래의 그림을 통해 살펴보겠습니다. 아래 그림에서 왼쪽은 Real (Positive)데이터로, 우리는 이 때 goodness를 증가시키는 방향으로 작용해야합니다. 따라서 레이어의 신경망 활동을 통한 Output인 a_j^l 들의 Squared Sum이 되며, 반대로 오른쪽의 Negative Pass는 Negative 데이터에 대해 goodness를 감소시키는 방향으로 작용하니 a_j^l의 Negative Squared Sum으로 goodness를 감소시킵니다.

사실 본 논문은 해당 아이디어가 전부입니다. 물론 아래에서 디테일한 부분에 대해 조금 더 짚겠지만, 핵심적으로 알아야할 점은 Forward Pass에서 일종의 Loop를 돌며 마치 contrastive learning과 같이 Positive / Negative Pass가 goodness를 각각 증가시키는, 감소시키는 방향으로 작용하며 인지과정을 통한다는 점입니다. 디테일한 부분은 아래 논문의 수식을 통해 다시 살펴보겠습니다.

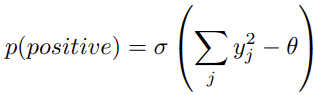
위의 수식은 특정 레이어 노드의 인덱스 j에 대해 Positive sample일 확률을 구하는 수식으로, p(negative)는 해당 수식의 음의 부호를 붙인 것과 같습니다. 이 점을 유념한 채 위의 수식을 살펴보면, 각 레이어는 Positive / Negative Pass에 따라 Positive input에 대해서 Negative input을 기준으로 특정 Threshold만큼 높이는 것을 목적으로 합니다. 이 말이 조금 어렵게 다가올 수 있는데, Threshold는 Positive와 Negative를 구별해낼 수 있도록 만드는 일종의 기준선과 같이 쓰이며, Positive 데이터는 Threshold 보다 높게, Negative 데이터는 Threshold 보다 낮게 goodness가 형성됩니다. 물론 아직도 이해가 어려울 수 있으나, 더욱 중점적으로 고민할 수 있는 부분은 역전파는 Output에서만 Objective function을 가지고 이를 통해 Weight을 조절해나갔는데, FF 알고리즘은 각 레이어마다 Objective function을 가지는 것을 알 수 있습니다.

사실 본 논문을 읽을 때 1장과 2장에서만 반나절을 투자할만큼 개념이 어려웠는데, 이해가 되었다 생각이 들었을 때 작성했는데도 말로 풀다보니 다시 어려운 것 같네요.. 후에 준비가 된다면 세미나 시간에서 다시 살펴보도록 하겠습니다.

2.1 Learning multiple layers of representation with a simple layer-wise goodness function

결국 우리는 단일 레이어에 대해 각 데이터에 대한 goodness, 최적의 선택을 구하는 방식을 알게 되었습니다. 다만, 첫 번째 레이어의 Output이 그대로 두 번째 레이어의 Input으로 전해진다면, 하나의 문제점이 있을 수 있습니다. 이는 우리가 하나의 레이어에서 이미 Squared Sum을 통해 goodness로 Positive / Negative 데이터를 구별할 수 있게끔 학습했기 때문에, 두 레이어의 Output vector의 크기만으로 구별될 수 있다는 점입니다. 이는 코드 상으로 살펴봐야될 것 같긴 합니다만, 어쨋든 두 Output vector의 크기가 다르다면 두 번째 레이어부터는 새로운 Representation을 가질 수 없게 됩니다. 이는 자명합니다. 두 번째 레이어에서부터 새로운 Representation을 기대하기 위해선 Output Feature Vector의 크기를 다음 레이어의 Input으로 사용하기 이전에 Normalize해주면 됩니다. 방향 정보만 전달해주려는 목적이죠. 이렇게하면 첫 번째 레이어에서 goodness를 계산하기 위해 사용했던 정보들이 제거되는 것 처럼 보이지만, Orientation, 즉 방향은 전달하기 때문에 Relative activity, 연관성 있는 활동은 이어나갈 수 있다고 합니다. 이 때의 Normalization은 이전 레이어의 Mean을 빼지 않은 채 진행하였습니다.

3 Some experimnets with FF

이전 문단에서 대뇌 피질의 학습 과정부터 FF 알고리즘의 소개까지 꽤나 긴 시간을 보냈는데, 역시 실험이 중요한 것처럼 보입니다. 비지도학습과 지도학습에 대해 진행하며 실험이 이어지다 뒷편의 6절부터는 볼츠만 머신과의 차이부터 GAN과의 연관성, Contrastive learning과의 관계 등 꽤나 많은 부분에 대해 언급하지만, 이번 리뷰에서는 MNIST 데이터 셋을 토대로하는 비지도학습과 지도학습에 대한 실험을 살펴보고 리뷰를 마치겠습니다. 후에 기회가 된다면 2편으로 다른 내용에 대해 다루고 싶지만, 볼츠만 머신 등의 다른 부분에서 제가 아직 이름만 들어봤던 방법 혹은 알고리즘이라.. 리뷰에 풀기에는 오히려 혼선을 줄 것 같아 지양하겠습니다.

힌튼은 MNIST 데이터 셋이 FF 알고리즘의 Feasibility를 보이는 좋은 예시라고 보인다고합니다. CNN은 MNIST 데이터 셋에 대해 0.5-0.6%의 오차를 보이며 MLP는 약 1.4%의 오차를 보입니다.

실험 이전에, 힌튼은 FF 알고리즘의 두 의문점에 대해 설명합니다. 우선, Negative 데이터를 학습하는 goodness가 어떠한 효과를 가져오는지, 두 번째로는 Negative data를 어떻게 만들어내는지입니다. 힌튼은 해당 의문점에 대해 설명하고자 Hand-crafted Negative data를 생성합니다. Self-supervised learning 의 주된 학습 방법인 Contrastive learning (위에서 계속 해당 FF 알고리즘이 마치 Contrastive learning과 같다고 설명했습니다)를 Supervised learning에 활용할 때는 입력 Input vector를 Representation vector로 바꾸어 이를 label에 대한 Confidence score (Probability)를 구하는 Linear transformation으로 학습하는 구조를 활용합니다. 이러한 과정은 Hidden layer가 없이 학습되므로 Backpropagation이 따로 필요하지 않으며, FF 또한 이러한 관점에서 Positive Sample과 Negative Sample을 활용한 Representation learning을 진행합니다.

이 때 FF 알고리즘이 이미지의 전반적인 부분 (long-range correlation)을 학습하기 위해서는 Negative dataset이 Positive dataset과 이미지가 전반적으로는 다르나, 부분적으로는 유사하게 구성하는 것이 중요합니다. 이렇게 해야만 각 레이어가 이미지의 전반적인 부분에 집중하기 때문입니다. 이는 당연하게도, 레이어는 Short-range correlation에 대해서는 Positive/Negative를 구별하기엔 굉장히 어렵기 때문입니다. 이를 위해 힌튼은 1/0으로 구성된 마스크를 넓게 구성한 다음, Real 데이터를 마스크와 마스크의 1/0을 반대로 뒤집은 마스크를 적용하여 합한 데이터를 테이터 셋으로 구성합니다. 아래 그림을 살펴보면 좋을 것 같습니다.

이제 Negative Sample을 생성한 채, 4개의 레이어를 갖는 MLP를 학습한 결과 1.37%의 오차를 보였다고 합니다. 실제로 Label을 예측할 때는 뒷단의 세 레이어의 Normalized Output Vector를 사용했다고 합니다.

다음은 Supervised learning입니다. FF 알고리즘은 오차를 역전파하는 과정이 없기 때문에, Supervised learning을 위해서는 Input에 Label을 추가하는 방식으로 구현합니다. 이번에는 Label이 옳다면 Positive, 틀리다면 Negative 데이터가 됩니다. 이 때 중요한 점은 Positive / Negative를 구별짓는 것이 오직 label이므로, FF 알고리즘에서 Negative 데이터로 판명된 Representation (Feature)은 Prediction 시 모두 무시하게끔 학습해야한다는 점 입니다. 힌튼은 앞선 Unsupervised learning에서와 동일한 MLP 구조를 학습시켰을 때, 1.36%의 오차가 나타났다고 합니다.

결국 두 방법 모두 현재 Backpropagation을 사용한 CNN 구조보다 오차가 높다는 점은 존재하지만, 힌튼이 말하고 싶은 점은 특정 Label과 이미지만을 입력으로 넣은 후, 각 레이어의 Activation 결과로 축적된 goodness를 통해 가장 높은 goodness를 갖는 Label을 예측값으로 두면 되는, 간단하면서도 직관적인 구조이며 이것이 정말로 뇌가 이미지를 인지하고 학습하는 과정임을 시사합니다. 현재는 Positive Pass와 Negative Pass가 Squared Sum으로 단순히 구현되어 있는데, 이를 발전시키면 더 좋은 결과를 보이지 않을까하는 사견이 듭니다.

리뷰를 마치려 했으나 그래도 실험 테이블 하나쯤 가져오고자, CIFAR-10 데이터셋에서의 실험을 보겠습니다. 현재 CIFAR-10은 50,000 장 분량의 32x32 크기의 RGB 이미지로 구성되어 있으며, Object와 Background 등 정보가 다양하므로 앞선 MNIST 때와 같은 방법으로는 학습이 진행기 힘들 것으로 보입니다. FF 알고리즘에서 가장 중요한 점은 CNN과 달리 레이어 간의 Weight가 공유되지 않는다는 점으로, 따라서 힌튼은 2-3개의 Hidden Layer를 가질 때 한 레이어에서 3072 개의 노드를 갖도록 구성했습니다. 3072라함은 결국 32 x 32 x 3이므로, 각 Hidden layer에서 Output으로 나오는 텐서의 차원을 모두 곱한 값에 해당합니다. 이 때 연산이 되는 Hidden unit은 11x11의 Receptive Field를 갖고, 각 노드에서 Input의 크기는 11 x 11 x 3입니다. 이 부분이 굉장히 직관적이면서.. 이해하기에 쉽지 않았네요. 아래 표를 살펴보겠습니다.

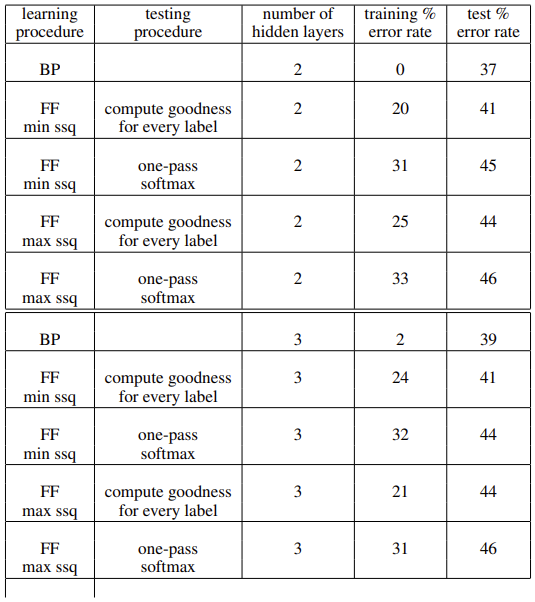
학습 구조를 동일하게 한 채 Backpropagation (BP)와 FF 알고리즘에서의 에러를 비교한 결과입니다. 실험에서 살펴볼만한 점으로는 FF가 BP 방식에 대해 크게 뒤쳐지지는 않으면서도, BP가 traning error를 보면 모델이 Fitting되는 속도가 더욱 빠른 것을 알 수 있습니다. 실험 방식에 대해 Compute goodness for every label은 위의 MNIST 실험에서 살펴본 것이며, one-pass softmax는 최종 Output layer에서의 goodness를 사용한 것으로 보입니다.

이번 논문은 사실 한 주에 걸쳐 쓰기에는 쉽지 않았던 것 같습니다. 무엇보다 딥러닝 전반적인 지식을 가지고 있는 채로 작성해야만 수월하게 설명하고 다양한 관점에서 이야기를 풀어나갈 수 있었을 것 같은데, 그러지 못한 상태에서 읽다보니 초반부에 많이 어려웠던 것 같습니다. 추후 연구가 더욱 진행된다면, 해당 논문이 센세이션을 불러올 수 있지 않을까하며 지금은 방법론에 대해 간단히 이해하고 넘어가려고 합니다. 이상으로 리뷰 마치겠습니다.