오랜만에 Active Learning 에 대한 분석을 제시한 논문을 가져왔습니다. 해당 논문은 Active Learning에서 Initial pool에 따른 성능 차이가 있음에 주목하며, 이 초기 레이블 풀이 성능을 향상시킬 수 있는지를 분석한 논문입니다. 참고로 해당 논문은 NeurIPS 2020 Workshop 이자, Machine Learning Research 2021 저널에 동시에 게재된 논문입니다.
On Initial Pools for Deep Active Learning

- Paper: NeurIPS 2020 Workshop on Pre-registration in Machine Learning, [ 바로가기 ]
- Author Video: YouTube
- Code: GitHub
Background
아마 그동안 저의 세미나를 열심히 들으셨던 연구원분들이라면, Active Learning하면 ‘랜덤성 이슈’가 있다는 것을 잘 알고 계실 겁니다. Active Learning 방법론에 대한 세미나를 진행하면, 제법 많은 연구원분들께서 “발표하신 논문은 랜덤성에 대한 고려를 하지는 않았나요?” 라는 질문을 하기도 하죠. 여기서 랜덤성이라 함은, 많은 AL 연구에서 다양한 변수가 있음에도 불구하고, 변수가 고정되지 않은 채 논문 및 연구가 진행되고 있음을 의미합니다.
따라서 최근에는 이런 AL 연구에 대한 한계를 지목하며, AL의 한계 및 분석을 제시한 논문이 등장하고 있습니다. 이에 대한 저의 리뷰도 있으니 궁금하신 분들은 아래 리스트를 확인하시기 바랍니다.
- [ICCV Workshop 2021] Reducing Label Effort: Self-Supervised meets Active Learning
- [WACV 2023] Randomness is the Root of All Evil: More Reliable Evaluation of Deep Active Learning
- [CVPR 2022] Towards Robust and Reproducible Active Learning using Neural Networks
제가 오늘 리뷰하려는 논문은 초기 레이블 셋에 대한 고찰을 담은 논문입니다. Active Learning 의 여러 변수 중 하나가 이 초기 레이블 셋 이라고 해도 과언이 아닙니다. 그렇다면 이 초기 레이블 셋이란 무엇일까요? 이를 이해하기 위해서는 Active Learning이 무엇인지부터 알아야합니다. (Active Learning 에 대해 어느정도 지식이 있으신 분들은 지금부터 설명하는 부분을 뛰어넘고 바로 본론을 읽으시는 걸 추천드립니다.)
한 줄로 요약한다면 제 생각에 Active Leanring (이하 AL)이란 성능을 높일 수 있는 하위 데이터 집합을 선택하는 연구입니다. 사실 AL은 라벨링 비용을 어떻게 하면 줄일 수 있을까? 라는 의문에서부터 시작된 연구라고 볼 수 있는데요. 예를 들어 설명을 드려보겠습니다. 만약 훈이가 라벨링에 소비할 수 있는 예산은 B원이라고 해봅시다. 그 때 라벨링 비용이 장당 k원이라고 한다면, 저는 (k * n <= B)를 만족시키는 n장만큼 라벨링을 할 수 있겠네요. 그렇다면 훈이는 똑같은 n장의 데이터에 대해 라벨링 하더라도, 라벨러(혹은 어노테이터/오라클, 라벨링을 하는 사람을 의미)가 더 어렵거나 복잡한 데이터에 대해 라벨링해주기를 희망할 것입니다. 같은 가격이라 할지라도 기왕이면 뽕을 빼고 싶은 인간의 심리라고나 할까요ㅋㅋ
위 예시에서의 훈이가 ‘어렵거나 복잡한’ 데이터를 라벨링하기를 희망한 것처럼, Active Learning 에서는 성능을 더 높일 수 있는 데이터를 찾고자 합니다. 즉, 동일한 size의 Label dataset으로 모델을 학습할지라도, 모델의 성능을 더 높일 수 있는 데이터셋을 찾고싶은 것이죠. 저는 이것을 ‘데이터의 가치’로 정의하겠습니다. 가치 있는 데이터라고 한다면, 모델의 성능을 더 높일 수 잇는 데이터셋이죠. 따라서 Active Learning 에서는 데이터의 가치를 판단하는 모델을 학습하는 방법에 대해 연구하고 있습니다. 똑같은 크기의 데이터셋을 사용해서 학습하더라도, 모델의 성능이 더 좋은 데이터셋을 찾는 연구라니 제법 멋지지 않나요 ㅎㅎ?
자 이제 Active Learning 이 무슨 연구인지는 충분히 이해하셨을 것이라 생각이 듭니다. 그럼 이 Active Learning에서 모델 학습은 어떻게 하고, 평가는 어떻게 하는 지에 대해 알아봅시다. Active Learning에서 모델을 학습하는 구조는 ‘주기’를 가지고 학습된다는 특징을 가집니다. ‘주기’의 사전적 정의는 ‘같은 현상이나 특징이 한 번 나타나고부터 다음번 되풀이되기까지의 기간’ 인데요. Active Learning 은 특정 프레임워크가 일정 횟수만큼 반복된다는 특징을 가집니다. 이해를 돕기 위해 그림과 함께 설명드리겠습니다, 아래가 바로 Active Learning 의 구조에 대한 그림입니다. (해당 그림은 “A Survey of Deep Active Learning” 논문에서 가져왔습니다)
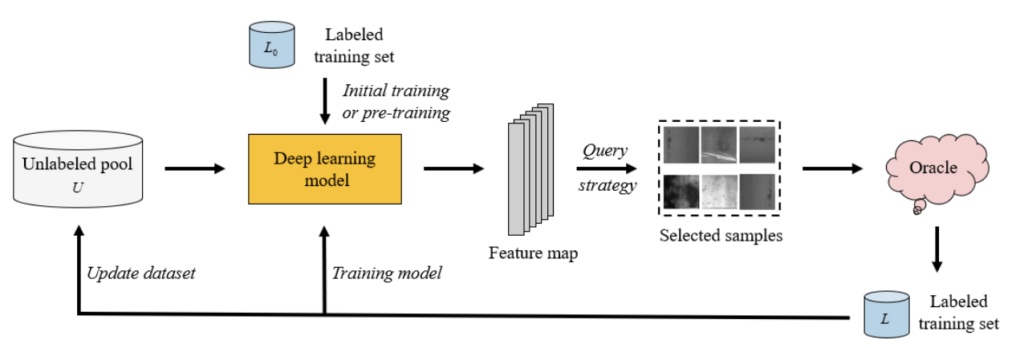
[0. Sampling the Initial Labeled set] 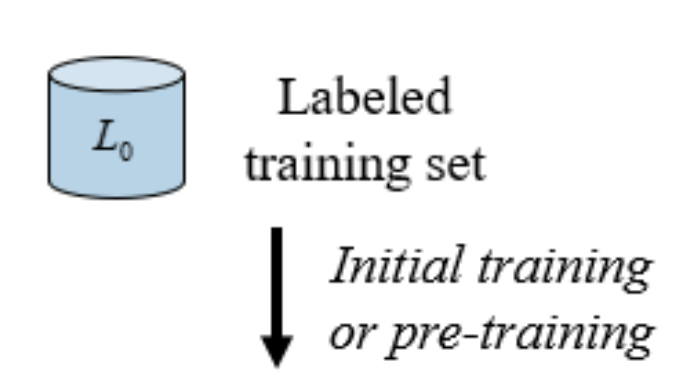
Active Learning에서의 모든 학습은 지도학습으로 진행됩니다. 그러므로 가치판단 모델을 학습하기 위해서는, 필연적으로 레이블이 있는 데이터셋이 필요하죠. AL에서는 보통 전체 데이터셋의 1%~10% 정도의 소량의 데이터셋에 레이블이 있다고 가정합니다. 이렇게 초기 가치 판단 모델 학습을 위해 존재하는 초기 레이블 데이터셋을 Initial label pool 혹은 inital label dataset 이라고 부릅니다. 일반적인 AL에서는 전체 데이터셋에서 랜덤하게 Initial label pool 을 선택합니다. (기존에는 이 초기 레이블 셋을 어떻게 선별할 지에 대해서는 집중하지 않고, 그저 여러 개의 랜덤 시드를 사용하여 초기 레이블 셋을 선별하였습니다.)
[1. Train]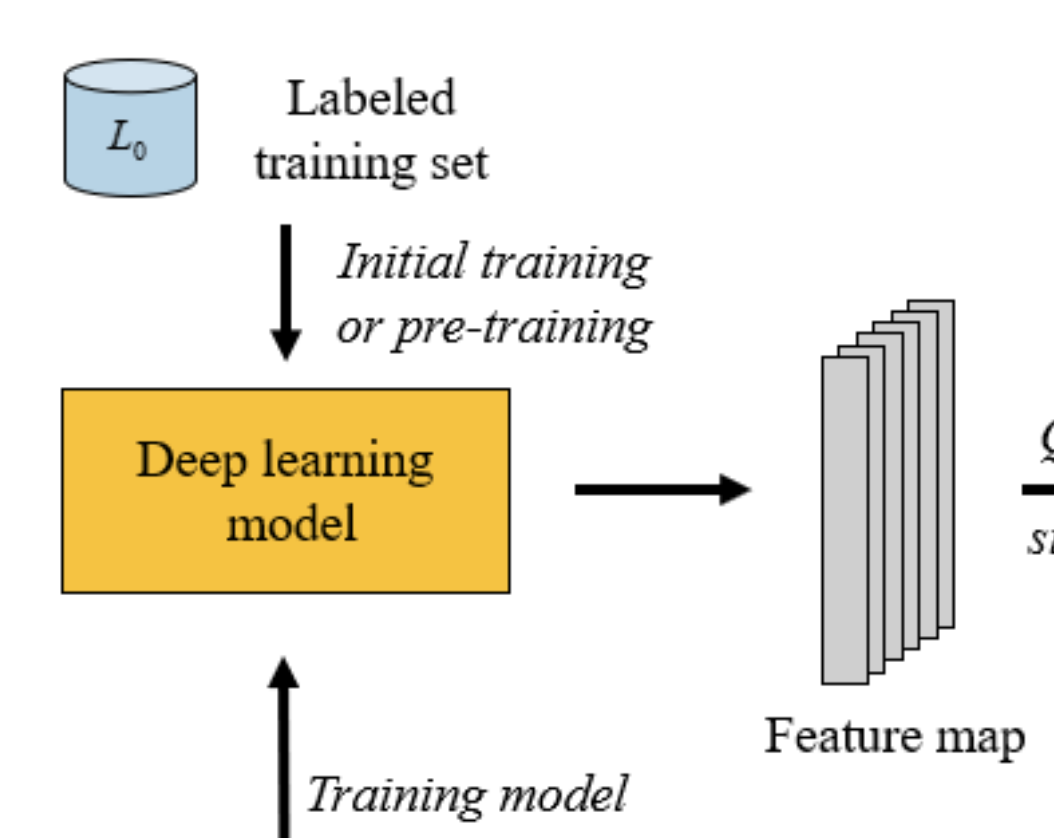
0단계에서 초기 레이블 데이터셋에 대한 준비가 완료되었다면, 이제부터는 그 Initial label dataset을 사용하여 가치 판단 모델을 학습합니다. 모델은 데이터의 가치를 잘 표현해 feature를 출력하도록 학습이 되겠지요. 많은 논문에서는 초기 레이블 데이터셋이라고 하여 L_0라고 표기합니다.
[2. Selection]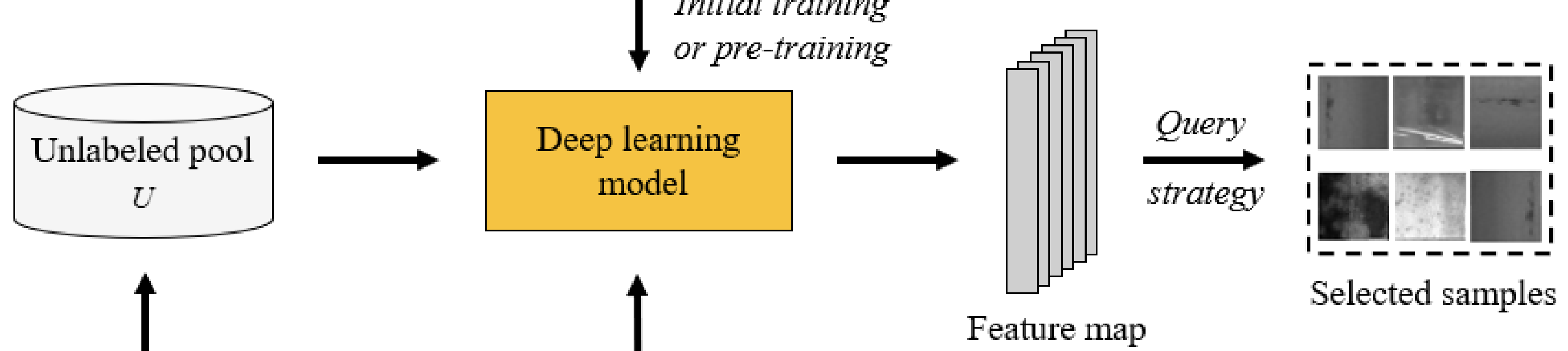
initial label dataset을 사용하여 데이터의 가치를 판단하는 모델이 학습 완료되었다면, 이제 레이블링이 필요한 데이터셋을 선별하는 단계입니다. 레이블이 없는 Unlabeled dataset을 이제 학습이 완료된 모델에 태웁니다. 그럼 모든 Unlabel data들은 feature 가 출력되겠지요. 그럼 이제 가치 있는 데이터를 선택하기 위해 저자가 제안하는 selection metric(sampling strategy/method) 에 따라 데이터의 가치를 판단합니다. selection metric은 말 그대로 데이터를 선택할 방법으로, 어떤 데이터가 가치있는 데이터인지를 결정하는 기준이 됩니다. 예를 들어 결정 경계 근처에 있는 데이터들은 모델이 어떤 클래스인지 판단하기 어려운 불확실할테고, 이런 데이터에 대한 모델의 오답률이 높을테니 이 결정 경계 근처의 데이터에 대해 우선적으로 라벨링하도록 선택하도록 selection metric을 설계할 수 있습니다. 이 기준에 따라 모델은 Budget(미리 정의한 labeling할 데이터의 개수) B개를 선별하게 됩니다.
[3. Labeling]
이제 B개의 데이터를 선별했다면, 그 데이터셋들에 대해 레이블을 추가하도록 오라클(라벨러, 어노테이터)에게 요청(Query)하는 단계입니다. 실제 상황이라면 뭔가 Active Learning 에서는 터미널에서 라벨링하는 과정이 포함되어 있나..? 라는 생각이 들기도 할 텐데요, 실제로는 아닙니다. AL에서는 보통 CIFAR-10, CIFAR-100에 대한 데이터셋을 사용하여 실험을 진행하는데 아시다시피 해당 데이터셋들은 이미 레이블이 존재합니다. 따라서 이 단계에서 AL 구현에서는 기존에 존재하는 레이블을 불러옵니다.
[4. Addition & Re-Train]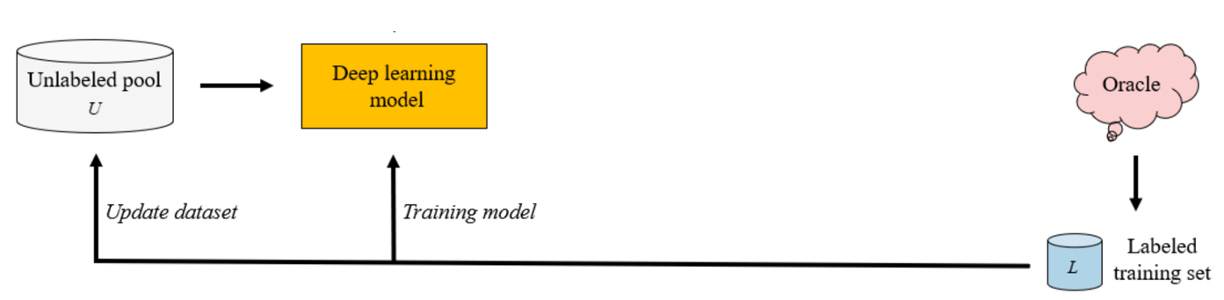
오라클로부터 B개의 데이터에 대하여 레이블을 얻었습니다. 1번째 요청에서 얻은 레이블 데이터쌍이라고 하여 보통 L_1 이라고 표기합니다. 이렇게 얻은 L_1은 Unlabeled pool에서는 제거하고, 그와 동시에 기존에 존재하던 Labeled pool인 L_0에 추가합니다. 그렇게 L_0 + L_1의 labeled set을 얻게 되었습니다. 그럼 다시 그 labeled set을 사용하여 모델을 재학습합니다.
[5. [2]~[4] Cycle]
이제 정해진 횟수만큼 [2]단계부터 [4]단계까지 과정을 반복합니다. 정해진 횟수는 논문마다 다릅니다. 선별하는 데이터의 개수 B 역시 논문마다 다릅니다. 그리고 Active Learning 에서 성능 평가는 보통 가치 판단 모델의 학습이 완료되었을 때 진행합니다. M번의 주기 학습을 반복한다면, 성능 평가 역시 M번을 진행하게 되죠. AL에서는 보통 데이터를 계속 추가하면서 성능을 평가할 때, 같은 데이터의 개수를 가지고 더 높은 성능을 낼 경우 혹은 동일한 성능을 달성하되 사용한 데이터 개수가 더 적을 경우 더 뛰어난 방법론이다 라고 평가합니다.
지금까지 Active Learning이 무엇인지, 그리고 어떤 프레임워크를 지녔는지, 실험 결과를 해석하는 방법에 대해 알아보았습니다. AL의 디테일한 부분까지 설명드린 것은 아니지만, 이정도만으로 해당 논문의 리뷰를 이해하는 데에는 어려움이 없을 거라 생각됩니다. 지금부터 본격적인 리뷰를 시작해보겠습니다.
Introduction
Background를 통해 알아본 Active Learning 연구는 지금까지도 활발하게 진행되고 있습니다. 그런데 그동안은 연구들은 대부분 모델 설계(어떻게 feature를 생성할지) 혹은 selection metric(가치 있는 데이터 선별 기준)에 대해 초점을 뒀습니다. 특히 initial label pool에 대해서는 특별히 고려하지 않고, 그저 랜덤하게 선택해서 학습을 시작하는 경우가 대부분이었습니다.
본 논문에서는 단순 Random sampling이 아닌 다른 방법으로 샘플링된 initial labeled pool을 사용했을 때의 영향과 결과를 분석하였습니다. 특히 활발하게 연구되어기도 있는 self-supervised learning과 클러스터링 방법을 사용하여 초기 레이블 풀을 결정하는 기법을 제안하였습니다.
Methods and Experimental Protocol
1) Proposed Initial Pool Sampling Strategies
초기 레이블 셋을 선택하는 기법으로 저자는 unsupervised/self-supervised 에 주목하였습니다. 해당 태스크는 모두 레이블이 없지 학습할 수 있다는 특징을 가집니다. 그리고 이 기법으로 학습된 모델이 어려워하는 데이터셋으로 초기 레이블 셋을 선택하는 것이, AL 모델 학습에 도움이 될 것이라는 가설에 기반하여 초기 레이블 데이터셋을 선택하고자 하였습니다. (실제로 [ICCV workshop] 이 논문에서도 회전각을 예측하는 self-supervised learning 이 어려워하는 데이터를 AL 모델 역시 어려워함을 실험적으로 보이기도 했습니다.)
사실 레이블이 전혀 없는 상태에서 AL 모델에 좋은 데이터셋을 선택하기 위해서는… 비지도학습/자기지도학습 기법을 사용하여 초기 라벨링 셋을 선택하는 것이 당연한거 아니야? 라고 생각하실 수 있을 것 같은데요… 그런 방법을 사용한 연구들이 최근에서야 등장하였고, 초기 레이블 셋 선택에 대해 집중한 연구가 당시에 흔치 않았기에, unsupervised/self-supervised 기법을 사용한 것이 제법 인상 깊은 차별점이 될 수 있을 것 같습니다. 그럼 저자가 unsupervised/self-supervised를 어떻게 사용하였는지에 대해 설명드리도록 하겠습니다.
Self-Supervision Methods
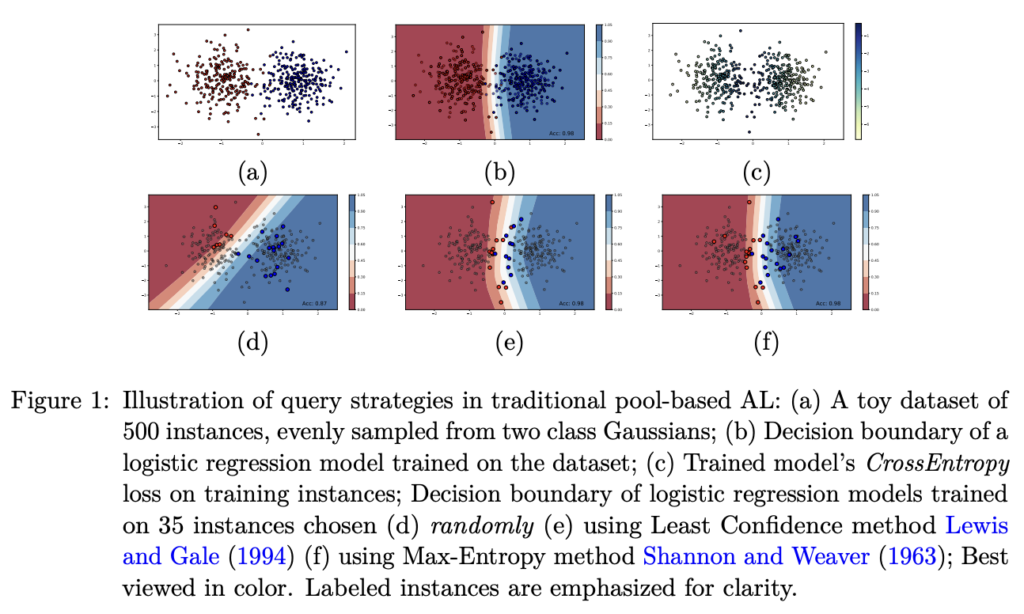
우선 위의 그림을 통해 초기 레이블 데이터셋을 선택하는 방법이 왜 중요한지를 설명드리겠습니다. (a) 는 가우시안 분포에 따른 500개의 데이터샘플을 2개의 클래스로 랜덤하게 설정한 것입니다. (b)는 전체 데이터셋으로 학습된 로지스틱 회귀 모델 결정 경계입니다. (c)는 앞서 학습한 모델에 대한 cross-entropy loss를 색으로 표기한 것입니다. 아래 행 그림들은 전체 데이터셋중에서 35개의 데이터를 선택하는 방법에 따른 결정 경계인데요. (d)는 랜덤하게 (e)는 Least confidence를 그리고 (f)는 Max-Entropy 입니다. (참고로 e, f는 AL에서 사용하는 대표적인 selection metric입니다) 여기서 주목할 건, (d)는 실제 전체 데이터 분포에 대한 결정 경계와 전혀 다른 경향을 보이고 있습니다. AL에서 데이터 가치 판단 모델은 초기 레이블 데이터셋을 사용하여 데이터 가치를 결정하는데, 처음 선택된 데이터부터 전혀 다른 경향을 보인다면.. 모델은 전혀 다른 방향으로 학습될 수 있습니다. 특히, Semi-supevised나 Active Learning 같이 소량의 레이블 데이터셋으로 시작하는 학습 기법의 경우 어떤 데이터를 처음 학습으로 사용하느냐는 아주 중요한 문제입니다.
초기 레이블 데이터셋으로 어떤 걸 선별하는 것이 중요한 문제인지는 알겠습니다. 또한 (e) (f)에서 사용하는 AL의 대표적인 데이터 선별 방법 역시 충분히 설득력 있는 기법인 것도 알겠네요. 그렇다면 초기 레이블 데이터셋을 선별할 때도 (e), (f)에서 사용하는 기법을 적용하면 되지 않을까요? 정답은 그럴 수 없다 입니다. (e), (f)는 모델의 예측값과 정답값을 비교하여 불확실성을 판단하는데… 초기 레이블 데이터를 선별할 때는 정답값이 없습니다. 그렇기 때문에, 저자는 레이블이 없이도 모델을 학습할 수 있는 Self-supervised Learning 에 주목하였습니다. 그리고 self-supervised learning 과정 중 모델이 오답을 낸 데이터일 경우, Active Learning 에서도 마찬가지로 어렵다고 판단할 것이라고 가정하였습니다. 즉, Self-SL 모델이 어려워한 샘플은 라벨링이 필요할 어려운 샘플이니까, 이 데이터셋을 초기 레이블 셋으로 정답을 알고 시작하자는 생각이죠.

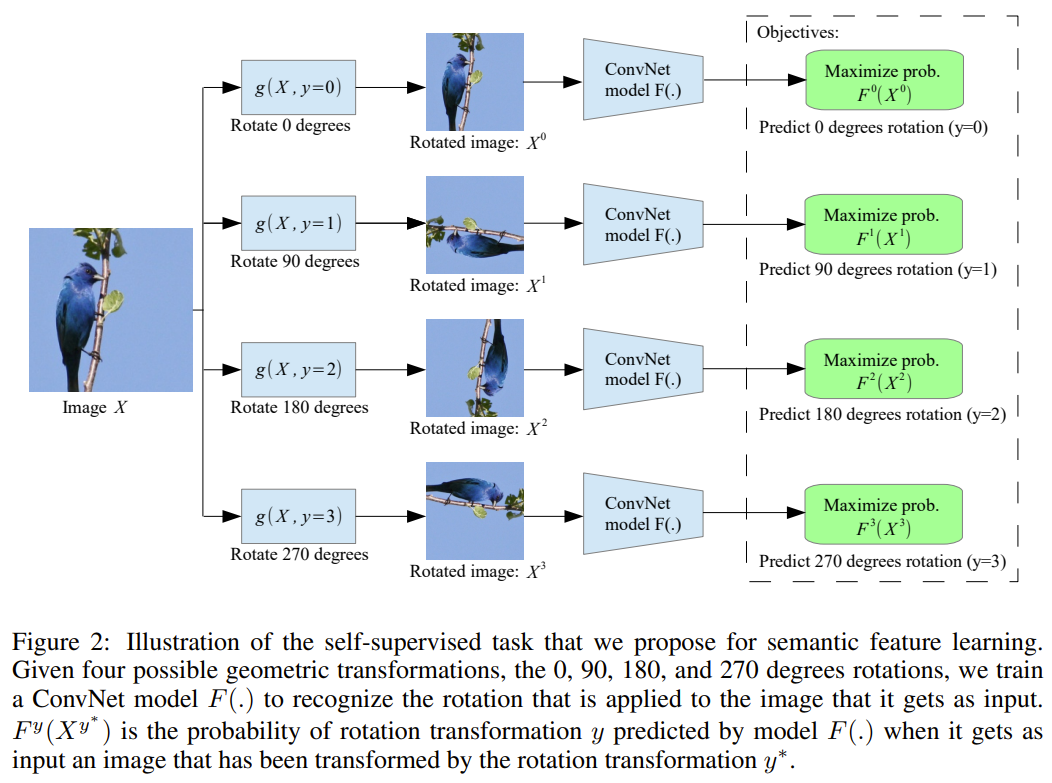
따라서 Self-SL 기법으로 저자는 image inpainting, image rotation prediction을 사용하였습니다. 위의 그림 중 왼쪽이 image inpainting, 오른쪽이 image rotation prediction에 해당합니다. 뿐만 아니라 VAE 도 이를 위해 사용하였다고 합니다.
Unsupervised Learning (Clustering) Methods
데이터를 선별하는 기준으로 불확실성을 택할 경우, 레이블링된 데이터가 점차 편향될 수 있다고 합니다. 즉, 전체 데이터셋의 분포는 D라고 할 때, AL 주기 학습이 반복되며 labeled set은 점차 분포 D와 비슷해져야 하는데, 초기 레이블셋 분포인 D’에서 벗어나지 못하기도 한다는 것이죠. 따라서 Uncertainty와 반대되는 진영에서는 데이터를 선별하는 기준으로 Uncertainty가 아닌 Diversity를 선택하였습니다. Diversity 기반의 AL 연구진의 목표는 초기 레이블 셋이 D’ 라고 하더라도, 점차 주기 학습이 반복되며 최종적으로 분포 D가 되도록 전체 데이터셋을 대표하도록 하는 것이죠. 이 연구진들은 데이터를 선별할 때, k-means와 같은 비지도 학습 기반의 방법론을 사용합니다. 따라서 저자도 그럼 이걸 초기 데이터를 선별하는 기준으로 선정해보았다고 합니다.
이를 위해 저자는 DeepCluster와 k-means를 사용하여 클러스터를 초기 레이블 데이터로 사용하였습니다.
Experimental Results
저자는 실험을 위해 MNIST, CIFAR-10, CIFAR-100, Tiny-ImageNet을 사용하였습니다.
Modifications to the Original Proposal
몇 가지 변경 사항이 있는데 중요한 것만 짚고 넘어가겠습니다. (아마 워크샵 이후 추가 실험 결과를 반영하기 위해 작성한 파트 같습니다)
Switching to Better Performing Tasks: 처음에는 이미지 회전 예측과 이미지 인페인팅을 Self-SL로 사용하였다가, SimCLR로 변경하였다고 합니다. (아마 훨씬 성능이 좋은 SimCLR를 적용한 추가 실험을 Workshop 이후 진행 한 뒤, 실험 내용을 변경한 것 같습니다). 또한 비지도 학습의 경우 DeepCluster를 SCAN으로 전환하고, 이때 pretext task로서 SimCLR를 사용하였다고 하네요. 왠지 실험에는 분명 SimCLR와 SCAN이 있었는데, 위에 설명에는 왜 없나 했네요.. SimCLR에 대한 리뷰는 워낙 많으니 저는 여기서의 설명은 생략하도록 하겠습니다.
Initial Pool Sampling Details
이제 어떻게 초기 레이블 셋을 선별하였는 지에 대한 설명입니다. 사실 어떤 샘플을 선택하였는지는 간단합니다. Loss가 높은 데이터셋을 선별하였다고 설명하면 명쾌하지 않을까 싶네요.
- SimCLR: 학습이 완료된 모델에 대해 unlabeled sample에 대해 4가지 augmentation 이미지 간 평균 대비 Loss 점수를 할당한 뒤, 높은 데이터셋을 선별하였습니다.
- VAE: 수렴할때까지 전체데이터셋에 대한 VAE모델을 학습합니다. 그 다음 reconstruction error가 높은 데이터를 선별합니다. VAE를 선별한 이유로는 SimCLR보다 VAE가 간단했기 때문이라고 합니다. 즉 task의 복잡성이 초기 풀 효율성에 어떻게 기여하는지를 확인하기 위해 선별하였다고 밝혔습니다.
- SCAN and K-Means: SCAN은 self-SL task를 기반으로 학습한 피처를 기반으로 구축됩니다. 따라서 학습이 끝나면 SCAN모델은 각 데이터에 대한 클러스터를 할당합니다. K-Means의 경우, SimCLR로 학습한 피처에서 K-Means 알고리즘을 적용하여 클러스터를 할당합니다. 이 클러스터들이 초기 샘플이 되겠지요. VAE를 선택한 이유와 마찬가지로 모델의 복잡성에 따른 성능을 판단하고자 매우 간단한 K-Means와 보다 정교한 SCAN을 선택했다고 밝혔습니다.
Main Experiments
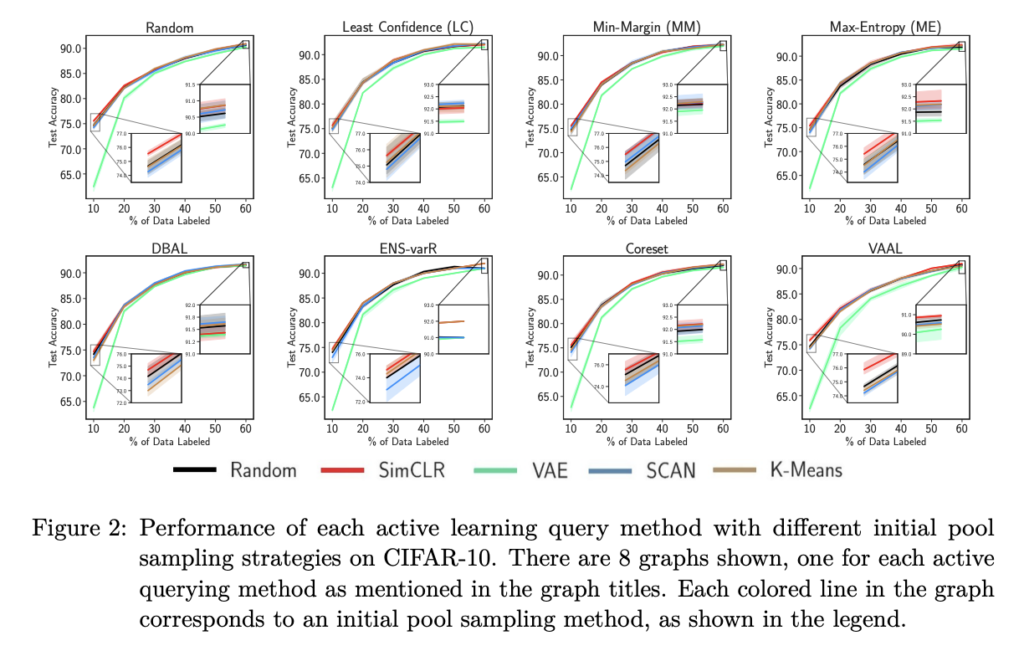
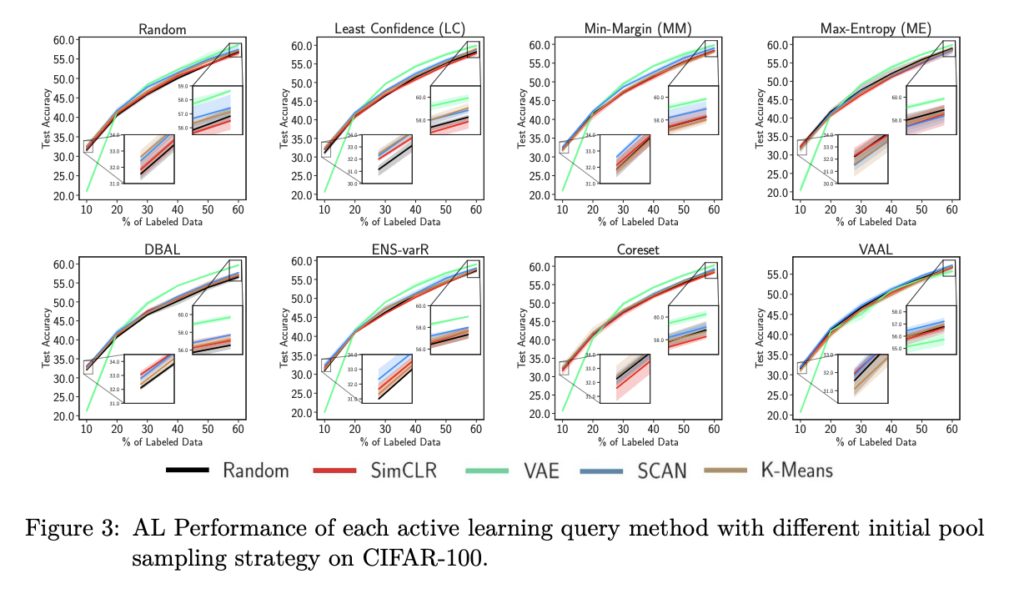
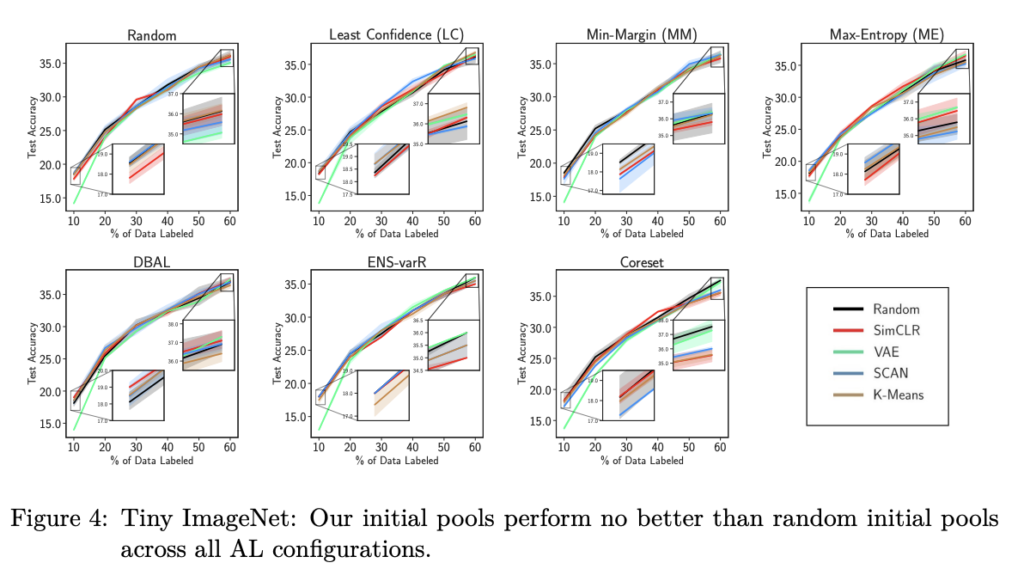
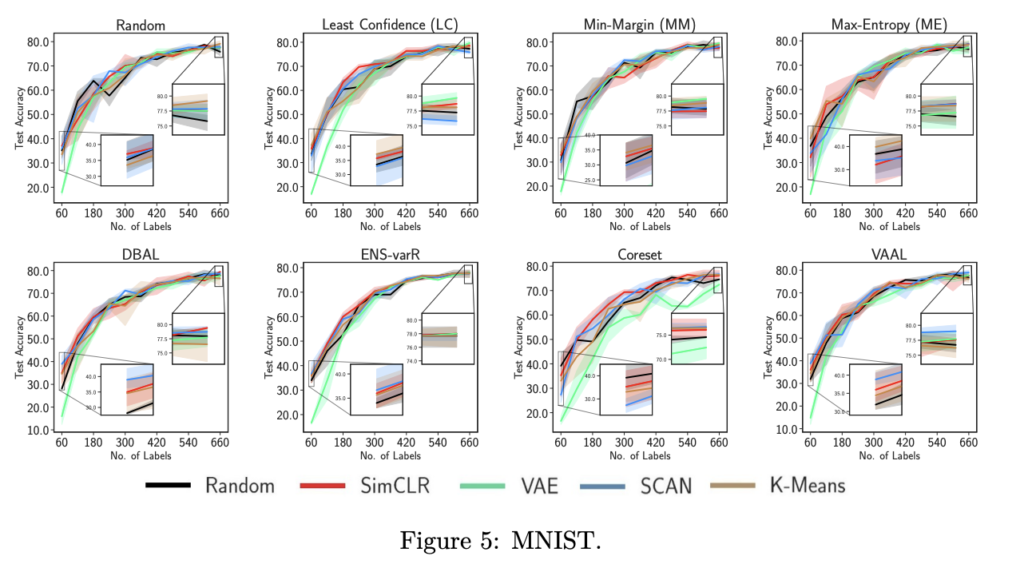
지금부터는 적합한 초기 풀을 찾기위한 실험들을 나타냅니다. 아래 그림 4개(그림 2부터 5)는 차례대로 CIFAR-10, CIFAR-100, Tiny-ImageNet, 그리고 MNIST입니다. 각 실험 테이블 위에 적혀있는 것이 샘플링 기법(Random, Least Confidence, ..etc) 입니다. 각 테이블에서의 여러 라인들이 초기 레이블을 선별하는 방식입니다.
이제부터 각 초기 풀 샘플링 전략에 대한 결과를 분석해보도록 하겠습니다.
- SimCLR
- 그림 2(CIFAR-10) 중 8가지 세팅에서 Random initial pool로 학습한 모델이 SImCLR로 샘플링된 것보다 더 나은 성능을 보였습니다. 그러나 시작은 좋았으나, 주기가 계속되면서도 계속 좋은 샘플을 선택하지는 못했습니다. 그 결과 마지막에는 random과 유사한 성능을 보였습니다.
- 그림 3(CIFAR-100)에서도 Random과 비슷하거나 오히려 떨어지는 걸 볼 수 있었습니다. 이는 Tiny-ImageNet, 그리고 MNIST에서도 비슷한 경향을 보였습니다.
- SCAN and K-Means
- SCAN과 K-Means는 랜덤 초기 풀보다는 더 나은 모델 성능에 기여하는 것으로 보였습니다.
- VAE
- 놀랍게도 VAE는 4개 데이터셋 모두에서 일관되게 처음 주기에서 성능이 저조했습니다.
- CIFAR-10의 경우, 첫 번째 주기에서 VAE 초기 풀로 학습된 모델과 다른 초기 풀로 훈련된 모델 간의 평균 테스트 정확도 차이는 12%였습니다. 마찬가지로 CIFAR-100의 경우 11%, Tiny Imagenet의 경우 4.5%, MNIST의 경우 18%의 차이가 있었습니다. 이는 초기 풀 샘플링과 AL에 사용된 모델의 차이 때문인 것으로 보인다고 합니다. 게다가 어느 한 모델(예: VGG16)에서 AL을 통해 선별된 데이터셋들은 다른 모델(예: ResNet-18)로 잘 전송되지 않는다는 것이 경험적으로 증명한 논문들도 있습니다.
- 저자는 이에 대해 일반적인 VAE 사용 추세에 따라 인코더와 디코더에 각각 4개의 컨볼루션 레이어가 있는 간단한 VAE 모델을 사용했기 때문에 이러한 큰 차이가 발생했을 수 있다고 주장하였습니다.
충격적이게도 저자는 모든 AL 주기가 끝날 때, CIFAR-10, Tiny Imagenet 및 MNIST에서 모든 초기 풀이 거의 유사한 정확도로 수렴하는 것을 볼 수 있으며, 이는 AL 성능에 큰 개선이 없음을 시사한다고 합니다. 결과를 요약하면, 저자가 제안하는 방법이 장기적으로 AL에 도움이 되는 좋은 초기 풀의 존재를 증명하지는 못했…다고 하였습니다.
사실 초기 레이블 셋에 따른 성능 차이에 대해서는 잘 알고 있던 부분인데요. 최근 ECCV 2022에 발표된 논문은 이 초기 레이블 셋 선택법으로 Self-supervised Leanring 을 사용하였다는 점에서 초기 샘플링 기법의 중요성 역시 잘 알고 있던 부분이기도 합니다. 그런데 역시 초기 레이블 샘플링 기법 및 분석을 제시한 연구가 이미 있었다니.. 그런데 결과가…. 생각보다 좋지 않네요… rotation, inpainint에 대해서도 다뤄주었으면 좋았을 걸 아쉬움이 있습니다. 리뷰 마치겠습니다.
안녕하세요 홍주영 연구원님 좋은 리뷰 감사합니다.
리뷰를 읽다가 궁금한 점이 있어 질문 드리겠습니다.
데이터를 선별하는 과정에 대한 질문인데요, uncertainty기반은 모델의 결정 경계 부분, 즉 모델이 명확히 구별할 수 없는 데이터를 우선적으로 선별하는 방식으로 이해하였습니다. 그렇다면 Diversity는 전체 데이터셋의 분포를 반영하여 데이터를 선별한다고 하셨는데 구체적으로 어떤 방식으로 선별이 이루어지는지 잘 모르겠습니다.
해당 논문이 Uncertainty나 Diversity 기반의 Active Learning 방법론을 제시한 건 아니어서 그 내용은 제가 굳이 다루지 않았는데요. 논문에서 비지도학습 기법으로 언급한 것 처럼 K-means와 같이 클러스터를 사용하여 레이블 셋과 가장 멀리 있는 샘플을 선택하여 전체 분포를 커버할 수 있는 데이터를 선별하는 것을 목표로 합니다.
안녕하세요 좋은리뷰 감사합니다
많은 AL 논문에서 random 선별 방식이 꽤 높은 성능을 보이는 경우가 있습니다.
그러나 Figure1에서는 random으로 선별한 결과가 비교적 좋지 않은데
혹시 cold start와 같은 변수때문이 아닌지 궁금합니다
Figure1은 초기 라벨 셋의 중요도를 보여주기 위한 실험으로 아마 Cold-start 의 일종일 수 있겟으나, 완전히 맞다고 하기엔 어려움이 있어보입니다. 사실 해당 그림을 통해 저자가 보이고자 한 내용은 초기 레이블 셋을 고려해야하는 이유를 보여주기 위한 실험이기 때문이죠
안녕하세요 홍주영 연구원님, 좋은 리뷰 감사합니다. background까지 친절히 설명되어 있어서 논문을 읽는데 큰 도움이 되었습니다.
리뷰를 읽고 제가 이해한 바로는 다음과 같습니다.
1. labeling은 cost가 높은 task이기 때문에, 우리는 고가치 데이터(학습 효율이 좋은 데이터)를 선별하고 싶습니다. 이와 관련된 연구 분야가 active learning입니다.
2. active learning은 지도학습으로 진행되기 때문에, 가치판단 모델을 학습하기 위해서 레이블이 있는 초기 데이터셋이 필요합니다. 이 초기 레이블 데이터셋을 initial label pool이라고 합니다.
3. active learning 연구가 활발히 진행되고 있지만 기존에는 모델 설계와 selection matrix(데이터 선별 기준) 연구에 초점이 맞춰져 있었고, 초기 레이블 셋 선별 방법에 대해 집중하지 않았습니다. 초기 셋 선별에는 단순히 random seed를 이용하였습니다.
4. 본 논문에서는 random sampling이 아닌 다른 방법으로 initial labeled pool을 구성했을때의 영향을 다룹니다. self-supervised learning과 clustering을 사용해 initial label set을 구성하는 방법을 제안합니다.
5. 데이터 선별 기준으로 불확실성을 택할 경우 labeled data가 편향될 수 있으므로 uncertainty가 아닌 diversity를 기준으로 삼습니다. 이를 위해 DeepCluster와 K-means를 사용합니다.
6. SimCLR,VAE,SCAN,K-Means..? 의 방법을 사용하여 다양한 실험을 진행했지만, 결과적으로 논문 저자가 제안한 방법들이 AL에 도움이 되는 좋은 initial set을 보장하지 못합니다.
지금까지 성능 면에서 SOTA를 달성하거나, 적어도 새로운 방법론을 적용해서 유의미한 개선을 보여준 논문들만 봤었는데, 이렇게 결과가 좋지 못한 논문을 처음 봐서 신선했습니다. 또, 제가 아직 SimCLR, VAE, SCAN등과 같은 방법론을 잘 몰라서 글을 깊게 이해하지는 못했지만.. self-supervised learning, 그리고 active learning에서 초기 레이블 셋 구성이 굉장히 중요하다는 것을 알게 되었습니다.
리뷰를 읽다보니 궁금한 점이 생겨서 질문 남깁니다.
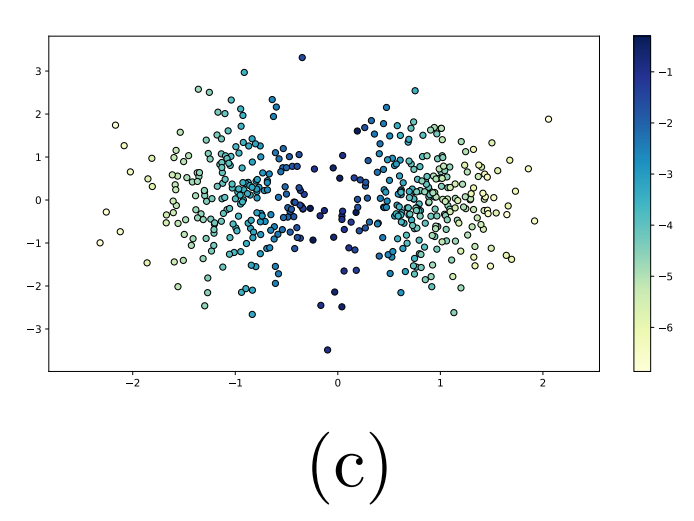
1. 중간에 첨부하신 Figure1에서 (c)의 색깔이 잘 보이지 않아서 어떤 경향성을 보이는지 잘 파악이 되지 않습니다. 혹시 어떻게 분포되어있는지 말씀해 주실 수 있을까요?
2. 그리고, least confidence는 가장 높은 confidence score가 낮은 데이터를 선별하는 것 같은데, uncertainty 방법으로 데이터를 선별하는것과 같은 것이라 생각해도 될까요?
3. 논문 내용과 관련있는 것은 아닌데, 뉴립스 워크숍은 뉴립스와 다른건가요?
답변 주신다면 감사하겠습니다.
안녕하세요 허재연 연구원님 질문 감사합니다.
우선 요약해주신 글을 읽으니 완벽하게 이해하신 듯 합니다. 🙂
우리가 익숙한 논문은 대개 SOTA를 달성하거나 특정 문제점을 해결한 “방법론”을 제시하는 논문일 겁니다.
그러나 이와 반대로 “분석”을 제시하는 논문도 많이 있습니다. 해당 연구는 후자에 해당하는 연구입니다. 그래서 결과가 안좋은 결과도 리포팅할 수 있는 듯 합니다.
(TMI를 하자면, 저는 이 논문을 읽고 제가 언젠가는 할 것 같은 실험 즉, 궁금했던 게 명쾌하게 해결되어서.. 해당 논문의 결과가 수치상으로 안좋을지라도 저에게는 좋은 논문입니다..ㅎㅎ)
이제 질문에 답변을 드리겠습니다.
이게 설명을 드리려고 했는데, 명확하게 설명이 안되어서 Figure 1 바로 아래 추가로 그림을 첨부하였습니다ㅋㅋ 확인부탁드립니다! 추가로 설명을 드리자면, 결정 경계 근처에 있는 샘플들은 cross entropy loss가 높습니다. 그리고 결정 경계에서 멀어질수록 loss가 작아지는 분포를 보이고 있습니다.
네, 허재연 연구원님이 말씀하신게 맞습니다. Least confidence는 가장 대표적인 Rule 기반의 Uncertainty 입니다.
네, 둘은 완전히 다릅니다. 뭔가 이론적으로 설명드리자면, 워크샵은 학회와 동시에 진행하나 조금 더 작은 세부 주제 몇 가지가 정해져 있습니다. 그래서 워크샵에서는 비슷한 연구를 하는 더 작은 그룹의 연구자들끼리 모여서 의견을 나눌 수 있습니다. (그러나 학회에 게재되는 논문이 더 높은 평가를 받긴 합니다.)