안녕하세요. 일곱 번째 X-review 입니다. 이번 주 내 DETR과 Deformable DETR에 대해 다룰 예정으로, 해당 논문을 읽게된 계기는 한전 과제와 연관되며, Small object detection 성능을 높이고자 현재 CVPR 2023 에 제출한 하나의 논문을 참고하고자 했으며, 해당 방법론이 Deformable DETR을 토대로 하고 있기 때문에 DETR의 지식을 베이스로 쌓고자 읽게 되었습니다. 예전 김태주 연구원님께서 DINO라는 논문을 연구실 세미나에서 발표해주셨던 것으로 기억하는데, 기억나신다면 리뷰 사진 중 익숙한 사진이 하나 보이실 것 같습니다. 그럼 시작하겠습니다.

---

Abstract , Introduction, Related work, The DETR model

논문 제목에서 이미 익숙함을 느꼈을테지만, DETR은 NLP의 Transformer를 detection에 접목한 논문입니다.

저의 최근 리뷰 동향을 살펴보면 대부분 Transformer와 ViT에 대해서 다루고 있는데, 사실 DETR은 ViT 논문이 나오기 5달전 쯤 발표된 논문으로, ViT의 “입력 이미지를 패치 단위로 나누어 어텐션 연산을 한다”와 달리 CNN Backbone을 통과한 Feature map에 대해 Transformer의 연산을 진행합니다. 그렇단 말은 Pixel by pixel, 즉 Feature map의 모든 pixel에 대해 Self-attention을 진행하는 것이겠죠. 그렇다면 DETR에서 어떤 점을 해결하고자 했으며 자신들의 Main contribution은 어떤 것이라고 주장할까요?

• object detection을 direct set prediction의 문제로 접근

• Transformer의 encoder-decoder 구조를 통해 이미지 내 global한 정보를 학습

아마 두 번째의 Transformer의 Encoder-Decoder 구조에 대해서는 익히들 알고 있으실텐데, 아래 모델의 구조와 함께 다시 살펴보겠습니다. 그보다 첫 번째 contribution인 direct set prediction의 문제로 접근했다는 말이 어떤 의미인지, 자세히 살펴보겠습니다.

---

direct set prediction problem

논문의 핵심이라고 볼 수 있습니다. 먼저 단어 그대로, Set(집합)의 성질을 상기시켜 봅시다. 집합은 중복을 허용하지 않으며, 일정한 순서가 없다는 성질을 가지고 있습니다. 해당 성질을 토대로, 조금 있다 설명할 object query (집합)은 predict bounding box의 offset과 category label을 가지고 있습니다. 해당 object query들에는 중복이 없다는 점이 중요한데, 그렇다면 하나의 object query는 다른 object query와 겹치지 않는다, 다른 말로는 query 내 bounding box의 offset이 겹치지 않는다는 것을 의미하죠.

bounding box가 겹치지 않는다는 말로 하나 눈치챌 수 있을 것인데, 바로 NMS(Non-Maximum Suppression)이 필요하지 않습니다. 중요한 부분입니다. NMS가 필요하지 않을 뿐만 아니라 Pixel 간 어텐션 연산을 통해 영상 내 object가 있을 법한 위치의 offset을 알아내는 작업으로, 우리는 Anchor box를 설정하거나 혹은 RPN(Region-Proposal Network)과 같은 bounding box 후보들을 만들 필요가 없어졌습니다.

위의 문단이 논문의 핵심 내용이자 중요한 부분이니 다시 한번 상기하고 넘어가겠습니다. 우리는 object detection을 direct set prediction problem으로 접근하여, object query라는 set에 대한 end-to-end 예측으로 NMS, RPN, Anchor generator과 같은 human prior knowledge, hand-crafted engineering, postprocessing이 필요하지 않습니다. 이와 같은 중복을 피하는 문제는 object query라는 prediction과 ground truth 사이의 Bipartite matching, 이분 매칭을 통해 가능합니다.. Bipartite matching에 대해서는 아래에서 다시 살펴보며, 집합의 두 번째 성질인 순서가 없다라는 측면에서 살펴보겠습니다.

집합의 두 번째 성질인 순서가 없다면 이분 매칭의 결과에 따라 loss function이 공변하면 안됩니다. 불변해야하죠. 이는 한번에 와닿지 않을 것 같네요. prediction A와 ground truth B 간의 매칭이 있었다 가정하고, 이번에는 순서가 일정하지 않으니 prediction A가 ground truth C와 매칭이 있었다고 가정하면 둘 사이의 loss는 분명 다를 것 입니다. 순서가 없으니 prediction과 ground truth 사이 일대일 매칭 결과에 따라 일정한 loss를 내뱉는다는 확신이 없는데, 이를 가능하게 한 것이 Hungarian 알고리즘입니다. 자 그럼, Hungarian 알고리즘을 알아보면서 loss function까지 한번에 살펴보겠습니다.

---

Hungarian algorithm

Hungarian algorithm이 어떤 역할을 하는지 다시 살펴보고 시작하겠습니다. Hungarian algorithm은 prediction set과 ground truth 사이 일대일 매칭, 즉 이분 매칭 (Bipartite matching)을 만듭니다. Hungarian algorithm이 풀고자 하는 문제는 “Complete bipartite graph에서, maximum-weight matching”을 찾는 일입니다. 이 때 Complete bipartite graph란 같은 집단 (subset) 안의 정점 (vertex) 끼리의 연결이 없으며, 다른 집단의 정점 간에는 가능한 모든 연결이 있는 그래프를 말합니다.

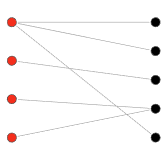
즉, 아래 그래프의 빨간색과 검은색 집합 내의 연결은 없으며, 서로의 집단 간에는 모든 연결이 가능한 그래프를 의미하죠. 그렇다면 maximum-weight matching이란? 연결 (edge)의 weight가 존재하는 그래프에서, 연결 시 모든 weight의 합산이 큰 연결 방식 (matching)을 찾는 일을 말합니다. 동일한 방식으로는 minimum-weight matching이 있습니다. 이러한 matching strategy는 결국 하나의 할당 문제 (Assignment problem)으로 볼 수 있습니다. 이 내용을 그대로 들고온다면, prediction set과 ground truth 간의 일대일 매칭에서 maximum-weight (확률 측면에서) 혹은 minimum-weight (loss 측면에서)를 찾는 일과 같겠습니다.

위의 정의만으로는 이해가 쉽지 않을 수 있습니다. 아래의 예시를 살펴봐야겠습니다. 다음의 예시는, mimum-weight matching을 위한 Hungarian algorithm으로, 회사 A, B, C의 cost 1, cost 2, cost 3의 일에 대해 각각의 비용을 지불해야할 때, cost 별로 하나씩만 선택할 수 있다면 어떤 조합이 최선일지를 찾는 과정입니다. 가장 쉽게는, Brute Force 알고리즘으로 가능한 모든 조합의 비용을 계산한 다음, 최소 비용에 해당하는 조합을 찾을 수도 있지만, 이는 O(n!)에 해당하는 수준의 비효율적인 연산입니다. 따라서 우리는 Hungarian algorithm을 선택하겠습니다.

	Cost 1	Cost 2	Cost 3
Company A	108	125	150
Company B	150	135	175
Company C	122	148	250

Step은 1 – 6 까지 있으며, 사실 이 모든 과정을 이번 기회에 설명하긴 하겠지만, 무엇보다 우리가 알아야할 점은 Hungarian algorithm으로 Bipartite matching 간 최적을 찾을 수 있다는 점입니다. 그래도 한번 아래의 아이디어를 토대로 살펴보겠습니다.

Cost matrix에서 row, column 방향으로 값을 빼거나 더한 후 optimal matching을 찾는 것은 original cost matrix에서 optimal matching을 찾는 것과 동일하다.

Step 1: 행렬의 각 row에서 최솟값을 구한 후 빼준다.

0	17	42
15	0	40
0	26	128

Step 2: 행렬의 각 column에서 최솟값을 구한후 빼준다.

0	17	2
15	0	0
0	26	88

Step 3: 0을 가장 많이 포함하는 row line또는 column line을 최소 개수로 찾아준다. (볼드체)

0	17	2
15	0	0
0	26	88

Step 4: 찾은 개수가 행렬 크기 (n, 3×3이니 n=3)와 같다면, Step 6으로, 아니라면 Step 5로 이동 (여기서는 찾은 line은 2이니 즉 2 < 3, Step 5로 이동)

Step 5: 5-1) Step 3에서 찾은 라인으로 커버되지 않은 elements 중 최솟값을 찾는다. (커버되지 않은 볼드체가 아닌 영역에 대한 최솟값은 2)

5-2) crossed out이 아닌 row (여기서는 볼드체가 아닌 영역을 의미하겠죠)에 5-1에서 구한 최솟값을 빼준다.

-2	15	0
15	0	0
-2	24	86

5-3) crossed out column에 다시 최솟값을 더해준다. 5-2와 5-3은 곧 이미 찾은 optimal row line 및 optimal column line에는 변화를 주지 않겠다는 것을 의미합니다.

0	15	0
15	0	0
0	24	86

다시 Step 3로 넘어가서, optimal line을 찾습니다. 이번에는 3개의 line이 찾아졌으니, Step 6으로 넘어가도록 하죠. Step 6은 살짝 까다롭습니다.

Step 6. 각 row와 column에서 하나의 0만 가지는 조합을 찾은 후, original matrix에서 찾은 최적 조합의 위치를 적용한다. 즉, (3, 1) 위치의 0은 해당 row에서 혼자 0이니, (3,1)은 꼭 포함되어야하는 지점입니다. (3,1)을 포함하고 나면, (1,1)은 사용할 수 없고, 그렇다면 (1,3)을 반드시 포함하게 됩니다. 그렇게 된다면 다시 (2,3)을 포함할 수 없고, (2,2)가 선택이 됩니다. 결국 찾게된 optimal matching은 (1,3), (2,2), (3,1)이며, 해당 지점을 원래의 Cost matrix에 대입하면 122, 135, 150을 더한, 407의 비용이 최소 비용이 됩니다.

실제로 Brute Force로 찾아봐도 동일하며, 이러한 Hungarian algorithm (1999년도에 소개된 알고리즘입니다)을 사용하면 그 본질처럼 하나의 행, 즉 한 subset의 한 지점에 대한 minimum loss matching을 찾을 수 있게 됩니다. 중요하지 않다고는 말할 수 있으나 해당 알고리즘에 대해 아는 것 보다 그 알고리즘으로 해당 태스크를 수행할 수 있다는 것이 더 중요한데, 이야기가 잠시 샌 것 같습니다. 그럼 다시 돌아와서, 해당 알고리즘을 사용한 matching은 또한 permutation invariance를 보장하기 때문에, loss가 불변하다는 특성을 보장할 수 있겠네요. 아래를 보겠습니다.

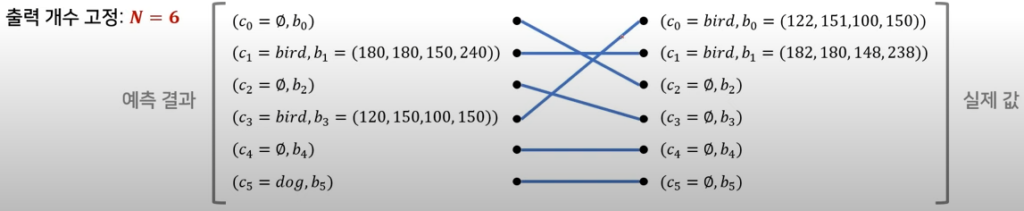
아래의 그림에서 c_0, c_1, c_2, ... 은 category label를, b_0, b_1, b_2, ... 는 bounding box offset을 의미합니다. 일대일로 매칭되어있고, 매칭이 잘되었다면 위의 그림과 같이 표현할 수 있겠네요. 그럼 학습을 위한 loss function 먼저 살펴봐야겠습니다. 매칭 시 pair-wise matching cost인 \mathcal{L}_{match}(y_i, \hat{y}_{\sigma(i)}) 을 살펴보겠습니다.

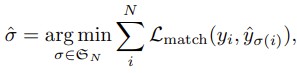
결국 위의 \mathcal{L}_{match}(y_i, \hat{y}_{\sigma(i)}) 를 통해 Hungarian algorithm을 효율적으로 계산할 수 있는 permutation \hat{\sigma} 을 찾는 것 입니다. 그렇다면 matching loss는 어떻게 구성될까요? 다음과 같습니다.

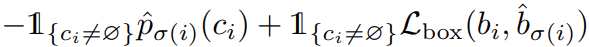
먼저 +를 기준으로 왼쪽의 -\mathbb{1}_{\left\{c_i \ne \varnothing\right\}} \hat{p}_{\sigma(i)} 는 클래스 예측 확률을 의미합니다. 다시 말해 permutation \sigma 의 i 번째 요소가 매칭되는 GT의 클래스를 예측한 확률을 의미하며, 확률값을 그대로 loss로 사용하기에 음수가 붙습니다. +기준 오른쪽의 -\mathbb{1}_{\left\{c_i \ne \varnothing\right\}} \mathcal{L}_{box}(b_i, \hat{b}_{\sigma(i)}) 은 bbox offset에 대한 예측 cost를 의미하며, 다시 말해 permutation \sigma 의 i 번째 요소가 매칭되는 GT의 클래스와의 좌표 간 loss를 의미합니다. bbox offset에 대한 loss라.. 해당 loss는 어떻게 구해질까요?

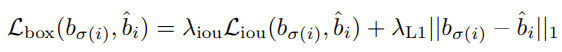
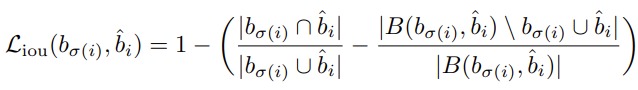
쉽지않아 보이네요.. 하지만 아래의 \mathcal{L}_{iou} 먼저 살펴보면, GIoU(Generalized-IoU)를 사용하고 있습니다. GIoU에 대해서 알고 계시겠지만, 다시 살펴보겠습니다. GIoU는 기존의 IoU를 통해 1-IoU를 loss로 사용하는 경우, 두 박스가 겹치지 않으면 해당 오차 수준을 알 수 없기 때문에 loss 계산이 제대로 되지 않습니다. 따라서 bbox와 GT를 모두 포함하는 최소 크기 박스를 설정하고, C box 영역에서 A와 B box의 합집합을 뺀 영역의 비율로 loss를 계산하면 됩니다. 그렇다면 결국 GIoU가 클수록 좋다는 의미입니다. 아래 그림을 보면 조금 이해가 쉬울 것 같습니다.

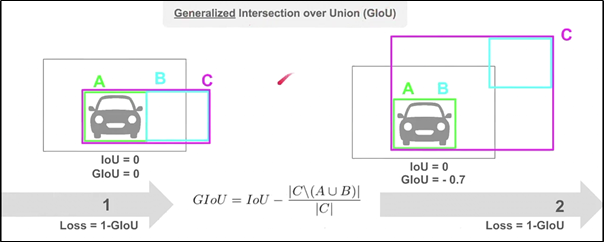
또한, GIoU를 사용하면 큰 물체와 작은 물체에 대한 bbox의 scale을 보정하는 효과가 있습니다. 다른 말로는, prior Anchor box가 없기 때문에 direct하게 예측한 bbox의 크기를 조금 더 잘 보정해주는 효과가 있습니다만, GIoU loss의 단점을 생각해보면.. box의 horizontal과 vertical에 대한 정보를 표현하고 있지 않으니 조금은 아쉽겠네요. 그리고서 L1 loss도 같이 사용합니다.

그렇게 그렇게해서 이제는 최종적인 loss를 살펴보겠습니다. 위에서 말한 loss가 끝이지 않나?라고 생각하겠지만, 아래의 수식을 보면,

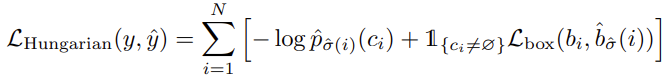
Hungarian loss는 클래스 확률에 대해 log를 씌어 계산합니다. 이는 사전에 설정한 object query의 수(여기서는 100)가 영상 내 object 수에 비해 훨씬 많으므로, 예측 클래스가 \varnothing 인 경우가 훨씬 많을테고, 그러한 imbalance를 해결하기 위함입니다. Faster R-CNN에서 sub-sampling과 유사한 효과를 보이겠네요.

자, 이렇게 Hungarian loss에 대한 설명이 마쳤습니다. Hungarian algorithm부터 시작해서, 해당 알고리즘에서 최적의 순열을 찾기 위한 (Step 5를 자주 안거칠수록 좋으니) matching loss를 구하는데, 이 때 loss는 클래스 확률과 bbox의 offset으로부터 계산된다고 보면 되겠습니다. 재밌는 점은, 그럼 모델 학습 중 backpropagation에 의해 조정되냐?하는 것은 아니겠죠. 왜냐하면 해당 loss는 matching cost를 줄이기 위한 loss로, 최적의 순열을 찾는 것은 Hungarian loss를 줄이는 역할을 하기 때문입니다. 그럼 이제는 모델의 Architecture를 살펴보며 Set prediction이라 말하면서 Set은 object query라고 했는데, 그러면서 object query는 또 뭔지, 살펴보겠습니다.

Architecture

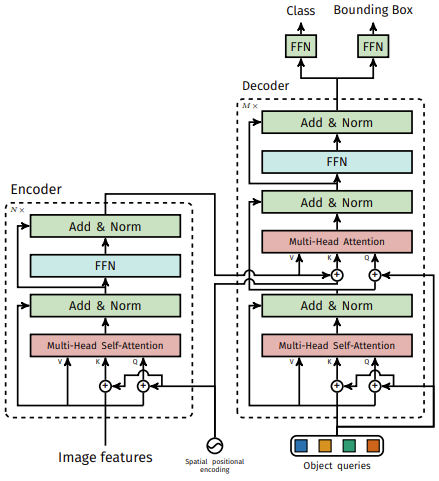
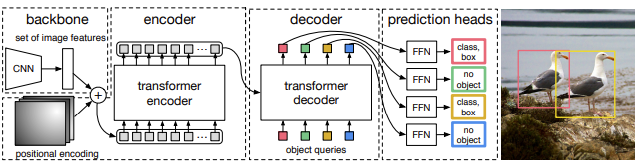
두 그림을 함께 이해하는 것이 좋을 것 같습니다. 우선 Transformer 구조는 워낙 익숙하실테니.. 넘어갈까 했지만 차이점을 살펴보겠습니다. 우선 image features라 함은 이미지 차원이 아닌 CNN Backbone을 통과한 feature map을 의미합니다. feature map을 transformer 입력 형태로 변환합니다. ( \mathbb{R}^{C \times H \times W} -> \mathbb{R}^{C \times HW} , 1×1 convolution layer를 통한 토큰 임베딩 차원으로의 flatten을 의미합니다.) 그

렇다면 결국 Self-Attention에서는 attention 메커니즘을 기반으로 Pixel-Pixel 간의 관계를 학습하게 됩니다. 그렇다면 Feature map 내의 모든 Pixel에 대해 attention 연산을 진행하니, global한 정보를 학습함과 동시에 연산량도 굉장히 많아질 것 입니다. 추가적으로 우리가 살펴볼점은 Multi-Head Self-Attention의 입력 시 Query와 Key에 대해서 Positional encoding을 더합니다. 이 때 코드를 살펴보면 sine positional encoding을 사용합니다.

다음은 Decoder입니다. Decoder를 살펴보면 object query가 있습니다. object query에 동일한 positional encoding을 더하냐하면.. 사실은 의미가 없습니다. 저자 Github issue에도 올라온것인데, decoder는 set, 즉 object query로 구성되어 있으므로 position이라는 것은 의미가 없죠. set의 성질을 다시 한번 상기시켜보면 이해가 갈 것입니다. Decoder의 첫 Multi-head attention에서는 object query간 관계를 학습합니다. 사실 해당 object query의 학습 가능한 positional encoding은 랜덤하게 초기화되기 때문에, 첫 Self-attention은 의미가 없다고도 볼 수 있습니다. 다음으로는 Encoder의 결과와 Attention 연산을 진행합니다. 이 때는 Encoder의 결과물과 query slot(object queries 중 하나를 query slot이라 명합니다.) 간의 attention 연산으로 어느 query가 어떤 위치에서 object를 찾을 수 있을지를 학습합니다.

이렇게 통과하고 나면 우리는 최종적으로 두개의 FFN을 거쳐서 각각 Class와 Bounding Box에 대한 query들을 얻을 수 있죠. 다시 위의 글로 돌아가서 학습에서는 Backpropagation을 거치지 않는다고 했는데, 어떻게보면 FFN 결과로 나온 class와 bbox offset으로 구성된 query slot을 최적의 매칭을 거치니, Transformer 학습 과정에서 Backpropagation을 거치지 않는다고 볼 수 있으니 그렇게 말했습니다. 말을 아무리 풀어보려했는데.. 이해가 되셨을지는 모르겠네요. 최종적으로는 query slot들과 gt간 bipartite matching을 통하여 detection을 수행합니다. 아래의 그림을 보고서 조금 더 이해가 되셨으면 좋겠습니다.

이제 전체 파이프라인이 마쳤습니다. 실험 결과를 통해 조금 더 살펴보고 이해를 도울 부분이 있는지 지켜보겠습니다.

Experiments

비교 대조군은 Faster-RCNN으로, COCO 2017 dataset (평균적으로 하나의 이미지 내 7개의 object들이 있으며, 충분히 떨어져 있습니다) 에서 이루어졌습니다. Architecture, loss 등의 Ablation study로 자세히 살펴보며, 추가적으로 DETR 모델의 확장성 (이는 Transformer 기반 모델들은 확장성에 꽤나 초점이 맞춰져있는 느낌이 듭니다)을 보고자 panoptic segmentation에 대한 성능도 보이고 있습니다. 실험 결과로부터 어떤 고찰을 얻을 수 있을지 기대가 되네요. 한번 보도록 하겠습니다.

• Technical details

리뷰에서 보통은 해당 내용을 다루지 않는데, 이번에는 아래 표에서의 설명을 위해 짚고 넘어가겠습니다. 먼저 논문만 보자면 AdamW를 쓰고, learning rate는 어떻게 조절했다..는 내용등이 있지만, 우리가 살펴봐야할 점은 Resnet50과 Resnet101을 Backbone 네트워크로 사용했다는 점입니다. Resnet이 중요한 것이 아니라, ViT 기반이 아닌 CNN Backbone에서 추출한 Feature map을 사용한 것을 다시끔 상기할 수 있습니다. 각각은 DETR과 DETR-101이라고 명하네요.

다음으로는 Feature resolution을 올리기 위해 dilation을 백본 마지막에 추가했는데, 이를 각각 DETR-DC5와 DETR-DC5-R101이라고 명합니다. Feature resoltuion, 쯕 receptive field를 늘린 이유에 대해서는 small object에 대한 성능을 잡고자함이라고 설명하는데, Self-attention 과정에서 연산량이 늘어나 전체적으로 computational cost가 2배 정도 늘었다고 설명합니다. 또한 Random crop augmentation 방법을 사용하여 object specific한 정보를 더욱 학습하고자 한 것으로 보이는데, 1AP의 성능 향상을 보였다고 합니다. 또한 obejct query의 slot이 예를 들어 한 이미지 내 5개의 object가 있다고 할 때, 전체 slot이 100개라고 하면 95개나 되는 수의 slot이 empty class를 가지기 때문에, AP 향상을 이루기 위하여 2번째로 높은 스코어 클래스에 한번 부여해보는 방식을 사용했으며, 이는 2 AP의 성능향상을 보였다고 합니다.

마지막으로 재밌는 점으로 300 epoch 학습하며 16개의 V100에서 각각 4배치 사이즈로 (전체 배치 64) 3일정도의 training time이 걸렸다고 합니다. 굉장한 수준의 training cost네요. Faster R-CNN과 비교를 위해 500 epoch 학습했을 때는, 또 1.5 AP의 성능 향상을 보였다는 점도 흥미롭습니다. 디테일한 부분에서의 조정으로 좋은 성능을 보이도록 스케쥴링한 모습이 눈에 띕니다. 그렇다면 바로 Faster R-CNN과의 성능 비교 표를 살펴보겠습니다.

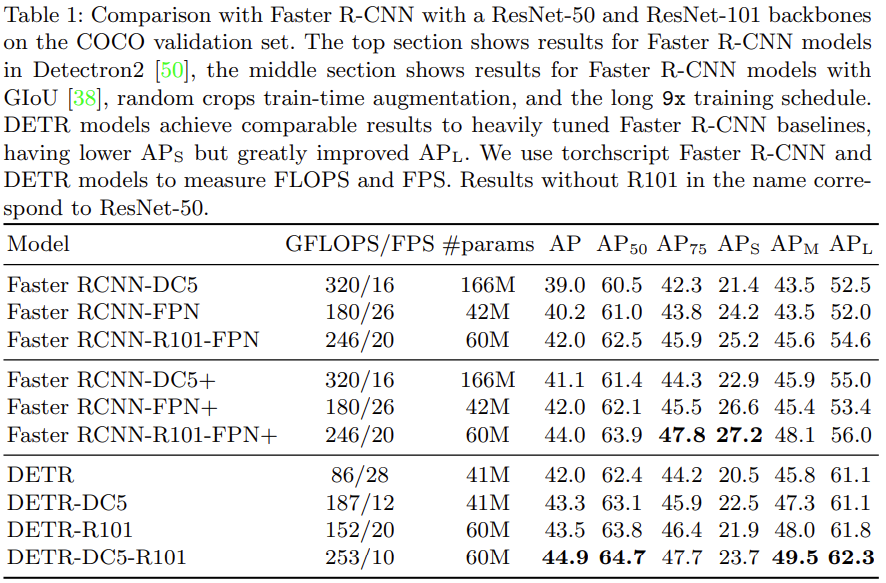
위의 표에서 Faster RCNN-DC5는 Dilated convolution을 추가한 버전으로, Faster RCNN-DC5+에서 +는 GIoU와 Random crop augmentation. 그리고 training schedule을 길게 가져갔을 때의 결과입니다. DETR이 GFLOPS는 전체적으로 떨어지지만, parameter 수들은 생각보다 적은 것을 알 수 있습니다. 아마 이 점은 Faster RCNN에서 RPN을 거치면서 연산량이 많을 수 밖에 없는데, direct set prediction으로 접근하였기 때문이라고 봅니다. AP, AP50 AP75에서의 성능을 보면 전반적으로 동일 선상에서의 비교 시 약 1-2% 정도 향상된 성능을 보입니다. 재밌는 점으로는.. FPS가 많이 떨어지네요. 해당 부분은 Real-time detection 측면에서는 꽤나 문제가될 수 있는데, 아무래도 Transformer Enc-Dec block을 8번이나 반복한다는 점에서.. 아쉬운 측면 같습니다.

추가적으로 크기 측면에서 보자면 AP_L에서는 성능 향상이 많이 일어난 것을 확인할 수 있습니다. 이는 당연히 attention 연산에서 기인한 결과라고 확인할 수 있겠지만, AP_S, 즉 작은 물체에 대해서는 성능이 4% 정도 떨어지는 것을 볼 수 있습니다. 이는 CNN Backbone을 통과한 마지막 단의 feature map을 사용하기 때문에, receptive field 측면에서 작은 물체에 대한 인식이 떨어진다고 볼 수 있습니다. 아마 이 점으로 저자들은 multi-scale, 즉 FPN과 같은 기법을 사용 시 성능 개선이 일어날 것이라고 분석합니다. (이는 제가 다음 번에 리뷰할 Deformable DETR에서 다시 살펴보겠습니다). 다음은 Encoder size에 대한 성능 결과입니다.

• Ablation study

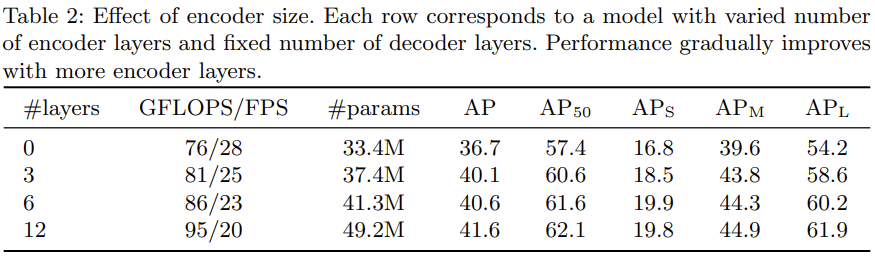
layer 0의 Encoder를 사용하지 않는 경우는.. 사실 논문에서 말하고자하는 바와는 맞지 않는 것 같지만, 결국 하고 싶은 말은 Encoder는 attention 연산으로 이미지 내 물체를 분리하는 데에 중요한 역할을 한다, 다른 말로는 이미지 내 물체가 있을법한 위치를 Decoder에 효과적으로 알려줘서 object query가 적절한 object를 찾고자하는 역할을 한다고 봅니다. 결국 Attention이 중요하다는 말을 하는데, Attention map을 통해 Encoder에서부터 물체를 잘 분리하고 있고, 따라서 Encoder에서 학습된 임베딩을 Key, Value로 사용하는 Decoder가 detection을 잘 할수 있도록 도움을 준다고 해석 하면될 것 같습니다. 물체를 효과적으로 분리한다는 것은 아래의 그림을 보면 조금 더 이해가 쉽겠네요. 또한 살펴볼점은, Encoder를 사용하지 않을 때는 AP_L 에 대한 성능이 큰 보폭으로 떨어지는 모습도 살펴볼 수 있습니다.

다음은 Decoder입니다.

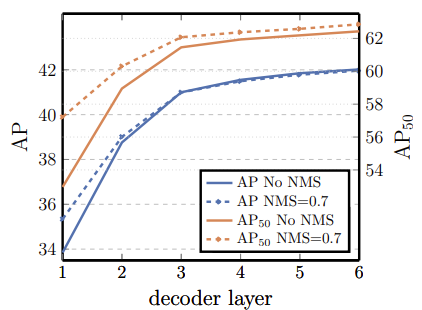
Decoder layer가 깊어질수록 (많아질수록) AP가 높아지는 모습이 보이며 Bipartite matching을 통해 물체를 분류하기 때문에, 또한 Decoder가 object들 간의 관계를 잘 학습할 수 있기 때문에 (아래의 코끼리와 얼룩말 사진을 보시면 잘 분류하는 모습을 볼 수 있습니다), NMS를 추가하여도 성능 향상이 없는 모습을 볼 수 있습니다. 왜 Direct set prediction이 가능한지에 대한 고찰로도 볼 수 있겠네요.

또한, 코끼리와 얼룩말 사진을 토대로 attention map을 시각화한 결과를 살펴보면, Decoder는 detection 학습 과정에서 object의 말단 부분인 가장 자리에 큰 attention을 주도록 학습되기 때문에 occlusion에도 강인한 모습을 볼 수 있습니다.

즉 encoder와 decoder 결과를 통해 우리는 encoder가 global attention을 통해 이미지 내 물체를 잘 나누도록 학습한 다음, decoder는 클래스 및 물체의 가장자리 부분을 통해 정확한 bbox를 추출하도록 attention을 주도록 학습하는 모습을 확인할 수 있습니다.

다음은 object query에 대한 시각화 자료인데, 빨간색과 파란색, 초록색은 각각 수평으로 큰 bbox, 수직으로 큰 bbox, 작은 bbox를 나타냅니다. 해당 그림도 좋지만 아래의 그림을 보면 더욱 이해가 쉬울 것 같습니다. 결국 하고 싶은 말은, 각 object query마다 이미지의 특정한 부분 및 박스 크기에 대해 예측을 수행하며, 학습된 query가 object의 위치에 따라 그에 상응하게 반응하여 활성화되고 있는 모습을 볼 수 있습니다. 아래의 그림에서 색상으로 점이 있는 부분이 object query이니, 이 점을 기반으로 참고하시면 좋을 것 같습니다.

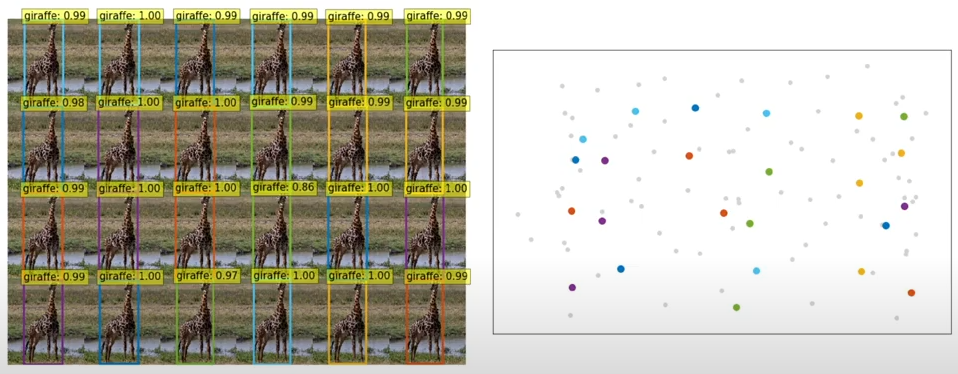
실제 ECCV oral에서 사용한 Encoder, Decoder, 그리고 object query의 시각화 자료를 살펴보면 완벽한 이해가 되리라 기대합니다. object query가 물체의 이동에 따라 같이 움직이는 모습이 인상적이네요. 직접 편집했는데.. 다음 번엔 워터마크 없는 버전으로 해보겠습니다.

마지막으로는 확장성을 보고자, panoptic segmentation에서의 결과입니다. panoptic segmentation이란 이미지 내의 모든 픽셀을 class로 분류하는 semantic segmentation과, 동일한 클래스 내 서로 다른 객체를 구분하는 instance segmentation이 합쳐진 개념으로, DETR의 decoder에 mask head를 추가하는 방식 (Faster R-CNN에 mask head를 더해만든 Mask R-CNN 구조와 동일)으로 태스크를 진행합니다.

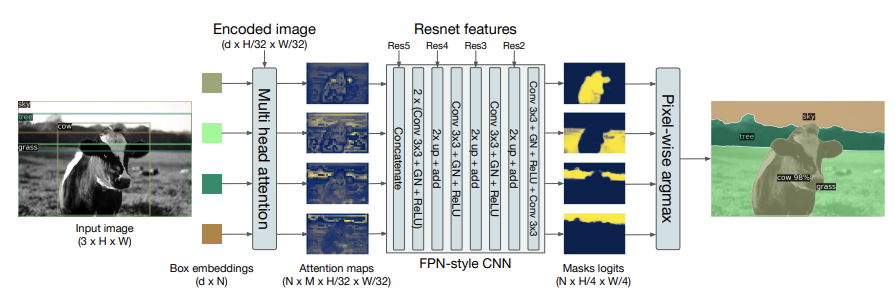
위의 그림을 보면, 왼쪽에 보이는 Decoder의 결과물을 다시 Encoder의 Feature map과 attention 연산을 통해 attention map을 생성합니다. 하지만 해당 attention map은 화질이 좋지 않아 (coarse),Backbone에서 저장해놓은 Feature map과 upsampling + add를 통해 high resolution의 masks logits를 만들어내고, pixel-wise argmax를 통해 panoptic segmentation을 수행합니다.

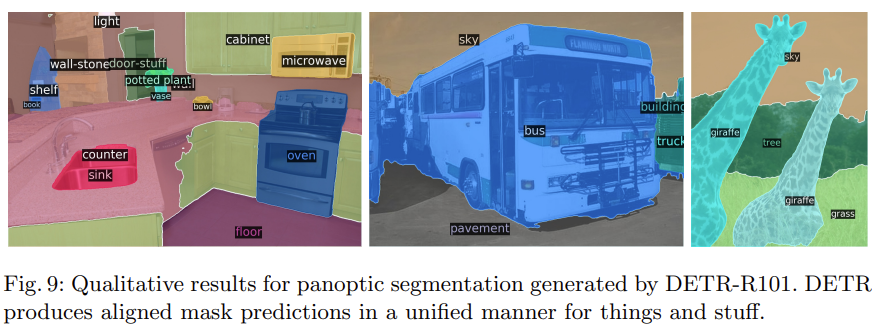
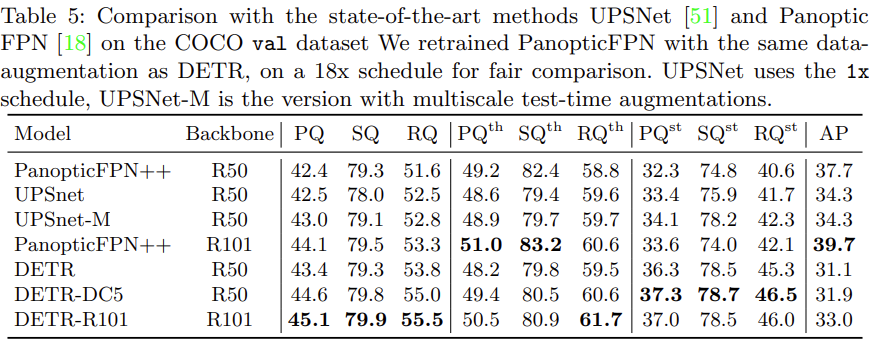
성능에서는 Panoptic Quality 기준 당시 Sota 모델인 PanopticFPN을 넘는 성능을 기록하였습니다. 특히, sky, tree와 같은 stuff는 다른 모델 대비 훨씬 높은 성능을 기록하였으며, 저자는 이에 대해 encoder attention의 global information이 좋은 영향을 끼쳤을 것이라고 보고 있습니다.

Conclusion

왜 작은 물체에서의 성능이 안좋은지에 대해 생각해보고, 추가적으로 ViT가 아닌 Transformer 기반의 방식을 사용하였다, GIoU를 사용하였다 등등 자세히 뜯어보면 정말 많은 내용들이 있지만, 가장 중요한 점은 Direct set prediction을 통해 prior knowledge가 필요하지 않았다는 점을 중요시 여겼으면 좋겠습니다.

이번 리뷰는 여기서 마치겠습니다. 감사합니다.