Before Review
제가 이 논문 리뷰 part.1을 두 달전 쯤에 작성했는데 갑자기 생각이 나서 이제 마무리를 지으려고 합니다..
아쉬운 건 코드를 공개하겠다고 했는데 공개를 안 했네요. 저자들이 한국인이라 메일을 보내볼까 생각하고 있습니다.
리뷰 시작하도록 하겠습니다.
Method
지난 Part.1 리뷰 내용의 일부를 발췌하도록 하겠습니다.
Probabilistic Video Embedding
논문의 핵심은 video feature를 deterministic 하게 vector로 embedding 하는 것이 아니라 가우시안 분포로 embedding 시킨다는 것입니다.
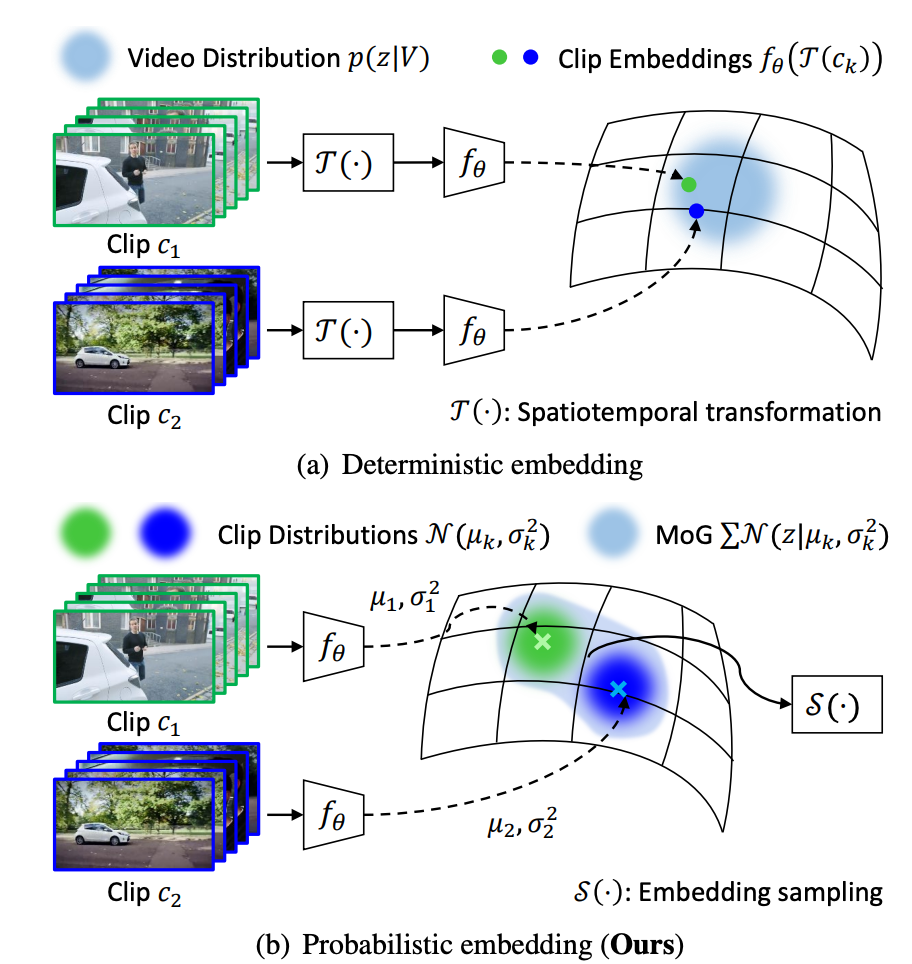
위의 그림을 보면 Deterministic의 방식은 Clip을 3D encoder를 태워 단순히 embedding space 내부에 존재하는 하나의 vector로 mapping 시키는 것입니다. 하지만 Probabilistic 방법은 mean vector와 covariance matrix를 찾는 과정 입니다. embedding space 내부에 존재하는 하나의 확률 분포로 근사 시킬 수 있습니다. 즉, 가우시안 분포로 embedding을 시킨다는 것은 결국 평균과 공분산 행렬을 잘 찾는 과정이라 보면 됩니다.
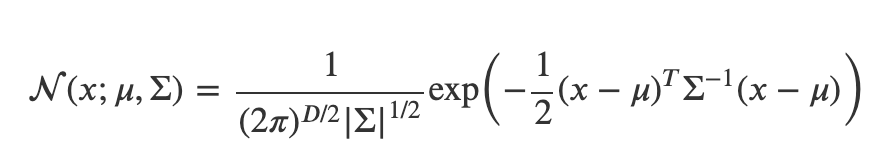
데이터를 가지고 가우시안 분포를 결정할 때는 보통 최대우도법(MLE)을 사용하지만 여기서는 신경망을 이용하여 평균 벡터와 공분산 행렬을 구할 수 있는 함수를 모델링 합니다.
- \mu =g_{\mu }\left(v_{c_{n}}\right)=L_{2}Norm(LayerNorm(FC\left(v_{c_{n}}\right)))\in R^{D}
- \sum=diag\left(g_{\sigma}\left(v_{c_{n}}\right)\right)=diag\left(FC\left(v_{c_{n}}\right)\right)\in R^{D}
여기서 평균 벡터와 공분산 행렬을 추정할 때 사용되는 FC layer는 parameter를 공유하지 않습니다.
그리고 난 다음에 N개의 클립에 대해서 위와 같은 과정을 반복하면 일단 N개의 가우시안 분포를 추정할 수 있습니다. 이제 우리는 단일 비디오에 대해서 비디오에 대한 혼합 분포를 가우시안 혼합모델로 결정합니다.
- p\left(z\mid V\right)=\sum^{N}_{n=1} N\left(z;g_{\mu}\left(v_{c_{n}}\right),diag\left(g_{\sigma}\left(v_{c_{n}}\right)\right)\right)
비디오에 대해서 혼합 분포를 추정하고 난 다음에는 K개의 새로운 embedding feature를 생성합니다. 이때 새로운 embedding feature를 생성하는 방법은 아래와 같습니다.
- z^{(k)}=\sigma(V)\odot \epsilon^{(k)}+\mu(V)
여기서 \epsilon^{(k)}은 가우시안 분포로 독립 항등 방식으로 샘플링된 random vector 입니다. 그리고 \sigma(V)\, \mu(V)는 각각 p\left(z\mid V\right)의 평균과 분산 입니다. 결국 하나의 비디오를 설명할 수 있는 혼합 분포가 있고 이 혼합 분포의 평균과 공분산이 존재할 때 평균과 분산을 조금씩 바꾸어가며 K개의 새로운 embedding feature를 생성한다는 의미입니다.
Mining Positive and Negative Pairs
Deterministic representation 과는 다르게 probabilistic representation을 위해서는 euclidean distance가 아니라 probability distance를 가지고 embedded distribution과의 유사도를 계산합니다. 여기서 사용하는 지표가 Bhattacharyya distance를 사용한다고 합니다. 두 연속확률 분포의 유사도를 비교할 때 평균과 분산을 동시에 고려한 지표라고 생각하면 됩니다. 아래와 같이 정의 됩니다.
- dist\left( z^{(k)}_{i},z^{(k^{\prime })}_{j}\right) =\frac{1}{4} (\log \left( \frac{1}{4} \left( \frac{\sigma^{2}_{i} }{\sigma^{2}_{j} } +\frac{\sigma^{2}_{j} }{\sigma^{2}_{i} }+2\right)\right))+\lambda \cdot \frac{\left( z^{(k)}_{i}-z^{(k^{\prime })}_{j}\right)^{T} \left( z^{(k)}_{i}-z^{(k^{\prime })}_{j}\right) }{\sigma^{2}_{i} +\sigma^{2}_{j} }
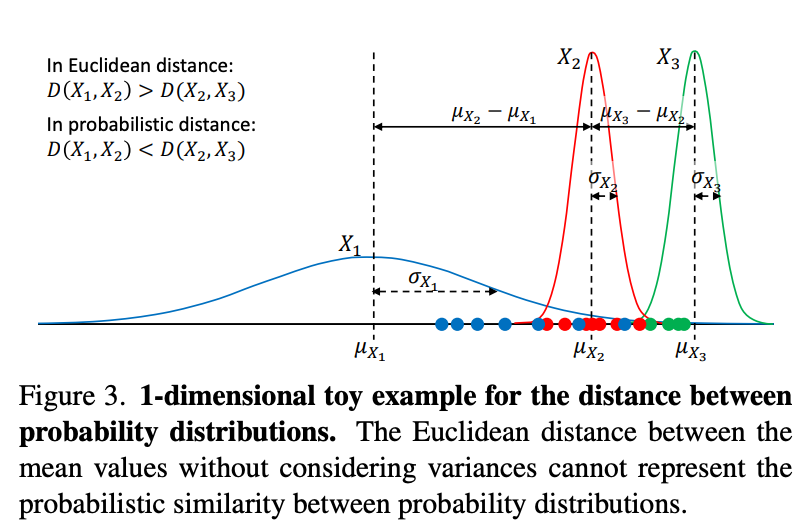
여기서 분포를 보면 X_{1}, X_{2} 그리고 X_{3}이 있습니다. X_{1}과 X_{2} 간의 유사도와 X_{2}과 X_{3} 간의 유사도는 뭐가 더 높을까요? 모양이 비슷하게 생겼다고 해서 유사도가 높은 것이 아니라 겹치는 영역이 더 많아야 유사하다고 볼 수 있습니다.
X_{2}는 X_{1}과 겹치는 구간이 더 많기 때문에 X_{3}에 비해 X_{1}과 더 유사하다고 볼 수 있습니다. 그런데 보통 많이 사용하는 평균간의 Euclidean distance는 이러한 유사도 관계를 보장해주지 못합니다. 따라서 저자는 Bhattacharyya distance를 통해 평균과 분산을 동시에 고려하여 두 확률 분포간의 유사도를 정의합니다.
위에서 설명한 거리는 클립으로 부터 정의되는 가우시안 분포간의 유사도를 측정하는 방법이며 이제는 비디오 간의 유사도를 측정하는 방법을 정의하겠습니다. 위에서 비디오를 가우시안 혼합 모델로 정의하고 이를 다시 reparameterization을 통해 K개의 stochastic embedding feature를 계산한다고 했습니다.
그리고 두 비디오로 부터 K개의 stochastic embedding feature를 일대일 대응 방식으로 거리를 비교하고 평균내는 방식으로 비디오간 유사도를 측정하고 있습니다.
- dist(V_{i},V_{j})\approx \frac{1}{K^{2}} \sum^{K}_{k} \sum^{K}_{k^{\prime }} dist\left( z^{(k)}_{i},z^{(k^{\prime })}_{j}\right)
비디오간 이제 positive, negative 관계는 임계치 처리를 통해 얻어집니다.
- P=\{ \left( V_{i},V_{j}\right) \mid dist(V_{i},V_{j})<\tau \}
비디오간 유사도를 통해 threshold \tau 보다 작은 비디오들을 positive로 정의합니다. 당연히 negative는 그 반대겠네요. 이제 이 pair를 통해서 stochastic contrastive loss를 통해 학습을 진행합니다.
Stochastic Contrastive Loss
제안하는 방식으로 distance를 구하고 비디오간 유사도를 통해서 비디오 끼리 positive, negative를 구성했습니다. 이때 우리는 deterministic 하게 embedding 한 것이 아니라 stochastic 하게 embedding을 했기 때문에 우리가 평소에 사용하던 InfoNCE Loss는 사용할 수 없습니다.
하지만 목적 자체는 비슷하겠죠. 서로 positive pair 관계에 있는 비디오 들은 그 비디오를 구성하는 가우시안 분포들끼리 서로 유사해지게 만드는 것 입니다.
하지만 위에서 만든 pair는 분명히 noise 합니다. Positive pair라고 계산 됐지만 실제로는 negative의 관계일 수 있고, 그 반대도 역시 발생할 수 있습니다.
따라서 이러한 uncertainty에 대해서 penalty를 주기 위한 장치도 필요합니다. 즉, 제안되는 Loss 함수는 일단
- probabilistic distance 기반으로 정의되는 pair를 바탕으로 contrastive learning을 수행할 수 있어야 합니다.
- 동시에 uncertainty가 높은 두 비디오의 상황에서는 앞선 (1)의 영향력을 줄여야 합니다.
무슨 말인지 조금 애매할 수 있으니 이제 수식적으로 접근해보도록 하겠습니다.
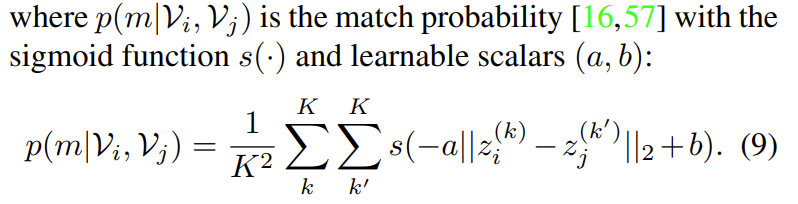
일단 서로 다른 두 비디오간의 match probability 부터 계산하는 방식에 대해서 살펴보도록 하겠습니다.
앞서 z^{(k)}는 z^{(k)}=\sigma(V)\odot \epsilon^{(k)}+\mu(V) 이렇게 정의된다고 했었습니다. GMM을 통해서 얻은 video representation의 self-augmented embedding 입니다. 비디오마다 K개의 embedding을 sampling 했기 때문에 수식을 보면 O(K^{2})의 복잡도를 가지고 있습니다.
결국 s(-a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b)을 K^{2}번 더하고 평균 내주고 있습니다.
- s는 sigmoid 함수 입니다. 어떤 값이 입력으로 들어오든 일단 0~1사이로 변환하여 줍니다.
- a와 b는 학습 가능한 parameter 입니다. 자세한 이유는 나와있지 않지만, 아마도 sigmoid 함수를 사용할 때 너무 saturation 되는 것을 방지하기 위해 사용하는 것 같습니다.
- \left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}은 sampling된 embedding 끼리의 Euclidean distance 입니다.
우리가 원하는 상황을 가정해보겠습니다. Positive/Negative pair가 잘 구성되었고 GMM을 통해 Video distribution이 잘 생성되었기를 바라고 있겠죠.
이는 서로 Positive 관계에 있는 두 비디오로부터 나온 augmented embedding들은 유사한 표현력을 가져야 함을 의미합니다. 또한 Negative 관계에 있는 두 비디오로부터 나온 augmented embedding들은 유사하지 않은 표현력을 가져야 함을 의미합니다.
따라서 Loss 함수는 아래와 같이 설계되어야 합니다.
Positive Pair
- Positive 관계에 있는 비디오는 \left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}는 작아지는(0으로) 방향으로 학습되어야 합니다.
- 이는 -a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b가 b에 가까워지는 방향입니다.
- b가 적당히 큰 값으로 수렴되면 sigmoid 함수 개형에 따라 s(-a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b)는 1에 수렴하게 됩니다.
Negative Pair
- Negative 관계에 있는 비디오는 \left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}는 커지는(무한대로) 방향으로 학습되어야 합니다.
- 이는 -a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b가 음의 무한대에 가까워지는 방향입니다.
- -a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b가 음의 무한대에 가까워지면 sigmoid 함수 개형에 따라 s(-a\left|z_{i}^{(k)}-z_{j}^{(k)} \right|_{2}+b)는 0에 수렴하게 됩니다.
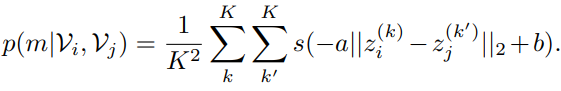
결국 위에서 정의 되는 matching probability p(m|V_{i},V_{j})는 Positive Pair에 대해서는 1로 수렴하고 Negative Pair에 대해서는 0으로 수렴합니다.
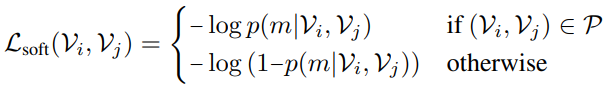
그리고 위의 soft contrastive loss를 보면
- Positive Pair에 대해서는 -log(p(m|V_{i},V_{j}))가 작아져야 하니, p(m|V_{i},V_{j})가 1로 수렴하는 방향을 가지고 있습니다.
- Negative Pair에 대해서는 -log(1-p(m|V_{i},V_{j}))가 작아져야 하니, p(m|V_{i},V_{j})가 0으로 수렴하는 방향을 가지고 있습니다.
정확히 우리가 원하는 방향과 일치합니다. 하지만 여기서 고려 해야 할 것이 하나 있습니다. Probability Distance로 정으한 Positive/Negative Pair가 불안정할 수 있다는 것입니다. GMM을 구성하는 각 가우시안 분포의 통계치를 학습하는 구조이기 때문에 당연히 노이즈가 생길 수 있습니다.
이를 방지 하기 위한 regularization 아이디어는 아래와 같습니다.
“Positive Pair라 할지라도 두 비디오 분포의 편차가 크다면, soft contrastive loss의 영향력을 줄이고 두 비디오의 편차를 줄이는 방향으로 학습하자.”
무슨 말인지 애매하니 다시 수식으로 보도록 하겠습니다.
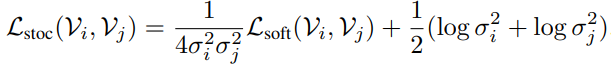
L_{soft}에 두 비디오 분포의 편차가 곱이 역수로 곱해져있습니다. 두 비디오 분포의 편차가 크면 분모가 커지고 Loss의 크기가 작아져 학습에 영향력이 줄어들겠죠.
두 비디오 분포의 편차가 큰 상황에서는 \frac{1}{2}(log(\sigma_{i}^{2})+log(\sigma_{j}^{2})))가 큰 값을 가지게 되고 이를 작아지게 하는 방향으로 학습이 되니, 편차를 줄이는 방향으로 학습 됩니다.
이렇게 정의되는 stochastic contrastive loss는 결국 positive pair라 할지라도 편차가 큰, uncertainty가 큰 상황을 control하기 위한 regularization term까지 고려하여 정의가 됩니다.
Total Objectives
추가적인 KL regularization term 까지 정리하고 total loss 함수를 정리하도록 하겠습니다. 비디오 분포를 학습 하는 과정에서 covariance matrix가 0으로 붕괴되는 것을 방지하기 위한 regularization term을 추가했다고 합니다.
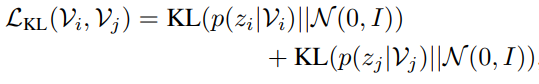
위의 regularization term을 통해 비디오의 분포가 평균이 0이고 공분산 행렬이 단위행렬인 정규분포와 비슷해질 수 있습니다. 아마 이 regularization은 강하게 할 것 같지는 않습니다. Implementation detail을 찾아보니 \beta는 10^{-4}을 사용한다고 하네요.
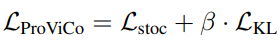
최종 Loss는 위와 같습니다.
Experiments
Action Recognition
Linear evaluation on Kinetics-400
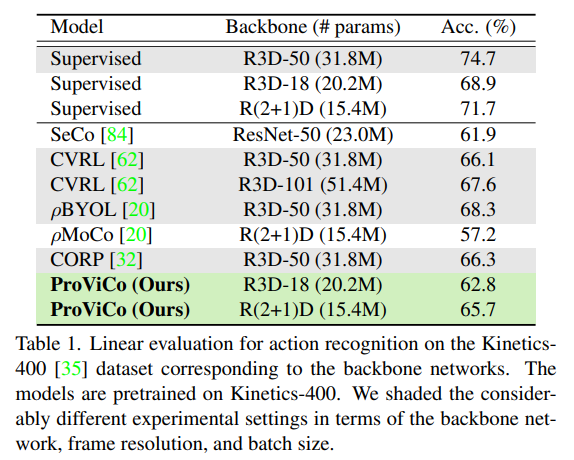
Kinetics-400에서의 Action recognition linear evaluation 입니다. Linear evaluation은 사전학습된 백본은 고정시키고 마지막에 linear layer만 다시 학습 시키는 것입니다. 아래 테이블에서 회색으로 칠해진 방법론들은 백본의 크기가 다르기 때문에 직접적인 비교는 어렵고 하얀색으로 칠해진 방법론들과 비교하면 됩니다.
대표적으로 21년도 CVPR에 나온 방법론인 \rho MoCo와 비교했을 때 동일한 백본 대비 Linear evaluation 성능을 8.5%나 향상 시켰습니다.
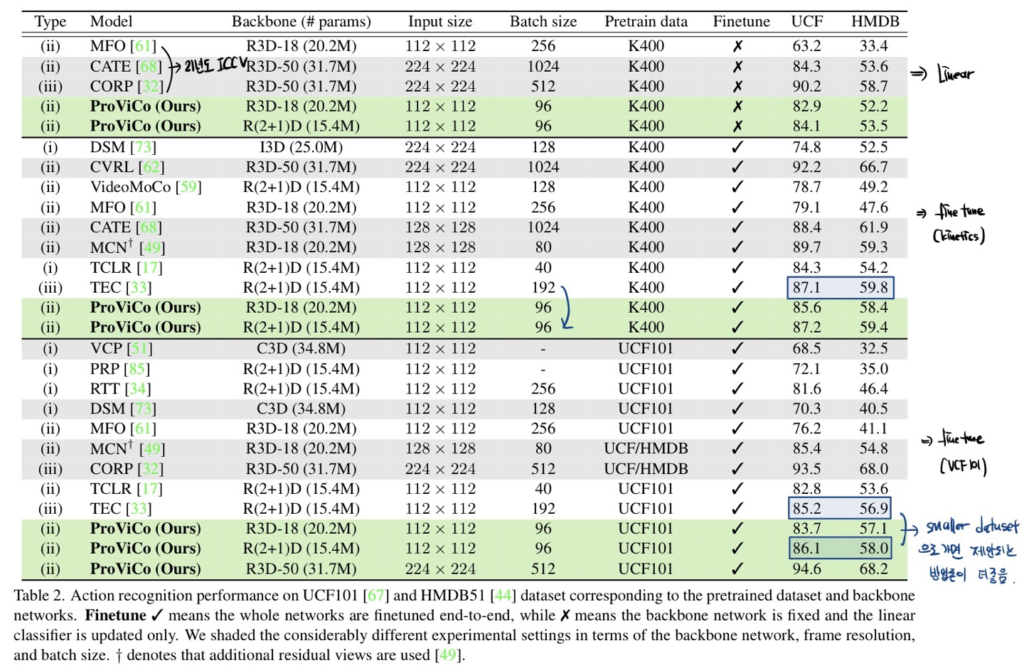
Linear evaluation on UCF101 and HMDB51

위에 보이는 MFO, CATE, CORP는 모두 21년도 ICCV에 발표된 연구들입니다. 본 논문에서 제안하는 ProViCo는 더 적은 배치 사이즈와 입력 사이즈를 가져가면서도 우수한 성능을 보여주고 있습니다.
Finetuning on UCF101 and HMDB51
일단 테이블의 두번째 단락을 보면 Kinetics-400으로 finetuning 시켰을 때의 성능입니다. 회색 라인은 사실 fair comparison이 아니기 때문에 큰 의미는 없고 두 번째 단락에서 TEC라는 방법론과 비교하면 동일 백본 대비 더 적은 배치사이즈를 가져갔을 때 비슷한 성능을 보여주고 있습니다.
다음으로 테이블의 세번째 단락을 보면 UCF101, HMDB51과 같은 더 작은 데이터 셋으로 finetuning 시켰을 때의 성능입니다. 동일하게 TEC라는 방법론과 비교하면 더 적은 데이터 셋에서는 제안되는 방법론이 더 우수함을 보여주고 있습니다.
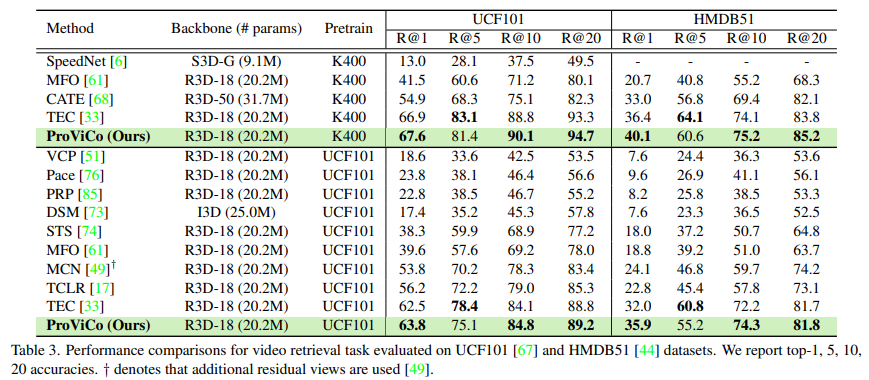
Video Retrieval
Video Retrieval에서도 벤치 마킹을 진행했습니다. 제안되는 probablistic approach가 matching task에서도 좋은 표현을 학습 시킨다고 주장하고 있네요. 다만 의아한게 Recall@5에서만 성능이 조금 떨어지네요..?
Ablation Study and Analysis
Ablation을 다룰 예정인데 단순 hyper-parameter 에 대한 실험은 크게 의미가 없는 것 같아 리뷰에는 제외했습니다.
저자는 학습 과정에서 uncertainty와 discriminability of representation 간의 관계를 분석하였습니다. 실험은 Video Retrieval에 대해서 진행했다고 합니다.
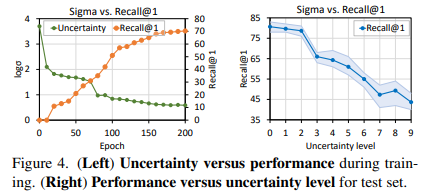
학습 과정 중 10epoch 마다 모든 비디오의 uncertainty를 평균 내고 Recall@1를 평균 냈습니다. 아래 그림 중 왼쪽의 그래프를 보면 accuracy는 올라가면서 uncertainty는 낮아지고 있습니다. 근데 사실 이건 당연한 결과일 수 밖에 없는것이 loss term 중 uncertainty에 대한 regularization을 넣었기 때문에 uncertainty는 무조건 낮아지는 것이 아닌가 생각이 드네요.
오른쪽 그래프는 uncertainty level을 일부러 강하게 했을 때 Recall이 떨어지고 있습니다. 이를 토대로 performance와 uncertainty 간의 negative correlation이 있다고 주장합니다.
Main Paper에서 다루는 ablation은 이게 끝인데 개인적으로는 Loss 함수에 있는 uncertainty에 대한 regularization term에 대해서 ablation이 무조건 있었어야 하지 않나 싶습니다. 뭔가 좀 찜찜한 기분이 드네요.
Conclusion
개인적으로 비디오 클립을 하나의 feature vector로 임베딩 시키는 것이 아니라 probability distribution으로 매핑 시킨 아이디어 참신했던 논문이었습니다. 저자가 밝히는 본 논문의 한계는 바로 Untrimmed Video의 상황입니다. 더욱 더 data uncertainty가 커지고 background의 영향을 받기 때문에 Untrimmed video의 상황에서도 확률적인 접근을 통해 positive/negative pair를 잘 구성하는 것이 future work라 밝히고 있습니다.
코드를 참고하고 싶은 부분이 있어 저자에게 메일을 보내려고 합니다. 분명 appendix에는 paper release 다음에 공개한다고 적혀있었는데..
리뷰 마무리하도록 하겠습니다. 감사합니다.