[CVPR 2018] Non-local Neural Networks

Introduction

convolution은 연산 방식이 일정 크기의 커널을 이미지에 windowing하면서 연산을 진행하기 때문에, local한 관계에 집중합니다. 그러다 보니 [ 그림1 ]과 같이 멀리 떨어진 픽셀은 좀 더 많은 레이어를 통과한 이후에나 관계를 파악할 수 있습니다. 이렇듯 멀리 떨어진 특징끼리는 그 사이의 관계를 파악하기 어려운 것을 long range dependency라고 합니다.

음성, 언어(텍스트)와 같이 데이터가 순서에 영향을 받는 시계열 데이터는 rnn모델을 주로 사용합니다. rnn에서 사용되는 회귀 연산은 이러한 long range dependency를 해결할 수 있습니다.

rnn은 recurrent 연산을 수행하는데, 시계열 데이터인 텍스트를 한 단어씩 순차적으로 입력합니다. 이때 하나의 문장을 입력하면 첫 단어인 what에는 레이어의 초기 가중치를 곱하고, 그 다음 단어인 time에는 이전 단어 ‘What’에 가중치 W를 곱함으로써 생성된 hidden state를 가중치로 사용합니다. 이처럼 한 번의 recurrent연산에서는 모든 입력 요소간의 연산을 진행하기 때문에 rnn은 long range dependency를 해결할 수 있습니다.

시계열 데이터가 아닌 이미지의 경우, 전체 이미지를 고려하기 위해, 즉, 넓은 receptive field를 갖기 위해 레이어를 깊게 쌓아 반복적인 convolution연산을 수행합니다. [ 그림 2 ]에서 볼 수 있듯 convolution을 수행하여 출력된 값은 이전 이미지에서 kernel size만큼의 영역을 고려한 값이라고 할 수 있습니다. 따라서 convolution연산을 많이 수행할수록, 출력된 특징값은 처음 입력된 이미지의 넓은 영역을 파악할 수 있습니다.

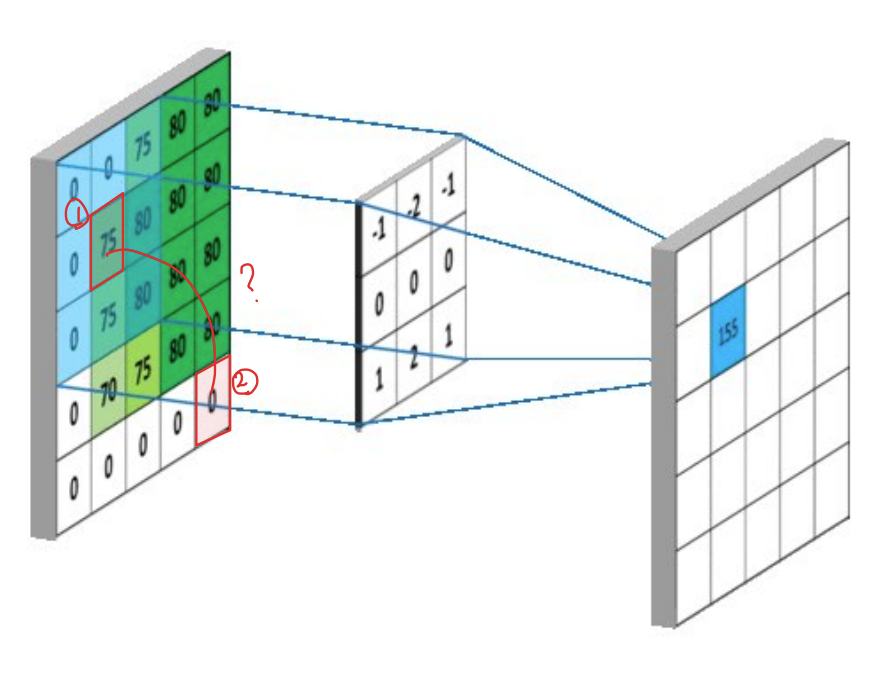
그러나 이러한 local 연산을 반복적으로 사용하면 연산 네트워크의 깊이가 증가하여 연산량 측면에서 비효율적입니다. 이러한 문제를 해결하고자, 본 논문에서는 반복적인 local 연산 적용 대신, self-attention방식의 non-local 연산을 적용하여 long range dependence를 해결하였습니다.

논문에서 제안하는 non-local 연산의 이점은 다음과 같습니다.

1. local연산과 달리 두 위치간의 직접적인 연산을 수행하기 때문에 거리에 상관없이 모든 요소간의 관계를 파악
2. 적은 수의 레이어로도 best result 달성
3. 입력 변수의 크기를 유지하여 convolution과 같은 다른 연산과 함께 사용하기 좋음

논문에서 제안하는 Non-Local 연산은 영상 처리 기법 중 하나인 non-local means방식에서 영감을 받아 설계된 방법론으로 논문 방법론을 설명하기 앞서 non-local means filter의 개념을 살펴보고 넘어가겠습니다.

Non-Local Means

잡음이 포함된 이미지에서, 잡음을 제거하는 것을 image denoising이라 합니다. 이때 image denoising은 이미지에 여러 필터를 적용하는 것으로 진행되는데, 흔히 알고 있는 가우시안, 평균값 필터 등을 사용합니다.

Non-Local Means Filter는 노이즈 제거 필터의 하나로, 주로 speckle 형태의 랜덤 노이즈를 제거하는 데 사용됩니다.

랜덤 노이즈는 랜덤한 특성을 띄는 노이즈로, 영상을 촬영할 때마다 대상은 그대로 있지만, 조명 등의 요소에 의해 불규칙적으로 밝기가 다른 점이 발생하는 것을 의미합니다. 영상에서 랜덤 노이즈를 제거하기 위해 동일한 사진을 여러 장 촬영하고 촬영된 사진의 평균을 구하면 랜덤 노이즈를 제거한 영상을 구할 수 있습니다.

NLM Filter는 여러 장의 영상이 아닌 한 장의 영상만을 가지고 랜덤 노이즈를 제거하는 방법론입니다. [그림 2]를 보면, 한 장의 영상 안에 서로 유사한 영역들이 존재합니다. p 지점의 경우 q1, q2와 유사한 구조를 띄고 있어, 이러한 영역들을 모아 평균을 구한 것은 여러장의 영상을 평균해 준 것과와 유사한 결과를 얻을 수 있습니다. 이렇듯 전체 영상에서 일정 영역과 다른 영역간의 유사도를 구하고, 비슷한 영역끼리 평균 연산을 취하는 것을 Non-Local 연산이라 합니다.

Method

Non-Local Neural Nerworks

Non-Local Mean 연산은 영상의 전체를 탐색하여 영역 간의 유사도를 구한 후, 유사한 영역 끼리 평균 연산을 수행합니다. 이러한 non-local mean operation에 의해 논문의 generic non-local 연산은 [식(1)]과 같이 정의됩니다.

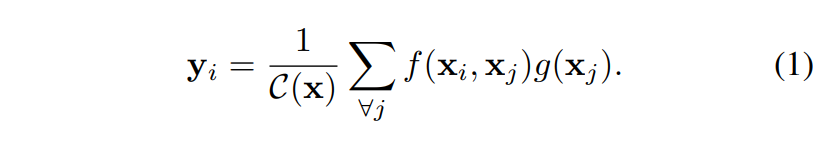
i는 출력 위치를 의미합니다. 이미지의 경우는 공간, 시계열 데이터의 경우에는 시간이 되겠죠. 그리고 j는 입력값에서 가능한 모든 위치의 인덱스를 나타냅니다. x는 이미지, 시계열, 비디오와 같은 입력 데이터 혹은 그 특징 벡터이고, y는 출력되는 특징 벡터입니다.

f는 x_i, x_y간의 simillarity를 계산하고, g는 입력 x에서 x_j의 a representation을 계산합니다. f(x_i, x_j)는 두 위치의 x_i, x_j의 similarity로, 논문에서는 두 입력 벡터의 채널축 dot product로 정의하였으며, 구체적인 정의는 [식(2)]와 같습니다.

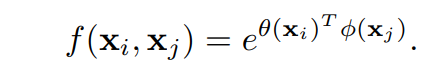
각 요소가 의미하는 바를 파악하고 [ 식 1 ]을 다시 보면, y를 계산하는 부분이 x 내에 존재하는 모든 위치(\forall j)와의 관계를 가중합하는 연산임을 알 수 있습니다.

Non-Local Block

위의 Non-Local operation을 다른 구조에도 쉽게 접목하기 위해서, 저자는 [ 식 ]과 같은 Non-Local block을 제안하였습니다.

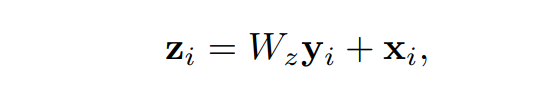
[ 식 3 ]에서 y는 앞서 [ 식 1 ]의 결과값이고, x는 residual connection을 의미합니다. residual connection에 의해 이미 학습된 모델 중간에도 non-local block을 끼워 넣을 수 있으며, 이러한 구조를 사용했을때 high-level, sub-sampled 특징 맵에서는 연산량의 향샹폭이 크지 않다고 합니다.

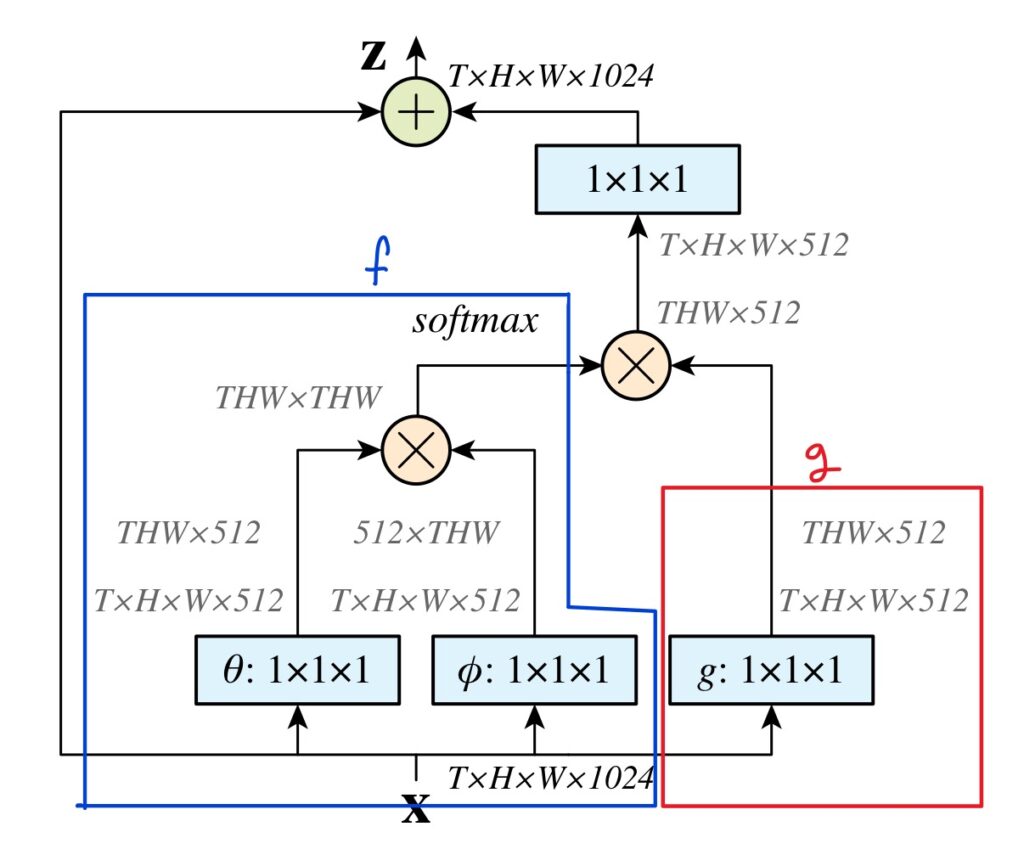
[ 그림 3 ]은 similarity function을 Embeded Gaussian으로 사용한 non-local block의 구조도입니다. 파란 색으로 표시된 부분이 f, 빨간 색으로 표시된 부분이 g이고, 1\times 1 \times 1이 작성된 블록들은 3D convolution입니다. [그림 3 ]에는 입력 벡터의 차원수가 4개로, 일반적인 이미지 데이터와 같이 H*W*C로 되어 있는 것이 아닌 T*H*W*C 형태로 되어 있는데, 이는 학습 데이터로 비디오를 사용하였기 때문입니다.

Experiments

논문에서는 Kinetics dataset이라는 데이터셋을 이용하여 실험을 진행하였습니다. Kinetics dataset은 비디오 데이터셋으로, 24.6만개의 training data, 약 2만개의 test data로 구성되어 있으며, 각 비디오는 한 가지 동작과 연관되어 있어, 비디오를 보고 사람의 동작을 맞추는 classification task를 수행하였습니다.

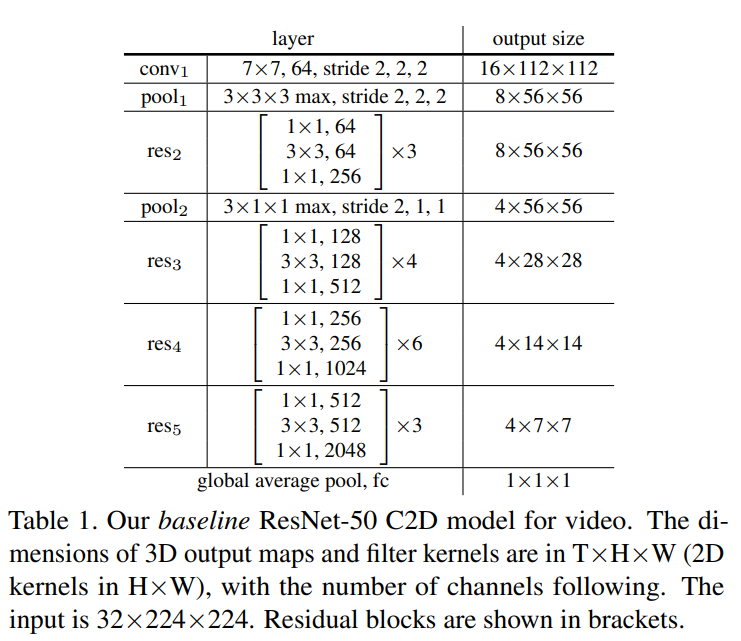
해당 실험에는 resnet-50을 베이스로하는 두 가지의 모델을 사용하였는데, 하나는 2D ConvNet baseline (C2D)모델로 우리가 흔히 알고 있는 ImageNet으로 pre-trained된 resnet모델에 [ 표 1 ]과 같이 time축을 포함하여 3*3*3, 3*1*1로 pooling을 수행하는 모델입니다.

다른 하나는 Inflated 3D ConvNet (I3D)모델로 C2D모델과 거의 동일하나 1*1, 3*3 convolution 대신 3*1*1, 3*3*3의 3D convolution을 사용하였습니다. 증가한 차원 만큼의 파라미터는 기존 C2D의 파라미터를 활용하였습니다.