안녕하세요. 네 번째 X-Review입니다. 해당 논문은 point cloud를 딥러닝 모델의 입력으로 하는 과정을 담은 첫 논문으로, 오픈 세미나에서 말씀드렸던 것과 같이 관심 주제인 object detection 중 3D object detection을 위한 3D 데이터 관련 논문을 읽어보고자 했습니다.. 이전 두 분의 연구원께서 이미 해당 논문에 대한 리뷰를 작성해주셨지만, 저는 근본적인 point cloud에 조금 더 중점을 맞추어 자세히 다뤄보겠습니다.

---

Point cloud

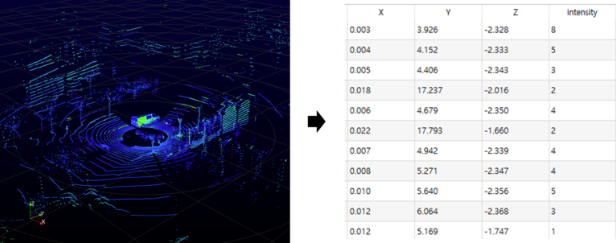
Point cloud는 3차원 상의 점의 집합입니다. 3차원 상의 점이라 한다면 2차원 이미지 데이터의 하나의 Pixel(x, y) 에서 depth 정보를 더한 (x, y, z)로 표현할 수 있을 것입니다. 그렇다면 3차원 상의 점을 수집하는 방법에 대해 궁금해집니다. 3차원 상의 점은 물체에 대해 Lidar 센서, RGB-D 센서 등의 센서로부터 빛이나 신호를 보내 돌아오는 시점을 빛, 시간의 속도를 활용하여 거리 정보를 계산하여 생성합니다. Point cloud는 3차원 공간 상의 점들의 집합을 의미하며, 아래의 그림과 같이 표현됩니다. Lidar 센서로 수집된 Point cloud를 보면, 백지에 연필로 하나의 점들을 찍어놓은 것과 같습니다.

그렇다면 3차원 상의 점은 2차원 상의 점과 어떻게 다를까요? 물론 깊이 정보인 z축을 포함하니, Nx3 의 행렬 형태로 표현되며 2D 이미지 데이터의 위치는 항상 양수로 표현되나 Point cloud의 위치는 양수 외에도 음수를 가질 수 있습니다. 외에도 이미지 데이터에서 좌표 값, 즉 데이터 값은 0-255 사이의 정수로 표현되나 Point cloud에서는 실수로 표현된다는 차이점등이 존재하지만, 이 밖에 굉장히 중요한 성질이 있습니다. 아래의 그림을 보겠습니다.

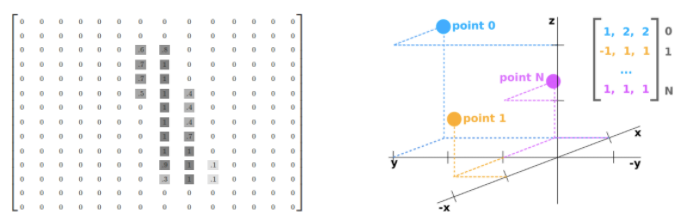
2D 이미지 데이터는 항상 좌상단의 지점을 기준으로 잡아, 각 픽셀의 위치 정보를 계산합니다. 하나의 지점을 기준으로 삼는다는 의미는 위치 정보를 내포할 수 있다고 볼 수 있습니다. 이 점이 굉장히 중요한데, 그 이유는 우측 그림의 Point cloud의 기준은 센서의 위치로, 3차원 행렬로 나타냈을 때 좌상단 지점을 기준으로 삼을 수 있는 근거가 없습니다. 바로 이러한 특성으로 데이터 특성이 regular인지, irregular인지를 파악할 수 있습니다. 특히 딥러닝 모델 기반 연구에서는 정형화된(regular) 데이터를 위주로 다뤘습니다. 물론 2D 이미지 데이터만이 아닌 3D voxel 등에 대해서도 다루고 있지만, 비정형화된 Point cloud 등에 대해서는 이전 연구들에서는 다루지 않고 있습니다. 그렇다면 우리가 Point cloud를 딥러닝 메돌 의 입력으로 적용한다면, 그 자체만으로 굉장한 Contribution이라 볼 수 있습니다. 그리고 그 논문이 오늘 소개할 PointNet입니다. 그렇다면 다시 돌아가, Point cloud 데이터는 어떠한 성질을 갖고 있으며, 해당 성질들이 왜 딥러닝 모델의 입력으로 넣는 것에 한계가 있었는지를 보겠습니다.

Permutation Equivariance

permutation invariance는 input 데이터들에 대해 그 순서에 상관 없이 동일한 output을 내뱉을 수 있는 성질입니다. 친숙한 예로 MLP를 보면, 입력 데이터의 순서와 상관없이 노드들의 연산을 통해 동일한 output을 뱉을 수 있습니다. 그렇다면 CNN은 그 자체로는 permutation invariance하다고 볼 수 있나요? 아닙니다. permutation invariance 하려면 입력 데이터의 순서, 즉 이미지를 예로 보면 이미지의 모든 픽셀을 무작위로 바꾸더라도 동일한 결과를 내뱉어야하는데, 쉽지 않습니다. 하지만 CNN에서 permutation invariance를 보장할 수 있는 하나의 성질이 있습니다. 바로 Max pooling인데, 이 점에 대해서는 permutation invariance를 수학적인 관점에서 보겠습니다. 순서에 따라 동일한 output을 내야하니, 다음의 수식처럼 표현할 수 있습니다.

f(x, y, z) = f(y, z, x) 수학적인 관점에서 이는 symmetric function, 즉 변수의 위치를 바꾸더라도 변하지 않는 다항 함수를 의미합니다. CNN의 Max pooling을 수학적으로 보면, 2×2 filter 내 x, y, z, w에 대해 f(x, y, z, w) = max(x, y, z, w) 입니다. 전체적으로 보면 Permutation equivariance하지만, 커널 내에서만보면 Permutation invariance 하다고 볼 수 있습니다. 바로 이 점이 중요한데, Point cloud는 입력 데이터의 순서가 없습니다. 정해진 MxN 사이즈의 격자 구조의 형태 안 정보가 저장되어 있는 2D 이미지 데이터와 달리, 3D 공간 상의 수 많은 점들을 Lidar 센서에서 신호를 받는 순서대로 기록하니, 점들 간의 상호 작용 및 관계를 파악하기 어렵습니다.

그렇기에 Permutation invariance를 보장하는 것은 중요하며, 해당 논문에서는 위에서 소개드린 Max pooling의 symmetric function을 사용합니다. 다시 말하자면, Point cloud의 n개의 점에 대해 생길 수 있는 경우의 수는 n!이며, 모든 경우에 대해 동일한 output을 뱉는 것이 중요합니다. 아래에서 모델의 구조를 보며 다시 설명하겠습니다. 다음은 Point cloud의 다른 성질에 대해 보겠습니다.

Sparse, Transformation Equivariance

2D 이미지는 정해진 격자 내 모든 pixel 값이 기록되어 있습니다. 그러므로 당연히 dense하다고 볼 수 있습니다. 하지만, Point cloud는 센서에서 보낸 신호가 다시 돌아올 때, 그 신호들을 기록하기 때문에 2D 이미지에 비해 빈 공간이 상당히 많습니다. 아래의 그림을 보면, 대략적인 물체의 형상을 알 수는 있지만 2D 이미지 데이터에 비해 빈 공간이 훨씬 많기 때문에, 이러한 성질로 인하여 Point Cloud 데이터를 다루는 3D 인공지능 모델은 한계를 보입니다. 또한 Point cloud 데이터를 다루는 3D 모델을 다양한 transformation에 invariance하기엔 어렵습니다.

위에서 언급한 것과 같이 점들 간의 상호 관계를 파악하기에 어렵기 때문이며, 데이터가 갖는 기하학적인 특성을 파악하기 어렵기 때문입니다. 위의 특성들로 인해 이전의 연구에서는 Point cloud를 voxel이나 collections of image로 변환하여 사용합니다. 하지만 이렇게 변환하는 방법 또한 문제점이 있으며, 이는 아래에서 살펴보겠습니다. Voxel에 대해서도 다루고 싶은데, 다음 VoxelNet을 리뷰할 때 다시 한번 자세히 살펴보겠습니다.

Abstract

위에서 설명한 Point cloud를 입력으로 하는 방법론입니다. 이전의 연구들은 Point cloud 데이터를 3D voxel grid나 collections of image로 렌더링하여 사용하는데, 해당 방법은 연산량과 메모리 측면에서 비효율적이며 데이터 본질의 표현력을 해친다고 말합니다. 의문점으로 Point cloud를 3D voxel 형식으로 나타내면 다운 샘플링 효과를 내어 연산량의 부하를 감소하는데, 왜 이렇게 표현했는지에 대해 생각해봤을 때, 다음의 두 결론이 나왔습니다.

데이터 자체로는 Voxelization이 연산량을 감소시키는 것 처럼 보일 수 있지만, 네트워크의 입력으로 사용하여 연산량을 비교해봤을 때 Point cloud 방법이 더 좋았거나, 혹은 point cloud를 2D 이미지의 집합으로 만드는 collections of image 과정은 분명 더 많은 연산량을 불러올 것이므로 이 부분에 대해 언급했을 수 있겠다 싶습니다. 다음으로 데이터 본질의 표현력을 해친다는 표현은 어떤 것일까요? Point cloud는 연속 공간인 continuous space에 있으나, 이를 voxelization하면 voxel grid filter를 거치며 중심점만이 샘플링되기 때문에 이산 공간인 discrete space에 있습니다. continuous space에서 discreter space로 이동했다는 것은 샘플링 시 발생할 수 있는 양자화 오차를 생각할 수 있으니, 그 부분에서 원본 데이터의 표현력을 잃을 수 있다고 볼 수 있습니다. 결국 Point cloud를 object classification이나 segmentation 태스크에 딥러닝 모델의 입력으로 직접 적용하는 것이 이전의 연구에 비해 효율적이며 좋은 성능을 보인다고 합니다. 이외에도 input perturbation, corruption과 같은 노이즈나 데이터의 변형에도 강인한 특성을 가진다고 하는데, 한번 살펴보겠습니다.

1. Introduction

Introduction에서의 이야기는 결국 Point cloud에 관한 이야기입니다. 이전의 방법들이 3D voxel과 같은 데이터 형태를 어떻게 사용하였는지, 해당 방법이 Weight sharing, kernel optimization 등을 사용한다고 하는데, 이는 다음 리뷰 예정인 VoxelNet에서 다룰 예정이니 다음 번에 보겠습니다. 결국 핵심은, 해당 데이터 포맷을 사용한 핵심적인 이유는 regular format 이기 때문입니다. regular format을 받는 형태는 DNN의 기초이자 Inductive bias라고 볼 수도 있겠네요. 결국 3차원의 기하학 정보를 갖는 Point clouds를 입력으로 하는 PointNet을 소개합니다.

이미 Point clouds의 특성에 대해서는 위에서 설명했지만, 본 논문에서 언급하는 점은 Point cloud는 단순히 점들의 집합이기 때문에, invariant to permutation, 즉 입력 데이터의 순서에 불변한 출력을 내야하며 translation, rotation 과 같은 rigid motion에도 불변한 특성을 고려해야합니다. PointNet은 Point clouds를 입력으로 받아 classification이나 segmentation의 task를 진행할 수 있으며, 네트워크의 각 레이어는 점들을 동일하거나 혹은 독립적으로 연산하여 처리합니다. Symmetric function인 max pooling을 사용하여 interesting or informative points, 특징이 되는 점들을 선별할 수 있습니다. max pooling을 통한 결과값들을 모아 FC layer를 통과시켜 global descriptor로 만들어 다양한 태스크를 진행합니다. 또한 해당 논문을 읽고자 한다면 STN, Spatial Transformer Network의 구조를 이해해야합니다. 이는 3차원의 각 점들이 독립적이기 때문에 rigid나 affine transformation을 적용하기에 용이하므로, STN 을 네트워크에 더하여 각 점들을 정규화하는 과정을 거칩니다. 이 부분에 대해 당장은 말로만 짚고 넘어간다면, 선이나 도형은 해당 선과 도형을 이루는 점들이 연관되어있기 때문에, 특정 변환을 거칠 때도 연관된 관계는 보존되어야 합니다. 이외에도 네트워크는 연속인 Point cloud의 set function을 근사할 수 있으며 (연속의 데이터를 다룰 수 있는, 다른 말로는 그냥 Point cloud를 사용할 수 있다는 말입니다) 위에서 말한 outliter와 missing data 들에 대해서도 강인하다는 말을 합니다.

결국 data perturbation과 corruption에 강인하다고 하는데, 네트워크의 구조를 살펴보고서 다시 설명드리겠습니다. 논문에서 말하는 Key contribution은 다음과 같습니다. 1. unordered 3D data format인 Point cloud를 다루기에 적합하게 모델을 디자인했다. 2. classification, segmentation에 모두 활용 가능하다. 3. 결국 Point cloud를 처음 다룬 논문이기에, 이론적이고 실험적으로 분석 결과를 내었다 (Analysis에서 확인할 수 있습니다.)

2 Related Work

Related Work는 Point Cloud Feature를 사용한 방법(이전의 방법들은 3D Voxel Grid로 렌더링하거나 혹은 2D 이미지로 만듭니다.)과 Unordered한 집합들에 대한 딥러닝 방법론들을 다룹니다. 일단은 네트워크 이름과 간단한 설명으로 넘어가며, 추후 팔로업하며 해당 논문에 대해 자세히 살펴보겠습니다.

먼저 기존의 Point cloud를 Feature로 만드는 방법 중 Volumetric CNNs은 voxelization을 통해 3D CNN을 적용한 방법입니다. 하지만 Sparse한 Point cloud를 Voxelization하게 되며 더욱 sparse해지므로 resolution에 제약을 받게되고 3D convolution의 computation cost도 많이 소요되어 비효율적이라고 말합니다. 그외의 FPNN과 Vote3D 모델은 Volumetric CNN의 sparsity한 문제를 해결하는 방법을 소개하나, 대량의 Point cloud set을 다루기엔 적합지 않습니다. Multiview CNN은 3D Point를 2D로 렌더링하여 2D Convolution을 사용하는데, 이는 shape classification이나 retrieval과 같은 태스크에는 적합하나 2D 이미지를 기반으로 하므로 3D 관련 태스크에 확장하기에는 물론 한계가 있습니다. 이외의 mesh를 활용한 Spectral CNN과 3D data를 vector로 변환한 Feature-based DNN 등이 있습니다.

다음은 Unordered Set에 관한 연구인데, 결국 이 부분에서 하고 싶은 말은 현재까지의 연구들이 regular input(speech, language processing, image, video 등)에 맞춰져 있기 때문에, 우리는 처음으로 Point cloud를 적용한다!라는 main contribution을 말하고 싶어합니다.

3 Problem Statement

센서에 따라 다르지만, Point cloud의 각 점들은 (x,y,z)의 좌표 정보 뿐만 아니라 색상 정보를 담은 feature channel 등을 가지고 있지만, 이번에는 (x, y, z) 좌표 정보의 점을 사용합니다. classification과 segmentation 태스크에서 point cloud를 어떻게 샘플링하는지에 대해서도 나와있지만, 가장 중요한 정보는 결국 (x, y)에 depth를 더한 (x, y, z)를 사용한다는 점이네요.

4 Deep Learning on Point Sets

4.1 Properties of Point Sets in \mathbb{R}^n

중요한 부분입니다. 이미 Point cloud에 대해 알아보며 Point cloud의 성질에 대해 알아봤지만, 딥러닝 모델에서 Point cloud를 다루기 위한 조건들을 짚고 넘어가겠습니다.

1. Unordered: N개의 3D Point에 대한 N! 경우에 대해 permutation invariance 해야 한다는 특징입니다. Point cloud의 점들이 어떤 순서로 입력되더라도, 물체의 3D 형태 자체가 달라진다고 볼 수 없기 때문입니다)
2. Interaction among points: 3차원 상의 점들은 Euclidean space 내에 있으며, 그러므로 점들은 기하학적인 의미의 연관성을 가집니다. 분명 위에서 Point cloud의 점들은 상관 관계가 뚜렷하지 않다고 말했지만, 위에서 말한 상관 관계는 Unordered한 특성으로 인해 근처의 두 점이 실제 3D 형태와 관련지어 연관되어 있다고 단언하기 어렵지만, Euclidean space 내 거리 정보만으로 보면 의미있다고 볼 수 있습니다. 그렇기에 이웃하는 점들과 local한 구조를 맺는데, 모델이 이러한 local 구조를 잘 잡아낼 수 있어야 합니다.
3. Invariance under transformations: rotatiion, translation 등의 transformation으로 인해 classification이나 segmentation의 결과가 변하면 안됩니다.

위의 모델의 조건을 상기하며, 구조를 보겠습니다. 아래는 PointNet Architecture입니다.

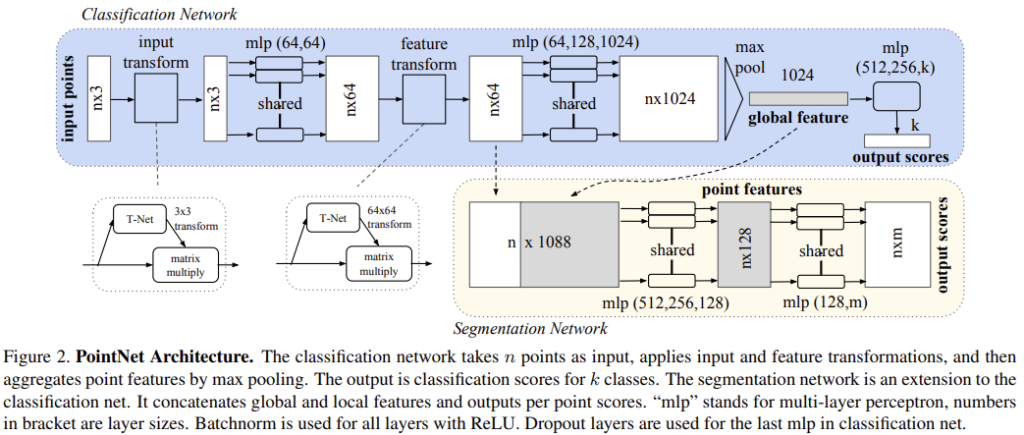
모델의 구조는 크게 1. max pooling layer(symmetric function) to aggregate information from all the points, 2. local and global information combination structure 3. two joint alignment networks that align both input points and point features의 세 부분으로 나눌 수 있습니다. 먼저 max pooling을 사용한 Symmetry function입니다.

Symmetry Function for Unordered Input

위에서 두 세번 언급했지만, 모델은 입력 순서에 불변해야하며(permutation invariance), 이를 위해서는 세 가지 방법이 존재합니다. 최종적으로는 symmetric function을 사용하지만, 나머지 두 방법에 대해서도 간단히 보겠습니다.

1. 입력 데이터를 표준 순서로 정렬합니다. canonicalorder이라고 하며, 고차원에서 perturbation에 안정적인 표준 정렬 방법이 없다고 합니다. 구글링을 해봤지만, 3D Point들의 canonical order에 대해서는 정확한 설명이 없으나, 뒤의 문장인 “그러한 order strategy가 존재한다면 고차원과 1차원 사이 전단사 대응이 가능할 것으로 보인다”는 것에서 입력 순서에 상관없이 순서를 대응시키는 어떠한 정렬 조건이라고 봐야할 것 같습니다. 혹시 아시는 분 있으시다면 댓글 부탁드립니다. 쨋든, 이러한 정렬 순서에 issue가 있으니, 입력에 대해 매번 정렬하는 것은 매우 힘든 일이라고 합니다.

2. 모든 permutation을 고려한 다음 RNN 방법을 사용하는 것이지만, 모든 permutation을 고려하여 augmentation 한다면 RNN의 permutation invariant를 보장할 수 있으나 그만큼 데이터 스케일이 커진다는 것인데, 이 상황에서의 RNN의 성능을 보장할 수 없다고 합니다. 실험파트에서도 보였다고 하니, 조금 있다 살펴보겠습니다. 결국, symmetric function을 사용하는 것이고, 여기서는 max pooling을 사용합니다. max pooling이 왜 symmetric function인지에 대해서는 위에서 설명했으니 넘어가겠습니다. 그래도 max pooling을 통해 global feature vector인 f가 나오는 과정은 꽤나 의미가 있으니, 수식으로 잠깐 살펴보겠습니다.

f(x_1, x_2, ..., x_n) = r \circ g(h(x_1), ... ,h(x_n)) , 수식 1

위의 그림과 결부시켜 이해해보겠습니다. 입력 Point cloud(수식 1의 x)에 여러 mlp (수식 1의 h)를 통과해 각각 n개의 점에서 1024개의 feature를 만든 다음, max pooling(수식 1의 g)을 통해 global feature vector(수식 1의 f)를 생성합니다. 그림에서 보면 결국 마지막 mlp을 통과해 k개의 classifcatioin output score를 뽑아내는 것을 알 수 있습니다.

Local and Global Information Aggregation

위의 Classification Network의 max pooling을 통과한 output vector는 f_1, ..., f_k 와 같이 표현할 수 있으며, 이는 Point cloud set의 global feature입니다. 해당 feature를 SVM, FC layer를 통과하여 classification 태스크를 수행할 수 있지만, segmentation은 global만이 아닌 local feature 또한 필요합니다. 이외에도 이웃한 점들과의 관계도 필요하기 때문에, 이들을 구하고 합칠 필요가 있습니다. 그렇기에 global feature vector와 max pooling 이전 단계에서 구현 point feature를 합친 feature vector를 Segmentation Network의 입력으로 사용합니다. max pooling 이전 단계의 feature transform을 거친 이후의 n \times 64 의 feature vector를 합쳐(1024를 n채널로 늘려 concatenate합니다) n \times 1088 의 shape을 가지며, mlp를 통과하여 nxm 형태의 output scores를 얻습니다. local feature vector와 global feature vector를 합치는 것으로 두 정보를 통합했다고 볼 수 있습니다. 결국 두 feature vector를 합친 다음 mlp를 통과하며 point 별 새로운 feature를 추출하는 것에 중점을 두고 보면 좋을 것 같습니다.

Joint Alignment Network

위에서부터 계속 언급한, transformation invariance를 위한 설계입니다. 새로운 네트워크를 설계한 것은 아니며, T-net (위에서 언급한 Spatial Transformer Network, STN을 의미합니다)을 통해 affine transformation matrix를 구하여 입력 point 별 transformation을 적용합니다. STN에 대한 설명은 이미 이승현 연구원님이 리뷰를 하셨으나, 다시 한번 간단히 짚고 넘어가보겠습니다. STN은 결국 transformation matrix를 찾아, grid generator로 transformation이 필요한 부분에 대해 transform 해줍니다.

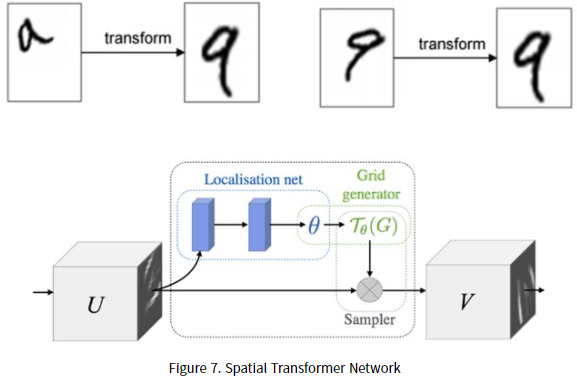
STN에 대한 자세한 설명은 지금 생략하지만, 꽤나 흥미로워 한번 읽어봐야겠네요. STN 네트워크의 motivation은 CNN이 translation, rotation, scale 변환 등의 transform에 약한 성질(spatially invariance)로 인하여, Input feature map U를 받아 Localisation net에서 transform matrix인 \theta 를 구한 다음, 해당 이미지가 있는 부분을 Grid로 만들어 변환을 진행합니다. 본 논문의 관점에서 보자면, input에 대해 rigid motion invariance를 만족시키고자 image를 수직으로 세웁니다. 이를 orthgonal하게 만든다고 표현하는데, 이 때 수직으로 세워진 공간을 우리는 canonicalspace라고 부르며 canonical space로 보내기 위한 transformation matrix를 input image 혹은 feature map에 곱하여 변형이 일어나지 않은, Point cloud의 point를 만들고자 합니다. 이 과정은 상단 Architecture의 T-Net으로 표현되어 있습니다. STN과 동일한 형태로 구성되어 있으며, 본 논문에서는 mini pointNet 혹은 T-net이라고 부릅니다. T-net은 point를 canonical space로 보내기 위해 적용되어야 하는 transformation matrix를 계산합니다. 그리고서 input에 transformation matrix를 곱하여, rigid motion invariance를 보장하며, pointNet에서는 input 뿐만 아니라 중간 feature map에서도 feature transform을 진행합니다. 이유는 mlp를 통과한 다른 feature point의 alignment를 맞추기 위함이며, 해당 feature transform을 통과한 feature vector를 local feature vector로 설정합니다. 단순히 transformation matrix를 계산하는 것이 아니라, 64×64 형태의 feature map의 transformation matrix를 predict해야하므로 optimization 시키기 어렵다는 단점이 있습니다. 당연히 계산상의 효율성과 transformation matrix의 매개변수를 생각하면 당연할 수 있는 부분입니다. 따라서 이 때 feature transformation matrix를 orthogonal matrix에 근사하기 위하여 정규화 식을 하나 추가합니다. 아래의 수식을 보겠습니다.

K_(reg) = (\parallel I - AA^T \parallel)^2_F 수식 2

수식이 복잡해보이지만, orthogonal matrix를 o라고 할 때, oo^T = I 임을 생각하면, 위의 수식이 곧 transformation matrix인 A가 orthogonal matrix가 되도록 근사하는 수식이라고 볼 수 있습니다. transformation matrix가 orthogonal matrix가 되면, input matrix에 transformation matrix를 곱해도 input의 rigid motion invariance를 보장할 수 있습니다. 즉, rigid motion에 대응되는 transformation matrix가 되도록 하기 위해 위의 정규화 수식 2를 추가하였습니다.

이제 Architecture에 대한 설명이 모두 끝났습니다. classification network만 따로 보고, max pooling의 이유에 집중해서 보고, T-net을 사용한 부분을 보고, local feature vector와 global feature vector를 합쳐 Segmentation network의 입력으로 한 부분을 보며, 각 MLP의 shape만 살펴보면 크게 어렵지 않을 것으로 보입니다.

5 Experiment

실험 파트는 다음의 네개로 구분됩니다. 1. 3D classificcation, segmentation 태스크의 성능을 보입니다. 2. Architecture 디자인 시의 Ablation study(?) 입니다. MLP를 사용했느냐, Max pooling을 사용했느냐, Average Pooling을 사용했느냐 등에 따른 성능을 보입니다. 3. 시각화 4. 시간 및 공간 효율성을 보입니다. 하나씩 살펴보겠습니다.

1. object classification

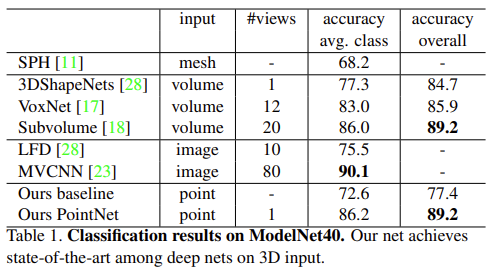
사용된 데이터셋으로는 ModelNet40 shape classification benchmark dataset입니다. 해당 데이터셋은 손수 제작한 12,311의 CAD model 이미지가 있으며, Related work에서 소개한대로 mesh, voxel, 그리고 3D 데이터를 다각도로 2D 렌더링한 image 방법과 비교했으며, 전반적인 성능이 가장 높음을 알 수 있습니다. 이때 point cloud를 사용한 방법의 baseline 모델은 단순히 point cloud에서 feature를 뽑아(어떻게 feature를 뽑는지는 해당 방법들을 봐야할 것 같습니다. point density, D2, shape contour 등등)에 mlp를 적용한 것이며, 전반적으로 성능이 낮은 것이 보입니다. 또한 inference 시간이 가장 짧았다고 합니다. 주목할만한 점으로는 MVCNN과는 성능 차이가 많지 않은데, 이에 대해 multiview image 렌더링이 point cloud가 갖는 sparse한 성질과 동시에 기하학적 정보가 많지 않음에서 기인했다고 보고 있습니다. 더 많은 point cloud가 더 높은 성능을 보일 것임을 말하는 것 같네요

2. 3D object part segmentation

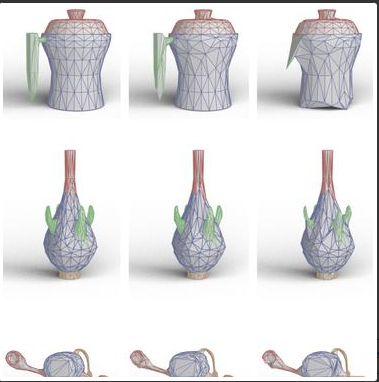
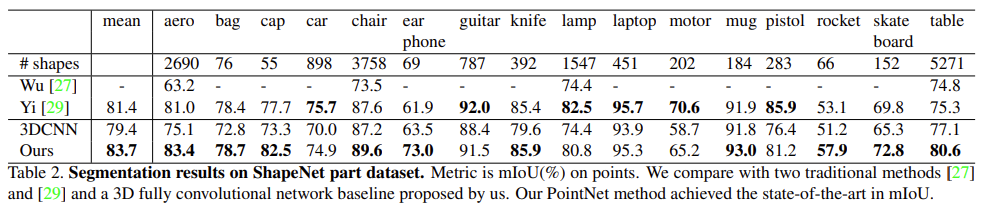
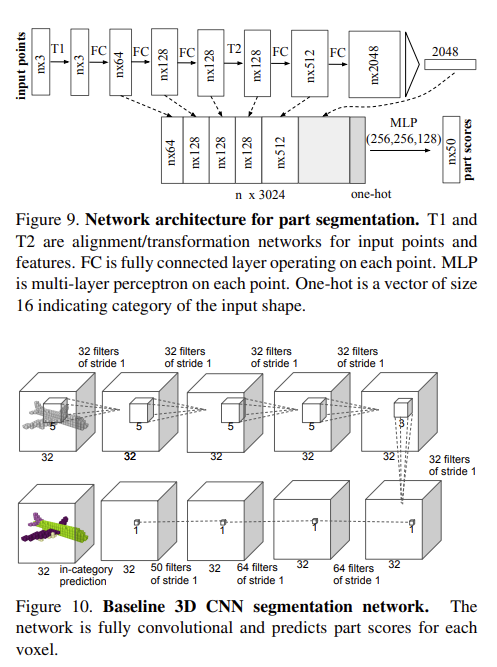
3D object part segmentation은 처음 들어보는 태스크인데, part segmentation이 3D recognition 태스크에서 세밀한 부분에 관한 segmentation을 진행한다고 합니다. 위의 사진을 예시로 가져왔는데, 저렇게 주전자의 손잡이 부분, 호리병 목부분에 대해 segmentation 하는 것과 같은 태스크인 것 같습니다. 사용한 데이터셋은 ShapeNet part dataset으로, 16,681의 shape와 16개의 카테고리, 그리고 전체 카테고리에 대해 50개의 part로 구성된 데이터 셋입니다. point 별 mIOU를 evaluation metrics로 할 때, 고전적인 방법론에 비해 좋은 성능을 보임을 알 수 있습니다. 해당 태스크에서 baseline으로 잡은 네트워크는 3DCNN으로, 3D convolution을 단순히 쌓은 모델입니다. Supplementary에서 part segmentation architecture와 3D CNN segmentation network를 확인할 수 있으며, 아래와 같습니다.

3. 3D object detection and Semantic Segmentation in Scenes

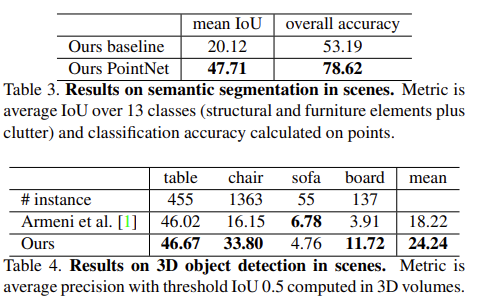
다음은 semantic segmentation 및 3D object detection에 관한 실험입니다. 사용한 데이터셋으로는 3D semantic parsing dataset을 사용했으며, 해당 데이터셋은 Matterport scanner로 3D 스캔 이미지(주로 방입니다)를 포함하고 있습니다. 해당 방에서는 의자, 식탁, 천장과 같은 object들이 있으며, 베이스라인으로 잡은 3D semantic segmentation 네트워크는 3D volumetric CNN이라고 합니다. 아직은 다양한 네트워크들에 대한 이해가 모두 되어있지는 않은 상황이라, 베이스라인 네트워크들에 대한 상세한 설명이 빠져 다소 아쉽습니다. 앞으로의 리뷰에서는 추가하도록 하겠습니다. semantic segmentation의 결과로부터 3D object detection도 진행했는데, 먼저 해당 과정에 대해서는 아래 Supplementary 자료를 보겠습니다.

segmentation score의 결과로 장면에서 object proposal을 진행했으며, BFS 알고리즘을 통해 근처 포인트를 탐색해나가며 같은 라벨을 붙인 다음 클러스터링 결과에 따라 하나의 오브젝트를 선정했습니다. 이 과정에 대해 조금 헷갈릴 수 있는데, 결과적으로 한 지점을 잡고! 0.2M를 반지름으로 하는 원을 그려서 근처에서 같은 segmentation 결과를 갖는 점들을 찾아 하나로 클러스터링하는데, 이 과정을 다른 segmentation 결과를 갖는 점을 만날 때 까지 반복한다고 보시면 됩니다(BFS 알고리즘에 대한 설명같네요). 그렇게 선정된 object에 대해 object detection을 수행하는데, 사실상 이 과정을 보면 단순한 알고리즘으로 object만을 보는 것이지, 정말 region proposal, bouding box 등의 결과로 object detection을 수행하지는 않네요. 다른 면에서, object detection 보다 더 좋은 성능의 semantic segmentation이 있다면? 이 방법을 조금 더 잘 튜닝하면 object detection의 한 방법론으로 자리잡을 수도 있지 않을까요? Hand-crafted 방법론 같지만, 방금 떠오른 아이디어여서 그냥 작성해봤습니다ㅎㅎ. small object 등에 대해서는 가지치기 한 후 성능을 봤으며, 높은 성능은 아니지만 그렇게도 가능하다. 정도로만 보면 될 것 같습니다.

5.2 Architecture Design Analysis

일종의 Ablation study?라고 보기엔 애매하지만.. 다양한 방법론을 적용했을 때의 성능 비교입니다. 먼저 Permutation invariance를 위한 방법들에 대한 성능 비교입니다.

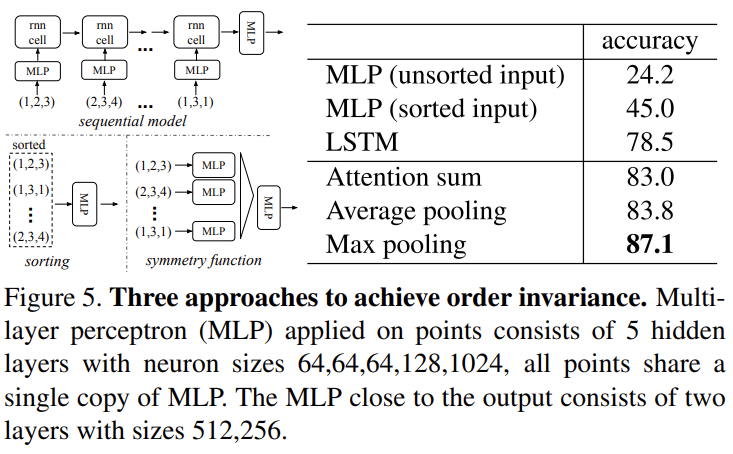
위에서 사용한 ModelNet40 shape classification를 기반으로 하며, unsorted input(무작정 인덱스 0번의 point부터 하나씩 대입하는 것과 같다고 볼 수 있습니다)과 sorted input(symmetric function인 max pooling을 사용한 방법입니다)에 대한 성능 비교를 보면, 당연히도 permutation invariance를 보장하는 sorted input MLP 방법의 성능이 훨씬 좋습니다. 지켜볼 점은 LSTM 모델의 성능인데, 물론 좋습니다. 당연히도 RNN은 symmetry function을 일종의 inductive bias로 하는 모델이며, 데이터 간의 연관성을 조금 더 잘 기억?할 수 있겠지만, 왜 RNN을 사용하기에 힘든지는, 위에서 언급했으니 넘어가겠습니다.

다음은 다양한 symmetry function 사이의 비교입니다. Attention sum, Average pooling, Max pooling이 사용되었으며 Max pooling의 성능이 가장 높음을 알 수 있습니다. attention method를 조금 살펴볼 필요가 있는데, 각각의 point feature로 부터 예측한 score를 softmax를 통해 normalize해주어 더해주는 연산인데, 해당 방법이 왜 permutation invariance를 보장하는지에 대한 자세한 설명은 없지만, 레퍼런스 논문을 후에 참고해보도록 하겠습니다. 저만의 이해로는, scalar score가 정확히 어떤 score인지는 모르겠지만, 근처에 있는 점은 비슷한 score를 가지므로 permutation 그 자체를 보장하여 입력으로 넣을 수 있기 때문이 아닌가. 생각하고 있습니다.

다음은 Input transformation과 Feature transformation에 대한 성능 비교입니다.

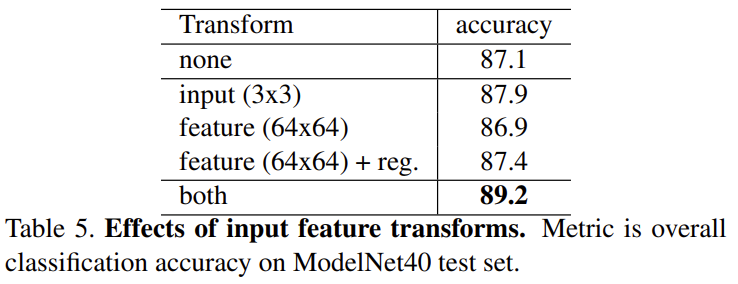
당연히 모델의 Architecture가 그랬듯이, 각 transformation을 적용해주는 것의 성능이 더 높습니다. 입력 point cloud 데이터들의 rigid motion invariance를 보장해주기 때문이라고 보는 것이 옳습니다.

그렇다면 이제 마지막으로, 시각화와 매개변수 및 FLOPs를 살펴보겠습니다.

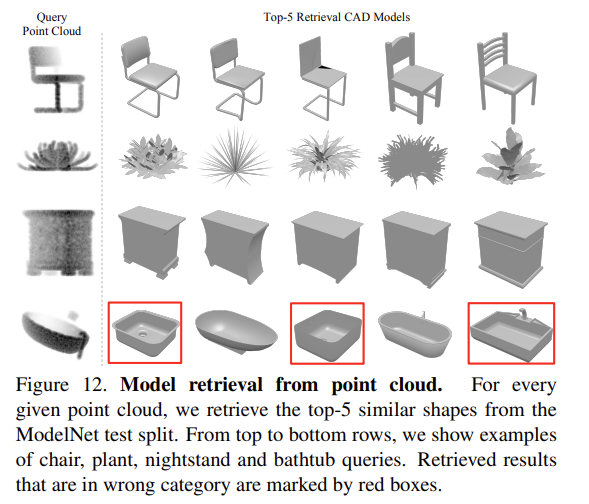
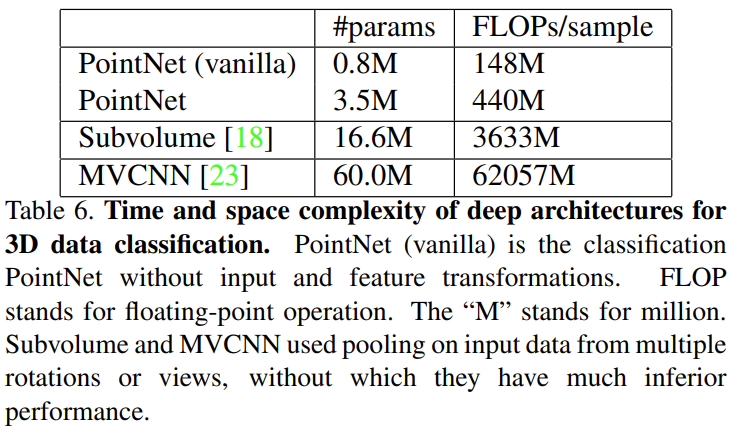
Supplementary에서 조금 재미있는 retrieval 결과를 가져왔습니다. Query Point Cloud에 대하여 ModelNet test 데이터셋으로부터 retrieval을 진행한 결과입니다. 정말 다양한 태스크에서 괜찮은 결과를 보이네요. 마지막으로 FLOPs를 보면, MVCNN은 위의 실험 결과에서 봤듯이 성능이 좋지만, FLOPs는 너무 많이 차이가 나네요..

Conclusion

결국, Point cloud를 3D object classification, segmentation 등의 태스크를 위한 네트워크의 직접적인 입력으로 넣을 수 있도록 모델을 디자인 한 것에 대해 언급합니다.

이번 리뷰를 작성하며, Point cloud의 기초부터 시작하여 다양한 태스크에 대해 어떤 태스크인지를 알기 위해 많은 공을 들였습니다. 3D object detection쪽 방법론이 Supplementary에 소개되어 있고, 그 방법이 조금 실망이였는데, 3D object를 어떻게 다룰 것인지, 다른 방법론들의 문제들을 함께 살펴보는 데에 굉장히 좋은 논문인 것 같습니다. 다양한 태스크에 대한 기초지식, 예를 들어 segmentation 태스크에 대한 기초 지식을 조금 더 쌓아야할 필요를 느낍니다. 아무쪼록, Supplementary까지 보며 봤지만 아직도 소개된 두 Theorem에 대해 이해를 못했는데, 시간을 내어 구글링을 더 해봐야할 것 같습니다. 이상으로 해당 리뷰를 읽어주셔서 감사합니다.