뜬금없이 Visual place recognition(VPR)을 읽어봤습니다. 읽을 필요는 없다고 하는데… 제가 지금 하려는 일이 물체 검색을 좀 원활하게 해보기 위해 프레임 레벨에서 패치(가칭)단위로 백그라운드를 suppression 할 수 있을 까에 대한 방향으로 고민을 해보고 있는데… 작업의 아이디어가 여기에서 왔는데, 안읽고 아이디어를 긁어와서 적용을 해보려니 너무 알송달송해서 그냥 읽어봤습니다.

Introduction

Patch-NetVLAD는 Visual place recognition에서 사용되는 방법론입니다. 이름에서 볼 수 있다시피, NetVLAD라는 기존의 방법론을 Patch단위로 적용한 방법론인데요. 이걸 알기 전에 이미지 descriptor에 대한 설명을 잠깐 듣고 넘어갑시다.

이미지에서는 쿼리와 레퍼런스 이미지를 표현하는 두가지 방식의 descriptor가 존재합니다. 쿼리 이미지와 레퍼런스 이미지간의 전반적인 유사도를 측정하는데 쓰이는 global descriptor와 특정 포인트와 포인트를 매칭하는데 쓰이는 local descriptor가 있습니다. Retrieval에서는 이런 경우 보통 Global descriptor로 Top-K 이미지를 고르고, Local descriptor로 Reranking하는데 VPR에서도 비슷하게 사용하는 것 같습니다.

이러한 두 descriptor가 각각의 장단점이 존재하기 때문에 이 둘을 융합하려는 연구가 있어왔고, 이 논문에서 제안하는 Patch-NetVLAD도 local과 global 정보를 상호 보완할 수 있는 방법입니다.

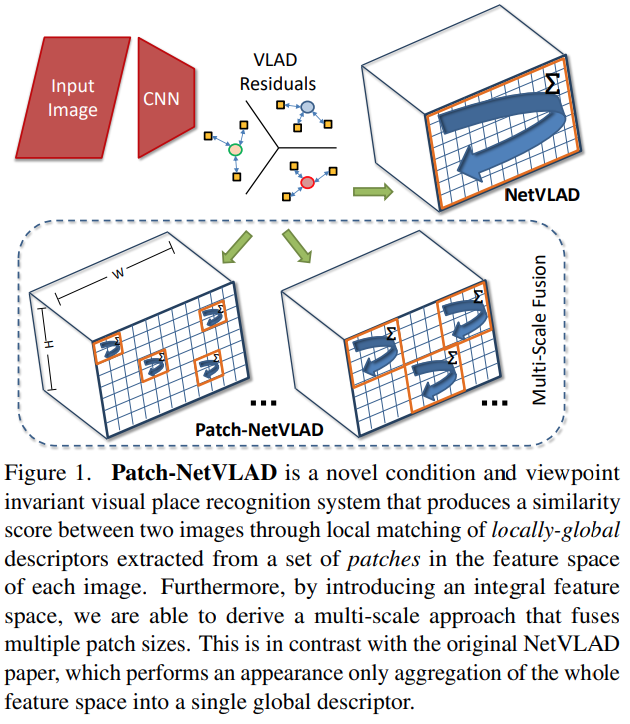
그래서 이 Patch-NetVLAD의 contribution을 정리해보면 다음과 같습니다.

• Locally-global descriptor의 매칭을 통한 얻어진 유사도를 바탕에 둔 VPR 모델
• 서로 다른 크기의 hybrid descriptor(서로 다른 크기를 가지는 Patch에서 추출된 feature)를 융합할 수 있는 multi-scale fusion 기술
• 성능도 좋은데, 속도도 빠른 SOTA

Methodology

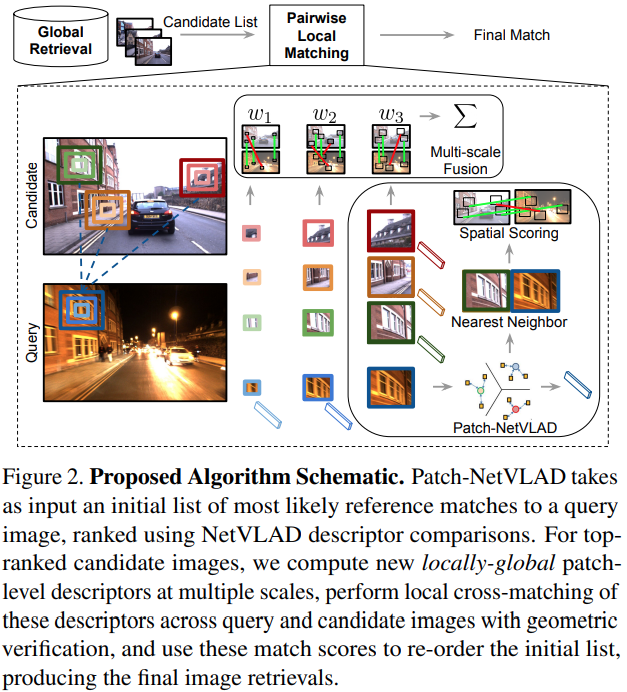
[그림 2]를 통해 이 모델이 어떻게 작동하는지를 파악할 수 있습니다. 일단 Global Retrieval이라고 되어있는 부분이 기존의 NetVLAD를 통해 수행되는데요. 이 부분이 이제 top-K(여기서 K는 100)개의 유사한 레퍼런스 이미지를 우선적으로 찾는 부분입니다. 이렇게 찾아진 K개의 이미지들에서 Matching 과정을 수행합니다. 이 매칭에서는 VLAD를 이용한 patch-level descriptors를 생성하고, 이를 통해 local matching을 수행합니다.

Original NetVLAD Architecture

그럼 NetVLAD가 어떻게 구성되는지를 알아봅시다. NetVLAD에서는 CNN 모델의 intermediate feature를 aggregate해서 사용하는 VLAD를 기본적으로 사용합니다.

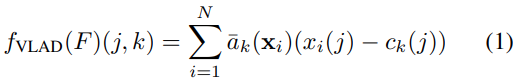
이 VLAD aggregation layer는 f_{VLAD}:R^{N*D} \rarr R^{K*D}로 정의되는데요. 이때 여기서 사용되는 VLAD 함수는 [수식 1]에서 확인할 수 있습니다.

• x_i(j) = i번째 descriptor의 j번째 element
• c_k = k번째 클러스터 중심
• \bar{a}_k = soft-assignment 함수

로 정의할 수 있는데요. 논문에서도 뭔가 애매하게 다루고 있어서 NetVLAD를 안읽고는 쉽게 설명할 수가 없네요. 그냥 특정 영역의 feature를 VLAD라는 모델을 통해서 embedding을 한 feature다 라고 생각하면 좋을 것 같습니다. 이렇게 나온 feature를 projection 시켜서 차원 축소를 시킵니다. f_{proj}: R^{K*D} \rarr R^{D_{proj}}와 같이 축소를 시키는데요. f_{proj}(f_{VLAD}(P_i))∈R^{D_{proj}}와 같은 projection 과정을 거쳐 차원 축소를 수행합니다. 이 뒤에 연산들은 VLAD 연산이니 넘어가고…

어쨋든 이러한 VLAD의 embedding 방식을 Patch-NetVLAD에서는 local patch에 적용했습니다. 기존의 NetVLAD 논문이 N=H*W라면, Patch-NetVLAD는 N< H*W로 가장 큰 차이점이 여기서 보입니다.

Patch-level Global Features

논문 이름에 Patch가 들어간 이유가 여기서 등장합니다. 여기서는 Patch라고 부르는 영역들에 대한 global feature를 추출하는데요.

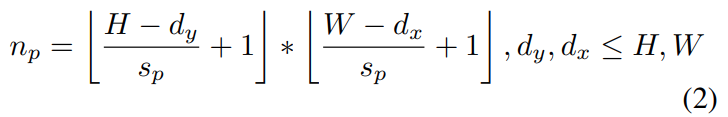
스트라이드가 s_p일 때, \{P_i, x_i, y_i\}^{n_p}_{i=1}로 정의되는 패치들을 뽑습니다. 이때 패치의 크기는 d_x, d_y로 표현되고 이 패치의 전체 갯수는 [수식 2]에 따라 결정된다고 합니다. (스트라이드 있는 CNN 커널 정도로 생각하면 될 것 같습니다.) 이렇게 추출된 패치를 바탕으로 이어지는 연산들을 수행합니다.

패치마다 앞서 설명한 대로, NetVLAD를 적용해서 feature를 추출합니다. 이 feature들은 f_i = f_{proj}(f_{VLAD}(P_i)) ∈ R^{D_{proj}}와 같이 얻어지는데, 잘 보시면 아시겠지만 “Original NetVLAD Architecture”에서 설명한 과정을 패치 단위로 적용한다는 차이만 있습니다.

Mutual Nearest Neighbours

패치단위로 추출한 feature 끼리의 유사도를 계산을 수행하는 방법에 대해서 다루는 부분입니다.

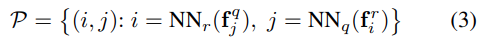
[수식 3]에서 확인할 수 있는데… q는 query, r은 reference인데… NN 함수는 Euclidean 거리의 최소값을 반환하는 함수입니다. 그래서 쿼리와 레퍼런스 사이의 가장 유사한 descriptor를 찾는 단순한 유사도 계산 부분입니다. 그냥 1대1 유사도 계산 매칭이지 특별한 부분은 없네요.

Spatial Scoring

유사도를 계산했으면 VPR이니 매칭이 중요합니다. 여기서는 spatial scoring을 위해 RANSAC 기반의 2가지 방법을 제안합니다. RANSAC 자체는 매칭 과정에서 outlier를 제거하기 위해 사용합니다.

RANSAC scoring

기본적인 RANSAC을 이용하는 방법 먼저 알아봅시다. 유사도를 계산할 때, inlier에 해당하는 패치들끼리만 계산하기 위해서 RANSAC을 사용해서 outlier를 제거하는 방식입니다. 여기서 패치를 2D 이미지 포인트라고 생각하면, 이미지 끼리의 homography를 구하는 걸로 대응시킬 수 있고, RANSAC을 사용할 수 있습니다.

Rapid Spatial Scoring

RANSAC과 같은 샘플링 과정을 빼서, 연산 시간을 줄이기 위한 방식인데요.

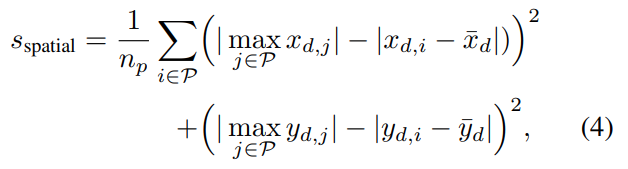
여기서 유사도는 [수식 4]와 같이 수행됩니다. 결국은 평균의 잔차의 합을 구한다고 하는 것 같은데… 우선적으로 x는 수평 방향이고, y는 수직 방향에서 패치끼리의 차이라고 가정합니다. 이때 x_d = \{x^r_i-x^q_j\}_{(i,j)∈P}이고, \bar{x}_d = {1\over{|x_d|}} \sum_{x_{d,i}∈x_d}x_{d,i}인데요. 잘 보면 앞은 레퍼런스 이미지와 쿼리 이미지의 패치의 유사도 차이가 되고, 뒤는 그 유사도 차이의 평균이 됩니다. 그래서 [수식 4]가 결국은 차이가 큰 패치(==아웃라이어가 되는 패치)에 영향력이 줄어들어서 RANSAC 없이 scoring이 가능하게 합니다.

Multiple Patch Sizes

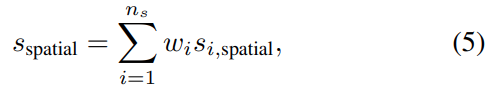
i번째 패치의 spatial score s_{i,spatial}과 w_i를 곱해서 서로다른 크기의 패치들의 score를 더해주는 방식을 통해서, 다양한 크기의 패치들을 앙상블한 scoring 방식으로의 확장도 가능합니다.

IntegralVLAD

본 논문에서는 패치단위의 연산을 중요하게 생각하는데, 이 patch descriptor를 여러가지 스케일로 원활하게 추출할 수 있는 IntegralVLAD를 제안합니다.

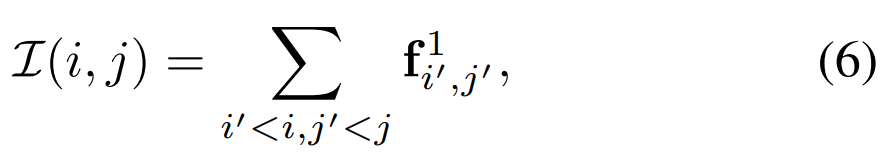
이 IntegralVLAD는 [수식 6]과 같이 정의되는데요. f^1_{i',j'}가 projection 전의 VLAD desciptor로 정의됩니다. 이때 feature가 1X1이기 때문에 i,j는 그냥 해당 위치의 feature를 가르킨다고 보면 됩니다.

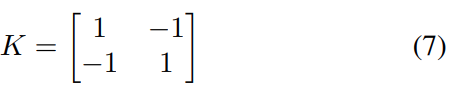
이렇게 integral feature map I를 생성했다면, 임의의 크기의 patch feature는 [수식 7]의 커널 K를 가진 2D depth-wise dilated convolutions을 통해 복구할 수 있는 형태로 손쉽게 얻을 수 있습니다.

Experiments

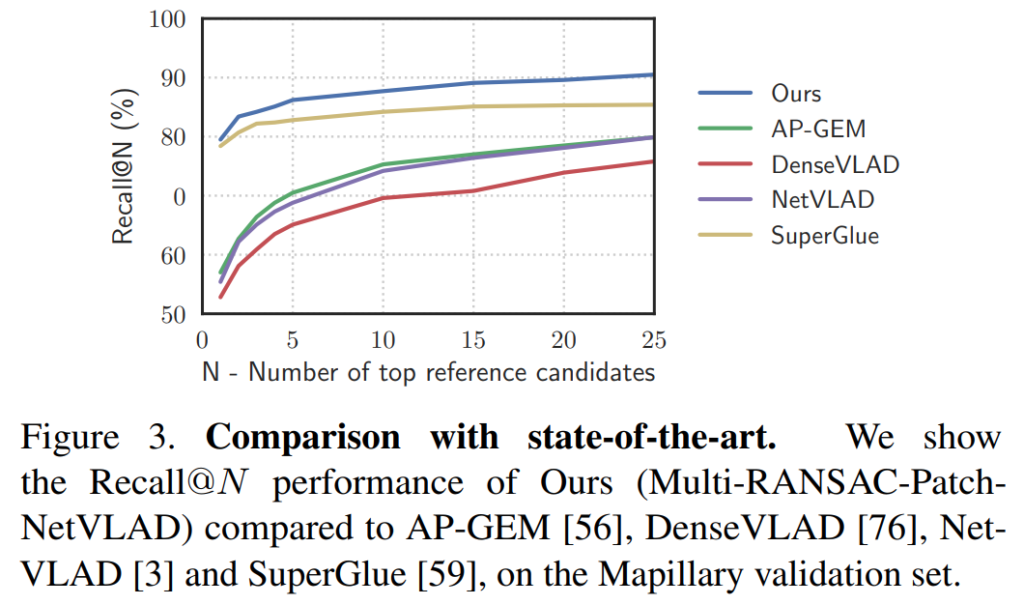
[표 1]과 [그림 3]은 SOTA 방법론들과의 비교입니다. 전반적인 성능이 높은 것은 맞는데, 일부 데이터셋(Pittsburgh, Tokyo)에서는 오히려 SuperGlue의 성능이 더 높습니다. 일단 이 부분에 대해서 unseen 환경을 마주했을 때 시각적인 차이가 클 때 성능 드랍이 많이 발생하는 특성 때문이라고 분석하고 있습니다. 이 문제는 데이터셋 차이로 발생하는 것 같은데 제가 아이디어 얻으려고 읽은거라 데이터셋은 잘 모르겠네요.

[표 2]는 ablation 표인데. 실험을 해볼만한 부분이 크게 두가지입니다. 패치 feature를 여러 크기로 쓰는지가 single/multi 표기이고, Spatial/RANSAC은 매칭에서 쓰는 차이입니다. 사실 뭐… 너무 당연하게 다 쓰는게 좋다는 결과가 나옵니다.

이거 말고도 속도 면에서도 SuperGlue 대비 월등히 빠른 부분을 확인할 수 있습니다.

정성적인 결과는 [그림 5]와 같은데 참고용으로 넣었습니다.

Conclusion

“locally-global feature descriptor”라는 포인트 때문에 읽은건데, 크게 도움이 되지는 않은 것 같습니다. 설명이 조금 부족한 것 같은데… 너무 쉽게 넘어가는 부분이 VPR 논문을 처음 읽는 사람에게 좀 어렵네요. 그리고 사실 “locally-global feature descriptor”에 대해서는 좀 내용이 없지않나… 결국은 NetVLAD인 것 같은 느낌입니다. 다른 논문을 좀 봐야 알겠네요.