오늘 리뷰하려는 논문은 2019년도로 다소 예전 논문인데요, 제가 궁금했던 부분에 대해 분석을 제시한 것 같아 읽어보았습니다. Active Learning에서 Uncertainty를 기반으로 데이터를 선별하기도 하는데요, 문득 Uncertainty가 정말 적합한 지표가 맞을까? 불확실성이 학습에서 보지 못한 새로운 데이터에도 동일한 경향을 보이나? 하는 의문을 분석한 논문이라고 생각되어 읽게되었습니다.
Why ReLU Networks Yield High-Confidence Predictions Far Away From the Training Data and How to Mitigate the Problem
- Paper: CVPR 2019 [ 바로가기 ], CVPR 2019 (accepted with an oral)
- Supplemental: [ 바로가기 ]
- Author Video: [ 바로가기 ]
- Code: [ Github ]
[1] Introduction
이 논문은 네트워크의 Over-Confidence 한 예측이 발생하는 이유를 분석한 논문입니다. Confidence는 다들 아시겠지만, 모델의 예측을 신뢰할 수 있는 정도라고 할 수 있을 것 같습니다. 그런데 저자가 의문을 가진 부분은 “학습 데이터와 전혀 다른 경향을 가진 멀리 떨어진 데이터임에도 불구하고 종종 ReLU Network가 과하게 높은 Confidence를 발생하는 것”이었습니다. 분명 신뢰도가 높으려면 학습 시 본 데이터거나 학습 데이터와 비슷한 경향을 보이는 데이터여야 합니다. 그리고 학습 데이터로부터 동 떨어진 데이터에 대해 모델의 예측이 높은 신뢰성을 보여선 안됩니다. 특히 안전과 연관된 Autonomous driving 혹은 medical diagnosis system과 같은 곳에서는 다른 도메인의 입력을 사용한다거나, 인간의 결정을 요청하는 등 출력에 대한 더블체크가 필요합니다.
그러나 문제는 이런 Far Away From the Training Data 에도 모델이 예측에 대해 high confidence을 발생하는 경우가 많이 리포팅되고 있다는 것이죠. 따라서 저자는 이 원인을 밝히고, 해결책을 제시하기 위한 분석을 제시하였습니다.
여기서 ReLU Network란 활성화함수로 ReLU 혹은 leaky ReLU가 사용되는 FC, Convolutiona, Residual 그리고 max/avg Pooling으로 구성되는 기본적인 네트워크를 의미합니다. 활성화 함수로 ReLU와 leaky ReLU로 제한하는 이유가 바로 piecewise affine classifier function에 제한한 분석을 제시하였기 때문입니다.
piecewise affine function 이란, 아래 그림과 같이 일정 구간 에 따라 정의된 함수라고 이해하시면 좋을 것 같습니다. (참고로 piecewise affine 은 piecewise linear라고도 합니다. 정확한 수식적 정의는 다음 챕터에 추가해두겠습니다.)

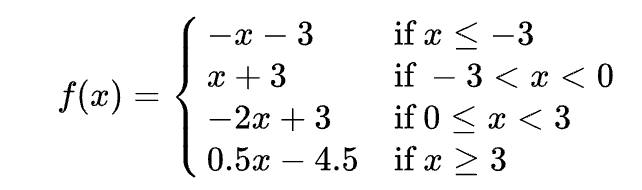
예를 들자면, 위에있는 수식이 바로 4조각으로 구성된 piecewise affine function 입니다. 따라서 ReLU 역시 f(x) = 0 (x<0), f(x) = x (x \geq 0) 로 정의된 piecewise affine function 이 되겠죠.
따라서 저자는 이렇게 piecewise affine function으로 구성된 모든 신경망이 Far Away From the Training Data에 대해 임의의 high confidence를 발생시킨다는 것을 보이며, 그 이유에 대해 분석하였습니다.
[2] ReLU networks produce piecewise affine functions
앞서 설명하였듯, 저자가 분석하는 네트워크는 piecewise affine function로 구성된 ReLU 네트워크 입니다. 따라서 이번 섹션에서는 ReLU 네트워크가 continuous piecewise affine function로 이어진다는 것을 보입니다. (참고로 이 증명들이 저자의 주장에 대한 주요한 근거가 되기도 합니다)

바로 앞에서 설명했던 정의 2.1.은 piecewise affine에 대한 정의입니다. 즉, 함수 f가 모든 Q_r로 제한될 때, 유한한 polytopes 집합 {Q_r}^M_(r=1)이 존재할 경우 piecewise affine 이라고 합니다. 우리가 비선형 함수에 대해 엄청나게 조밀한 영역에 대해 선형적으로 쪼개서 계산하는 것으로 이해하면 될 것 같습니다.
이렇게 piecewise affine activation function을 사용하는 네트워크는 continuous piecewise affine function으로 재작성할 수 있습니다. convolution, FC, residual, skip connection 모두 linear mapping이기 때문이죠. 따라서 정확히 말하자면, K개의 클래스로 분류하는 네트워크는 다음과 같이 나타낼 수 있으며 f: \mathbb{R}^d -> \mathbb{R}^K, 이를 조각 별로 나눈 각 component는 f_i: \mathbb{R}^d -> \mathbb{R} continuous piecewise affine function 가 됩니다. (이 때, (f_i)^K_(i=1)는 동일한 선형 영역 집합을 가집니다)
이제 ReLU 네트워크에 대한 각 레이어에 대한 수식을 정리하면 아래 수식과 같습니다. 아마 다들 익숙하실 겁니다. 참고로 \sigma(t) = max(0, t)는 ReLU 입니다.
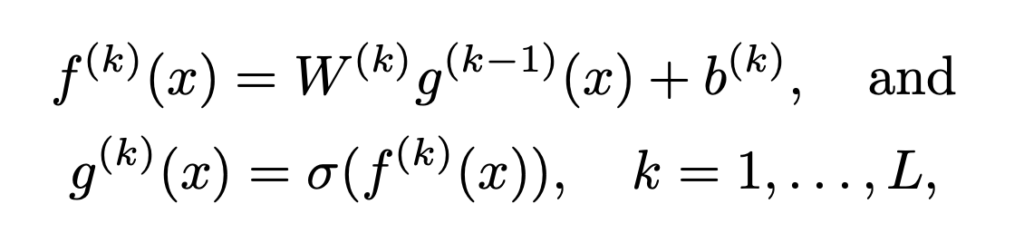
따라서 해당 네트워크의 최종 출력은 ![]() 이 됩니다. (L은 당연히 Layer 개수가 되겠죠)
이 됩니다. (L은 당연히 Layer 개수가 되겠죠)
그리고 ![]() 을 아래와 같은 diagonal matrix라고 정의하면,
을 아래와 같은 diagonal matrix라고 정의하면,
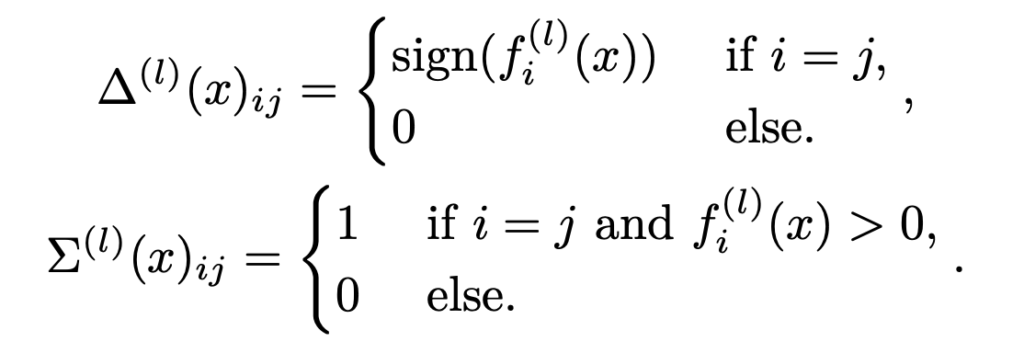
f^(k)(x)는 affine function으로 구성된 함수로 작성할 수 있게 됩니다.
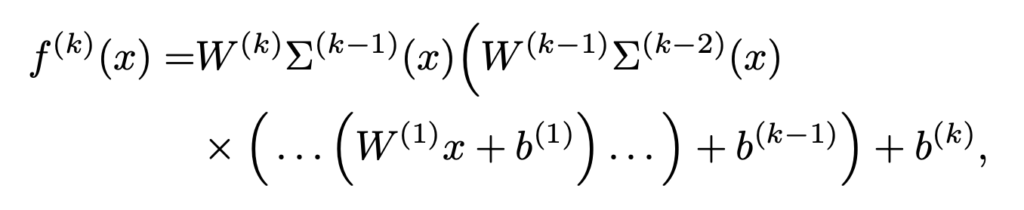
그리고 수식의 간단화를 위해 아래 수식을 사용하면,
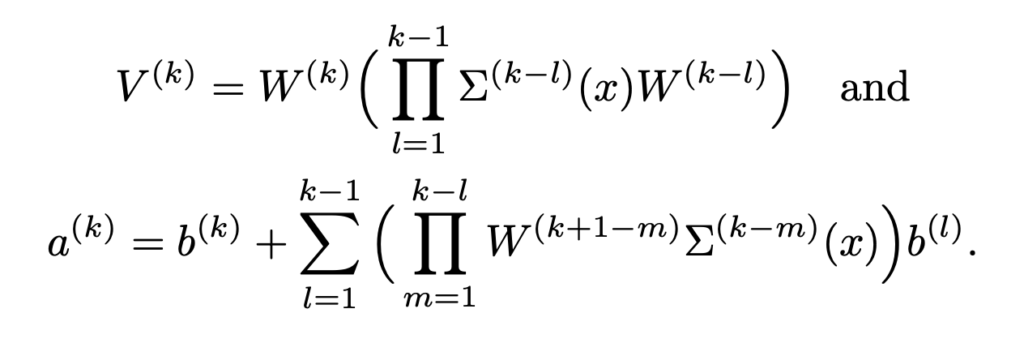
![]()
![]() 로 간단하게 표현할 수 있습니다.
로 간단하게 표현할 수 있습니다.
이제 마지막으로 x를 포함하는 선형 영역인 Polytope Q(x)는 ![]() 절반 공간의 교차점으로 특징지을 수 있고 다음과 같이 정의됩니다.
절반 공간의 교차점으로 특징지을 수 있고 다음과 같이 정의됩니다.
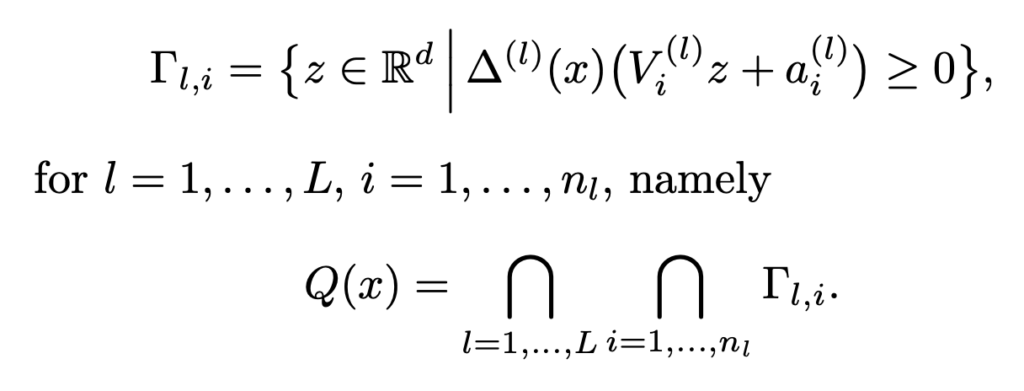
여기서 N은 hidden layer의 수를 의미합니다. 따라서 이제 ReLU 네트워크를 continuous piecewise affine function으로 재정의한 수식은 아래와 같습니다. 해당 수식은 Q(x)에 대한 affine 제한이 있습니다.
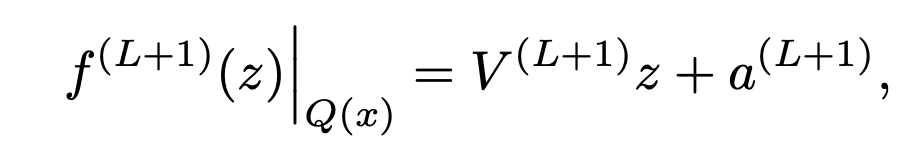
수식이 많아서 어려워보이겠지만, 차근차근 따라가면 다 따라가실 수 있을 거라 생각합니다.
[3] Why ReLU networks produce high confidence predictions far away from the training data
이제 저자가 밝히고자 한 far away from the training data에서 over-confidence prediction이 발생하는 이유에 대해 밝히는 챕터입니다.
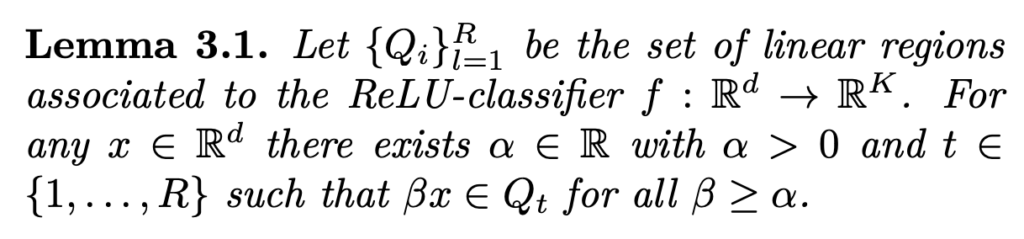
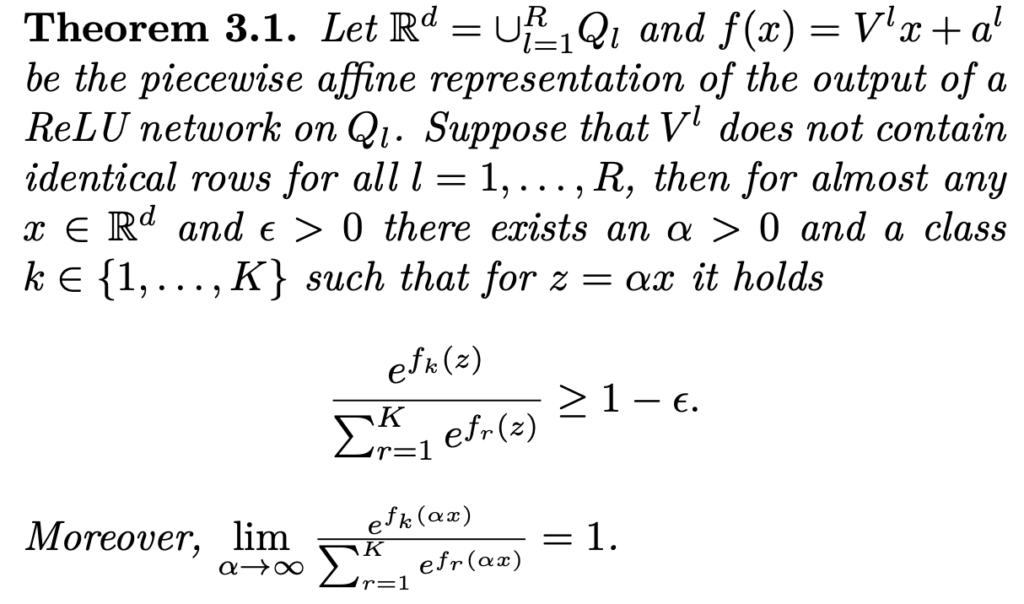
즉, 네트워크의 출력이 일정하지 않으면 정상적으로 학습된 네트워크라고 할지라도 unseen data에 대해 높은 confidence를 가지는 예측을 출력할 수 있다는 것입니다.
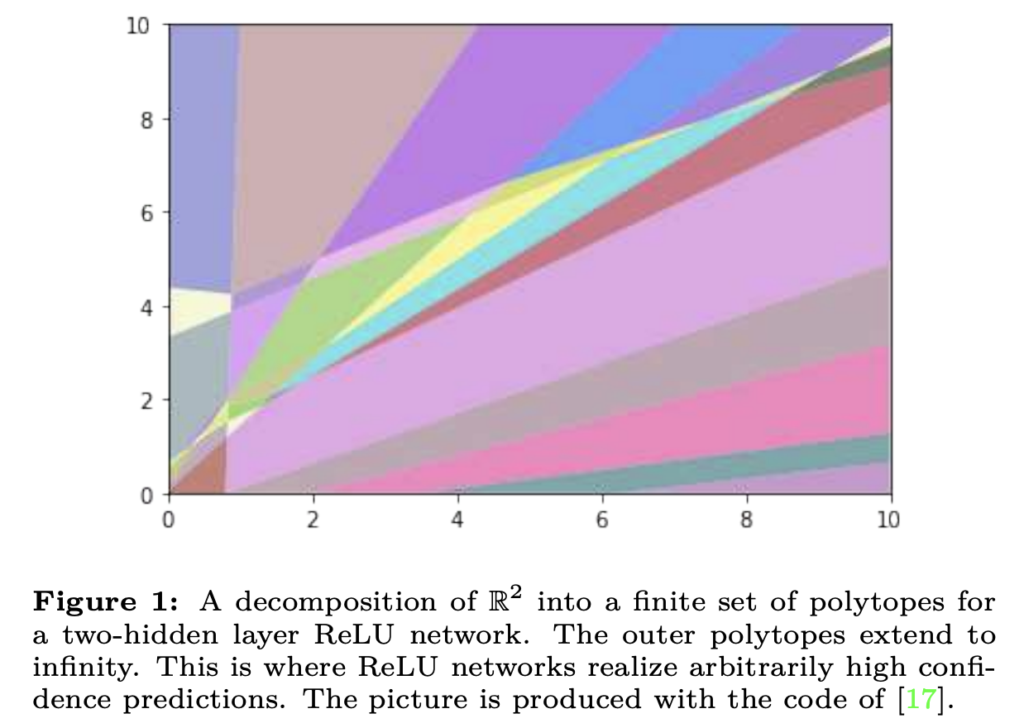
그 결과 ReLU 네트워크의 경우, 네트워크의 높은 Confidence 예츠을 임의로 실현하는 입력이 무한히 많다는 것을 의미한다고 합니다. 특히 기존에 over-confidence를 극복하기 위해 제안된 소프트맥스 보정 등으로는 이렇게 confidence가 높은 입력을 감지할 수 없다는 것을 알 수 있었다고 합니다. 이런 결과는 ReLU 네트워크의 구조를 수정하지 않고는 이러한 현상을 방지할 수 없다는 결론에 이를 수 있다고 합니다.
ReLU 네트워크와 반대로 RBF(Radial Basis Function) 네트워크는 학습 데이터에서 멀리 떨어진 곳에서도 거의 균일한 confidence prediction을 생성할 수 있는 특성을 가지고 있는 것으로 확인됩니다. 여기서 “멀다” 라는 것을 어떻게 정의되는지는 다음과 같이 정량화 할 수 있습니다.
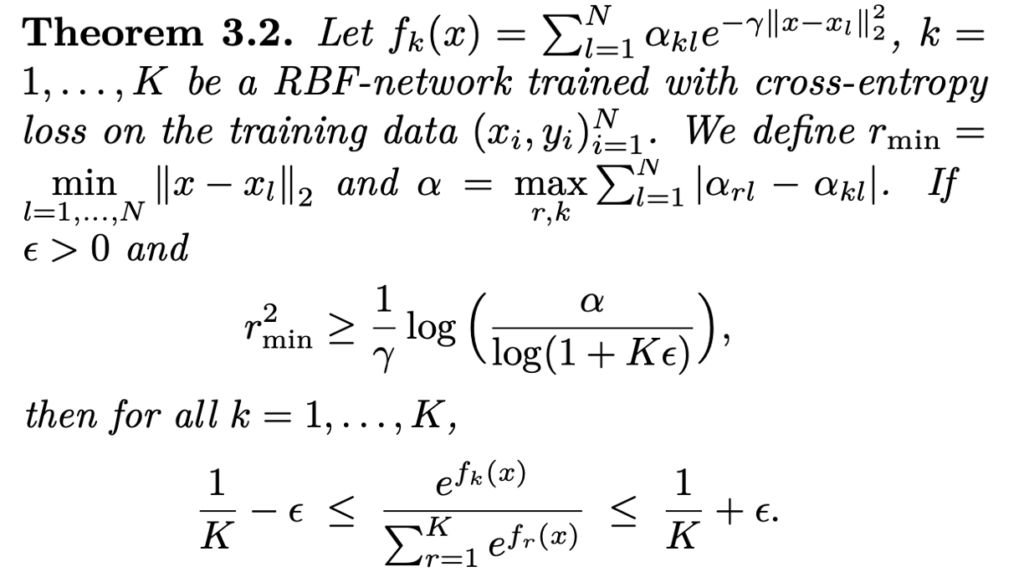
따라서 저자는 신경망 클래스에서 정리 3.2에서와 유사한 결과를 보이는 것이 매우 중요한 문제라고 합니다. 가령, \mathbb{R}^d와 같이 모데인이 제안되지 않은 경우에만 ReLU 네트워크에 대한 임의의 높은 신뢰도 예측을 얻을 수 있다고 합니다.
Experiment
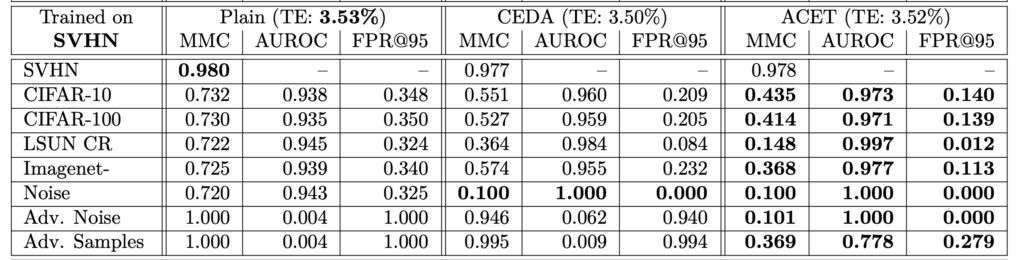
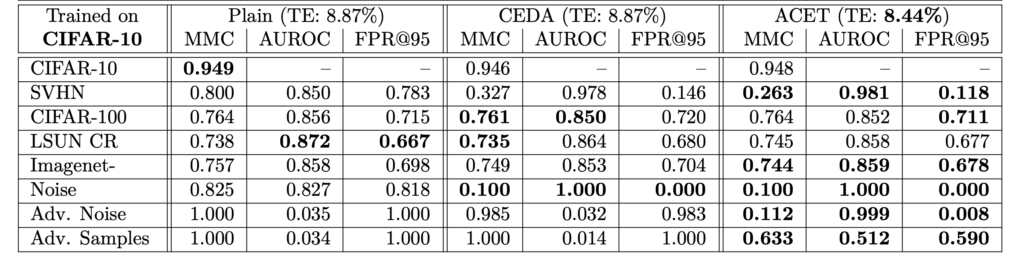
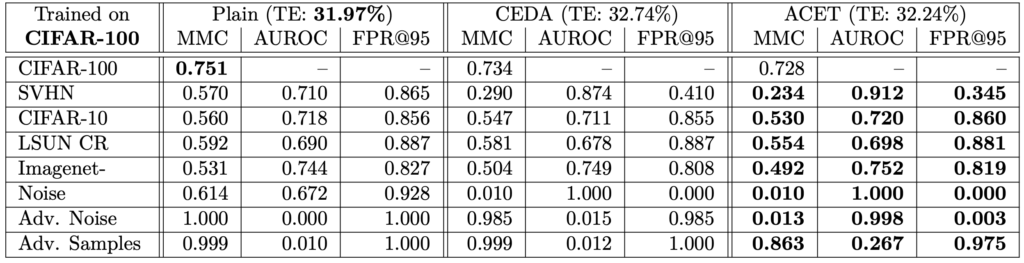
한 데이터셋에 대해 학습하고 분포가 다른 데이터셋과 노이즈 이미지에 대한 Confidence를 평가하여 실험을 진행하였습니다. MNIST, SVHN, CIFAR-10 그리고 CIFAR-100에서 학습하고, ResNet을 백본으로 사용하였다고 합니다.
아래 테이블을은 각각의 데이터로 학습한 결과를 나타냅니다. 우선, 세 가지 방법 모두 테스트 오류 사이 차이가 없다는 것을 확인할 수 있었습니다. 또한 학습 데이터에서 멀리 떨어진 곳에서 신뢰도를 향상시키는 것은 일반화 성능을 낮추지 않으며, Plain 모델은 항상 노이즈 이미지에 대해 높은 신뢰도 예측을 생성하고, Adversarial 노이즈에 대해 완전히 성능이 저하되는 것ㅇ르 알 수 있었습니다.
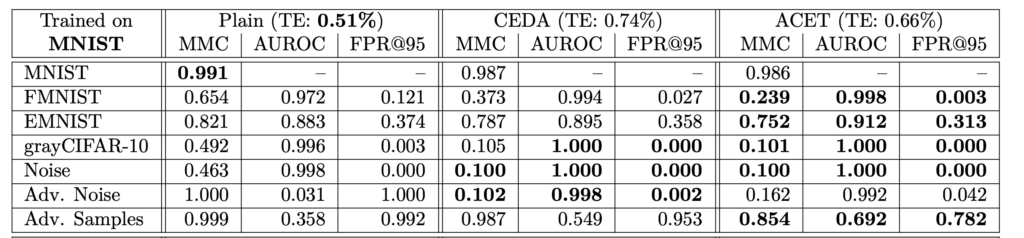
Conclusion
본 논문은 학습 데이터와 멀리 떨어진 ReLU 네트워크의 임의의 높은 신뢰도 예측 문제는 기존 보정법으로도 해결할 수 없다는 것을 보였습니다. 이건 신경망 구조가 가지는 고유의 문제임을 입증하여, 구조를 변경해야만 해결할 수 있음을 제시하였습니다.
![[CVPR 2019] Why ReLU Networks Yield High-Confidence Predictions Far Away From the Training Data and How to Mitigate the Problem](http://server.rcv.sejong.ac.kr:8080/wp-content/uploads/2022/12/image-119-675x554.png)
안녕하세요
해당 논문은 렐루 함수가 학습 데이터로부터 멀리 떨어진 경우에도 높은 컨피던스 스코어를 가진다는 것이 가장 큰 문제 정의 및 주요 쟁점이라고 생각하는데 리뷰에는 이에 대하여 다루는 내용이 그리 많지 않아보입니다.
네트워크의 출력이 일정하지 않으면 왜 하이 컨피던스 스코어를 가지게 되는 것인가요? 논문에서 캡처해주신 정리 3.2 내용만으로는 이해가 어려워서 주영님이 리뷰 내에서 추가로 설명해주면 좋겠습니다.
그리고 그림1은 무엇을 보여주기 위한 실험인가요? 해당 그림을 어떤 식으로 해석해야하는지 잘 모르겠습니다.
그리고 결과적으로 이 논문은 렐루가 하이 컨피던스 스코어를 가진다 라는 것에 대해 수학적 증명만 할 뿐 이를 해결하기 위한 새로운 기법을 따로 제안하지는 않는 것인가요? 그렇다면 이 논문이 cvpr2019에 붙게된 이유에 대해 주영님은 이 논문의 가장 큰 기여가 무엇이라고 생각하시나요?
일단 본 논문이 CVPR2019에 붙은 이유는 training 데이터와 ㄱ전혀 다른 경향성을 가지는 데이터임에도 불구하고 높은 신뢰성을 가지는 이유를 보였기 때문에 분석 면에 있어 큰 의미가 있따고 생각합니다. 다만 다시 읽어보니 이 부분에 대한 내용이 빈약한 것 같네요. 조금 더 자세하게 추가해보도록 하겠습니다. 또한 저자는 이를 극복하기 위한 새로운 네트워크를 제안하였는데 그게 바로 RBF(Radial Basis Function) 를 사용한 네트워크 입니다.
안녕하세요 좋은리뷰 감사합니다.
polytopes 이 의미하는 바를 이해하지 못하여 질문남깁니다.
학습 태스크의 종류를 의미하는 것이 맞나요?
polytopes란 직역하면 다포체로 다각형이나 다면체 등의 도형을 임의의 차원으로 확장한 것을 의미합니다
상당히 흥미로워 보이는 논문입니다. 리뷰 감사합니다.
이제 마지막으로 x를 포함하는 선형 영역인 Polytope Q(x)는 절반 공간의 교차점으로 특징지을 수 있고 다음과 같이 정의됩니다.
=> 이전까지는 수식의 흐름을 따라 갔는데 절반 공간이라는 게 무슨 말인가요?
또한 ReLU 다음으로 요즘 잘나가는 GeLU에 대해서는 별다른 분석이나 실험 내용이 없을까요?