Open Question:
How to select a training data subset that can theoretically and practically performs on par with the full dataset.
어떻게 일부 데이터셋으로 전체데이터셋을 학습한것과 같은 효과를 얻을까?
Countermeasure:
CRAIG. A method to select a weighted subset (or coreset) of training data that closely estimates the full gradient by maximizing a sub modular function. We prove that applying IG to this subset is guaranteed to converge to the (near)optimal solution with the same convergence rate as that of IG for convex optimization.
논문에서 제안하는 CRAIG는 학습데이터에서 가중된 서브셋을 선별하는 방법론으로 sub modular function을 최대화하여 전체 데이터를 이용한 full gradient를 가장 유사하게 추정하는 서브셋을 선별할 수 있는 방법론이다. 이 방법론을 이용하면 학습 데이터에 비해 데이터셋의 갯수가 줄어 빠르게 학습할 뿐만 아니라 convex optimization과 유사한 수렴을 보장할 수 있다.
Intro
앞서 open question 을 해결하기 위한 countermeasure로 CRAIG를 제안한 본 논문은 좋은 subset을 선별하여 학습을 효율적으로 진행하고자 했다. 결론적으로 제안하는 방식으로 선별한 subset을 이용했을 때 IG(Incremental Gradient)방법의 학습 속도를 로지스틱 회귀의 경우 최대 6배, 심층 신경망 훈련의 경우 최대 3배 향상시킨다는 것을 보여줍니다. 이때 IG란 SGD와 같은 optimizer다.
method
먼저 전체 데이터를 통한 gradient를 가장 잘 근사하는 서브셋을 선정하기 위한 목적함수 L을 정의해야한다. 이후 함수 L이 submodular 함수 F라 하면, S는 greedy 알고리즘을 통해 찾을 수 있다. 이러한 CRAIG는 실제 최적화 단계 이전의 preprocessing 과정으로 사용될 수 있다.
Incremental gradient(IG)는 일반적으로 전체 데이터셋 V에 대한 전체 그레디언트를 예측하고자 한다. CRAIG는 만약 그레디언트의 가중합이 V에 대한 가중합과 유사한 서브셋 S를 찾는다면, S에 IG 방법론을 적용하므로써 빠르게 수렴할 수 있는 솔루션을 찾을 수 있다는 것이다. 즉 서브셋S의 아이디어를 수식으로 정리하면 [수식1]과 같다
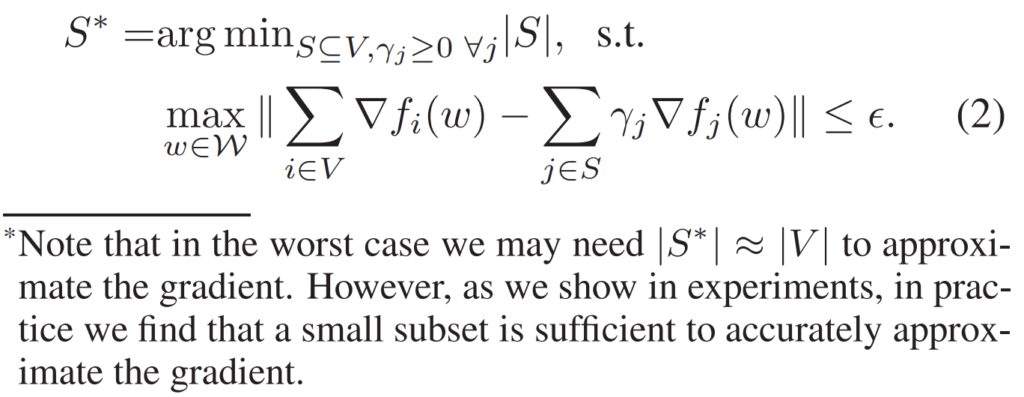
그러나 [수식1]을 바로 모델링하기엔 두가지 문제가 있다. 1) 위 식은 전체 모델 파라미터인 W에 대해 함수f의 그래디언트를 계산해야하며 이는 많은 연산량을 요구한다. (즉, 기존 V에대한 최적화와 연산량 비교시 효율적이지 않다) 2) 연산량을 감안해 위의 수식을 풀더라도 S를 찾는것은 NP-hard 문제이다. 즉, 완벽한 해로써 S는 찾을 수 없다. 그렇다면 near-optimal 된 서브셋 S를 찾는 방법은 무엇일까?
near-optimal S 찾기1:
S와 V가 같을 때 [수식2]는 성립한다.
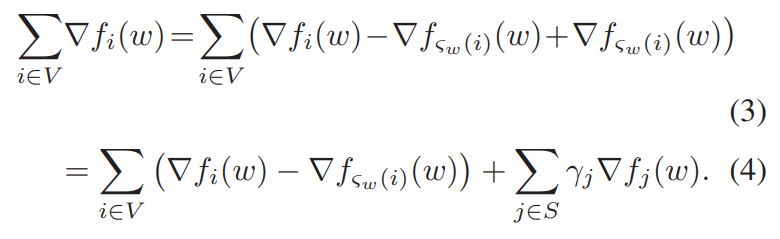
그러나 일반적인 상황에서 [수식3]이 성립한다. 등호가 성립할 때는, S와 V가 같을 때 이다.
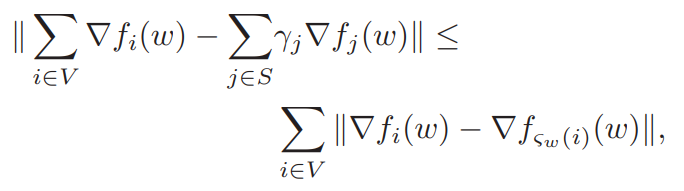
서브셋 선별 과정은 Algorithm1과 같다.

proof
Figure1은 다양한 IG(f SGD, SVRG, SAGA)방법론으로 모델을 학습한 결과이다. 제안하는 CRAIG 방식으로 subset을 사용하였을 때 가장 빠르게 학습하였으며, 최종적으로 달성한 error rate도 모든 데이터를 이용한 결과에 뒤쳐지지 않았다. 각 subset은 전체 학습 데이터셋의 10%를 사용하였으며 LIBSVM 데이터셋으로 실험하였다
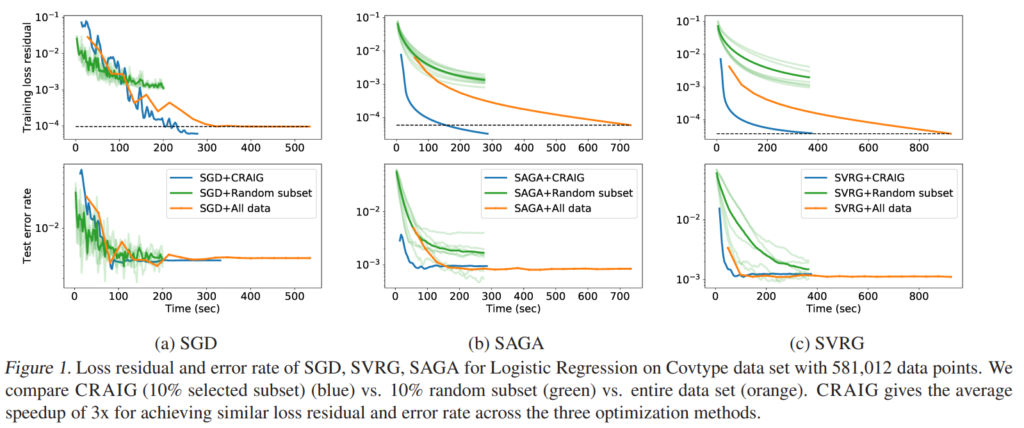
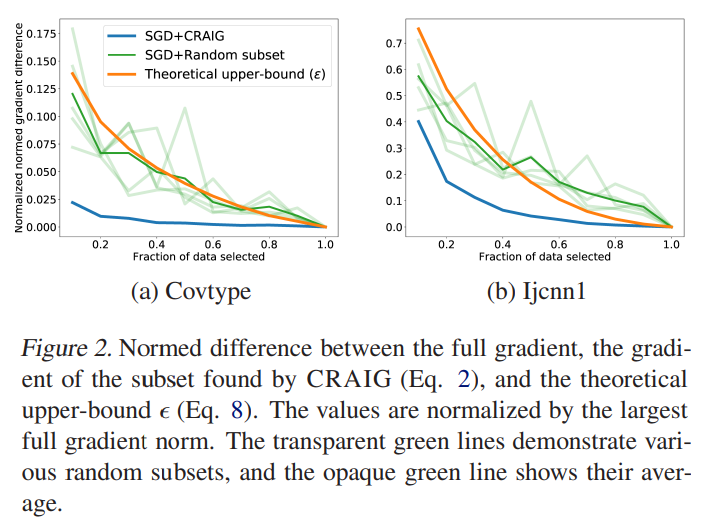
또한 Figure2를 통해 제안하는 subset이 학습의 안정성을 갖는다는것을 보였는데, random 데이터를 사용할때는 크게 변동하던 gradient가 CRAIG subset에서는 안정적인것을 보여, 제안하는 subset이 전체 데이터의 분포를 잘 반영하고 있음을 보였다.
제안하는 방법론으로 선별된 서브셋의 정량적 예시는 Figure6과 같다. 확실히 학습이 진행될수록 다양한 이미지를 선별함을 알 수 있다.

안녕하세요 리뷰 감사합니다.
성능을 위해 적은 데이터셋을 증강시키는 경우는 익숙하지만 subset을 통해 기존 데이터셋의 크기를 줄여 학습에 이용한다는 것은 익숙하지 않은 방식이라 새로운 개념을 알게 된 것 같습니다.
소개해주신 논문은 전체 데이터셋과 비슷한 학습 효과를 내는 서브셋을 찾는, 즉 전체 데이터셋을 대표하는 서브셋을 gradient 가중합의 유사도를 이용하여 알아내는 방법론이라고 이해하면 될까요?
또, Figure 1,2에서 random subset의 결과는 투명도가 다른 선 여러 개가 같이 그려져 있는데, 여러 번 학습한 결과와 그 평균값을 같이 표현한 건가요?
네 전체 데이터셋을 대표하는 서브셋을 gradient 가중합의 유사도를 이용하여 알아내는 방법론이 맞습니다.
다음으로 Figure 1,2의 결과도 말씀하신것처럼 여러 번 학습한 결과를 리포팅한 것 입니다.
감사합니다.