제가 이 논문을 읽어보게 된 이유는, 이전에 리뷰한 논문과 마찬가지로 여러 센서를 퓨전하여 이용할 때, 각 센서들의 문제가 생길 경우 어떻게 해결할 수 있는지를 찾아보기 위해 읽게 된 논문입니다. 이 논문은, Camera(Visual)와 IMU(inertial) 센서 뿐만 아니라 LiDAR 센서도 이용하는 방법론이었습니다. 또한, odometry 분야에서 각 센서별로 pose를 추정한 뒤 결합하는 loosely-coupled 방식과, 여러 센서의 feature를 결합하여 하나의 pose를 예측하는 tightly-coupled의 장점을 모두 이용한 방식이라 하여 읽어보게 되었습니다.

Introduction

지하 환경에서의 자율주행을 위해서는 GPS가 잘 작동하지 않는 상황에서 이를 대체한 위치인식 시스템이 필요하다. 이를 위해 LiDAR를 이용하는 연구들이 진행되었으나, LiDAR는 긴 터널이나 연기, 먼지 등의 공중 부유물로 인한 structure-less한 환경에서 잘 작동하지 않는 문제가 있다고 합니다. 여기에 카메라르 추가하더라도 카메라는 제한된 조도 환경에서 작동하는 문제가 있다고 합니다. 이렇듯이, LiDAR와 Visual(카메라), LiDAR-Visual 방식은 환경에 의존한다는 센서의 특성에 의해 강인성을 확보하기 어렵다는 문제가 있습니다.

또한, 센서들의 pose를 구하여 결합하는 loosely-coupled 방식은 쉽고 다른 센서로 확장이 가능하며, 연산량이 낮다는 장점이 있어 선호가 되는 방식이고,

각 센서들을 결합하여 하나의 pose를 에측하는 tightly-coupled 방식은 정확성이 높다는 장점이 있으나, 다른 센서로의 확장이 어렵고, 멀티 센서의 시스템 전환 방식이 어렵다는 문제가 있다고 합니다. 게다가, tightly-coupled 방식은 하나의 pose 추정 엔진을 이용하기 때문에 sensor failure 상황에 대응하기 어렵다는 문제가 있습니다. loosely-coupled 방식은 sensor failure에 대한 위험을 여러 pose 추정 엔진이 나눠가지기 때문에 보다 tightly-coupled 방식 보다 강인하다고 합니다. 이렇듯 두 방식은 각각의 장단점이 있고, 본 논문은 이러한 loosely-coupled 방식과 tightly-coupled 방식의 장점을 결합할 수 있는 방식을 제안하였다고 합니다.

또한, 해당 논문은 다른 센서들이 IMU의 편향을 제한한다면 이상치가 거의 없고 추정값이 정확하게 예측이 될 수 있을것이라는 insight를 기반으로 Super Odometry를 디자인하였다고 합니다. 여기서 IMU의 편향을 제한한다는 것은, 누적되는 오차를 제한한다는 것으로 우선 이해를 하였습니다.

논문의 Contribution을 정리하면 다음과 같습니다.

1. IMU를 중심으로하는 최초의 sensor fusion 파이프라인을 제안하여 극한의 어려운 상황에 정확한 예측이 가능하도록 함.
2. tightly-coupled 방식과 loosely-coupled 방식의 장점을 결합한 방식을 제안하여 간단하지만 효율적으로 센서를 결합함.
3. 3D points (dynamic octree)의 효율적인 구성을 scan사용하여 matching의 실시간 성능을 향상시킬것을 제안함.
4. 드론이나 지상 로봇을 포함한 여러 환경에 이용하며, 강렬한 움직임, low-light, 긴 복도(structure-less), 심한 먼지와 같은 환경에서 평가를 진행함.

System Overview

world frame은 \mathbf{W}, IMU body는 \mathbf{B}, LiDAR frame은 \mathbf{L}, camera frame은 \mathbf{C}로 표현합니다. 또한, 로봇의 k번째 상태\mathbf{x}_k는 아래의 식(1)로 표현되며, \mathbf{p}^w_{b_k}는 위치, \mathbf{v}^w_{b_k}는 속도, \mathbf{q}^w_{b_k}는 방향, \mathbf{b}_a와 \mathbf{b}_g는 각각 가속도와 자이로스코프의 bias를 의미한다고 합니다.

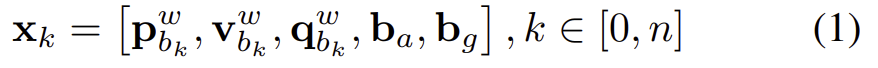
또한, 제안된 Super Odometry는 크게 3가지 부분으로 이루어져 있습니다: IMU Odometry와 VIO(Visual-inertial odometry), LIO(LiDAR-inertial odometry).

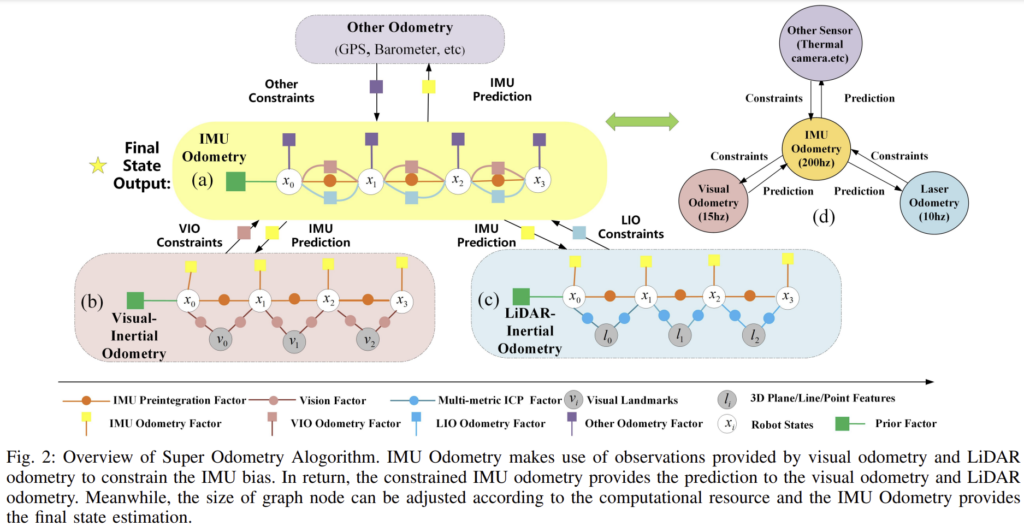
Fig. 2는 전체적인 오버뷰로, factor graph로 나타낸 것이라 합니다. VIO와 LIO를 이용하여 \mathbf{b}_a와 \mathbf{b}_g를 제한한다고 합니다. 반면 IMU odmetry는 VIO와 LIO에 예측을 제공하여 coarse-to-fine방식으로 motion을 복구하도록 한다고 합니다. 이제 조금 더 자세하게 알아보도록 하겠습니다.

A. IMU Odometry Factor

IMU Odometry는 Fig. 2의 (a)에 해당하며 위치와 속도, 방향 뿐만 아니라 가속도와 자이로스코프에 대한 bias도 포함합니다. pose의 각 그래프 노드는 state와 관련이 있으며, 연속된 두 pose 노드 사이의 edge(주황 동그라미로 표시됨)는 IMU preintegration 방식으로 구한 상대적 motion, 나머지 edge들은 센서에 따라서 local 혹은 global한 제약 조건이 될 수 있다고 합니다.

1)IMU Preintegration Factor

IMU preintegration 방식[1]에 의해 연속적인 i,j 사이의 상대적인 motion 측정값 \Delta \mathbf{r} = (\hat{\alpha}^i_j, \hat{\beta}^i_j, \hat{\gamma}^i_j) 을 얻을 수 있다고 합니다. IMU preintegration factor는 아래의 식(2)로 정의가 됩니다.

**[1]C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “Imu preintegration on manifold for efficient visual-inertial maximum-a-posteriori estimation.”

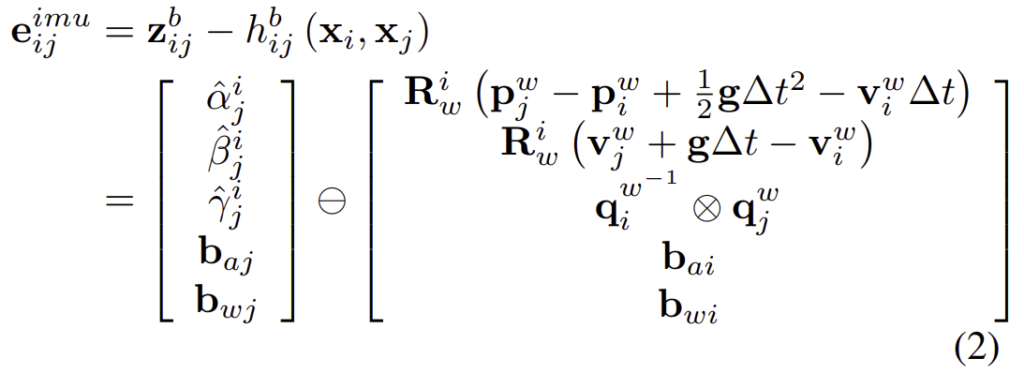
식을 간단하게 설명하자면 앞의 행렬인 \mathbf{z}^ b_{ij}는 i와 j 사이의 IMU preintegration을 통해 구한 상대적 motion과 bias이고, 뒤의 행렬은 GT가 됩니다. 또한, 두 bias는 함께 최적화가 된다고 합니다.

2) Relative Pose Factor

LiDAR와 카메라 odometry는 로봇의 초기 pose를 기반으로 pose를 local하게 알 수 있으므로, 상대 pose인 [\Delta p_j^i, \Delta q_j^i ]를 IMU preintegration의 위치 \hat{\alpha}^i_j와 rotation \hat{\gamma}^i_j의 제약조건으로 이용한다고 합니다. 또한, 그래프의 factor는 아래의 식으로 정의됩니다.

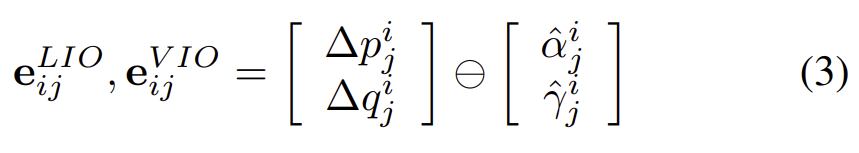
3) IMU Odometry Optimization

상대 pose factor는 관측치의 신뢰성을 기반으로 계산이 가능하도록 하기 위해 가중치 W를 부여합니다. 이 가중치W는 시각적 성능이 저하된 환경에서는 VIO의 가중치가 낮아지고, 기하학적으로 저하된 환경에서는 LIO의 가중치가 낮아지도록 합니다.

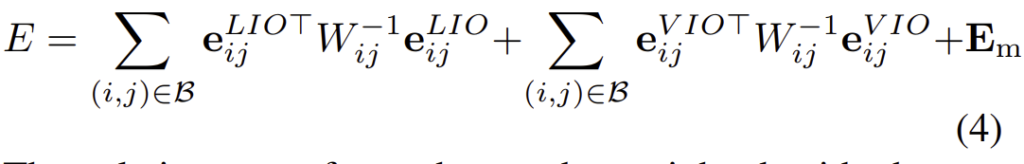
B. LiDAR-Inertial Odometry Factor

Fig. 2의 (c)에 해당하며, 계산적으로 효율적이고 높은 frequence를 가지는 IMU Odometry의 결과는 LiDAR-inertial odometry로 더해집니다. 이제 LIO의 작동에 대해 알아보겠습니다. LIO는 다음의 순서로 진행됩니다.

1) PCA Based Feature Extraction

LiDAR로 받은 point정보를 Down-Sampling하여 feature extraction 모듈로 넣는 과정입니다.

K-D tree 방식을 이용하여 구의 반경이 r에 해당하는 가장 가까운 k개의 neighbor point들을 찾습니다. 여기에 PCA를 적용하여 local linearity \sigma_{1D}, planarity \sigma_{2D}, curvatures \sigma_{3D}를 구하며, 이는 아래의 식으로 정의됩니다.

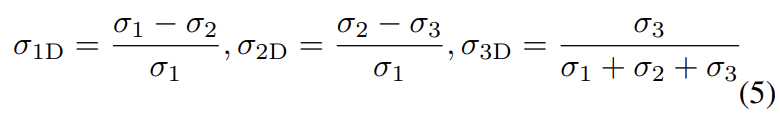
이때, \sigma_{i} = \sqrt{\lambda_i}이며 \lambda_i는 PCA의 고유값이 됩니다.

2)Multi-metric ICP Factors

IMU odometry에서 예측한 motion을 이용하여 \mathbb{F}_{i+1}(point, line, plane feature \mathbb{F}_{i+1} = {\{ F_{i+1}^{po}, F_{i+1}^{li}, F_{i+1}^{pl} }\} )는 \mathbf{B}에서 \mathbf{W}로 변환한뒤, 본 논문에서 제안된 dynamic octree를 이용하여 점,선,평면의 대응점을 찾습니다.

다음의 식(6)을 이용하여 point-to-point, point-to-line, point-to-plane의 오차를 한번에 최소화하여 최적의 변환을 예측한다고 합니다.

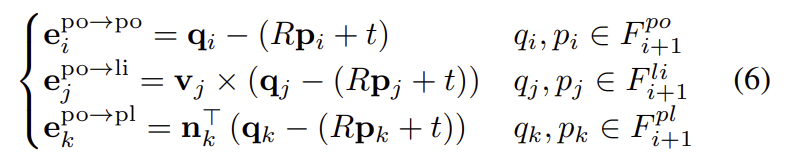
\mathbf{T}_{i+1} = \{ \mathbf{R,t} \} 는 예측하고자 하는 최적의 transformation입니다.

그러나, 먼지, 안개, 연기와 같은 공중 부유물에 의해, LiDAR로 얻은 기하학적 특징이 신뢰할 수 없다는 문제가 있습니다. 저자들은 추출된 형상의 주변 point가 점, 선 또는 평면 분포에 적합한지에 따라 대응점의 품질이 좌우된다는 것을 발견하였고, 분포의 품질 W_l = \{ w_i^{po→po}, w_i^{po→li}, w_i^{po→pl} \}은 아래의 식으로 정의하였습니다.

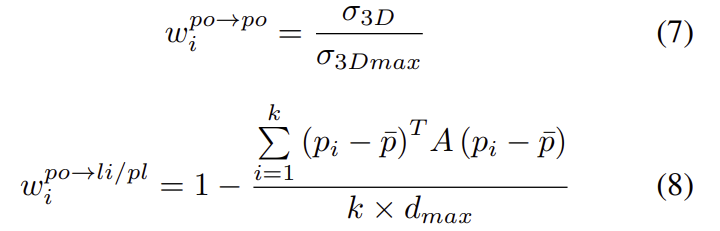
\sigma_{3Dmax}는 평면의 최대 threshold, p_i는 추출된 feature의 neighbor points, \bar{p}는 point들의 평균을 의미합니다. point-to-line(plane)에서 A = I - \mathbf{n}_k^{T} \times \mathbf{n}_k (A =\mathbf{n}_k^{T} \times \mathbf{n}_k) 이고, d_{max}는 point-to-line(plane)에 대한 최대 distance error를 의미한다고 합니다.

3)LiDAR-inertial Odometry Optimization

최적화 기법인 levenberg-marquardt 방식을 이용하여 최적의 transformation을 구한다고 합니다.

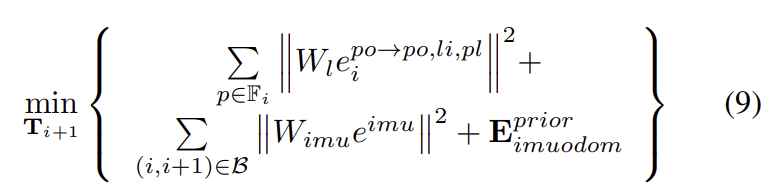
\mathbf{E}^{prior}_{imuodom}는 예측된 pose prior, \mathbf{e}^{imu}는 IMU odometry에서 구한 preintegration factor를 의미합니다. W_l, W_{imu}는 각각 LiDAR와IMU에 대한 가중치로, LiDAR의 입력을 신뢰하기 어려울 경우, LiDAR의 제약 조건의 품질 평가를 통해 낮은 가중치를 가지게 됩니다.

4) Dynamic Octree

대부분의 LiDAR SLAM은 KD-tree를 이용하여 3D 포인트를 정리합니다. 저자들은 이러한 전통적 KD-tree 방식은 하나의 tree만을 사용하고, 새로 point가 추가될 때 마다 KD-tree를 다시 생성해야 하므로 시간이 너무 많이 소요된다는 문제가 있다고 주장합니다. 이를 해결하고자, dynamic octree라는 효율적인 방식을 제안하였습니다.

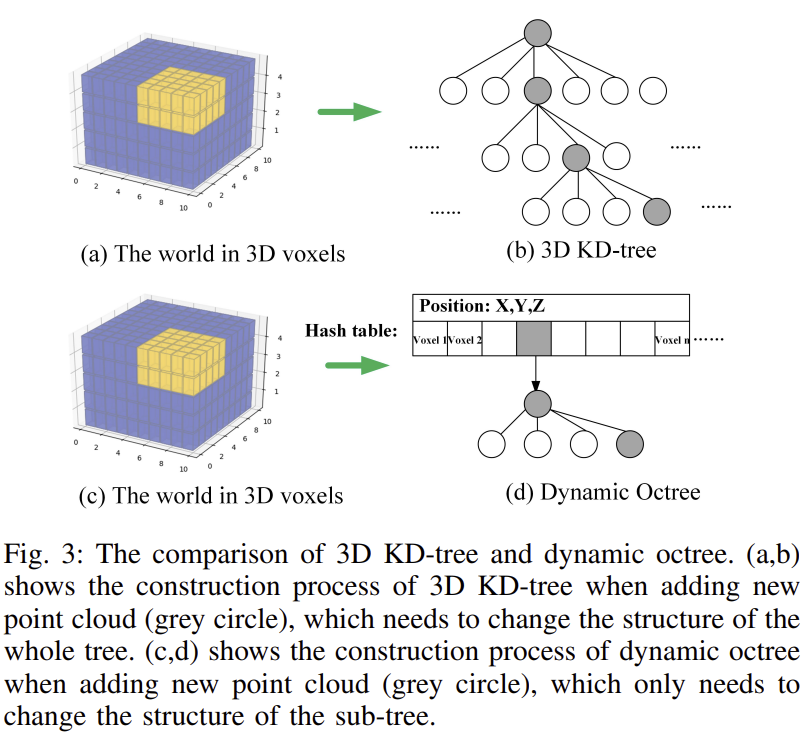
Fig. 3(d)와 같이, 맴을 hash 테이블로 저장하며, 하나의 tree만을 구축하는 대신 각 voxel에 point를 구성하는 octree가 있고, hash 테이블로 접근할 수 있습니다. 이후 업데이트를 할 때는 전체가 아닌 특정 octree만을 업데이터 하면 됙 ㅣ때문에 데이터 연결에 대한 실시간 성능이 향상된다고 합니다.

C. Visual-Inertial Odometry Factors

1) Visual-inertial Odometry Optimization

새로운 keyframe에 대하여 visual reprojection error \mathbf{e}_{reproj}, IMU preintegration factor \mathbf{e}_{imu}, marginalization factor \mathbf{E}_m으로 구성된 최적화를 진행하기 위한 수식은 아래와 같이 정의됩니다.

\mathbf{obs(i)}는 영상의 다른 프레임에에서 추적되는 시각적 특징 i를 포함하는 집합이고, 집합\mathbf{C}는 IMU factor로 연결된 노드 (a,b) 쌍을 포함한다고 합니다. 기하학 정보의 degradation과 마찬가지로, 시각 정보가 degradation이 될 경우 가중치가 낮아지고, 시각적 조건이 좋을 경우에는 최적화에 지배적인 역할을 하게 됩니다. 이때 IMU preintegration factor는 시각 feature의 추적을 위해 초기의 추정만을 제공하는 역할을 한다고 합니다.

Experiments

Super Odometry는 센서가 degradation이 된 경우의 강인성을 다른 SOTA 방법론들과 비교하고 실시간 성능을 평가하였습니다.

Dataset

test 데이터셋은 직접 촬영하였고, 아래의 Fig. 4에서 확인할 수 있습니다. 촬영된 데이터셋은 시각적/기하학적 degradation이 포함되어있습니다.

Robustness and Accuracy Evaluation

실험 결과는 아래의 TABLE Ⅱ를 통해 확인할 수 있습니다. LOAM과 LIOSAM은 LiDAR 기반의 방법론이고, VINS와 VINS-Depth는 Vision기반의 방법론을 의미합니다. 시각적/기하학적/시각&기하학적 degradation 상황을 고려한다고 합니다.

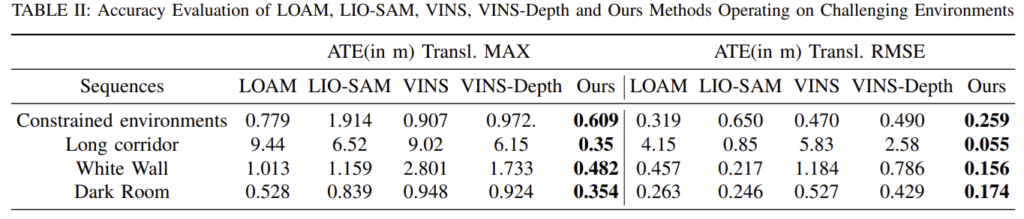
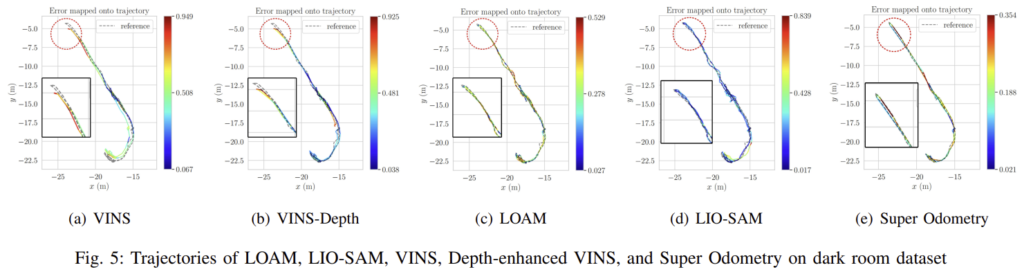
Visually Degradation

Dark Room에 해당하며, 어둡기 때문에 시각적 정보를 얻기 어렵습니다. Fig. 5가 궤적을 시각화한 것으로, vision기반의 방법론인 VINS에서 가장 안 좋은 결과를 보이고, 이는 표에서도 확인할 수 있습니다.

Geometrically Degradation

Long-Corridor에 대한 결과로, 이러한 시나리오는 건물 내부와 같은 인공적인 환경에서 흔하며, 반복적인 구조는 LiDAR 기반 알고리즘에서 문제가 될 수 있습니다. Fig. 6이 결과 Map을 시각화 한 것으로, LOAM과 LIO-SAM에서 드리프트가 발생한 것을 확인할 수 있습니다.(각 방법론의 1행 이미지들은 위에서 바라본 영상으로, 아래로 뻗어나온 점들 Super Odometry와 유사한 결과가 나와야 하는 데, (a)와 (b)는 포인트들이 잘 정렬되지 않은 결과가 나온 것으로 보입니다. 그런데 GT map을 같이 보여주지 않아서 이게 잘 나온 것인지는 판단이 잘 되지는 않습니다.. )

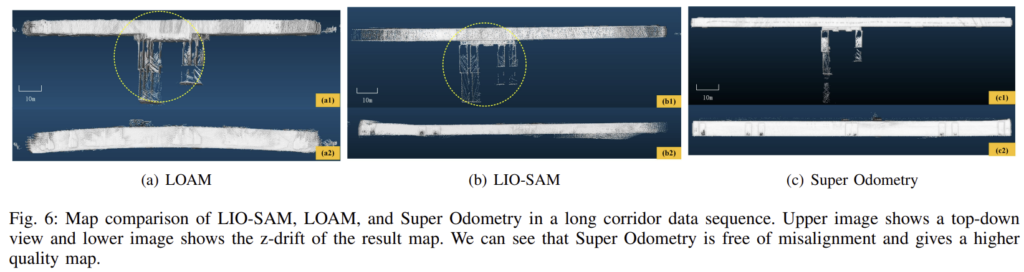
또한, 기하학적으로 degradation이 일어난 Constrained-Environment 상황에 대하여 실험을 하였고, 표를 통해 해당 논문의 방법론이 가장 좋은 성능을 나타냄을 확인할 수 있습니다.

Visually and Geometrically Degradation

이번에는 시각적으로와 기하학적으로 degradation이 발생한 경우인 Dust에 대한 실험 결과입니다.

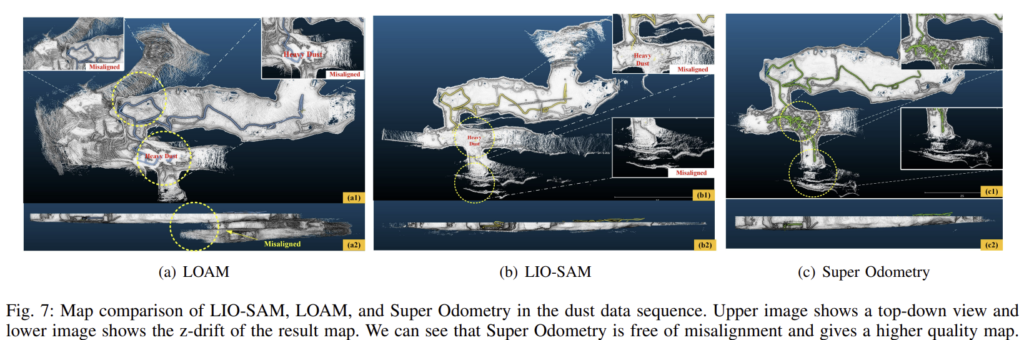
실험 결과, LOAM과 LIO-SAM 모두 정확한 Map을 만들지 못하였고 이는 Fig. 7을 통해 확인할 수 있습니다.

Real-time Performance Evaluation

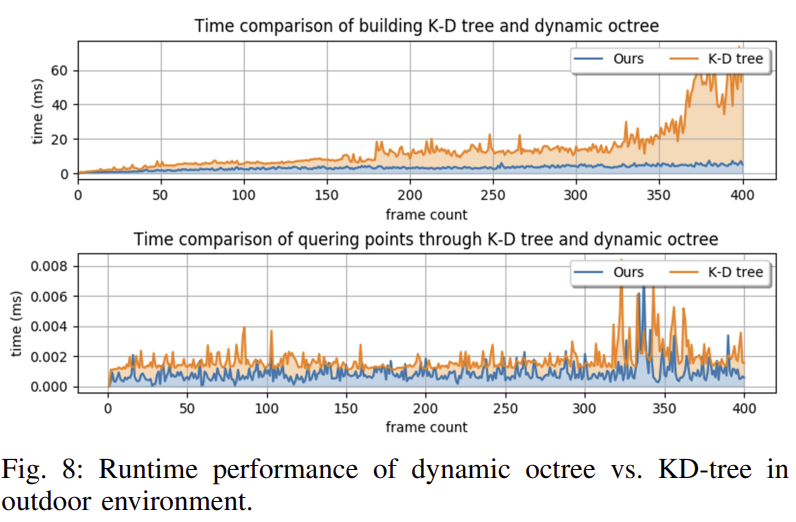
우선 시간을 줄이기 위해 논문에서 제안한 Dynamic octree를 이용하였을 때를 비교합니다. 아래의 Fig. 8을 통해 tree를 생성할 때와 찾을 때 모두 소요되는 시간이 확연히 줄어드는 것을 확인할 수 있습니다. 이는 앞서 언급했 듯이 dynamic octree는 전체 tree가 아닌 일부를 업데이트 하기 때문에 시간이 절약됩니다.

---

우선 이 논문에서 읽어본 적이 없는 LiDAR를 이용한 Odometry가 나와 읽는 데 오랜 시간이 걸렸습니다. 논문의 내용을 한줄로 정리하면 시각적, 기하학적 degradation 상황에서 품질 평가 과정을 통해 센서의 가중치를 조절할 수 있어 데이터 degradation 상황에서 강인한 결과를 얻을 수 있다라는 것입니다. 제가 해결하고자 하는 센서 slip 문제와는 거리가 있어 적용하기 어려울 것이라고 판단이 됩니다. 그러나 품질을 평가한다는 개념에 대하여 조금 더 고민해보려 합니다.