CVPR 논문 작업을 마치고, 주말 사이 다른 논문을 찾아볼 여유가 없어 이전에 제가 지난 학기 공부 했던 최적화 이론을 바탕으로 Geadient Descent 알고리즘에 대해 간단한(?) 수렴성 증명을 다루는 글을 작성해보도록 하겠습니다.
Convex Functions
Convex function의 정의에 대해서 다시 한번 상기시켜 보도록 하겠습니다. 우선 함수가 정의되는 정의역이 convex set 이어야 합니다. 그러한 상태에서 다음의 부등식을 만족하는 함수를 우리는 convex function이라 정의합니다.
- f(\theta x+(1-\theta )y)\leq \theta f(x)+(1-\theta )f(y),0\leq \theta \leq 1
여기서 등호가 사라지면 우리는 strictly convex function이라 정의합니다.
- f(\theta x+(1-\theta )y)<\theta f(x)+(1-\theta )f(y),0\leq \theta \leq 1

\theta x+(1-\theta )y는 x와 y사이에 존재하는 정의역입니다. 거기에 대응되는 치역이 f(\theta x+(1-\theta )y) 입니다.
\theta f(x)+(1-\theta )f(y)는 f(x)와 f(y)의 line segment입니다. 그래프로 보면 f(x)와 f(x)를 이어주는 선분으로 보면 됩니다.
이때, 저 부등식이 의미하는 것은 함수의 두 point로부터 만들어지는 line segment는 항상 함수의 값보다 크거나 작다라는 의미입니다.
Differentiable Convex Function
Convex function이 미분 가능해지면 가질 수 있는 성질에 대해서도 다시 한번 정리해보도록 하겠습니다.
First-order conditions
임의의 함수 f가 Convex 하고 1차 미분이 가능하다면, 꽤나 좋은 성질을 가지게 됩니다. 함수의 하한을 무조건 찾을 수 있기 때문입니다. 때때로 어떤 함수의 lower bound를 찾는 것이 어려울 수 있습니다. 하지만 함수가 Convex 하고 일차 미분이 가능하다면 1차 테일러 근사를 통해서 global underestimator를 얻을 수 있는 것이지요.
- f(x)+\nabla f(x)^{T}(y-x)\leq f(y)
위의 부등식을 얻을 수 있는데 이는 함수의 lower bound를 보장해주는 부등식이라 볼 수 있습니다. (n=1)이라면 우리가 잘 알고 있는 일변수 형태의 f(x)+f^{\prime }(x)(y-x)\leq f(y) 익숙한 부등식을 얻을 수 있습니다.

그림을 보면 알겠지만 x라는 포인트에서 일차 테일러 근사를 구했을 때, 그 근사치는 항상 원래 함수보다 작다는 것을 알 수가 있습니다. 아직 convex optimization에 대해서 자세히 공부를 한 것은 아니지만, 책에서는 이 일차 미분 성질이 convex function의 아주 중요한 성질이라고 강조를 하고 있습니다. 임의의 함수가 Convex function이라면 \nabla f(x)=0이 global minimum이기 때문이죠.
중요한 성질인 만큼 증명도 같이 한번 해보고 넘어가도록 하겠습니다. 우리가 증명하고 싶은 명제는 다음과 같습니다.
” 미분 가능한 Convex 한 함수는 f(x)+\nabla f(x)^{T}(y-x)\leq f(y)를 만족한다.”
정말로 그러한지 보도록 하겠습니다. 간단하게만 진행하기 위해 (n=1)인 일변수 함수에 대해서만 해보도록 하겠습니다.
먼저 f가 convex 하므로 우리는 아래의 부등식을 얻을 수 있습니다.
- f(tx+(1-t)y)\leq tf(x)+(1-t)f(y),0\leq t\leq 1
여기서 양변을 t로 나눠주고 이항을 조금 해주면 아래처럼 만들 수 있습니다.
- f(x)+\frac{f(x+t(y-x))-f(x)}{t} \leq f(y)
여기서 t\rightarrow 0 극한을 취해주면
- f(x)+(y-x)\lim_{t\rightarrow 0} \frac{f(x+t(y-x))-f(x)}{t(y-x)} \leq f(y)\Longrightarrow f(x)+f^{\prime }(x)(y-x)\leq f(y)
원래 일차 미분 부등식을 얻을 수 있습니다. f가 convex 하다면 이 부등식을 유도할 수 있으니, 이제는 반대로 이 부등식을 가지고 f가 정말 convex 한지 알아보도록 하겠습니다. x!=y,0\leq \theta \leq 1,z=\theta x+(1-\theta )y를 가정했을 때 두 가지 부등식을 얻을 수 있습니다.
- f(z)+(x-z)f^{\prime }(z)\leq f(x) … (1)
- f(z)+(y-z)f^{\prime }(z)\leq f(y) … (2)
여기서 첫 번째 부등식에는 \theta를 두 번째 부등식에는 1-\theta 를 곱해주고 각자 더해주면 아래의 결과를 얻을 수 있습니다.
- \theta f(z)+\theta (x-z)f^{\prime }(z)+(1-\theta )f(z)+(1-\theta )(y-z)f^{\prime }(z)\leq \theta f(x)+(1-\theta )f(y)
- f(z)(\theta +1-\theta )+f^{\prime }(z)(\theta x-\theta z+y-z-\theta y+\theta z)\leq \theta f(x)+(1-\theta )f(y)
- f(z)=f\left( \theta x+(1-\theta )y\right) \leq \theta f(x)+(1-\theta )f(y)
부등식을 다 정리해보면 우리가 알고 있는 Convex Function의 정의를 띠고 있습니다. 고로 증명이 완료되었습니다.
Second-order conditions
임의의 함수 f가 Convex 하고 2차 미분이 가능하다면(Hessian Matrix가 존재) 함수의 2차 미분이 모든 정의역에 대해 항상 양의 값을 가진다면 임의의 함수는 Convex Function이라 할 수 있다 입니다. 그 역도 성립합니다.
조금 더 간단하게 생각해보겠습니다. 우리가 고등학교 때 수학 시간 때 미적분을 잘 배웠다면 함수가 아래로 볼록하기 위해서는
- 0\leq f^{\prime \prime }(x)
라는 조건이 필요했습니다. 이계도함수가 항상 양수라는 것은 함수의 도함수는 단조 증가한다는 의미입니다. 도함수가 단조 증가하기 위해서는 아래의 그림과 같은 그래프의 모양이어야 합니다.

같은 맥락입니다. n=1이 아닌 경우의 함수의 이차 미분은 Hessian Matrix를 통해 얻을 수 있을 것입니다.
- 0\preceq \nabla^{2} f(x)
즉, 임의의 함수 f:R^{n}\rightarrow R의 Hessian Matrix가 Positive semi definite라면 함수 f는 Convex 합니다. 역도 성립하기 때문에 이 성질을 이용하여 우리는 처음 보는 함수의 Convexity를 증명하는 데 사용할 수 있습니다.
사실 Hessian Matrix를 구하는 것은 단순 미분이기 때문에 어렵지는 않지만 그 Hessian이 Positive semi definite라는 것을 보이는 것은 쉽지 않기 때문에 상황에 따라 사용하면 됩니다.
참고로 Hessian Matrix가 Positive definite라면 함수 f는 strictly convex입니다. 하지만 이 경우에는 역은 성립하지 않습니다.
L-smooth function
우리는 다음의 함수를 L-smooth function이라고 정의합니다.
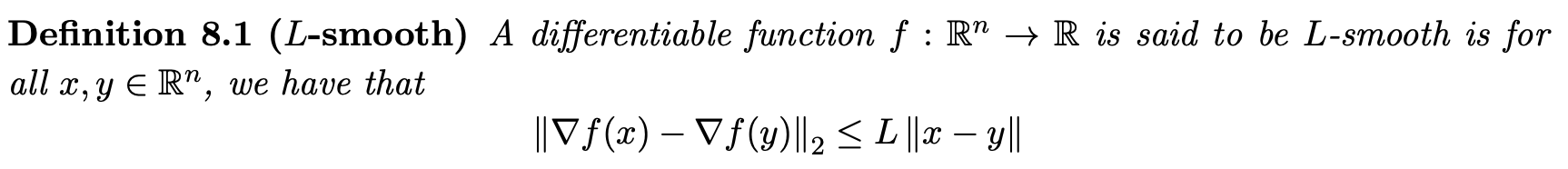
간단하게 말하면 gradient가 립시츠 연속성을 가지는 함수를 smooth function이라고 정의합니다. 복잡하게 얘기하지 않고 직관적으로 설명하자면 gradient의 변화율이 상한선을 가지게 된다는 의미입니다. gradient가 빠르게 변하지 않기 때문에 gradient descent 입장에서는 발산하는 등의 문제를 막는데 좋은 성질로 작용하게 됩니다.
관련된 보조 정리도 하나 설명하도록 하겠습니다.

f가 위로 quadratic 함수로 bound 되어있다는 의미입니다. 아래의 그림처럼 말이죠

즉, f는 너무 sharp 해질 수 없고, 빠르게 변화할 수 없음을 의미합니다.
Convergence Analysis for convex and smooth objective function

우리의 목적함수가 convex function이며 미분이 가능하다고 가정하고, gradient가 립시츠 연속성을 가진다고 가정하겠습니다. 이럴 때 fixed step size(고정된 learning rate)에 대해서 gradient descent가 수렴할 수 있음을 보이도록 하겠습니다.

그리고 목적함수가 L-smooth function이기 때문에 위의 부등식이 성립하게 됩니다.

그리고 이제 gradient desecent의 update rule(x^{+}=x-t\nabla f(x))을 이용하여 식을 전개해보겠습니다.
update rule에 따라서 y=x^{+}=x-t\nabla f(x) 대입해주고 식을 조금 정리해주도록 하겠습니다.
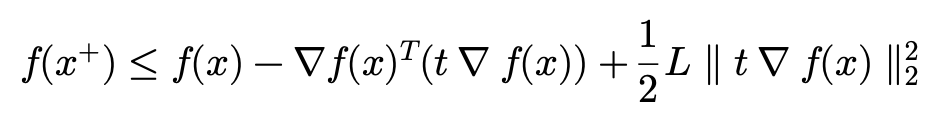
t를 앞으로 빼주고 \nabla f(x)에 대해서 정리해주면
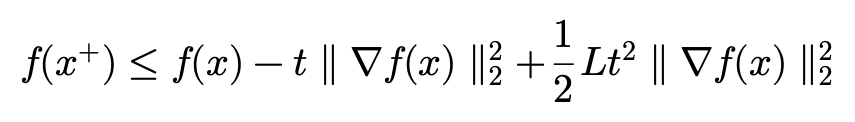
다음에는 공통 인수로 묶어주겠습니다.
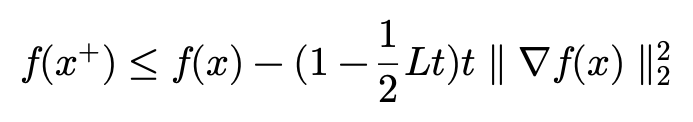
여기서 -1(1-\frac{1}{2} Lt)에 집중해보면 t\leq 1/L을 만족할 때 upper bound를 구할 수 있습니다.
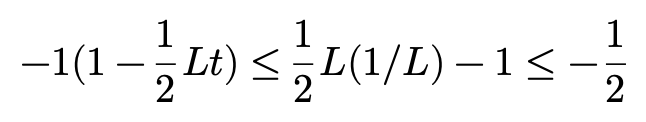
그래서 -1(1-\frac{1}{2} Lt)를 -\frac{1}{2} 로 치환하겠습니다. 부등호는 그대로 유지가 됩니다.

그리고 여기서 f가 convex function이고 미분 가능하기 때문에 first-order condition을 통해 f(x^{+})를 f(x^{\ast })를 가지고 bounding 할 수 있습니다. 여기서 f(x^{\ast })는 우리가 찾고자 하는 optimal value입니다.
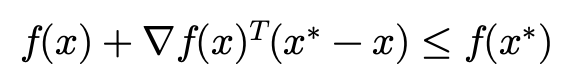
조금 부등식을 조작해서 f(x)에 대해서 정리해주면 다음과 같습니다.
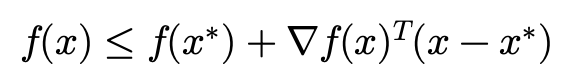
그리고 얻은 f(x)에 대한 부등식을 이용해 f(x^{+})에 대한 새로운 bound를 얻을 수 있습니다.

그리고 \frac{1}{2}로 묶어서 간단한 식 조작을 해주도록 하겠습니다.

그리고 \parallel x-x^{\ast }\parallel^{2}_{2} 더 했다가 빼주도록 하겠습니다.
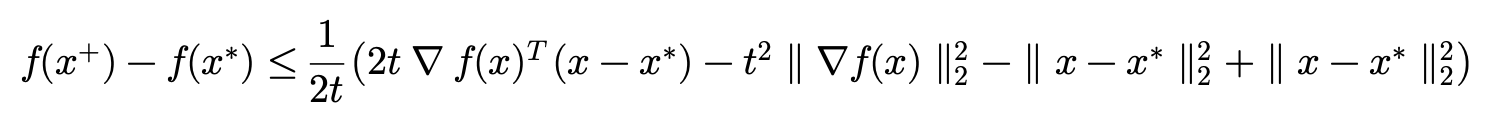
여기서 \parallel x-t\nabla f(x)-x^{\ast }\parallel^{2}_{2} =\parallel x-x^{\ast }\parallel^{2}_{2} -2t\nabla f(x)^{T}(x-x^{\ast })+t^{2}\parallel \nabla f(x)\parallel^{2}_{2} 이 성립하기 때문에 부등식을 다시 정리할 수 있습니다.

gradient descent의 update rule(x^{+}=x-t\nabla f(x))에 따라서 다시 식을 정리하면 아래와 같습니다.
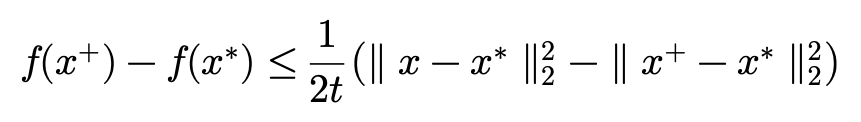
이제 부등식을 iteration에 따라 summation을 취해주도록 하겠습니다.
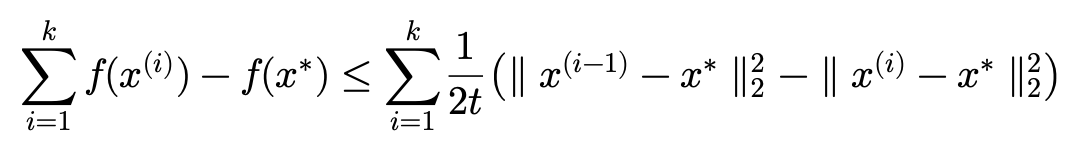
우변(Right Hand Side)는 망원급수(telescoping series)라 불리는 형태이기 때문에 시그마를 전개해주면 두 개의 항만 남게 됩니다.
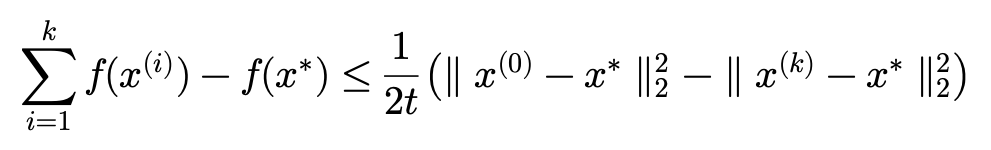
그리고 당연히 아래와 같이 다시 부등식을 정리할 수 있습니다.
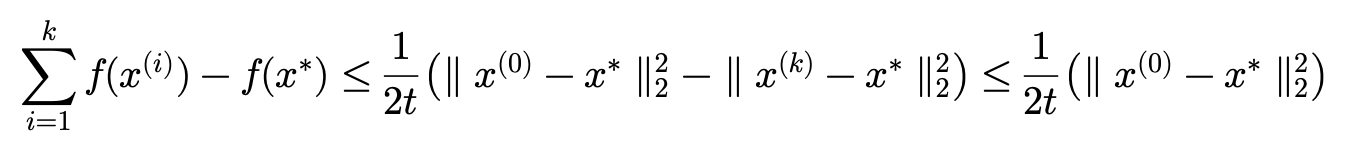
그리고 최종적으로 부등식을 정리하면 증명이 마무리됩니다.
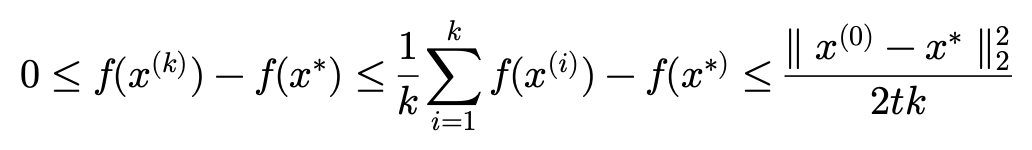
여기서 iteration(k)를 무한으로 보내면 샌드위치 정리에 의해 f(x^{\ast })로 수렴할 수 있음을 알 수 있습니다. 좌우가 0으로 갇혔기 때문에 f(x^{(\infty )})=f(x^{\ast }) 이 성립합니다.
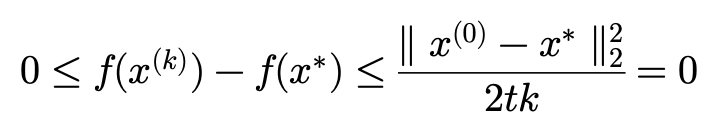
이상으로 미분 가능한 Convex function이며 L-smooth 함수에 대해서 Gradient Descent 알고리즘의 Convergence Analysis에 대해서 알아보았습니다.
다양한 상황에서 다양한 알고리즘에 대해 Convergence Analysis를 정리하는 것은 시간이 날 때 차차 해보도록 하겠습니다.
포스팅을 마치도록 하겠습니다. 감사합니다.