논문 쓰느라 정신이 없어 X-리뷰를 한동안 작성하지 않았는데 오랜만에 작성하게 되네요 허허. 이번에 가져온 논문은 이번 CVPR2022에 게제된 Iterative Deep Homography Estimation이란 방법론이며 제목 그대로 호모그래피를 iterative한 방식으로 refine하여 정확하게 추정하겠다는 것이 해당 논문의 contribution입니다.
Intro
인트로에 대해서는 조금 간략하게 작성을 해보려고 합니다. 먼저 해당 논문에서 정의한 문제는 대략적으로 2가지 정도 있는 것 같습니다.
먼저 기존의 iterative하게 호모그래피를 추정하는 방법론들은 VGG-style network를 cascading 형식으로 쌓아서 학습을 하는 것을 의미했습니다. 즉 source와 target image를 넣고 구한 호모그래피를 다시 source 영상에 적용해 warping을 시키면, 해당 warping된 이미지와 다시 target image를 2번째 네트워크에 넣고 또 새로 구한 호모그래피를 한번 더 warping하느 식으로 반복을 하는 것이죠.
이렇게 하게 될 경우 물론 더 정확한 호모그래피를 구할 수 있겠으나, iteration 횟수를 늘리기에는 메모리 관점에서 한계가 있을 것이며 또한 무작정 개수를 늘린다고 한들 성능의 향상을 보장할 수 없다고 합니다.
그래서 최근에 나온 방식으로는 Lukas Kanade라고 하는 아주 예전에 optical flow의 기초가 되는 알고리즘을 Deep learning과 연계한 방법론이 있습니다. 이 방법 역시 성능은 우수했으나 아쉬운 점은 Lukas Kanade라는 알고리즘은 결국 untrainable한 방식이기 때문에, 결국 feature map으로 활용할 CNN encoder만 학습을 한다는 점에서 그 자체로 단점이 존재한다는 아쉬움을 얘기합니다.
그래서 저자는 모든 framework이 딥러닝 기반의 썸띵으로 이루어진 새로운 방법론을 제안하게 됩니다. 간략하게 저자의 기여를 소개드리면 저자가 새롭게 제안한 Iterative Homography Network(IHN)은 구성 자체가 완벽하게 학습이 가능하며 반복적으로 수행함에도 불구하고 학습 및 추론 결과가 안정적으로 수행된다고 합니다.
또한 네트워크의 구성도 효율적으로 설계하여 상당히 경량화가 잘 되었으며 추론 속도 역시 기존의 iterative homography estimation methods들과 비교하여 상대적으로 빠른 추론 속도를 보인다고 저자는 주장합니다.
보다 자세한 내용들은 아래 method에서 설명하도록 하겠습니다.
Method
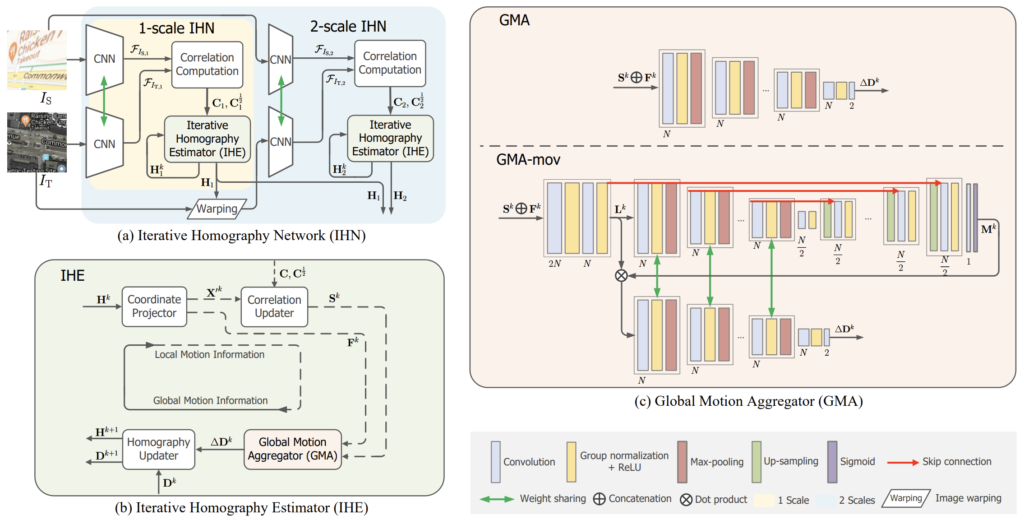
일단 논문에서 제안하는 contribution들은 모두 그림2에서 확인할 수 있습니다. 입력은 당연히 호모그래피를 추정해야하기 때문에 source image I_{s}와 target image I_{t}가 활용됩니다. 해당 방법론의 큰 흐름은 먼저 CNN을 통해 feature map을 추출하고, 두 feature pair에 대하여 correlation을 계산한 다음, 해당 논문의 핵심인 iterative homography estimator(IHE)를 들어가게 됩니다.
Feature Extraction
그럼 가장 첫번째 단계인 feature extraction부터 살펴보겠습니다. 먼저 feature encoder는 Siamese 형식의 CNN을 활용하고 있으며, 해당 CNN를 구성하는 basic unit은 1개의 max-pooling layer(stride2)와 2개의 residual block으로 구성이 되어있습니다.
먼저 Resnet과 동일하게 제일 첫번째 conv layer는 7×7 커널사이즈를 가지고 있으며 그 후 q개의 basic unit을 통과하여 feature map을 추출합니다. 하나의 basic unit에는 2 stride의 max-pooling을 가지고 있으니 2배 다운 샘플링이 진행될 것이며 즉 q의 개수에 따라서 영상의 해상도는 \frac{1}{2^{q}}로 줄어들게 됩니다. 마지막으로 1개의 1×1 conv layer를 통과하게 되면 최종적으로 feature map이 생성됩니다.
저자는 1-scale IHN의 경우에는 q를 2로 설정하였으며, 만약 2-scale IHN이라면 역시 q값은 2라서 feature map이 4배 다운샘플링이 되지만 호모그래피를 계산할 때 1/2 scale feature map과 1/4 scale feature map을 모두 사용한다고 합니다.
Correlation
다음은 correlation map 관련된 내용입니다. 사실 이 correlation이라는 개념은 visual correspondence를 풀고자하는 분야에서 정말 많이 사용하는 개념입니다.(보통 localization 쪽 분야들이 많이들 관심있어하죠.)
이러한 correlation map은 정말 간단하게 구할 수 있는데, 먼저 source image와 target image의 feature map을 각각 (\mathcal{F}_{I_{s}}, \mathcal{F}_{I_{t}}) \in \mathbb{R}^{D \times H \times W} 이라고 정의할 수 있습니다. 그러면 이제 두 feature map에 대한 correlation map은 다음과 같이 계산할 수 있습니다.
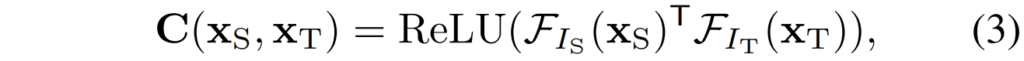
여기서 ReLU를 취한 이유는 correlation map은 결국 상관관계를 나타낸 것이므로 음수 값은 의미가 없다고 판단하여 적용한 것 같습니다. 아무튼 이렇게 만들어진 C의 차원은 결국 H x W x H x W가 되는데, 이는 correlation map이 각 feature map의 픽셀 하나하나의 dimension을 서로 곱하여 spatial 차원에 대한 attention map을 계산했다고 생각하시면 좋을 것 같습니다.
Correlation Pooling
이렇게 계산된 Correlation은 일단 feature map이 원본 영상의 1/4 스케일이다보니 해상도도 크고 너무 local level에서의 correlation이 계산되었다고 볼 수 있습니다. 그래서 저자는 수식3을 통해 계산한 correlation map에다가 stride2의 average pooling을 수행하여 C^{\frac{1}{2}} \in \mathbb{R}^{H \times W \times H/2 \times W/2} 를 계산하게 됩니다. 이는 기존의 Corrleation map보다 더 넓은 인지 범위를 가질 수 있다고 합니다.
Iterative Homography Estimation
그럼 본격적으로 저자가 제안하는 메인 모듈에 대한 설명을 들어가도록 하겠습니다. 먼저 그림2-(a)와 (b)에서도 확인할 수 있듯이, IHE 모듈은 먼저 C, C^{\frac{1}{2}} 를 입력으로 하여 두 영상의 호모그래피 H를 계산하는 것이 목표입니다.
여기서 저자는 coordinate projector부터 global motion aggregator의 과정을 통해 loca motion information을 통합하여 global homography estimation을 수행한다고 주장하며, k번째 global motion aggregation부터 k+1번째 coordinate projector의 과정을 통해 global homography가 local information을 업데이트한다고 합니다.
Coordinate Projector
그럼 먼저 Coordinate Projector에 대해서 알아보겠습니다. 해당 컨셉은 먼저 k번째 iteration 관점을 예로 들면, source feature map과 target feature map 사이에 point-wise correspondence는 \mathbf{H}^{k}를 통해 그 관계를 나타낼 수 있습니다.
보다 구체적으로 source feature map의 meshgrid coordinate를 \mathbf{X} , target feature map의 meshgrid coordinate를 \mathbf{X'} 라고 두었을 때, 저희는 각각의 픽셀 좌표를 \mathbf{x} = (u, v) , \mathbf{x'} = (u', v') 로 나타낼 수 있습니다. 그러면 수식적으로 두 source, target pixel과 \mathbf{H}^{k} 의 관계는 다음과 같이 나타낼 수 있습니다.
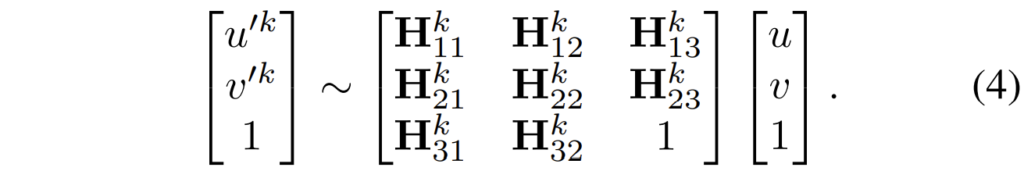
사실 수식 4에 대한 과정은 호모그래피를 알고 계신다면 당연한 내용이지만, 굳이 해당 내용을 한번 더 넣은 이유는 뒤에서 설명드릴 Global Motion Aggregator(GMA)라는 모듈의 입력으로 correation과 함께 flow map을 함께 넣기 때문입니다.
여기서 이 flow map은 아래 수식과 같이 구할 수 있습니다.
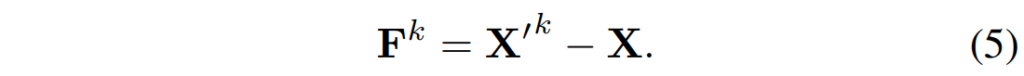
즉 k번째 iteration에서의 target coordinate \mathbf{X'}^{k} 와 그냥 기본 source coordinate 간에 meshgrid를 뺀 것이 바로 flow map \mathbf{F}^{k} 입니다. 그리고 저 \mathbf{F}^{k}는 위에서도 말했듯이 GMA 모듈의 입력으로 보내집니다.
Correlation Updater
Correlation Updater는 Correlation volume C를 호모그래피를 이용해 sampling 및 update하는 과정을 의미합니다. 사실 이 부분에 대해서는 논문에서 한 문단으로 짧게 설명이 되어있으며 왜 이 모듈이 필요한지, 무엇을 의도했는지에 대한 설명이 불분명해서 자세하게 설명드리기는 어려울 것 같습니다. 일단 샘플링 과정은 아래 수식처럼 진행이 될 수 있습니다.
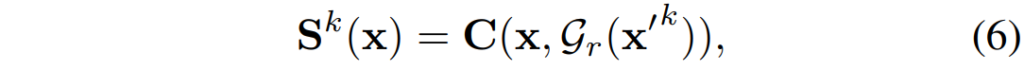
여기서 \mathcal{G}_{r}(\mathbf{x'}^{k}) 는 고정된 서칭 범위 r만큼의 local square grid를 의미합니다. 그림으로 표기하면 그림3과 같이 진행된다고 하는데 이 부분은 그림도 모호하고 설명도 부실한게 아무리 읽어도 도입 의도를 잘 모르겠네요:(
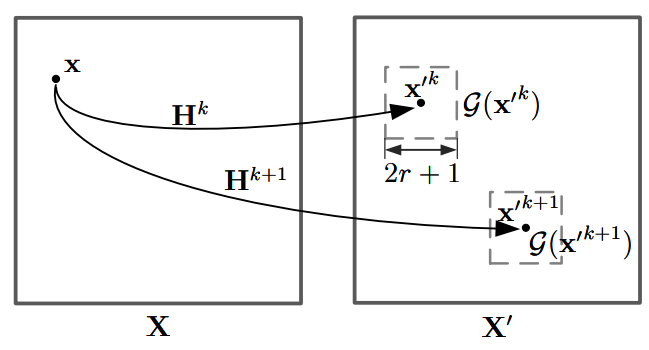
참고로 C^{\frac{1}{2}} 에 대해서도 동일하게 correlation updater를 적용한다고 합니다. 제가 생각했을 떈 이 correlation updater는 결국 iteration을 반복하면서 최적의 호모그래피를 근사화하는 과정이기 때문에 매 iteration 마다 구했던 호모그래피를 통해 flow map을 새로 계산하고, 새롭게 계산된 flow map에 맞게 기존 correlation map을 업데이트하는 과정이 아닌가 라는 생각이 듭니다. (근데 그러면 왜 fixed search radious라는 개념을 활용하는 건지는 애매하네요.)
Global Motion Aggregator(GMA)
다음은 GMA 모듈에 대한 설명으로 결론부터 말씀드리면 해당 모듈은 위에서 계산한 수식 6에서 계산한 correlation slice와 flow map을 입력으로 받아 이 테스크의 목표인 호모그래피를 계산하는 모듈입니다. 여기서 한가지 짚고 넘어가야할 점이 있다면, 사실 호모그래피 추정 분야는 지난 번 관련 분야 리뷰에서도 다뤘다시피 3×3 호모그래피 행렬을 바로 추정하지 않습니다.
이는 호모그래피 행렬 값 하나하나의 scale 값이 다 다르기 때문에 모델의 수렴이 어려워서 모델이 잘 학습되지 않기 때문으로, 따라서 해당 분야에서는 호모그래피 행렬 자체를 예측하는 것보다는 source imaeg에 대한 대응되는 target point 집합을 구하는 방식으로 호모그래피를 예측합니다.
즉 source image의 각 코너 점 4점을 source points로 본다면 모델은 해당 source points에서 얼마만큼의 distance를 더하면 target points가 되는지를 나타내는 offset을 예측한다고 보시면 될 것 같습니다. 이렇게 자세하게 얘기한 이유는 당연히 GMA의 output 역시 4점에 대한 offset을 예측하는 것이기 때문입니다.
아무튼 이러한 GMA는 또 2가지 type으로 나뉘는데, 그림2-(c)에서 볼 수 있듯이 그냥 GMA가 하나 있고 GMA-mov 라는 것이 하나 또 있습니다. 그냥 GMA는 stactic scean 전용 모듈이라고 볼 수 있으며, GMA-mov는 동적인 물체가 있는 장면에서 더 좋은 성능을 보여주는 모듈이라고 이해하시면 되겠습니다.
먼저 GMA부터 살펴보면 GMA 역시 basic unit이라는 개념이 존재하고 이 basic unit이 다중으로 쌓여있는 것을 확인하실 수 있습니다. basic unit의 구성은 3 x 3 conv block, 1 group normalization, ReLU, 그리고 stride 값이 2인 max-pooling으로 구성되어 있습니다.
해당 basic unit은 입력으로 사용한 correlation map과 flow map이 2×2의 해상도를 가질 때 까지 반복을 하게 됩니다. 그리고 나서 최종적으로 채널 축까지 2로 projection하여 2 x 2 x 2라는 tensor가 나오도록 합니다. 이는 4개의 포인트에 x, y에 더해줄 offset을 의미하게 됩니다. 논문에서는 해당 결과물을 \triangle \mathbf{\mathcal{D}}^{k}라고 합니다.
그러면 이제 GMA-mov에 대해서도 알아보겠습니다. 사실 GMA-mov도 GMA에 그냥 decoder가 있는 버전이다 라고 생각하시면 될 것 같습니다. Unet처럼 Encoder-Decoder 구조를 둔 이유는 Decoder를 통해 동적인 객체들을 제거하는 ransanc filter 같은 개념이라고 볼 수 있는데, 엄밀히 말하면 decoder에서 타고 나온 1채널 feature map에 sigmoid 연산을 통하여 0~1사이의 분포를 가지는 값을 만들게 됩니다.
이렇게 만들어진 outlier filter는 GMA-mov의 초반부에서 취득한 \mathbf{L}^{k}에 dot-product을 수행하여 동적인 객체들은 제거한다고 보시면 될 것 같습니다. 이러한 동적인 객체들은 정확한 호모그래피를 추정하는데 있어 방해 요소로 많이 작용하기 때문에, 기존의 호모그래피 추정 방법론들에서도 활용을 하고 있었는데 이미지 레벨에서 마스크를 추출하는 이전 방법론들과 달리 correlation map과 flow를 통하여 mask를 계산하였다는 차별점이 있습니다.
Homography Updater
이제 마지막으로 GMA모듈까지 통과하여 k번째에 해당하는 offset을 계산하였다면 k+1번째로 향하기 위해 offset을 update해주어야만 합니다. 해당 과정은 아래 수식처럼 진행이 됩니다.
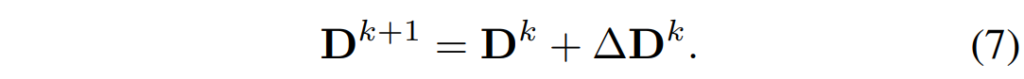
그냥 현재 target points에 offset을 더한 것이 k+1번째의 target points다 라는 것을 표현한 것으로 상당히 직관적입니다.
Loss Function
해당 방법론은 supervised 방법론이기 때문에 학습을 위한 loss값은 GMA 모듈에서 예측한 offset과 GT offset 사이에 norm값을 계산하게 됩니다. 해당 loss는 iteration 수 만큼 반복해서 평균을 계산하게 되며 만약 2stage까지 진행이 된다면 multi scale로 loss가 계산됩니다.
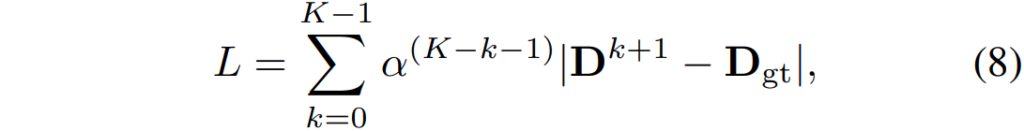
Experiments
논문에서는 크게 4가지 데이터 셋으로 성능을 평가하였습니다. 가장 대표적으로 많이 활용되는 MS-COCO dataset, 그리고 moving object가 많아서 어려운 장면들로 구성된 SPID surveillance dataset, 그리고 google map과 이에 대응되는 위성사진 셋으로 평가를 진행합니다.
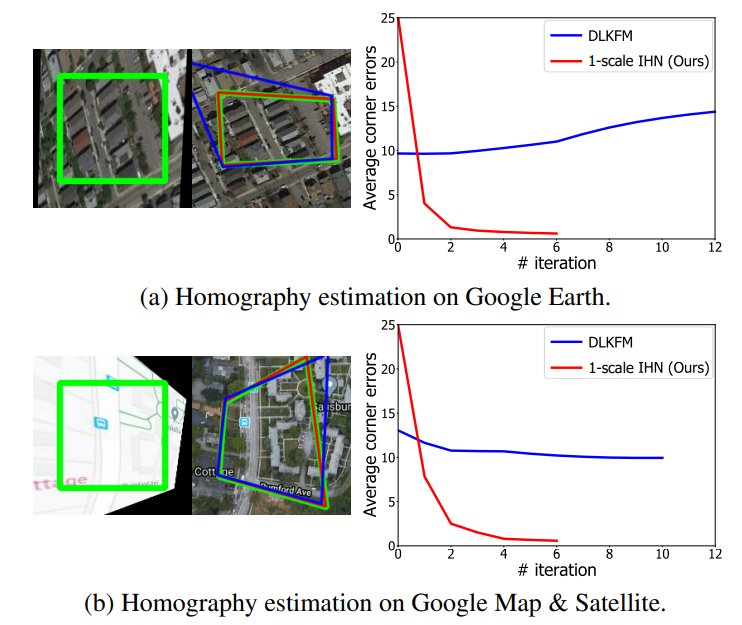
정량적 성능 결과는 아래 그래프를 통해 확인하실 수 있습니다. 아무래도 평가용 데이터 셋이 많다 보니, 테이블 형식이 아닌 그래프로 표현한 것 같은데 생각보다 직관적이지 않아 보기가 힘드네요.
일단 평가 메트릭으로는 Average corner error를 활용합니다. 이는 모델이 예측한 offset과 실제 target points의 픽셀 좌표의 오차라고 이해하시면 될 것 같습니다. 그리고 당연히 오차이기 때문에 값이 작을수록 좋은 것이기에 그래프들이 좌x축 기준 좌측으로 쏠릴 수록 더 적은 에러 값을 가지면 좋은 것 같습니다.
저자가 먼저 강조하고 싶은 부분은 MSCOCO 데이터 셋 기준으로 자신들이 제안한 IHN을 1scale만 적용하였을 때 CLKN과 LocalTrans를 제외한 모든 방법론들보다 성능이 더 좋다고 주장합니다. 그리고 2-scale로 진행할 경우 앞에 두 개의 방법론들보다 더 좋은 성능을 보여줄 수 있었구요.
그리고 저자는 아래 테이블에서 볼 수 있듯이, MSCOCO dataset에서 ablation study도 진행하였습니다.
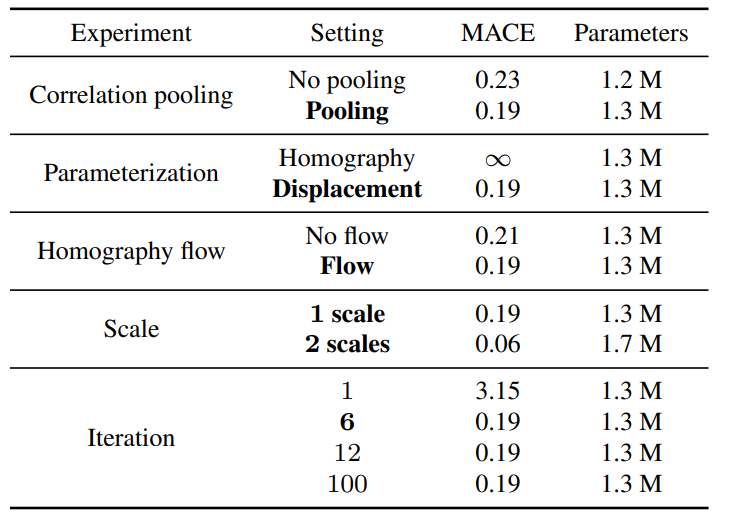
위의 결과를 요약하자면 Correlation Pooling을 수행하고, Homography Flow를 활용하며, 호모그래피를 반복적으로 갱신할 때 displacement 관점으로 접근하였더니 적은 파라미터 상승으로 성능 향상을 일으킬 수 있었다고 말합니다.
게다가 2scale로 진행하였을 때 역시 0.4M 밖에 파라미터가 상승하지 않으면서 성능 향상은 매우 큰 폭으로 상승하는 것을 확인할 수 있었습니다.
또 한가지 재밌는 점은 iteration을 6번까지만 하면 그 이후에는 더 큰 iteration을 반복한다 하더라도 성능 향상이 있지 않았으며 100이라는 매우 큰 횟수의 반복을 할 경우에는 보통 모델의 학습이 잘못된 방향으로 빠질 법한데 그런 현상도 전혀 일어나지 않고 안정적으로 수렴을 했다고 합니다.

위에 그림의 경우 (a)는 정성적 결과를 나타낸 것이며, (b)의 경우 moving obejct를 제거하기 위한 inlier maks의 정성적 결과입니다. 먼저 정렬 결과의 경우에는 초록색 박스가 GT라면 모델은 학습을 통하여 붉은색 박스를 초록색 박스의 shape처럼 변형해서 맞추면 됩니다.
해당 정성적 결과에서 보이는 예시들은 모두 차량이나 자전거를 탄 사람처럼 moving object가 있는 상황이기 때문에 source 영상에서는 없지만 target 영상에서는 존재하는 물체 등 대응관계를 구하는데 있어 방해를 주는 요소들이 있어 학습이 어려운 상황입니다.
이러한 물체들을 제거하기 위한 마스크들이 바로 inlier mask라고 보시면 될 것 같으며 저자는 기존의 mask를 활용한 방법들과 비교하였을 때 자신들이 제안한 방법론의 마스크가 동적인 물체를 잘 인식해서 제거했다고 주장합니다. 음 사실 마스크가 그렇게 뚜렷하지 못해서 무엇을 봐야할지는 모르겠지만, 그래도 차량이 있는 부분이나 보행자가 서있는 영역이 다른 영역에 비해 까맣게 있는 것을 보아 동적인 물체를 올바르게 제거할 수 있다고 보여집니다.

다음은 모델의 추론 시간입니다. 아무래도 전처리에 활용되는 호모그래피 추정 방법론 특성상 처리 속도가 빨라야한다는 것 역시 중요한 고려 대상 중 하나일 것입니다. 1scale IHN의 경우 약 30.6ms로 겨우 33 FPS정도 맞추는 듯 보이며 2scale-mov의 경우 93.6 ms로 11 FPS 정도 나오는 것으로 보아 실시간 처리 속도로는 활용하기가 어려울 듯 보입니다.
하지만 iterative 한 방법론들과 비교하였을 때 상대적으로 매우 빠른 속도에 해당하기 때문에 논문에서도 타 방법론과 비교하여 빠른 추론 속도를 보인다는 식으로 장점을 어필하고 있는 것 같습니다.
결론
iterative 방식으로 호모그래피를 추정하는데 있어 기존의 방법론들은 딥러닝을 온전히 활용하지 못한다는 한계가 있는 반면 해당 방법론은 비교적 깔끔하게 end to end로 잘 활용한 모습입니다. 그래서 좋은 성능도 달성하였구요. 한가지 아쉬운 점은 해당 분야의 아쉬움일 수도 있겠으나 학습 및 평가 데이터의 해상도가 너무 작다는 점입니다. 학습 및 평가가 128×128 패치에서 진행된다는 점에서 640×512 정도의 해상도만 되더라도 모델이 엄청 느린 추론 속도를 가질 것 같아 그 부분이 조금 아쉽게 느껴지네요.
리뷰 잘 읽었습니다.
기존의 iterative한 방식들은 iteration마다 H를 예측해서 warping하는 과정을 수행하기에 warped image를 저장해야하는 메모리가 축적되지만, 본 논문의 방식은 iteration마다 warping을 하는것이 아니라 GMA의 output인 delta(D^^^ k)를 사용해서 offset만을 update하기 때문에 메모리 이슈가 없는 것으로 이해하였는데 맞나요??
그리고 부가적인 부분이긴 한디, 초반부에 계산된 correlation이 너무 커서 average pooling을 수행했는데, 그냥 앞단계인 feature map을 구하는 부분에서 layer를 한번 더 태워도 될 거 같다는 생각이 드는데.. 이에 대한 저자의 언급은 없나요?
음 먼저 첫번째 질문에 대한 대답으로는 물론 논문에서도 update된 offset을 활용해서 warping 작업을 수행하기는 해야합니다. k번째에서 구해진 호모그래피로 warping을 하지 않으면 iteration을 반복한다는 의미가 없기 때문이죠.
하지만 제가 생각했을 때 저자의 방법론이 메모리를 덜 먹는 이유에 대해서 모델의 구성이 그리 무겁지 않고 원본 해상도의 영상을 warping하는 것이 아닌 4배 또는 8배 다운샘플링된 mesh grid를 warping하기 때문이지 않을까 싶습니다.<수정> 해당 논문 말고 그 이전의 방법론들 그림을 살펴보니깐 갑자기 그 차이를 명확하게 알겠더군요. 이전의 iteration 기반 방법론들은 k번째 단계를 예시로 들 때 먼저 k번째 호모그래피를 구해서 source image를 warping하고 k+1번째로 넘기면 해당 단계에서의 또 새로운 네트워크에 태워 k+1번째의 호모그래피를 계산하게 됩니다.
하지만 이번에 리뷰한 논문의 경우는 k번째 안에서 iterative한 방식으로 호모그래피를 추정한 후 필요에 의하면 k+1번째로 넘겨서 한번 더 iterative하게 호모그래피를 구하게 됩니다. 즉 쉽게 말하면 기존의 방법론들은 단일 for문이었다면, 해당 방법론은 2중 for문형식으로 호모그래피를 예측한다는 것이며, 제일 바깥쪽 for문은 매번 새롭게 모델을 학습시켜야만 하지만 안쪽 for문은 하나의 모델을 계속 반복적으로 활용할 수 있기 때문에 iteration의 수가 k개라 하더라도 모델의 수 역시 k개일 필요 없이 1개만 있어도 호모그래피를 추정할 수 있게 됩니다.
그리고 2번째 질문에 대해서는 이 correlation map이 물론 장점도 명확하지만 단점도 명확한 기법입니다. 해상도가 높아지면 연산량이 기하급수적으로 늘어난다는 점이죠. 이러한 관점에서 저자는 feature map 2개에 대해 각각 correlation map을 계산하는 방식보다는 correlation map을 한번 계산하였으면 그 map에다가 avg pooling을 수행하는 것이 연산량을 더 줄일 수 있다고 판단한 것 같습니다.