
안녕하세요. 뭔가 되게 오랜만에 x-review를 작성하는 거 같네요.
오늘 리뷰하게 될 논문은 multi-modal 에서의 Image Registration한 논문입니다.
신정민 연구원과 마무리중인 논문이 Image Registration 분야이기 때문에 본 논문을 읽게 되었습니다.
그럼 리뷰 시작하도록 하겠습니다.
Introduction
본 논문은 multi-modal 에서의 image registration을 수행하는 unsupervised 방법론입니다.
다시말해, domain이 다른 image pairs 에서의 registration을 수행하는 task라고 생각하시면 됩니다.
예를들어, KAIST Dataset같은 경우에 RGB-Thermal image pair 가 두 카메라의 baseline 차이 때문에 align이 맞지 않게 되는데, 이런 경우에 align을 맞출 수 있는 task 입니다.
이전의 Multi-Modal Image Registration task 에서는 source 와 target 사이의 유사성을 최대화하는 방향으로 단순히 source image를 warping 시키는 방식으로 registration을 진행하였습니다.
하지만 source 와 target의 domain이 다르기 때문에,
둘 사이의 유사성을 효과적으로 설계하는 것에는 큰 어려움이 있습니다.
이에 착안을 하여 본 논문에서는 앞선 방식들과 다르게
image translation network와 image registration network 2가지를 동시에 사용하게 됩니다.
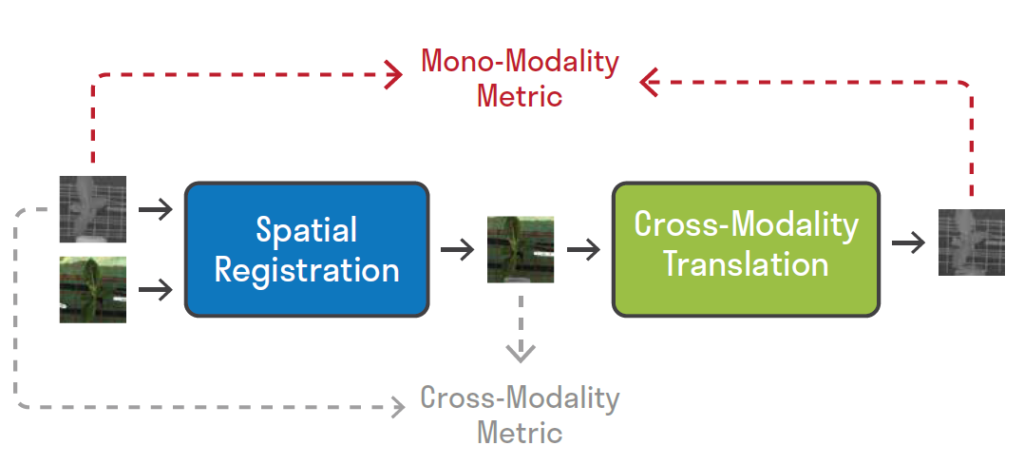
multi-modal image pair에 대해
Registration Network(Spatial Registration, 파랑색) 를 적용해서 registration을 적용해서 align을 맞춰주게 됩니다.
그 뒤, Translation Network(녹색) 를 적용해서 domain을 변경해 주면 결론적으로 source image 와 domain, align이 모두 일치하는 warped image를 얻을 수 있게 됩니다.
domain이 다르다면 위의 회색 화살표로 표시한 Cross-Modality Metric을 사용해야 할겁니다.
domain이 다르므로 Metric 설계도 어렵고, 아무래도 정확도도 떨어지겠죠?
하지만 본 논문은 Translation Network를 사용해서 domain을 변경 해 주었습니다.
이들은 domain이 일치하므로 위에서 빨간 화살표로 표시한 Mono-Modality Metric을 적용할 수 있게 됩니다.
말이 어렵지만 단순 l1 loss라고 생각하시면 됩니다.
기존에 domain이 다른 경우엔 l1 loss를 적용할 수 없지만, domain을 일치시켰기 때문에 Mono-Modality Metric 을 적용시킬 수 있다~ 라고 이해하시면 됩니다.
서론이 너무 길어졌네요,,,
아래에서 마저 설명하겠습니다.
Method
Image Registration을 위한 network는 크게 2가지로 구성됩니다.
1) Spatial Transformation Network(STN) -> R = R_\phi, R_S
2) Image-to-Image Translation Network -> T
하나씩 설명 드리겠습니다.
Registration Network
아래 그림은 둘중 1) 을 나타낸 그림입니다.
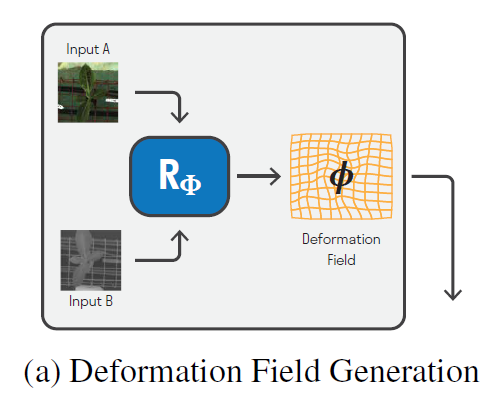
위 모델 그림(a) 에서,
R_\phi 는 multi-modal pairs를 input으로 받고, deformation field \phi 를 생성합니다.
deformation field \phi 란 multi-modal 에서 align이 맞지 않는 이미지의 align을 맞춰주기 위한 변형 matrix라고 생각하시면 됩니다.
\phi = R_\phi(I_a, I_b) 를 통해 2장의 multi-modal input image 사이의 deformation field \phi를 구하게 됩니다.
\phi 는 HxW 로 구성된 2-dimensional 인데, 각 pixel의 변형되는 방향을 나타냅니다.
이를 사용해서, 아래 식을 통해 두 image의 align을 맞추는 Image Registration 과정을 진행하게 됩니다.
여기서 v는 각 pixel v=(i, j) 를 나타냅니다.
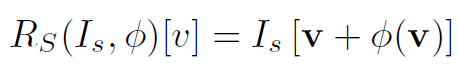
다시 정리하자면,
domain이 다른 두 image I_a와 I_b 가 주어졌을 때, Spatial Transformation Network(STN)인 R_\phi 로 deformation field인 \phi 를 구해서 multi-modal 에서의 registration을 수행할 수 있다~
뭐 이런겁니다.
Geometric Preserving Translation Network
위에서 Image Registration을 위해 deformation field \phi 를 생성했다면,
이번엔 Image Translation에 대한 설명입니다.
위 그림에서 Image-to-Image Translation network인 T는 본 논문의 표현에 의하면
‘geometric preserving‘ 한 상태로 training 되어야 합니다.
이 말은 즉슨, T는 기하학적 이동에는 관여하지 않은 채
오직 domain을 변경하는 photo-metric mapping만 수행하게 되고,
geometric registration task는 앞서 설명드린 R이 독립적으로 수행한다는 뜻입니다.
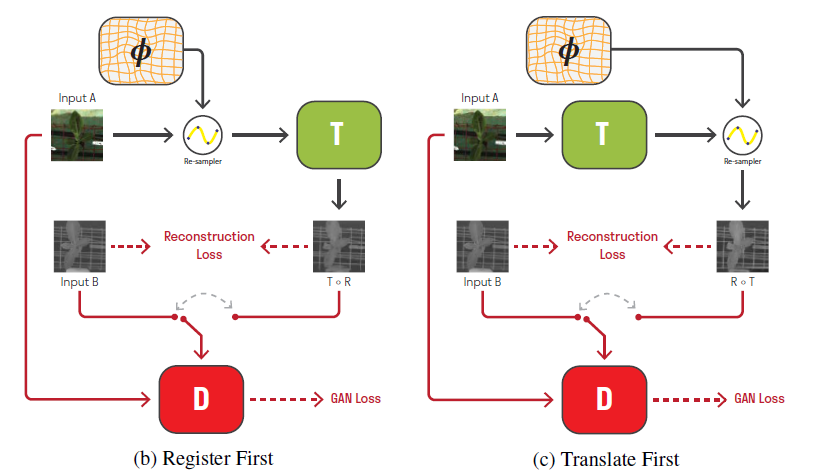
여기서 논문의 저자는 T의 geometric preserving을 유지하고자, T \circ R = R \circ T 라는 식을 설계하게 됩니다.
T \circ R의 경우 Registration을 먼저 적용해서 align을 맞춘 뒤 Translation으로 domain을 맞춰주는, (b) 의 경우에 해당되고, R \circ T 는 순서를 바꾼 것으로 (c) 에 해당됩니다.
각각을 식으로 표현하면 아래와 같습니다.
<Registration First>
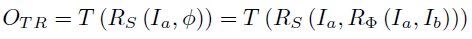
<Translation First>
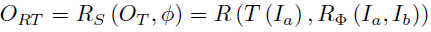
Training Loss
Loss는 총 3가지의 term으로 구성됩니다.
<smooth loss>
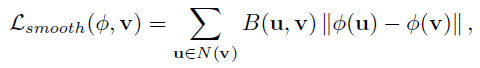
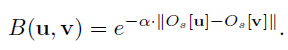
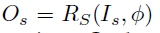
deformation field \phi 로 Registration을 수행하는것과 관련된 loss term 입니다.
위 식에서 || \phi(u) - \phi(v) || 는 인접한 pixel이 유사한 deformation을 가지도록 하는 역할을 합니다.
인접한 pixel끼리 서로 차이가 많이 존재하는 deformation을 수행할 경우 왜곡이 발생할 수도 있으므로, smooth 과정을 통해서 이를 방지 해 줍니다.
여기서 인접한 pixel이란 이웃하는 8개의 pixels를 의미합니다.
B(u,v) 는 over-smoothing을 방지해 주는 bilateral filter라고 소개합니다.
왜곡을 방지하고자 smooth하게 만들기는 해야하지만, 과도한 smooth는 방지하고자 해당 부분을 추가한 것 같습니다.
<reconstruction loss>
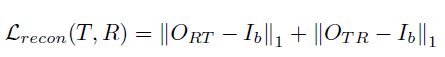
기존 source image인 I_a 가 registration과 translation 과정을 모두 거쳤으므로,
I_b 와 align, domain을 일치시킨 상태입니다.
domain이 일치하므로 논문 상단부에서 설명한 Mono-Modality Metric 을 적용할 수 있습니다.
따라서 단순 photometric loss(L1 reconstruction loss) 를 적용한 것을 볼 수 있습니다.
<cGAN loss>
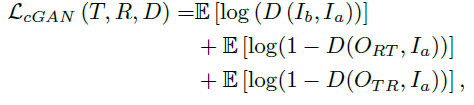
기존 conditional GAN 에서 사용된 loss를 그대로 차용하였습니다.
<<Total loss>>
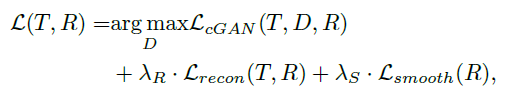
위 3가지 loss를 결합한 total loss는 아래와 같습니다.
Experiment

본 논문에서는 성능 평가를 위해 직접 test set에 대해서 gt를 annotation 했다고 합니다. 위의 그림처럼 말이죠.
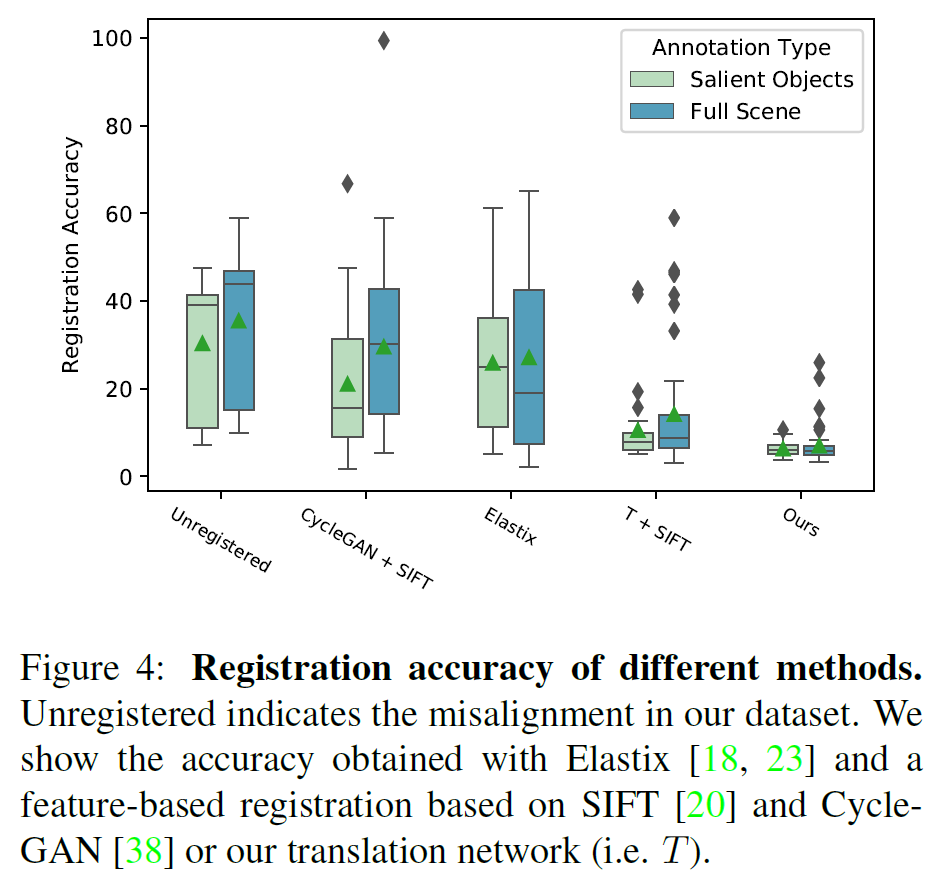
성능은 Image Registration을 진행했을 때의 정확도(accuracy)를 측정하였습니다.
기존 source image와 deformed source image에서 gt matching point pairs의 Euclidean distance의 평균을 측정했습니다.
위의 그래프가 성능의 예시인데, y축이 accuracy여서 높을수록 좋다고 생각을 하실 수 있지만,
사실은 Euclidean Distance를 나타내는 것이므로, 작을수록 성능이 좋은 것입니다.

정성적인 결과는 위와 같습니다.
domain과 align이 서로 맞지않는 이미지 A,B 에 대해 Registration을 수행한 결과를 볼 수 있습니다.

또한 위의 결과는 Image Translation을 수행할 때, Geometric Preserving이 되어야 한다는것과 관련된 정성적 결과입니다.
2번째 column의 T(I_a) 를 보시면 Image Translation을 통해 domain이 변경 되었지만,
Input A와 비교했을때 align은 일치하는, 즉 geometric preserving이 잘된 것을 볼 수 있습니다.
본 논문에서는 domain이 일치하지 않는 image pairs에서의 Image Registration을 수행하기 위해, 억지로 Multi-Modal에서의 similarity를 계산하려고 하지 않고 Image Translation 과정을 추가해서 domain을 일치시키는 과정을 넣은 뒤 같은 domain에서 loss를 비교하는 것이 꽤나 인상깊었습니다. 역시 이런저런 분야의 논문을 많이 읽어야 하는 거 같습니다.
하지만 정성적 결과를 나타낸 dataset이 outdoor dataset처럼 복잡하지 않은, 단순한 dataset에서만 실험이 이루어 졌다는 것이 조금 아쉬운 부분입니다. outdoor dataset에서는 적용이 안되서일까요,,,? 암튼 뭐 그러합니다.
최근 Image 끼리의 변환이나 생성과 관련된 논문작업, 그리고 논문읽기를 진행하고 있는데 꽤나 흥미로운 분야인 거 같습니다. 다음에도 더 좋은 논문으로 찾아오도록 하겠습니다. 감사합니다.
좋은 리뷰 감사합니다.
geometric preserving을 유지하기 위한 뒷 내용들은 잘 설명해주셔서 이해가 갑니다. 그런데 근본적으로 geometric preserving을 유지해야 하는 이유가 무엇인가요?
그리고 서로 다른 도메인을 갖는 이미지들의 align은 보통 어떤 지표를 통해 평가하는지도 궁금합니다.
Image Translation을 진행할 때에 geometric preserving을 해야하는 이유에 대한 질문으로 이해했습니다.
Test time때는 multi-modal에서의 Image Registration을 수행할 때에 Translation 과정 없이 deformation field (phi) 만을 생성해서 Registration을 수행하게 됩니다. 즉 Translation이 관여하지 않는다는 것이지요.
그렇기 때문에 training을 할 때에도 geometric 을 align 하는 부분을 오로지 Registration 에서만 수행해야 하는 것입니다. 이러한 이유 때문에 Translation에서는 geometric preserving이 되어야 하는 것이겠지요.
그리고 multi-modal에서의 registration을 진행한 방법론에서는 통상적으로 normalized cross correlation(NCC) 라고 하는 평가지표를 사용한다고 합니다. 신호처리 분야에서 파생된 것이라고 하는데, 밝기 뿐만 아니라 기하학적인 관계까지 고려해서 유사도를 측정하는 방식이라고 합니다.
안녕하세요 좋은 리뷰 감사합니다
deformation matrix가 수식적으로 어떻게 정의되어 있을까요?
해당 행렬이 다양한 변환에 대해 불변성을 보장하는지 궁금합니다
deformation matrix 에 대한 구체적인 수식은 나타나 있지 않고 있습니다.
저자는 deformation matrix 란 HxW 크기를 가진 2차원의 matrix,
그리고 각 pixel은 deformation을 진행하는 방향(direction) 정보를 담고 있다고 언급하고 있습니다.
그리고 본 논문에서 registration을 진행하는 deformation matrix 는 I_a => I_b 로의 non-rigid 변환을 수행하게 됩니다.