논문 소개
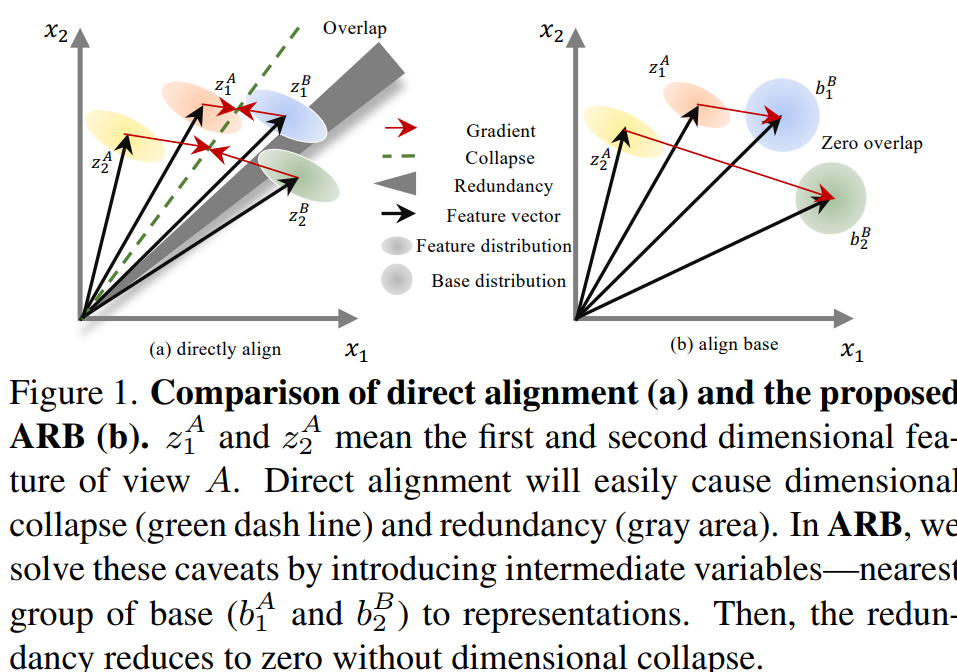
본 논문은 self-supervised learning의 메인스트림중 하나인 contrastive learning에서 발생하는 collapse 문제를 해결하기 위한 논문이다. 인공지능 모델의 학습에서 collapse 현상이란 모델의 출력이 하나의 형태로 수렴하게되는 경우인데, 동일한 contents를 갖는 서로 다른 두 view 이미지(x’, x”)가 같은 값으로 예측된다는 constrastive loss의 쉬운 해결책으로 모든 입력에대해 동일한 output을 생성하도록 모델을 업데이트하는것이 채택될 확률이 높아서 해당 문제가 발생할 수 있다.
collapse 문제를 해결하기 위하여 하나의 view의 예측값을 논문에서 정의한 base 벡터 기반으로 수정하는 일종의 shaping과정을 거친다. 미리 정의한 base 기반으로 예측된 벡터(y’, y”)와 가장 가까운 closest base로 벡터를 변형(y*’, y*”)한다. 이후, cross 하여 두 view의 예측값이 같아지도록 contrastive learning을 진행한다. 즉 기존의 constrastive learning이 (y’,y”) 사이의 거리를 줄이고자 했다면, 제안하는 방법론은 (y’,y*”), (y*’,y”) 사이의 거리를 줄이고자 한다. 비대칭 구조를 설계하여 출력값의 변형해 loss에서 동일한 벡터와 같아지도록 하는 해결책에 가중치를 주는것을 막는다. 또한 이 논문은 이론적인 가정을 수식으로 증명하여 제안 방법론이 왜 self-supervised 방식으로 잘 학습할 수 있는지 증명하였다.
용어 설명
self-supervised learning이란 라벨이 없는 상태에서 인공지능 모델이 데이터에 대해 스스로 학습하기 위한 방법론이다. 일반적으로 어떠한 입력데이터 x에 대해 x가 x이다 라는 정보만 있는 상황에서 학습을 하며, 데이터의 실제 라벨에는 접근 불가능하다는 것이 특징이다. 이를 해결하기 위해 해당 논문에서 사용한 contrastive learning 을 제외하고도 pseudo labeling(=self-training)과 같은 방법론도 있다. constrastive learning은 data augmentation 기법을 이용하여 x의 정보를 최대화 해서 이렇게 많은 x가 모두 x이다 로 문제를 변형하여 해결하고, self-training의 경우 x에 직접 가상의 label을 부여하여 이를 해결한다.
방법론
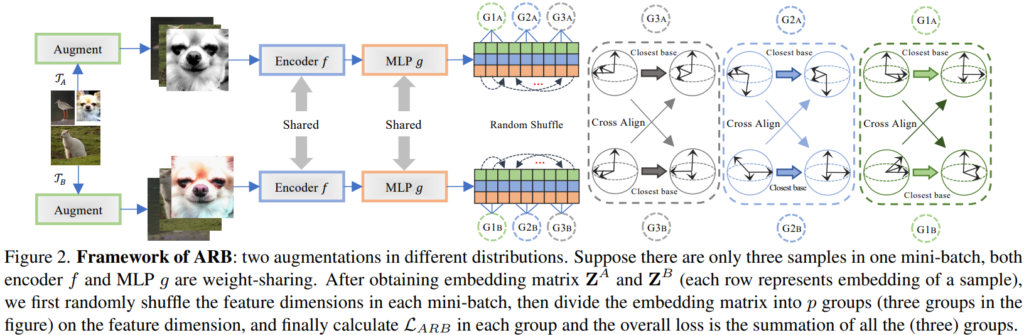
본 논문은 기존 contrastive methods에서 발생하는 collapse문제를 해결하기 위해 basis라는 개념을 도입하여 두 view 중, 하나의 view의 결과를 개선 (basis 표현으로 변환)해 모델이 모든 입력에 대해 하나의 출력값을 갖지 않도록 학습하였다. 논문에서 사용한 basis란 embedding matrix인 z에 대해 가장 가까운 orthonormal metrix를 의미한다. z는 Nxd의 형태(N은 batch size, d는 feature의 차원)를 갖는데, 위의 figure2에서는 N=3인 상황을 의미한다.
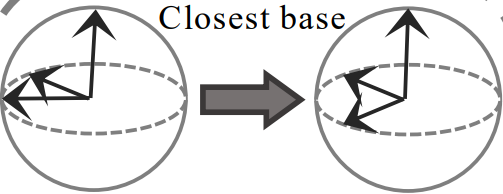
(우) Nearest orthonormal basis (matrix)
어떤 embedding matrix A는 unit vector이며 구에 나타내면 N개의 벡터로 나타낼 수 있다. 해당 unit vector의 조합과 가장 유사한 orthonormal 메트릭스(모든 벡터간의 관계가 수직)가 A의 Nearest Orthonormal Basis(NOB)이다.
마치 비대칭 구조를 통해 collapse를 예방하는 기존 방법론처럼, closest base 변환을 통해 비대칭 구조를 만든다고 이해하면 쉽다. 이때 기존과 다른점은 feature level로 mini-batch 내의 모든 feature간의 관계가 학습에 포함될 수 있다는 점이다. 즉, 기존 방법론의 경우 하나의 context sample에 대한 두 view의 feature 표현이 유사해지도록 학습했다면, 해당 방법론은 N(=mini batch’s size)개의 unit vector 조합을 한번에 학습한다.
입력 X와 X’ (X와 X’은 같은 context를 공유하는 mini-batch set)의 두 embedding 형태를 Z, Z’이라고 하고, 각 embedding 형태의 NOB를 B, B’이라 할 때, 기존 비대칭 구조의 contrastive methods처럼 Z와 B’이 유사해지고, Z’과 B가 유사해지도록 학습한다. 이는 단순히 Z와 Z’이 유사해지게 학습할 때 발생할 수 있는 collapse 문제를 해결할 수 있다. 제안하는 방법론은 이렇게 base 표현형과 유사해지도록 학습하며 논문에서는 Align Representations with Base (ARB)라고 부른다.
직관적 분석
self-supervised learning 분야에서 instance level contrastive learning이 feature level contrastive learning 보다 좋은 성능일 보이는 것은 이미 증명되었다. 그럼에도 feature level의 접근법을 사용한 이유는 다음과 같다.
- 표현 dimension과 mini-batch의 크기. 제안하는 ARB는 주로 d(표현 차원)>=N(batch size) 이기 때문에 instance level을 이용하면 각 sample간의 거리를 고르게 할 수 없다.
- Hard positive. ARB를 적용했을 때 hard positive 가 있으면 두 sample의 표현 벡터는 유사해진다. 이때 feature level 접근법보다 sample level 접근법이 성능에 더 크게 영향을 준다.
위와 같은 분석과 함께 실제로 instance level에 ARB를 적용한 실험의 결과는 아레의 테이블과 같다. 분석과 마찬가지로 feature level에서 더 좋은 성능을 보임을 확인할 수 있다.
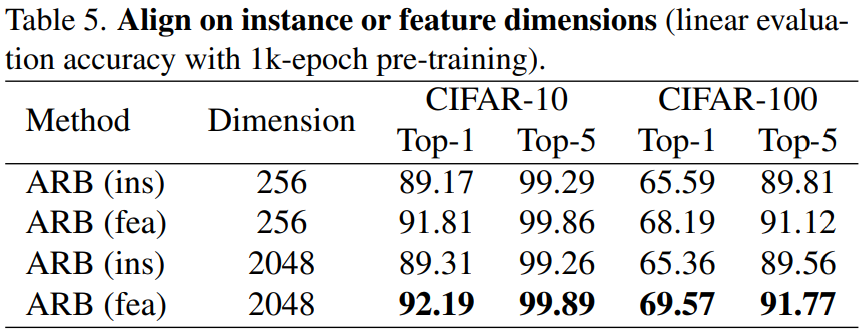
실험
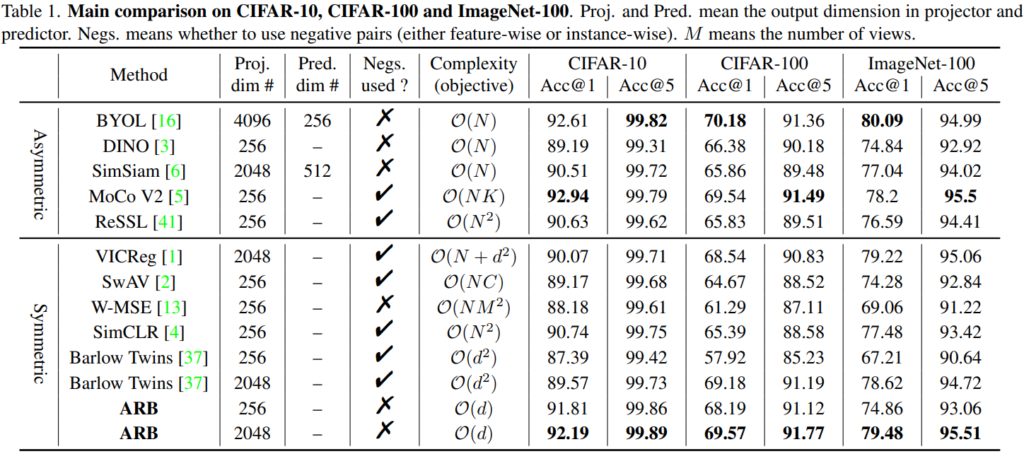
실험은 self-supervised연구 에서 많이 사용하는 CIFAR-10, CIFAR-100, ImageNet-100, ImageNet-1k를 통해 진행하였으며 결과는 아래의 표와 같다. 제안하는 ARB 방법론이 가장 효과적임을 확인할 수 있다.
리뷰 감사합니다. 덕분에 collapse 현상이 어떤 느낌인지 알 수 있었습니다.
질문을 하나 드리자면, 결국 basis vector를 가지고 기존의 embedding vector를 어떻게 변형한다는 것인지 리뷰에 설명이 빠진 것 같아 질문드립니다. orthonormal 얘기가 나오던데 embedding vector를 모아둔 embedding matrix를 직교화 한다는 의미인가요?
직교화 하는것이 맞다면 직교화는 행렬분해를 통해 이뤄지나요? 아니면 레이어를 거쳐서 일어나나요?
감사합니다.