* Intro [go to paper?] *
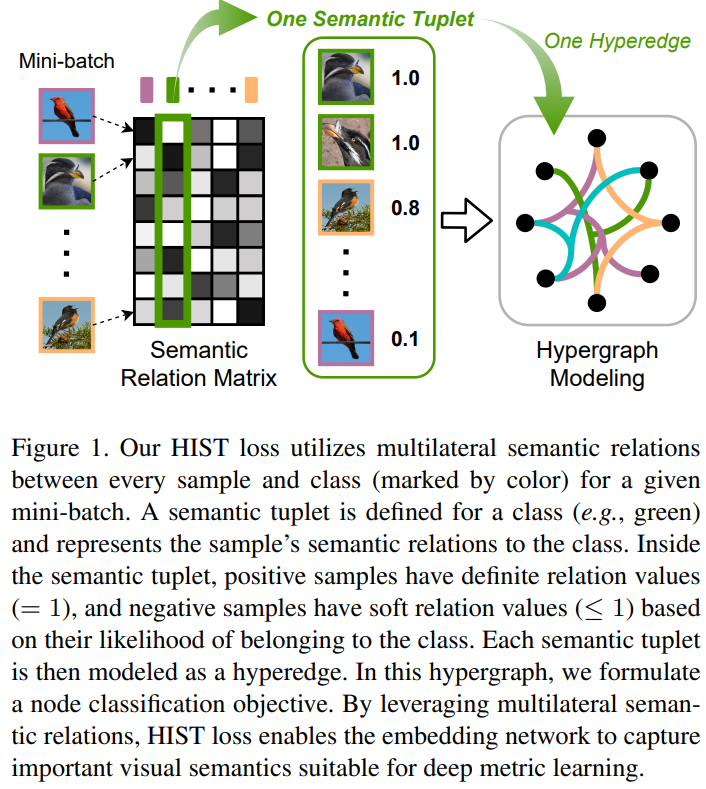
Triplet loss 는 직관적인 metric learning 방법론 중 하나이다. metric learning이란, 데이터간의 유사도를 거리기반으로 표현할 수 있는 인코더 f를 학습시키는 방법론인데, Triplet Loss로 대표할 수 있는 pair-based loss, semantic 정보를 캡쳐하기 위해 sample기반의 pair가 아닌 sample들의 대표인 proxy를 이용하는 proxy-based loss, 마지막으로 semantic 정보에 가장 초점을 맞춘 classification based loss 등으로 학습된다. 각 방법론은 data instance에 초점을 맞추거나 sematic information에 초점을 맞추는 두가지 선택지중 하나를 따르는데, data instance 에 초점을 맞춘 pair-based loss는 학습과정 중 semantic 정보에 대한 캡쳐가 어렵고 수렴이 느리다는 단점이 있다. 또한 proxy-based 혹은 classification-based 와 같이 semantic level information에만 치중하면 sample간의 관계를 통해 얻을 수 있는 디테일한 지식들을 학습하지 못할 위험이 있다. 이러한 기존 방법론에서의 단점을 보안하기 위해 본 논문은 semantic information과 instance level information 모두를 학습할 수 있는 graph 기반의 tuple loss를 제안한다. 제안하는 HypergraphInduced Semantic Tuple(HIST) loss의 개괄은 [그림1]에서 확인할 수 있다.
* Existing metric learning work *
Pair-based loss. 데이터간의 차이와 공통점을 모델이 직접 캡쳐하도록 기준이 되는 anchor data에 대해 positive pair와 negative pair를 구성하여 positive pair와는 가까워지도록, negative pair와는 멀어지도록 하는 학습법이다. 데이터에 대한 semantic label이 없어도 pair를 구성할 수 있다는 것(positive는 자기자신, negative는 다른 instance data)이 장점이다. 그러나 수렴속도가 느리며 학습의 자유도가 높기때문에 pair를 잘 구성하지 못하면 학습이 어려울 수 있다. 방법론의 예시로는 Triplet loss, N-pair, Lifted Structure, Tuple Margin loss 등이 있다.
Proxy-based loss. pair 기반의 방법론은 instance 간의 관계를 이용하는 만큼(pair간의 관계성이 다양하기 때문에) 학습이 불안정하다. 이에 대한 해결책 중 하나는 sample간의 관계가 아닌 데이터의 대표간의 관계를 비교하는 proxy-based 방법론이다. 해당 방법론의 예시로는 ProxyNCA, Manifold Proxy, ProxyNCA++ 등이 있다. 그러나 앞서 언급하였듯이 데이터의 대표만을 metric loss에 이용하므로써 sample을 통해 학습할 수 있는 디테일한 특징 정보를 캡쳐하지 못한다.
Classification-based loss. 앞선 proxy 기반의 방법론보다 더욱 sematic level에 다가간 학습방식으로, (일반적으로) 모델 학습자가 직접 지정한 카테고리를 이용하여, 해당 카테고리에 속하는 다양한 데이터 샘플을 통해 카테고리의 특징을 학습하도록 하는 방법론이다. 해당 방법론은 매우 일반적이고 유명하며, 그 예시로는 Normalized Softmax, SoftTriple 등이 있다. 해당 방법론 역시 proxy-based loss와 같이 sample간의 관계를 통해 학습할 수 있는 디테일을 캡쳐하기 어렵다는 한계가 있다.
Graph-based loss. graph-based 학습법은 데이터간의 관계를 학습하기에 좋은 방법론이다. 해당 방법론에 속하는 연구인 group loss는 mini-batch 안에 있는 모든 샘플을 통해 Label propagation(LP) 방식을 활용하여 거리표현을 학습한다. Label propagation(LP)[wiki]란 latent space에서 labeled data의 가까이에 있는 unlabeled 로 label을 전파시키므로써 unlabeled data에 레이블을 부여하는 방법론으로, graph-based 학습법에서 많이 이용한다. group loss 외에도 proxyGML, IBC 등 다양한 관련 연구들이 mini-batch 단위로 구성한 그래프에 LP 방식을 이용하여 표현학습을 진행한다. 이러한 graph 기반의 방법론의 학습과정은 datasample간의 pairwise relations에 치중되는데 node와 node간의 관계를 통해 학습하기 때문이다. (보통 node가 하나의 instance sample이 된다.) 이에 반해 논문에서 사용하는 hypergraph는 데이터간의 higher-order relations을 캡쳐할 수 있는데, 여러 노드를 연결한 hyperedge가 이를 가능하게 한다.
* Method *
* 본 논문의 제안인 HypergraphInduced Semantic Tuple(HIST) loss의 목적은 데이터의 semantic level information과 instance level information을 동시에 캡쳐할 수 있음에 있다. *
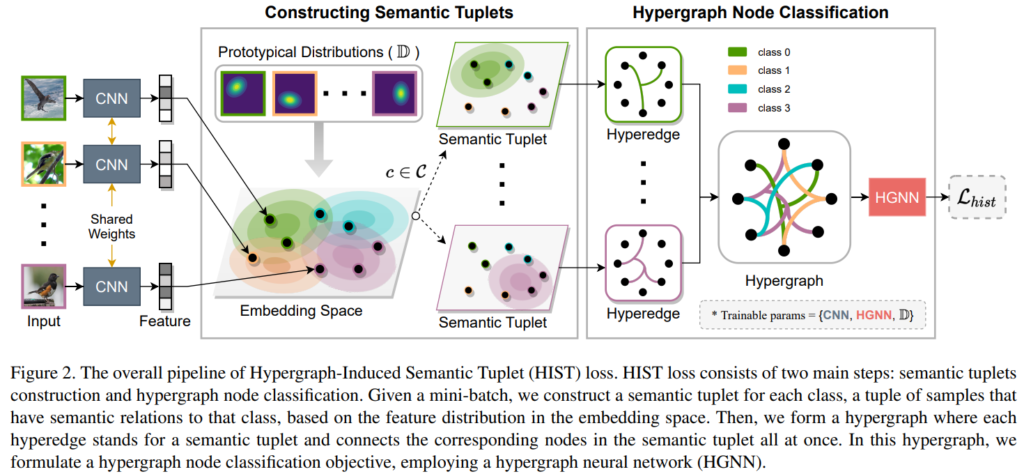
제안하는 방법론은 [그림2]의 방식으로 구현되었다. graph 구조를 이용하여 sample간의 관계에 대한 학습을 가능하게 하고, prototypical distributions을 정의하여 semantic level information도 학습할 수 있도록 하였다. 전체 학습 loss는 prototypical distributions를 학습하기 위한 loss와 cross-entropy loss로 구현된 L_hist loss이다. sample간의 관계는 여느 graph 기반의 방법론같이 mini-batch 단위로 학습한다. 간단하게 이해하자면, 기존 방법론은 graph 기반으로 sample간의 관계를 통해 유사한 데이터는 유사한 공간으로 임베딩되는 representation 함수를 학습하지만, 제안하는 방법론은 prototypical distributions 을 정의해 사용하여, 같은 semantic label을 갖는 데이터를 미리 지정한 공간에 임베딩 되도록 학습하여 sematic 정보를 강화하고, 특히 여러 노드(=data sample)간의 관계를 캡쳐할 수 있는 hyperedge 구조를 사용하여 representation 함수가 sample간의 관계와(low-level), high-order relation을 모두 학습할 수 있도록 한다.
Prototypical Distributions. 제안하는 방법론은 학습가능한 분포집합인 prototypical distributions를 이용해 데이터의 embeding space를 학습한다. 기존 classification 방법론의 경우 같은 semantic information을 갖는 다양한 데이터를 하나의 label로 예측되도록 학습한다. 그러나 각 sample간의 intra-class variations은 다양하며, 이는 카테고리마다 다르다. 이러한 경향성을 반영해 논문은 데이터들의 평균(µ, class centroid를 의미)와 공분산(Q, 2개의 확률변수의 선형 관계를 나타내는 값, intra-class variations을 의미)를 학습한 prototypical distributions를 정의하였다. 이 과정에서 연산효율성을 높이기 위해 공분산이 대각행렬이 되도록 했다. 각 prototypical distribution 의 갯수는 카테고리 갯수와 같다. prototypical distribution의 학습 loss는 sample z_i가 올바른 prototypical distribution인 D_+에 할당 될 확률을 의미하는 p_i가 최대가 되도록 학습하며 그 loss 는 [수식1]과 같다. [수식 1]에서 i는 mini-batch에 속하는 instance number, dm은 squared mahalanobis distance 계산함수이다.
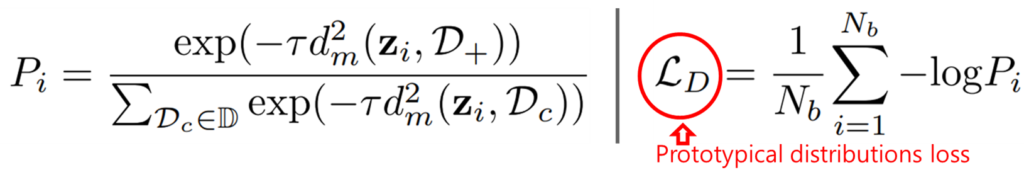
Hypergraph modeling. prototypical distributions을 따르도록 잘 학습된 feature를 통해 hypergraph를 생성하기 위해서는 먼저 노드간의 hyperedge를 구성하기 위해 Semantic Tuplets을 구성해야한다([그림2] 참조). Semantic Tuplets은 각 카테고리에 속하는 mini-batch내 학습데이터의 조합으로 구성되며 카테고리마다 하나의 메트릭스로 선언된다. Semantic Tuplets의 정의는 [수식2]와 같으며 j는 class number, i는 mini-batch에 속하는 instance number이다. 수식에서 d는 거리 계산 함수인 squared mahalanobis distance이며 α는 상수이다.
또한, 그래프는 [수식3]과 같이 정의되는데, class number 개수(j)만큼의 열과 데이터 개수(i)만큼의 행을 갖는 행렬 H_ij로 정의된다.([그림1]참조) 각 node는 mini-batch의 각 sample을 의미하며 hyperedge는 앞전에 구성한 semantic-tuple를 통해 생성한다. 이때 각 노드간의 관계는 weight를 갖는데 positive hyperedge(같은 카테고리에 속하는 데이터일 경우)는 1, 그렇지 않을 경우는 negative hyperedge로 하여 1보다 작은 양수로 가중치를 갖는다. 이를 통해 같은 공간으로 배정됬지만 실제로 negative인 hard negative sample(=hard negative node)와의 거리를 벌림으로써 더 좋은 표현력을 갖을 수 있다.
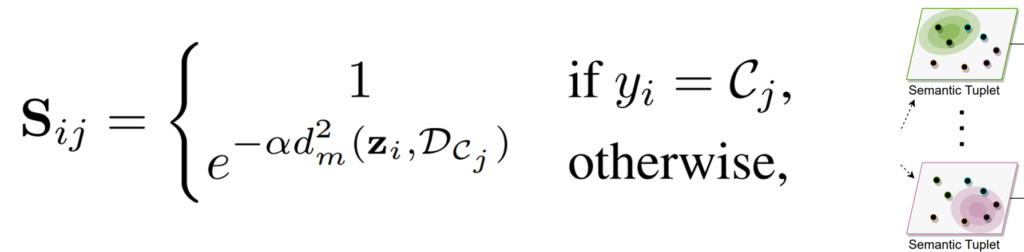
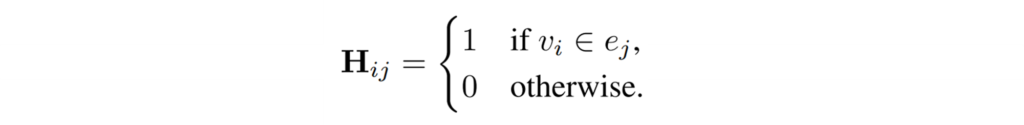
HIST Loss. 이렇게 hypergraph를 구성하고 나서, 기존 방법론(HGNN, Hypergraph Neural Network)에서 사용했던 Hypergraph message passing steps을 거친다. 이는 노드간의 관계를 이용해 네트워크를 학습시키는 graph 기반 방법론의 네트워크 방법론으로 l번의 반복학습을 거친다. message passing 기반의 네트워크 업데이트가 끝난 후, softmax 함수를 통해 class를 예측하고 그 정확도를 향상시키기위한 loss를 추가하여 semantic level의 information에 대한 표현력을 강화시킨다. 따라서 제안하는 L_hist 는 [수식4]와 같다.

* Experiments *
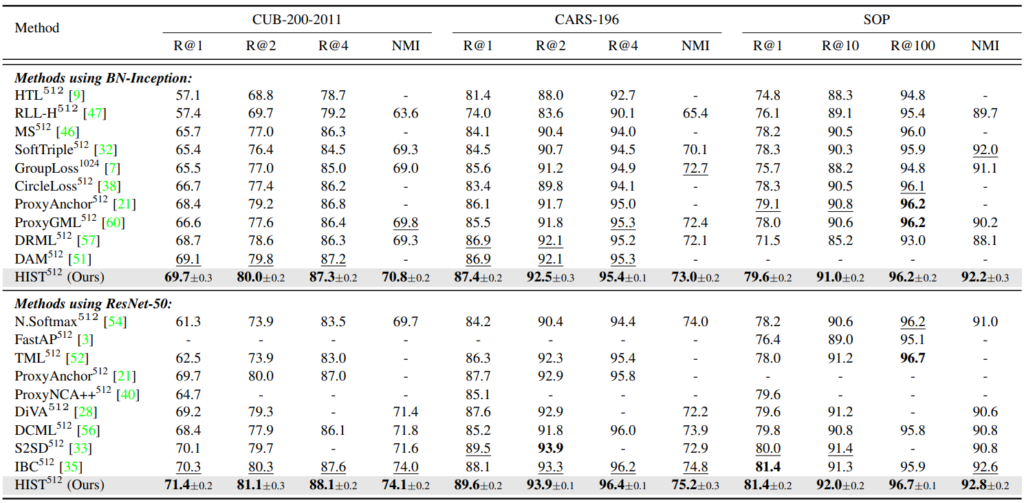
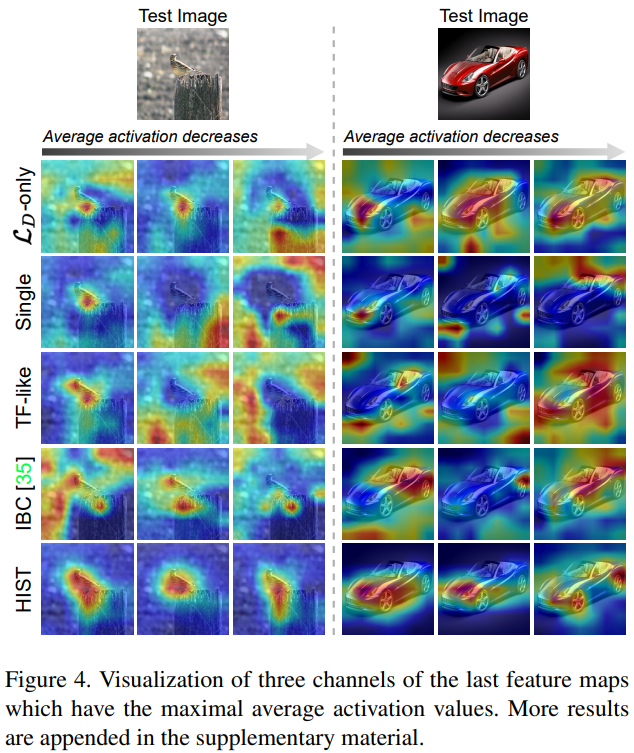
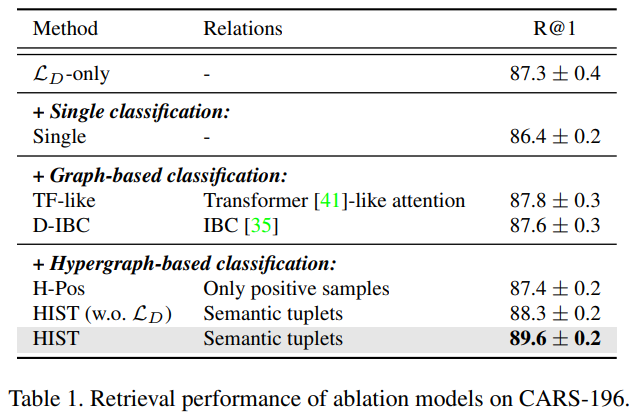
실험은 deep metric learning 방법론간의 비교를 위해 자주 사용되는 데이터셋 세가지(CUB-200-2011, CARS-196, Stanford Online Products(SOP))를 통해 진행되었다. 실험결과로는 parameter analysis, self-evaluation[그림5], comparison with state-of-the-arts[그림3, 4] 를 제공한다. [그림3]에서 알 수 있듯이 기존 방법론에 비해 좋은 분류성능을 보임으로써 제안하는 방법론의 학습이 좋은 feature 표현법을 학습함을 알 수 있다. 또한 [그림4]와 같은 정성적 결과를 통해 제안하는 방법론으로 학습한 모델이 이미지에서 forgroud 물체에 잘 집중하고 있음을 보였다. [그림5]는 self-evaluation을 보이는 실험 중 하나인데, sample간의 관계에 치중된 graph 기반 방법론과 sematic level information 에만 집중하는 classification 방법론보다 제안하는 방법론이 좋은 표현력을 가짐을 실험을 통해 보였다.