Before Review
이번 논문도 Weakly Supervised Temporal Action Localization으로 읽었습니다.
인상 깊은 점은 논문의 아이디어가 전통적인 머신러닝 기법에서 기인한다는 점입니다. 덕분에 이번 논문을 읽으면서 GMM(Gaussian Mixture Model)이 무엇인지도 제대로 알게 된 것 같습니다.
그럼 리뷰 시작하도록 하겠습니다.
Preliminaries
본 논문을 이해하기 위해서는 Gaussian Mixture Model이 무엇이고 이것의 파라미터를 추정하는 알고리즘 중 하나인 Expectation Maximization을 알아야합니다. 내용이 깊게 들어가면 어려운데 본 논문을 이해하기 위한 정도로만 설명하도록 하겠습니다.
Gaussian Mixture Model
우선 가우시안 혼합 모델이라 불리는 수학적 테크닉에 대해서 알아보도록 하겠습니다. 예를 들어 아래와 같은 데이터의 분포가 있다고 생각해보겠습니다.

왼쪽 사진을 보면 전체 데이터의 분포를 하나의 가우시안 분포로 근사하여 설명하고 있습니다. 그래서 그런지 전체 데이터를 완전하게 설명하기에는 조금 부족해보입니다. 가우시안 분포 중앙 부분에는 실제로 데이터가 별로 없기 때문입니다.
오른쪽 사진을 보면 전체 데이터의 분포를 두개의 가우시안 분포로 근사하여 설명하고 있습니다. 앞서서 하나의 분포로만 설명한 것에 비해 이번에는 데이터 분포를 그럭저럭 잘 설명할 수 있을 것 같습니다.
이렇듯 가우시안 분포 등의 기본적인 분포들의 선형 결합으로 만들어지는 확률 모델들을 혼합 분포(Mixture Distributuin), 혼합 모델(Mixture Model)이라 합니다. 가우시안 분포를 가지고 선형 결합을 하면 가우시안 혼합 모델이 되는 것이죠.
충분히 많은 숫자의 가우시안 분포를 사용하고 각 분포들의 평균과 공분산 선형 결합의 계수들을 조절하면 거의 모든 연속 밀도를 임의의 정확도로 근사하는 것이 가능합니다.

이런식으로 말이죠. 결국 어떤 데이터의 분포이든 가우시안 분포를 통해 근사를 시킬 수 있다는 것 입니다.
- p(x)=\sum^{K}_{k=1} \pi_{k} N(x|\mu_{k} ,\sum\nolimits_{k} )
위의 수식은 x라는 데이터에 대한 확률 밀도를 정의한 것입니다. K개의 가우시안 밀도의 중첩이라 볼 수 있죠.
여기서는 3가지의 파라미터를 추정해야 하는데 그것들은 아래와 같습니다.
- 혼합 계수 (\pi_{k}) : 임의의 k번째 가우시안 분포이 선택될 확률 입니다.
- 평균 (\mu_{k}) : 임의의 k번째 가우시안 분포의 평균을 의미합니다.
- 공분산 (\sum\nolimits_{k}) : 임의의 k번째 가우시안 분포의 공분산을 의미합니다.
그래서 GMM(Gaussian Mixture Model)을 fitting 시킨다는 것은 주어진 데이터 분포 X=[x_{1},x_{2},\ldots ,x_{n}]에 대해서 최적의 파라미터 \pi_{k}, \mu_{k}, \sum\nolimits_{k}를 찾는 것과 동일합니다.
Expectation Maximization
위의 매개변수를 찾는 방법은 최대 가능도 방법도 있지만 상황이 조금 복잡해진다고 합니다. 그래서 또 다른 강력한 알고리즘인 기댓값 최대화라는 알고리즘에 대해서 간단하게만 알아보도록 하겠습니다.
우선 다시 가우시안 혼합 밀도에 대한 수식을 살펴보도록 하겠습니다.
- p(x)=\sum^{K}_{k=1} \pi_{k} N(x|\mu_{k} ,\sum\nolimits_{k} )
여기서 \pi_{k}=p(k)는 k번째 가우시안을 뽑을 사전 확률(p(x))로 볼 수 있고 확률 밀도인 NN(x|\mu_{k} ,\sum\nolimits_{k} )=p(x|k)는 k번째 가우시안이 주어졌을 때 x 라는 데이터가 가지는 확률로 볼 수 있습니다.
즉 이렇게 정리할 수 있다는 것이죠.
- p(x)=\sum^{K}_{k=1} \pi_{k} N(x|\mu_{k} ,\sum\nolimits_{k} )=\sum^{K}_{k=1} p(k)p(x|k)
여기서 베이지안 정리(Bayesian’s Rule)를 이용해서 구할 수 있는 사후 확률(p(k|x))을 우리는 책임값(responsibility)라고 정의합니다. 관점을 바꿔서 x라는 데이터 샘플이 주어졌을 때 K번째 가우시안일 확률을 찾고자 하는 것이죠.
이제 책임감(responsibility)이 무엇인지 알아보았으니 알고리즘에 대해서 설명하도록 하겠습니다. Expectation Maximization은 크게 두단계로 나누어져 있습니다. E단계와 M단계이죠.
먼저, 현재의 평균(\mu_{k}), 공분산(\sum\nolimits_{k}), 혼합 계수(\pi_{k})를 초기화 하고 log-likelihood function을 계산합니다.
현재의 매개변수값들을 바탕으로 책임값(Responsibility)를 계산합니다. 이 단계를 E(Expectation)단계라고 합니다.
- p(k|x)=r(z_{nk})=\frac{\pi_{k} N\left( x_{n}|\mu_{k} ,\sum\nolimits_{k} \right) }{\sum^{K}_{j=1} \pi_{j} N\left( x_{n}|\mu_{j} ,\sum\nolimits_{j} \right)}
그리고 추정한 책임감(responsibility)을 가지고 다시 파라미터를 재추정합니다. 이를 M(Maximization)단계라고 합니다. 이 과정에서는 미분이 들어가기도 하고 라그랑주 승수법이 들어가기도 하는데 이번 글에서는 자세히 다루지 않겠습니다.
E단계와 M단계를 통해서 결국 log-likelihood function을 최대화 하는 방향으로 파라미터들이(\pi_{k}, \mu_{k}, \sum\nolimits_{k}) 추정이 됩니다. 최대 가능도 추정의 과정이라 보면 됩니다.
본 논문에서도 E단계와 M단계를 통해서 학습을 시키는 framework를 제안하였습니다. 물론 파라미터를 업데이트 하는 과정에서는 복잡한 미분이나 제약이 들어가지는 않지만 위의 Expectation Maximization의 알고리즘의 전체적인 flow를 따랐다고 볼 수 있습니다.
일단 서론이 너무 길어진 것 같으니 이제 리뷰 시작하도록 하겠습니다.
Introduction
Weakly Supervised Temporal Action Localization(이하 W-TAL)은 Video-level의 라벨만을 가지고 학습을 진행하기 때문에 Classification으로 Localization을 해결한다고 볼 수 있습니다.
Classification으로 Localization을 해결하기 때문에 기존의 방식들은 sub-optimal한 경우가 많았고, 사실 이는 아직도 어려운 부분이긴 합니다. 여러가지 방법이 있지만 가장 간단하게 생각해볼 수 있는 것은 역시 Localization은 Regression 문제로 해결하는 것이겠죠.
하지만 우리가 알고 있는 Label 정보는 Video-level Category 정보 밖에 없기 때문에 최근들어 Pseudo Label을 활용하여 이 gap을 채우려는 시도들이 많았습니다. 비교적 높은 신뢰도를 가지는 구간 예측값에 대해서 Pseudo proposal 만들어서 regression loss를 학습 과정에 포함시키는 것이라 볼 수 있습니다.
이에 저자는 Pseudo label을 만드는 과정에서 중요한 것은 Contextual 한 정보를 이용해야 한다는 것입니다. 비디오의 전체 맥락을 이해해야 한다는 것입니다. 좀 더 정확히 말하면 비디오 전체의 맥락을 이용해야 한다고 표현하는 것이 더 적합할 것 같습니다. 아래의 사진을 통해 무슨 말이지 살펴보도록 하겠습니다.
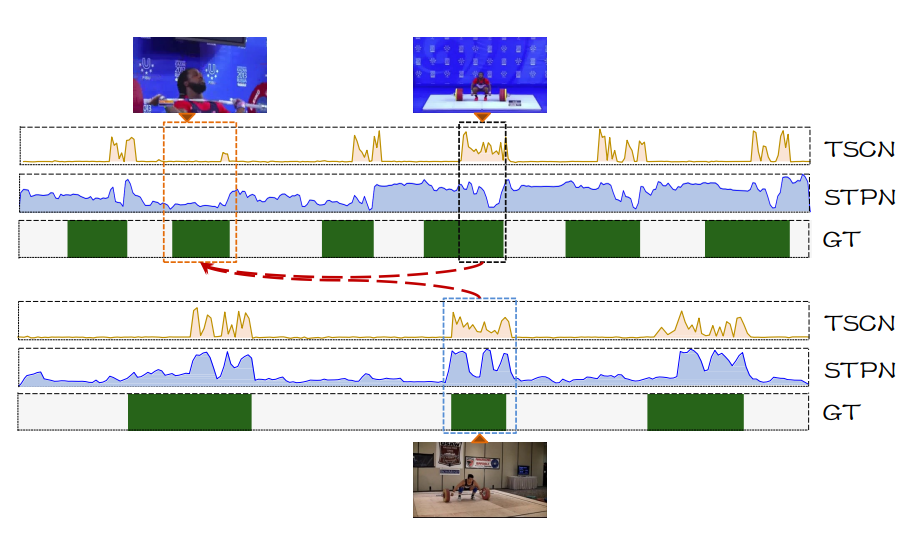
역도를 하고 있는 동영상 입니다. 역도를 하고 있는 전신이 나타나고 있는 부분은 이전 방법론(TSCN, STPN) 가릴 것 없이 score 가 높게 발생하고 있습니다. score가 높게 발생하고 있다면 후에 proposal에 포함될 확률이 올라가기 때문에 구간을 잘 예측하는 데 도움이 됩니다.
하지만 주황색으로 칠해진 부분을 보면 역도를 하고 있는 선수의 상반신만 나타나고 있습니다. 이 부분은 이전 방법론(TSCN, STPN) 가릴 것 없이 score가 낮게 발생하고 있습니다.
저자는 이렇게 맞추기 어려운 부분에 대한 예측을 수행할 때 비교적 비디오 전체를 설명할 수 있는(context information)를 추가적으로 이용해서 보충하면 좋지 않을 까라는 생각을 가지고 본 논문을 제안하게 됩니다.
예를 들어 비디오를 봤을 때 이 비디오의 가장 representative information이 역도 들기라면 저렇게 애매한 부분 역시 역도 들기라고 볼 수 있지 않을까 라는 것이죠.
하지만 여기서 문제가 발생합니다.
- 어떻게 비디오의 전체 맥락을 설명할 수 있는, 가장 뚜렷한 정보를 담고 있는 representative snippet을 얻을 것인가?
- 그 representative snippet이 담고 있는 정보를 어떻게 활용할 것인가?
이에 저자는 Expectation Maximization 알고리즘을 활용한 attention을 활용하여 representative snippet을 추출하고, bipartite random walk module(BiRW)을 통해 representative snippet들의 information을 propagation 시킵니다.
서론은 이쯤으로 마무리하고 이제 방법론에 대해서 알아보도록 하겠습니다.
Proposed Method
Feature Extraction & Classification Head
이 부분은 워낙 이전 리뷰에서도 다룬적이 많고, 모두 거의 동일한 세팅으로 하기 때문에 간단하게만 짚고 넘어가겠습니다. Feature Extraction은 I3D Backbone-network를 통해 고정된 길이의 Snippet에 대한 feature를 사용합니다. Classification Head는 본 논문 저자의 이전 논문인 FAC-Net(2021, CVPR)이라고 하는 베이스라인을 가져왔습니다. 조금 디테일하게 들어가면 원래 구조에서 classwise foreground attention module을 제거했고, softmax 대신 sigmoid를 사용했다고 합니다. 이런 부분은 마이너한 부분이기 때문에 이정도로만 설명하고 본 논문의 메인 아이디어로 넘어가도록 하겠습니다.
Representative Snippet Summarization
우선, 가장 간단하게 Representative Snippet을 얻는 방법은 가장 score가 높은 top-k개의 snippet을 사용하는 것 입니다. 그런데 단순히 score가 높은 top-k개의 snippet feature를 representative feature로 사용했을 때 문제점이 발생합니다. 아래의 그래프를 보면
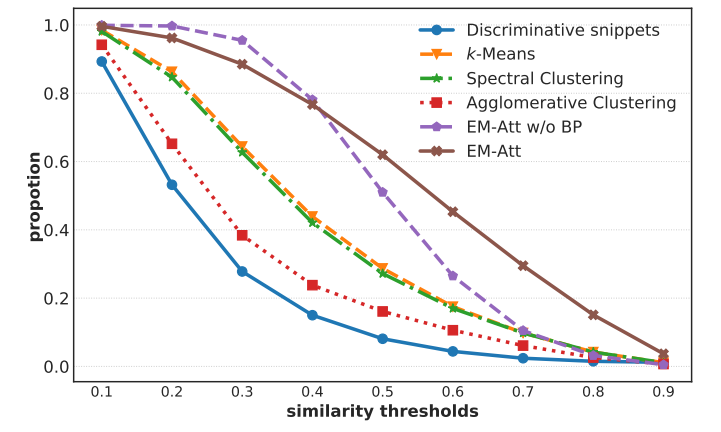
파란색으로 표현된(Discriminative snippets) 그래프가 top-k snippet을 활용했을 때 입니다. Simiarity threshold는 다른 snippet들과의 유사도가 어느정도 나오는지 일정 임계치를 넘어서는 snippet 갯수의 비율입니다. 무슨 소리냐면 similarity threshold가 높은 상태에서 비율이 높다는 것은 representative snippet이 다른 snippet가 유사도가 웬만하면 비슷한 것으로 비디오 전체를 설명하는 가장 대표적인 snippet이라 볼 수 있다는 것입니다.
그래프를 통해 우리는 Clustering 기반의 방법론이 비교적 표현력이 좋은 representative snippet을 얻을 수 있다는 것을 알 수 있습니다. Cluster의 Center들을 representative snippet으로 정의하겠다는 것입니다. 저자는 여기서 Gaussian Mixture Model을 통한 Representative snippet summarization을 제안합니다.
Gaussian Mixture Model(GMM)은 3가지의 파라미터를 추정해야 한다고 앞서 설명했습니다. 공분산은 여기서 identity matrix로 대체한다고 하니 신경쓰지 않도록 하고, 가우시안 분포의 혼합 계수와 각 분포의 평균을 구해야 합니다.
- \mu \in R^{n\times d} : mean 입니다. 하지만 동시에 representative snippet feature 이기도 합니다.
무슨 소리냐면 n개의 가우시안 분포의 통계치를 추정할 것인데 여기서 평균에 해당하는 통계치는 분포를 대표하는 정보이기 때문에 representative snippet이라 볼 수 있다는 것이죠.
- Z\in R^{l\times n} : 혼합계수입니다. Video Feature F\in R^{l\times d}가 있을 때 여기서 l은 snippet의 갯수이고(비디오의 전체 길이), d는 snippet feature의 차원입니다. 여기서 비디오의 구간인 temporal axis에 대해서 혼합계수 Z\in R^{l\times n}를 가지고 weight sum을 통해 representative snippet을 만들어줍니다.
아직까지 뭔가 어지러우니 다시 수식으로 차근차근 정리하겠습니다. 일단 전체적인 흐름은 Expectation Maximization의 형태를 가지고 있습니다. 먼저 E 단계 부터 알아보도록 하겠습니다.
E 단계에서는 현재의 파라미터를 가지고 responsibility를 추정한다고 위에서 설명했습니다. responsibilty를 추정하는 것은 사실 혼합계수를 추정하는 것과 동일합니다. 여기서도 혼합계수인 Z\in R^{l\times n}를 아래와 같은 과정으로 추정합니다.
- Z^{(t)}=softmax\left(\lambda Norm_{2}(F)Norm_{2}\left( \mu^{\left( t-1\right) } \right)^{T} \right)
참고로 \mu \in R^{n\times 0}는 랜덤으로 초기화된 것을 사용합니다.
그 다음은 M 단계입니다. responsibility를 가지고 다시 평균을 추정해줍니다. 그리고 학습은 E-M 단계로 번갈아가면서 점점 평균이 대표성을 가질 수 있도록 학습이 진행됩니다.
- \mu^{(t)} =Norm_{1}(Z^{(t)})^{T}F
사실 이 과정은 결국 비디오 feature F의 weighted sum을 위한 계수를 찾아주는 과정이라 볼 수 있습니다. weighted sum을 통해 representative snippet feature를 얻는 과정이죠.
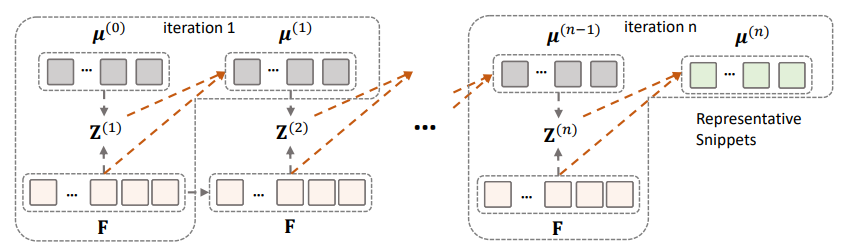
위의 E-M 단계를 반복적으로 거치는 과정을 그림으로 보여주고 있습니다. 각 Iteration 마다 Representative Snippet들이 Update 되는 것을 볼 수 있습니다. 이 과정에서 결국 학습이 되는 것은 무엇일까요? 학습이 되는 것은 Z\in R^{l\times n}인 혼합계수입니다.
원래 Expectation Maximization attention이 처음 제안된 논문에서는 update 과정에서 gradient vanishing 문제 때문에 moving average 방식을 사용했는데 본 논문에서는 일반적인 역전파를 이용하여 update를 했다고 합니다.
이 부분은 실험적인 부분이긴 하지만 결론적으로 역전파를 사용하여 혼합계수를 학습해주는 것이 성능적으로는 더 좋게 나왔다고 하네요.
남은 내용이 Representative Snippet Memory Bank를 구축하는 것과 Snippet Propagation을 어떻게 수행할지가 남아있는데 내용이 조금 어렵기도 하고 본 리뷰도 조금 길어진 감이 있어 남은 내용은 다음 X-Review에서 마저 다루도록 하겠습니다.
감사합니다.