이번에 들고온 논문은 앵커 프리 기반의 물체 검출 알고리즘 논문입니다. 처음으로 앵커 프리를 제안한 논문이며, 수 많은 default boxes를 가진 앵커 기반의 물체 검출이 가진 한계를 어느 정도 극복한다는 점에서 높은 가치가 있는 논문입니다. 또한, 앵커 기반은 GT간 높은 IoU 가진 sample을 positive sample를 추려내어 학습을 진행합니다. IoU를 이용하여 샘플링을 진행할 경우에 IoU의 특성상, small object에서는 상대적으로 낮은 스코어를 보이는 특징이 있습니다. 이러한 이유로 기존 앵커 기반에서는 small object에서는 낮은 성능을 보여주는 결과를 보여줍니다. 반면에 앵커 프리는 다른 방식을 이용하기에 small object에서 좋은 결과를 보여줍니다. 자세한 본문에서 다루도록 하겠습니다.
Intro
기존에 저희가 잘 알고 있는 1 스테이지 기반인 SSD, YOLO와 2 스테이지 기반의 Faster R-CNN 등과 같은 앵커 기반의 방법론은 default boxes를 사전에 정의해야합니다. 정의된 default boxes는 각 픽셀에서의 default boxes * (bbox + num of classes)를 예측합니다.
SSD인 경우에는 하나의 영상에서 8732개의 boxes에 대한 예측 결과가 추론되어집니다. 8732개의 boxes에는 대부분 정답인 아닌 케이스로 구성되어지기 때문에 앵커 기반은 불균형 문제로 많은 문제가 발생합니다. 그렇기에 대부분의 방법론에서는 GT 간의 IoU를 이용하여 positive sample을 따로 분류하여 학습하는 방법을 이용합니다. 하지만 IoU는 bbox의 크기에 따라 민감도가 다르다는 문제점이 있습니다. 큰 크기의 박스에 비해 작은 크기의 박스인 경우, 작은 움직임에도 낮은 IoU를 보일 수 밖에 없습니다. 그렇기에 약간의 오차에도 낮은 IoU를 갖기에 positive sample로 구성되기 힘들다는 문제가 있습니다. 즉, 학습 샘플로 학습될 가능성이 현저히 낮다고 볼 수 있습니다.
또 다른 문제는 default boxes는 휴리스틱한 방법으로 사전 정의됩니다. default boxes에 대한 사전 정의는 생각보다 성능 변화에 큰 영향을 줍니다. 예를 들자면 KAIST에서 KAIST에 맞게 튜닝된 Half-way와 기존 SSD의 default boxes를 가진 Half-way의 성능 차이를 볼 수 있습니다.
FCOS는 default boxes~anchor box로 발생하는 문제를 해결하기 위해서 anchor box를 사용하지 않고 다이렉트하게 bbox를 예측하는 방법을 제안합니다.

해당 방법론의 모티브는 생각보다 단순합니다. FCN(fig 1)은 semantic segmentation의 대표적인 방법론으로 각 픽셀 별 직접적으로 분류를 수행하는 방법으로 방법론 발표 당시에 높은 성능으로 센세이션을 일으킨 방법론 입니다. 다른 비전 태스크(e.g. Keypoint detection, depth estimation, counting …)에서는 FCN에 영감을 얻어 효과적이면서도 정확한 결과를 보여주었습니다. 근데!!! 물체 검출에서는 왜 적용하지 못하고 오히려 복잡하고 제약이 있는 default boxes를 사용하는 방법론만 있느냐!! 물체 검출도 가능하지 않겠느냐!! 가 모티브입니다.
위에서 말한대로 FCOS는 default boxes 없이 FCN처럼 다이렉트하게 bbox를 예측하는 방법에 대해 제안합니다.
Method

Fully Convolutional One-Stage Object Detector
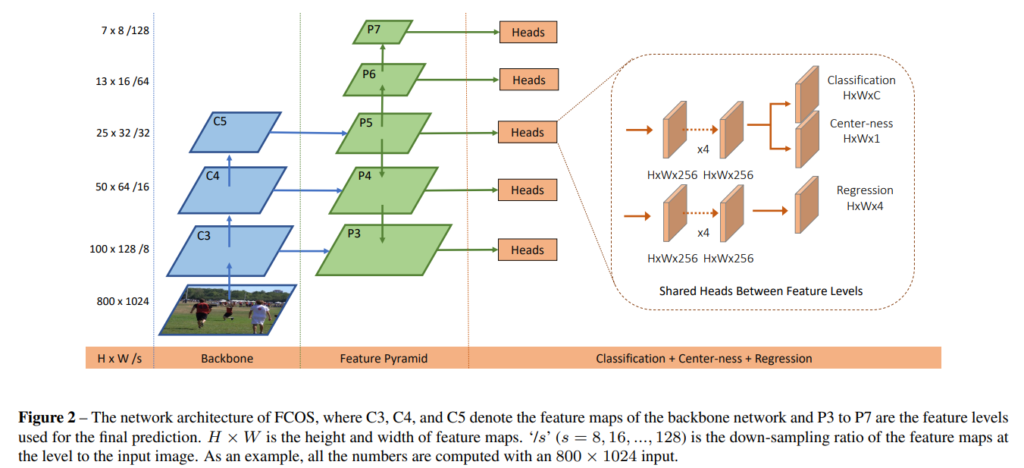
FCOS의 근본적인 구조는 기존 검출기와 유사합니다. 기존 검출기와 동일하게 각 feature map의 개별적인 위치 (x, y)에서 bbox의 offset과 해당 bbox에 대한 class를 예측합니다. 기존 검출기와 다른 점은 앞서 설명한 바와 같이 default boxes를 사전에 정의하지 않고 각 위치에서 다이렉트하게 예측을 수행하는 점입니다. 또한, IoU를 이용하여 positive sampling을 수행하지 않는 점입니다.
저자는 아주 간단한 트릭으로 default boxes를 사용하지 않는 방법을 제안합니다. GT에 개별적인 위치 (x, y)가 속한다면 예측된 class label을 활용하고 positive sample로 취급합니다. 속하지 않는 경우에는 negative sample로 간주하고 class label을 백그라운드(c=0)로 예측합니다. 이때 bbox의 크기를 예측하기 위해 (x, y) 기반으로 bbox의 거리 값인 (l, t, r, b)를 사용하여 bbox를 회귀합니다. 수식 1은 (l, t, r, b)은 아래의 수식 1에서 구할 수 있으며, (x_0, y_0, x_1, y_1) 은 bbox의 좌측 상단과 우측 하단의 좌표를 의미합니다. i는 layer를 의미하며 쉽게 풀자면 head를 의미합니다. 이에대한 예시는 fig 1에서도 확인할 수 있습니다.
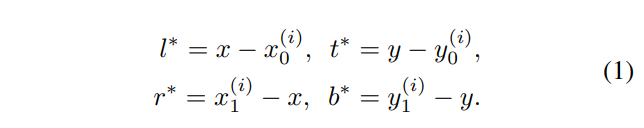
하지만 fig 1의 오른쪽 그림을 보면 같은 위치에서 크고 작은 박스들이 중복되어 예측되는 경우가 있습니다. 해당 케이스는 multi-level prediction을 사용하면 아주 간단하게 해결됩니다. 각 layer에서 bbox의 크기가 가장 작은 경우만 사용하면 해결됩니다.
+ 해당 부분은 SSD가 low-level에서는 상대적으로 작은 크기의 물체를 검출하고 high-level에서는 큰 크기의 물체를 검출한다는 점을 상기하시면 이해하시는데에 도움이 되실겁니다. 즉, high-level에서는 작은 크기는 무시된다는 가정 하에 사용할 수 있는 트릭 입니다.
Network Outputs. (COCO 기반) 최종적으로 FCOS는 num of classes (80D) + bbox에 대한 4D vector (l, t, r, b)를 출력합니다. 해당 방법론에서는 multi-classifier가 아닌 클래스 수 C 만큼의 binary classifier를 두고 예측을 수행합니다. 더 나아가 regression target이 항상 양수를 가질 수 있도록 exp을 적용하여 사용합니다. 즉, (x, y)에서 n 개의 anchor boxes를 사용하는 앵커 기반의 비해 배로 낮은 출력값을 가집니다.
Loss Function. Loss는 classifier loss에서는 focal loss를 사용하며 regression loss는 IoU loss를 적용합니다. indicated function은 negative sample인 background 클래스를 제외하고 학습하는 역할을 수행합니다. 이에 대한 수식은 아래의 수식에서 확인 할 수 있습니다.
+ p는 class score입니다.
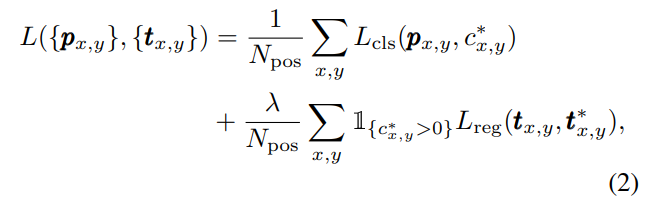
Multi-level Prediction with FPN for FCOS
FOCS에서는 FPN을 활용하고자 했습니다. FPN을 적용하기 위해서는 2가지 문제점이 있습니다. 1) stride가 크면 recall이 낮아질 수 있는 문제점과 2) GT가 겹칠 때, 모호함이 발생할 수 있다는 점입니다. 먼저, 1) 이슈인 경우, stride가 넓어 질 수 록 디테일한 스케일을 보지 못하는 것과 동일하기 떄문에 recall이 감소합니다. 앵커 기반의 검출기인 경우 IoU의 임계값을 낮추면 recall이 줄어드는 문제를 해결 할 수 있습니다. 반면에 FCOS에서는 IoU를 사용하지 않을 뿐더러 다양한 후보 박스가 없기 때문에 문제가 발생 할 수도 있습니다만, 이는 multi-scale을 가진 feature을 사용한 경우에 해당 문제가 해결됩니다. 해당 케이스는 실험적으로 검증을 진행했기에 아래에서 다시 다루도록 하겠습니다.
두번쨰 이슈인 GT가 겹칠 때, 발생하는 모호함입니다. 이는 앞서 설명하기도 한 fig 1의 오른쪽 케이스에 해당합니다. 즉, 앞서 설명한 바와 같이 서로 다른 스케일을 예측하는 feature maps에서 bbox를 예측하면 되기 때문에 이에 대한 문제가 해소됩니다. 구체적으로 max(l, t, r, b) > m_i or max(l, t, r, b) > m_i-1로 범위를 지정하여 각 할당된 feature map에서 예측할 bbox의 크기를 제약해줍니다. 만약에 제약 조건에도 겹치는 정보가 발생한다면 가장 작은 크기를 가진 타겟을 선정합니다.
+ m_2, m_3, m_4, m_5, m_6 -> 0 64 128 256 512 inf에 해당합니다.
Center-ness for FCOS
앞선 내용들로 FCOS는 앵커 없이도 예측이 가능해졌습니다. 하지만 저자는 저조한 성능을 가진 결과를 얻었다고 합니다. 분석 결과, low-quality prediction boxes가 너무 많아 학습을 방해하기 때문에 발생했다고 합니다. FCOS에서는 positive sample을 생성하기 위해서 GT 박스 내부의 (x, y)는 모조리 positive sample로 가정하는 방법을 취했습니다. 박스 내에 물체가 없을 수 있는 모서리와 같이 배경에서도 박스를 예측을 수행함으로써 low-quality prediction boxes가 생성되는 문제가 있었습니다. 저자는 이런 문제를 해결하기 위해 추가적인 하이퍼 파라미터 없이 재밌는 트릭을 사용합니다.

박스 내부에서 물체가 위치할 가능성이 높은 곳은 어디일까요? 아마 박스 가운데에 물체가 위치할 가능성이 높습니다. 저자는 박스 가운데에 물체가 있을 거라는 가정에서 모티브를 얻어 center-ness를 활용하고자 합니다. center-ness는 fig 2에서 보이는 바와 같이 classification branch로부터 single layer로 구성됩니다. 해당 값에 대하 GT는 아래의 수식을 생성되어집니다.
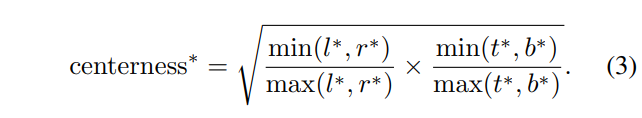
위의 수식에서 center-ness는 0-1의 범위를 가집니다. 그렇기에 해당 값은 BCE loss를 이용하여 학습이 진행되어집니다. final score는 center-ness * class score에 의해 sorting이 이뤄집니다.
이로써, NMS 수행 시에, bbox의 중앙과 멀리 떨어져서 위치를 추정하는 박스~low-quality prediction boxes를 높은 확률로 필터링 할 수 있게 됩니다.
Experiment
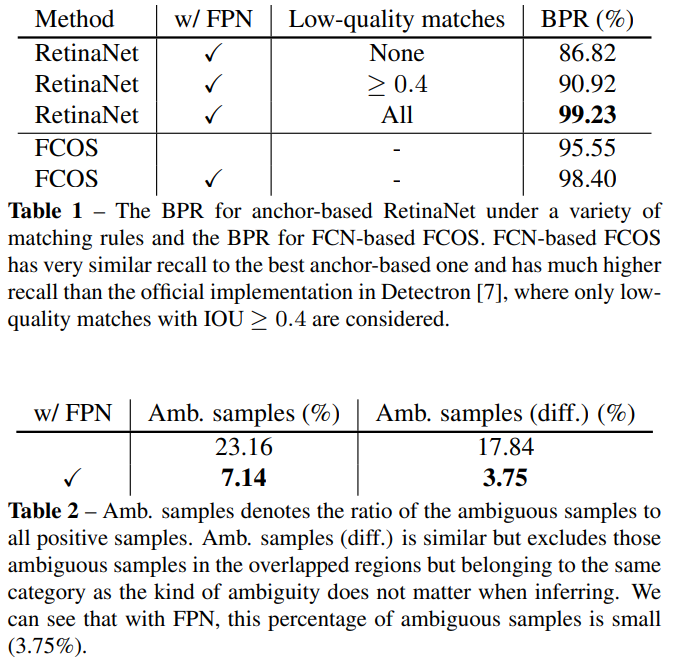
Tab 1은 recall이 떨어지는 문제를 해결하기 위해 FPN(multi-level prediction)을 사용하면 해결된다는 주장을 뒷받침하는 실험입니다. BPR은 best posible recall로 가장 좋은 결과를 리포팅하는 메트릭으로 이해하시면 됩니다. 실험 결과, FCN을 사용하는 앵커 기반인 검출기인 RetinaNet에서는 default boxes와 IoU 조절할 수 있기에 높은 BPR을 가지는 결과를 보여줍니다. FCOS에서는 Default boxes와 IoU를 사용하지 않고도 주장한 바와 같이 앵커 기반의 검출기와 유사한 성능을 보여줍니다.
Tab 2는 모호한 샘플에서의 강인성을 평가하는 결과 입니다. 저자의 주장대로 FPN을 사용한 경우에 모호한 케이스가 굉장히 많이 줄어드는 결과를 보여줍니다.
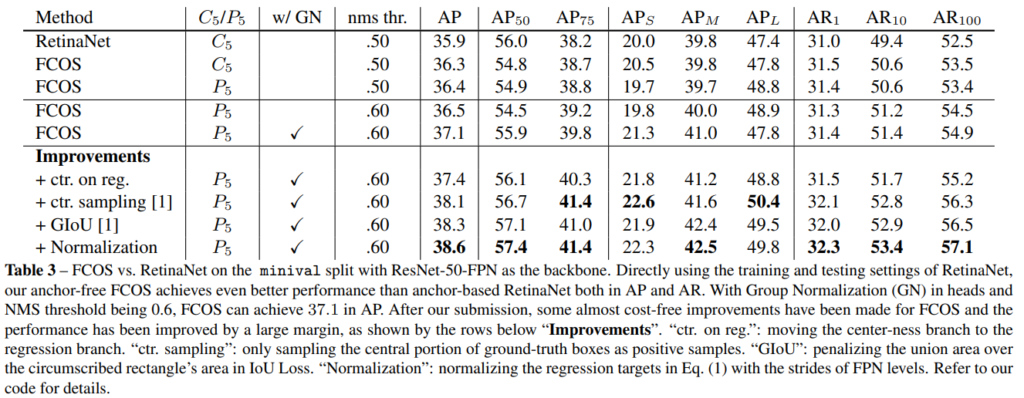
GN은 Group Normalization이며 ctr. on reg.은 centerness가 높은 지점에서의 regression을 수행한 결과에 해당합니다. ctr. sampling은 GT에서의 중심만을 positive sample로 사용한 결과, GIoU는 IoU loss를 GIoU loss로 변경한 결과
+ Normalization: normalizing the regression targets in Eq. (1) 라며 자세한 내용은 코드를 참고하라네요.. 시간될 때 자세한 내용 추가하도록 하겠습니다.
실험적인 결과, 앵커 기반의 방법론을 우회하는 결과를 보여줌으로써, 앵커 프리 기반의 가능성을 보여줍니다.
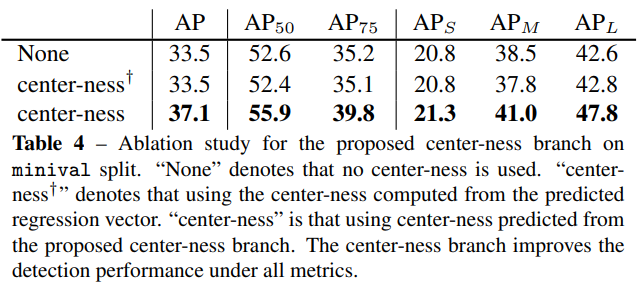
Tab 4에서는 center-ness의 효과를 입증하는 실험입니다. 확실히 사용했을 때, 높은 성능 향상을 보여줍니다.
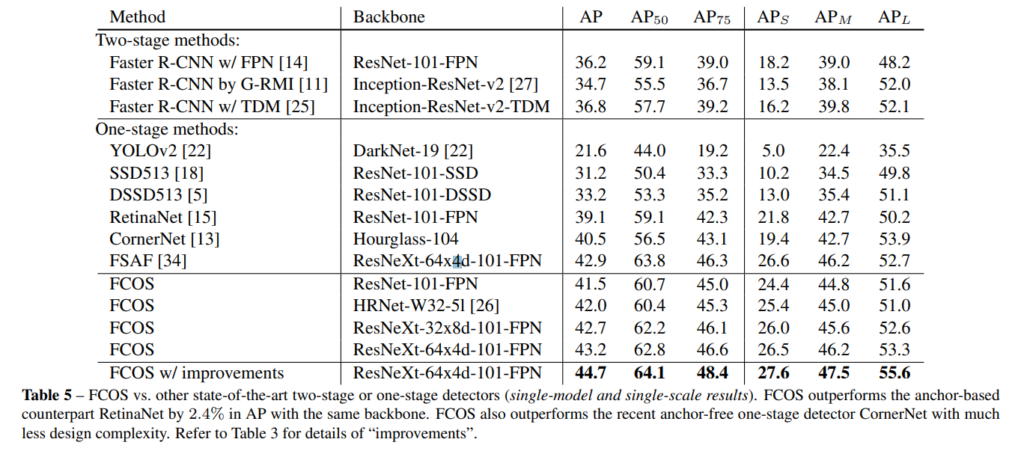
해당 실험에서는 SOTA 모델과의 비교 실험에 해당합니다. 가장 높은 성능을 보여줍니다.
갑자기 앵커 프리 방법론을 리뷰한 이유는 이번년도 한전 과제에서 small object detection을 요구하기 때문에 읽게 되었습니다. 그리고 사실 앵커 프리 방법론이 앵커 기반 방법론보다 우월하다고 보기에는 어렵습니다. 현존하는 방법론들이 여전히 앵커 기반을 이용한다는 점에서 알 수 있죠. 그렇지만 small object detection에서는 앵커 프리 방법론이 두각을 드러내고 있고 논리적으로 설득력이 강하기 때문에 앵커 프리 방법론 근본인 FCOS를 읽게 되었습니다.
리뷰 후, 앵커 프리의 가능성을 더욱 보게 되어 아마 이후 설계할 멀티스펙트럴 검출기는 앵커 프리 방법론으로 구성할 것 같습니다.
좋은 리뷰 감사합니다. 굉장히 흥미로운 논문이었습니다.
앵커 프리 기반은 대부분 저 centerness 아이디어를 가져가는 것 같아 신기하네요.
몇 가지 궁금한 점이 있어 댓글을 남기려고 합니다!
1. 김태주 연구원께서는 small object의 민감한 IoU로 인해 small object가 제대로 검출되지 않는 것을 문제로 정의하고, 해당 논문을 리뷰하신 것 같습니다. 그런데 small object의 경우, 작은 움직임에도 낮은 IoU를 가진다는게 저는 약간 헷갈려서, 추가 설명을 해주신다면 도움이 될 것 같습니다. 큰 물체와 작은 물체가 동일한 픽셀로 움직였을 때, 작은 물체의 IoU가 큰 물체에 비해 훨씬 작아진다는 뜻일까요?
2. 많은 앵커 프리 기반 방법론 중 해당 논문을 선정하신 이유가 있을지 궁금합니다! 사실 해당 논문 말고도 다양한 최신 앵커 프리 기반 방법론이 있는데 궁금해집니다!
1. 김태주 연구원께서는 small object의 민감한 IoU로 인해 small object가 제대로 검출되지 않는 것을 문제로 정의하고, 해당 논문을 리뷰하신 것 같습니다. 그런데 small object의 경우, 작은 움직임에도 낮은 IoU를 가진다는게 저는 약간 헷갈려서, 추가 설명을 해주신다면 도움이 될 것 같습니다. 큰 물체와 작은 물체가 동일한 픽셀로 움직였을 때, 작은 물체의 IoU가 큰 물체에 비해 훨씬 작아진다는 뜻일까요?
A. 넵. ‘큰 물체와 작은 물체가 동일한 픽셀로 움직였을 때, 작은 물체의 IoU가 큰 물체에 비해 훨씬 작아진다는 뜻일까요?’ 이 말이 맞습니다. IoU는 면적 대비 겹치는 영역을 의미합니다. 작은 물체인 경우, 한 픽셀만 어긋난다면 면적 대비 많이 벗어나기 때문에 큰 물체보다 큰 폭으로 떨어진 IoU를 가지게 되겠죠.
2. 많은 앵커 프리 기반 방법론 중 해당 논문을 선정하신 이유가 있을지 궁금합니다! 사실 해당 논문 말고도 다양한 최신 앵커 프리 기반 방법론이 있는데 궁금해집니다!
A. 해당 논문이 최초로 제안한 논문이라 읽어 봤습니다. 흥미를 이끌 논문이 있다면 한번 읽고 리뷰 하도록 할게요.