이번에 소개드릴 논문은 2018 NeurIPS에 나온 논문으로 꽤나 옛날 논문을 가져와봤습니다. 해당 논문은 Image matching 분야로 두 영상 간에 대응점을 잘 뽑아보자는 논문입니다. 최근에 Image Registration 쪽 연구를 하다보니깐 이런 쪽에 논문을 한번 읽어보게 되네요.
참고로 해당 논문은 Neighbourhood Consensus라는 개념을 처음으로 딥러닝에 접목한 논문이며 해당 논문을 시작으로 최근까지 관련된 방향의 방법들이 제안되고 있습니다. 그래서 최근 논문을 읽기 전에 해당 논문을 먼저 읽어보면 좋을 것 같아서 리뷰를 진행하게 됐습니다.
그럼 시작합니다.
Intro
두 영상 간에 대응점 또는 대응되는 영역들을 찾는 것은 정말 다양한 vision task에서 필요로 하고 관심 있어 하는 분야입니다. 가장 대표적으로는 3D reconstruction, visual localization, object recognition, image registration 등등이 있겠네요.

출처: https://www.youtube.com/watch?v=6j6NqAmR5ig
근데 이러한 visual correspondence task에서 어려워하는 점이 크게 4가지 정도 있는데 바로 1) Illumination Change, 2) repetitive texture, 3)Large view point change 4) Intra Class variation입니다. 즉 영상의 illumination 정보가 바뀌거나 또는 동일한 패턴들이 자주 발생한다던지, 또는 semantic 정보는 동일하지만 instance 레벨에서는 동일하지 않는 경우 등에 대해서도 명확하게 구분해서 대응점을 매칭해야 합니다.

출처: https://www.youtube.com/watch?v=6j6NqAmR5ig
여기서 저자는 위와 같은 매우 어려운 상황에 대해서도 잘 동작할 수 있게끔 neighbourhood consensus라는 개념을 모델링한 네트워크를 설계하고자 합니다. 여기서 neighbourhood consensus라는 개념이 상당히 중요한데 이는 어떠한 대응되는 포인트들이 있다면, 그 포인트들 주변 이웃 포인트들 역시 유사하게 대응이 되어야 한다는 원칙인 것 같습니다.
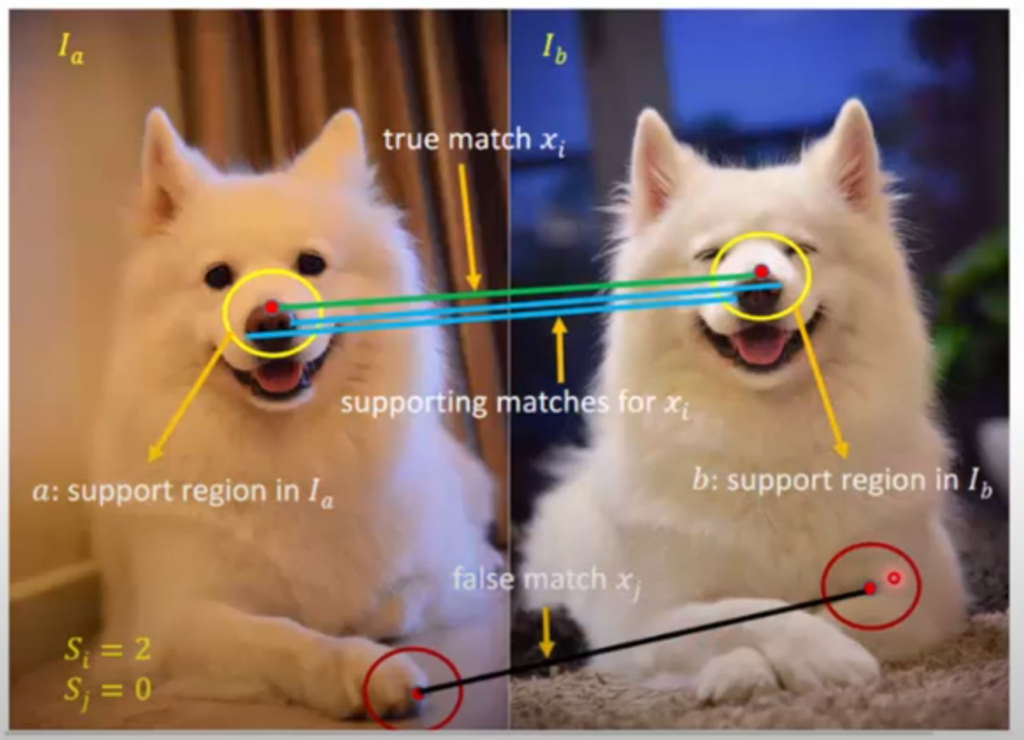
그림3을 살펴보시면 두 영상 속에 있는 동일한 강아지에 대하여 코 지점 붉은 포인트가 서로 대응되고 있습니다. 여기서 좌측 영상 붉은색 점 주변 이웃 픽셀들 중 2개의 파란색 포인트는 당연히 우측에 대응되는 붉은 색 포인트 점 주변 이웃 픽셀들과 대응이 되어야 할 것 입니다.
또 다른 예시로 좌측 영상에 강아지 앞발에 붉은 색 점이 우측 영상 강아지의 몸과 발 사이?에 매칭이 되어 있는 것을 볼 수 있습니다. 이것은 잘못 매칭된 상황인데 이 경우에는 당연히 주변 이웃 픽셀들 역시 매칭되는 지점들이 없게 됩니다.
아무튼 이러한 neighbourhood consensus 조건을 모델이 잘 학습할 수 있게 된다면 더 좋은 매칭 포인트를 예측할 수 있지 않을까 라는 것이 저자의 생각이며 이러한 관점에서 저자는 5개의 단계로 구성된 새로운 framework을 제안합니다.
Method
먼저 해당 논문에서 제안하는 framework의 overview는 아래와 같습니다.
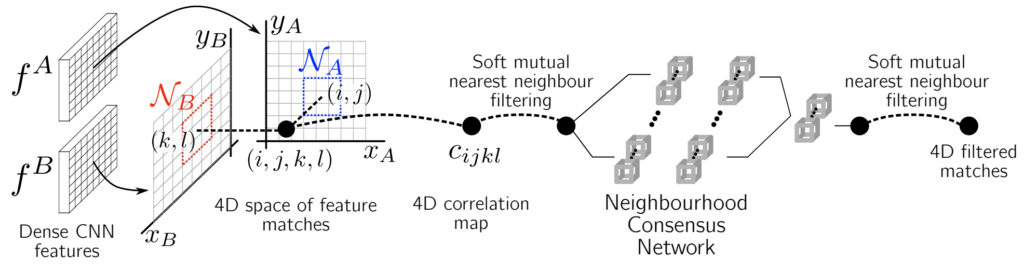
먼저 첫번째 단계는 두 영상에 대해 각각 CNN을 태워서 어떠한 feature map A와 B를 생성합니다. 참고로 논문에서 활용한 네트워크는 Resnet101입니다.
그리고 두번째 단계로는 4D space 상에 feature mathing을 수행하는 것입니다. 이 부분에 대해서 갑자기 4D가 튀쳐나와 벌써부터 머리가 어질어질 나는 포기할래 라고 생각하실 분들도 있을텐데 걱정 마십시오. 이 4D feature matching map은 이름만 거창하지 사실 A, B 두 feature map에 대한 correlation map을 의미합니다.
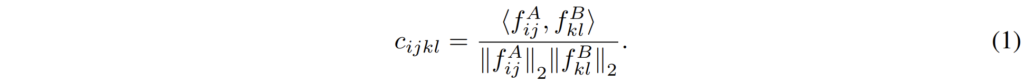
위 수식1번과 같이 두 feature map에 대하여 cosine similiarity를 계산하면 4d feature matching map을 계산할 수 있는데, 조금 더 이해하기 쉽게 shape으로 설명하자면 f^{A}, f^{B} 는 둘다 [B, C, H, W]의 shape을 가지게 됩니다.
이 때 [H*W, C] @ [C, H*W]와 같이 행렬 연산을 수행하게 되면 결과 값이 [H*W, H*W]가 되고 이를 reshape하면 [H, W, H, W]로 표현이 가능합니다. 즉 4차원으로 표현할 수 있기 때문에 4D feature matching map이라고 한 것이지 사실 상 두 영상에 대한 유사도를 계산한 correlation map을 의미합니다.
Neighbourhood consensus network
자 이전까지는 상당히 간단하였고 사실 여기부터 이제 해당 논문의 메인 파트입니다. 어떻게 하면 Neighbourhood consensus 조건을 판단할 수 있는 네트워크를 만들 수 있을까요? 사실 이 부분도 개념 자체는 심플한데, 아까 위에서 구한 4D correlation map에 대해 4D convolution layer를 태워주면 된다고 합니다.
이는 4D space 상에서 correlation 또는 matching pattern이 어떠한 translation을 했다 하더라도 결국 주변 이웃 픽셀들은 모두 동일한 correlation의 값을 유지할 것이기 때문에, Convolution의 연산이 그 성질과 잘 맞아떨어진다고 합니다. 음.. 그러니깐 결국 2단계에서 구한 correlation map에 대하여 더 좋은 표현력을 가지는(아마도 Neighbourhood consensus한 성질을 잘 나타내는) 4d correlation map을 생성하기 위해서 convolution 연산을 수행했다고 받아들여집니다.
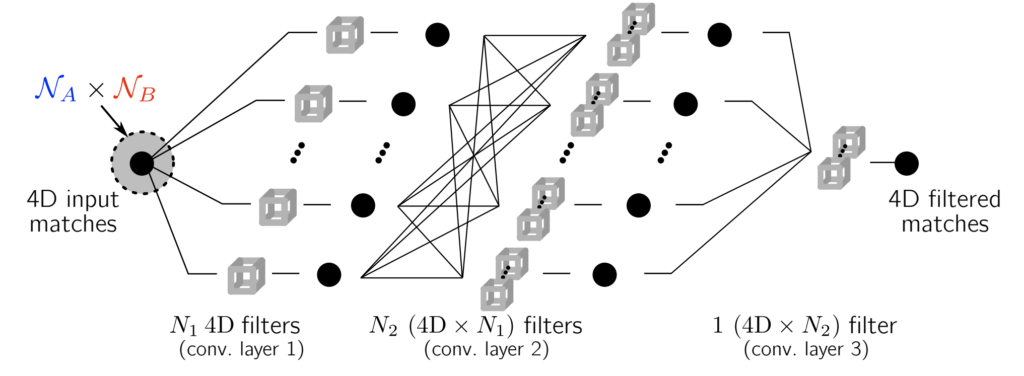
그럼 4D convolution을 어떻게 수행하면 될까요? 저도 이 부분에 대해서 코드를 직접 돌려보지는 못했지만, 얼추 여기 설명된 그림과 공개된 코드를 가볍게 살펴보니 채널 축에 대해서 3D 컨볼루션을 반복해서 돌리더라구요? 즉 필터 개수에 맞게 반복해서 3D 컨볼루션을 돌리는 것으로 판단되어지는데… 이 부분은 정확하지 않으니 너무 신뢰하지는 말아주세요ㅎ..
아무튼 이렇게 4D convolution을 태우는 것에 있어서 아래 수식과 같이 총 2번 입력으로 하여 최종 correlation map을 계산하게 됩니다.
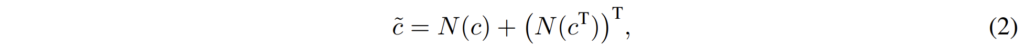
여기서 c는 2단계에서 feature map에 cosine similiarity로 계산한 correlation map을 의미하며, N은 4D conovlution Network를 나타냅니다. 이렇게 2번 연산하는 것은 correlation map이 현재 c의 경우에는 A feature에 대한 B feature의 correlation 값을 의미하며, c^{T}는 B feature에 대한 A feature의 correlation 값을 나타냅니다.
즉 방향이 서로 반대가 된다 하더라도 결국 동일한 대응 관계를 가질 수 있도록 이렇게 두번 태운 결과를 최종 correlation map으로 놓게 되는 것이죠.
Soft mutual nearest neighbour filtering
이렇게 4d convolution network를 태우게 되면 correlation map이 semi-local level에서는 잘 학습하게 되지만 global한 level에서의 표현력에 대해서는 어떠한 제약 조건이 부재하게 됩니다. 그래서 저자는 soft mutual nearest neighbour filtering이라는 것을 새롭게 제안하였는데, 여기서 mutual nearest neighbour filtering에 대하여 먼저 설명하겠습니다.
mutual nearest neighbour filtering의 목표는 간단합니다. 여기서 nearest neighbour는 제가 이해했을 때 단일 영상 내부에 어떠한 주변 이웃 픽셀의 개념이 아닌 두 영상 쌍에 대하여 가장 correlation이 높은 지점을 의미하는 듯 합니다.
즉 두 영상 사이에서 가장 높은 대응성을 가지는 지점(mutual nearest neighbour)는 살리고 그렇지 못한 matching case는 제거해버리자는 것이 해당 단계의 목표인 것이죠.
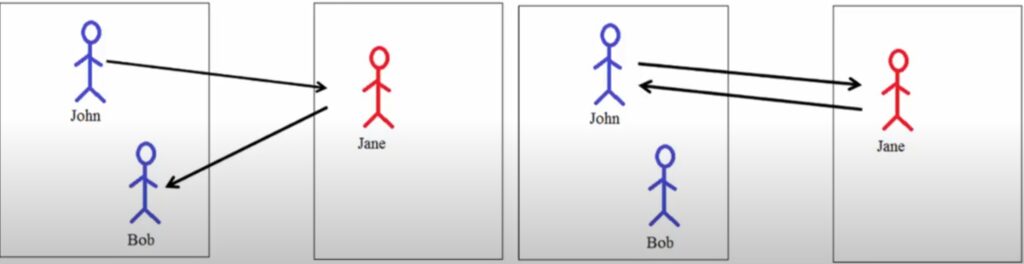
그림6을 살펴보시면 좌측 그림에 존과 밥이 있습니다. 그리고 우측 영상에는 제인이 있구요. 사실 이건 그냥 예시라서 이름에 신경쓰실 필요는 없습니다. 아무튼 좌측 상황에서 존에 해당되는 지점은 제인에 해당하는 지점을 가리키고 있습니다.
하지만 제인의 지점은 존이 아닌 밥을 가리키는 것을 볼 수 있습니다. 이러한 상황은 두 지점간에 correlation이 낮다는 것을 의미하며, 엉뚱한 matching임을 알 수 있습니다. 즉 이러한 경우는 필터링해서 제거해야겠죠.
우측 상황에 대해서도 살펴볼까요? 우측에서는 존과 제인이 서로를 가리키면서 두 지점 모두가 올바르게 매칭되는 것을 알 수 있습니다. 이러한 상황을 mutual nearest neighbour라고 하며 이러한 상황은 제거하는 것이 아닌 잘 보존하는 것이 중요하겠습니다.
아무튼 이러한 내용들을 수식적으로 표현하게 되면 다음과 같습니다.
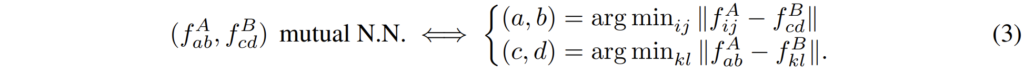
A feature map에 (a, b)라는 지점과 B feature map에 (c, d)라는 지점이 서로 mutual nearest neighbour라고 한다면, (a, b) 지점에 해당하는 것은 f^{A}_{ij} - f^{B}_{cd}를 하였을 때 가장 작은 값을 가져야만 할 것입니다. 그리고 (c,d)도 그 반대로 진행되겠구요. 여기서 i,j와 kl은 각각 A와 B feature의 전체 픽셀을 의미합니다.
아무튼 이러한 hard decision의 경우에는 가장 작은 값을 선택을 해야하는 것이기 때문에 사실 미분이 안됩니다. 그래서 저자는 어떻게 하면 미분이 가능하도록 할 수 있을까 고민을 하였고 결국 아래와 같은 방식을 통해 soft한 방식을 제안합니다.
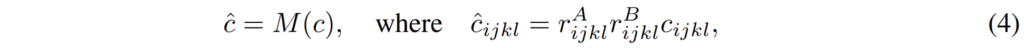
여기서 M은 mutual nearest neighbour filtering을 soft하게 바꾼 함수를 의미하며 실제 구현은 r^{A}_{ijkl}*r^{B}_{ijkl}*c_{ijkl}로 나타냅니다. 여기서 r은 매칭 스코어의 비율을 의미하는데 이는 아래 수식(5)와 같습니다.
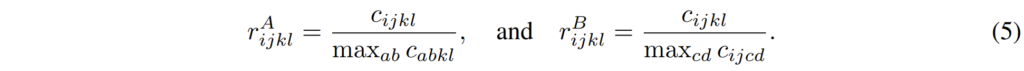
갑자기 막 기호로 도배가 되니깐 어렵다고 느끼실 수 있는데 제가 위에서 설명드린 mutual nearest neighbour filtering을 제대로 이해하셨다면 이 부분도 상당히 간단합니다. 저희가 아까 (a,b)와 (c,d)가 서로 mutual nearest neighbour라는 가정이라면 전체 source feature map에 대하여 target feature map의 (c,d)지점과 차이를 계산하였을 때 가장 작은 값인 지점이 (a,b)라고 하였습니다.
이를 바꿔서 표현하면 (c,d)좌표에 대한 (a,b)의 correlation 값과 (a,b)에 대한 (c,d)의 좌표값이 또 다른 지점(예를 들어 (e,f)?)과 비교하였을 때 더 큰 correlation 값을 가질 수 밖에 없습니다.
즉 전체 i,j,k,l에 대하여 각각에 대한 correlation pair가 존재를 할텐데, 여기서 (a,b)와 (c,d) 서로에 대한 correlation 값이 전체 correlation matching pair들 중에 가장 큰 값을 가질 수 밖에 없다는 것이고, 관련이 없는 즉 mutual nearest neighbour가 아닌 쌍들 끼리는 correlation 값이 작게 나올 것입니다.
그렇기 때문에 (a,b)좌표가 있는 차원 기준의 max correlation값을 전체 correlation c_{i,j,k,l}에 대해서 나누게 되면 mutual nearest neighbour는 1에 가까운 값을 가지게 될 것이며 관련 없는 매칭들은 0에 가까운 값을 가지게 될 것입니다. (max normalization이라고 생각하시면 돼요.)
아무튼 이렇게 각각 A와 B에 대한 ration를 계산하고 이를 전체 correlation map에 곱해주게 되면 correlation score가 높은 케이스들 즉 mutual nearest neighbour들은 1에 가까운 값을 곱해져서 그대로 유지하게 되며 그 외에 관련 없는 값들은 0에 가까운 값에 곱해짐으로써 약해지거나 제거가 될 수 있는 것이죠.
Extracting correspondences from the correlation map
아무튼 이렇게 filtering까지 마치게 되면 최종적으로 저희는 잘 학습된 correlation map에 대하여 correspondence를 추출해야만 합니다. 즉 가장 correlation 값이 높은 case를 선택하면 되는 것인데, 먼저 softmax를 취함으로써 correlation score를 계산하게 됩니다.
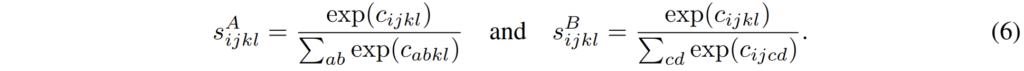
이렇게 score를 계산하는 것이 끝났다면 이제 해당 score가 가장 큰 값을 argmax를 통해서 가져오게 되면 최종적인 hard-assignment가 마치게 됩니다.
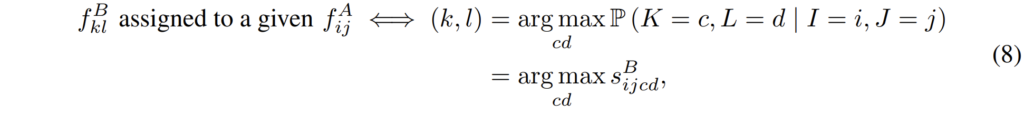
위에 수식에 대한 예시로는 A라는 feature가 주여졌을 때 이에 할당되는 feature B에 대하여 s^{B}_{ijcd} 중 cd 차원에서 가장 큰 값을 가진 지점이 i,j에 assign될 수 있는 지점이라는 것이죠.
Weakly-supervised training
다음은 모델을 학습시키기 위한 loss function에 대해서 알아보겠습니다. 참고로 기존의 visual correspondence task에서는 두 misalignment image 쌍에 대하여 사전에 알고 있는 homography나 camera pose 또는 실제 대응되는 pixel을 알고 있는, 즉 Ground Truth를 가진 상태에서 학습을 진행하는 것이 일반적이지만, 해당 방법론은 weakly supervised 방식으로 모델을 학습한다고 합니다.
그 이유는 misalignment가 발생한 영상 쌍에 대하여 대응되는 지점을 GT로 취득하는 것은 비용이 많이들며, 그렇다고 임의의 homography 등을 통해 정합이 깨진 합성 데이터를 생성하는 것은 실제 real한 환경에 대한 정보를 온전히 담지 못하기에 실제 데이터 셋에 대하여 성능이 감소한다고 합니다.
아무튼 저자가 제안하는 weak-level supervision 방식은 아래 수식과 같은데, 학습 때 positive pair와 negative pair에 대한 정보만 가지고 있따면 이에 대하여 loss가 적용되는 방식을 부호 변경을 통해 마치 contrastive learning처럼 학습하겠다는 것입니다.
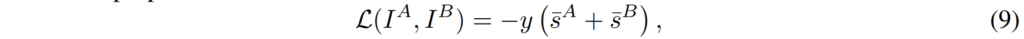
여기서 \bar{s}^{A}, \bar{s}^{B} 는 각각 수식 8을 통해 계산한 hard assigned matche의 mean matching score값을 의미합니다. 즉 postivie pair들끼리는 matching score 값이 유사하도록 학습이 진행되는 것이며, negative pair들끼리는 matching score값이 오히려 커지면 좋지 못하기 때문에 낮은 matching score를 가지도록 학습하는 것입니다.(y가 positive, negative 여부에 따라서 부호가 +, -로 바뀜.
Experiments
그럼 실험 섹션 빠르게 훑고 리뷰 마치도록 하겠습니다.
저자가 평가한 방식은 크게 2가지로 하나는 Category-level matching, 나머지는 Instance-level matching입니다. 둘의 차이를 쉽게 설명하기 위해 먼저 정성적인 결과부터 보여드리겠습니다.

그림 7의 좌측은 Category matching을, 우측은 Instance-level matching을 나타낸 것입니다. 딱 보시면 아시겠지만, Category matching은 대상은 다를지라도 동일한 class에 대하여 어느 지점이 대응되는지를 맞추는 분야입니다. 즉 왼쪽 이미지에서 고양이의 눈, 코, 귀에 대한 5개에 포인트를 주고 이와 대응되는 지점을 오른쪽 영상에서 맞춰보도록 모델에게 지시하는 것이죠.
반대로 Instance-level matching의 경우에는 따로 주어지는 포인트는 없으며 그냥 indor visual localization이라고 생각하시면 편합니다. 그냥 query 영상에 대하여 6DoF camera pose를 추정하는 task라고 볼 수 있는 것이죠.
물론 제가 소개드린 방법론은 Image retrieval 방법이 아닌 image matching 방법론이기 때문에, 저자는 candidate image를 생성하고자 DensePE와 InLoc이라는 방법론을 활용했다고 합니다. 그 후 저자가 제안하는 NC-Net을 통해 pose estimation을 계산하기 위한 correspondence를 계산한 것이구요.
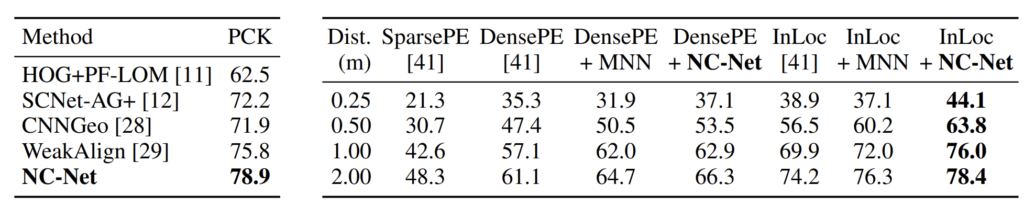
실제 정성적인 결과는 다음과 같습니다. 왼쪽은 PASCAL VOC 데이터 셋을 category matching task를 위해 재가공한 PF-Pascal dataset이며 우측은 instance-level matching taks를 위한 InLoC dataset입니다.
참고로 평가 지표에 대해서 각각 설명드리자면 PCK의 경우 percentage of correct keypoints의 약자로 annotation이 된 keypoint와 모델이 예측한 key point가 얼마나 잘 맞았는지에 대한 평균 값을 의미합니다.
그리고 indoor localization의 경우에는 10도의 angular error와 제일 좌측에 각각 0.25~2.00까지의 meter 오차에 대한 정답 비율을 평가로 나타낸 것입니다.
한계
사실 논문에는 해당 논문의 한계점이 명시되어있지 않지만, 이 논문에는 가장 큰 문제가 존재합니다. 바로 너무 많은 양의 메모리와 시간을 잡아먹는 다는 것입니다. 논문의 저자들도 이를 의식했는지 제가 리뷰한 논문에는 전혀 그런 내용이 없다가 2020 ECCV 논문을 제출할 때 자신들의 이전 논문이 겁나 느리고 메모리 많이 잡아먹는다며 열심히 까기 바쁩니다.
이게 아무래도 HxWxHxW의 correlation map을 계산하다보니 feature map의 해상도가 100×75만 된다 하더라도 추론 시 메모리가 5기가에 학습시에는 50기가를 잡아먹는다고 하더군요. 추론 속도도 10초정도 된다고 합니다.
물론 ECCV에서 새로 제안한 방법론은 메모리 사용량을 1기가 미만으로 줄이긴 했습니다만 tesla T4 GPU 기준 추론 속도가 1.56초가 되네요.. 아무래도 성능은 좋지만 실시간 추론으로 사용하기에는 무리가 있는 방법인 것 같습니다.
물론 22년도에 제안된 Neighbourhood Consensus 기반 방법론들은 더욱 빠르면서 정확한 방법론이 나왔을지도 모르겠습니다만.. 아무튼 참고하시면 좋을 것 같습니다.
결론
제가 리뷰에다가는 내용들이 간단하다는 식으로 작성해놨지만 사실 4D convolution이니 뭐니, argmax는 또 뭐이리 많이 들어가는지 사실 이 논문을 읽으면서 여간 어려운 것이 한두가지가 아니었습니다. 논문만으로는 이해가 어려워서 저자가 유튜브에 올린 발표 영상도 계속 보고 논문도 또 다시 읽고 하다보니 하나 둘씩 이해가 가긴 하네요.
지금 논문 작성 중인 Multispectral Homography Estimation 분야가 마무리 된다면 추후에 어떤 연구를 계속 해야할지에 대한 걱정과 고민이 있어 견문을 넓혀보고자 한번 읽어보긴 했는데 상당히 좋은 내용이지만 제가 이쪽 분야에서 적응할지 잘 모르겠네요허허. 아마 해당 분야의 논문을 처음 읽다보니 그런거라 생각하고 이쪽 분야로 앞으로 조금 더 읽어볼 예정입니다.