Intro
본 논문은 labeled data가 매우 적은 상황에서 semi-supervised learning을 할 때 발생할 수 있는 문제점인 confirmation bias 문제를 해결하기 위한 논문으로, 해당 문제의 해결 필요성을 toy data와 cifar에 대한 실험을 통해 밝히고, propagation regularizer와 model selection method를 제안하여 이를 해결하고자 하였다.
Confimation bias
confimation bias란 모델이 부정확한 정보에 치중되어 옳은 정보를 오히려 무시하고 잘못된 학습을 강화시키게 되는 상황이다. 이는 labeled data가 충분하면 다양한 샘플을 학습하는 과정에서 자연스럽게 해결되지만 labeled data가 적을 경우는 발생하기 쉬우며 특히 pseudo-label과 같은 기법에서 자주 발생하는 문제이다.
[문제1: confimation bias] Analysis with Toy Examples
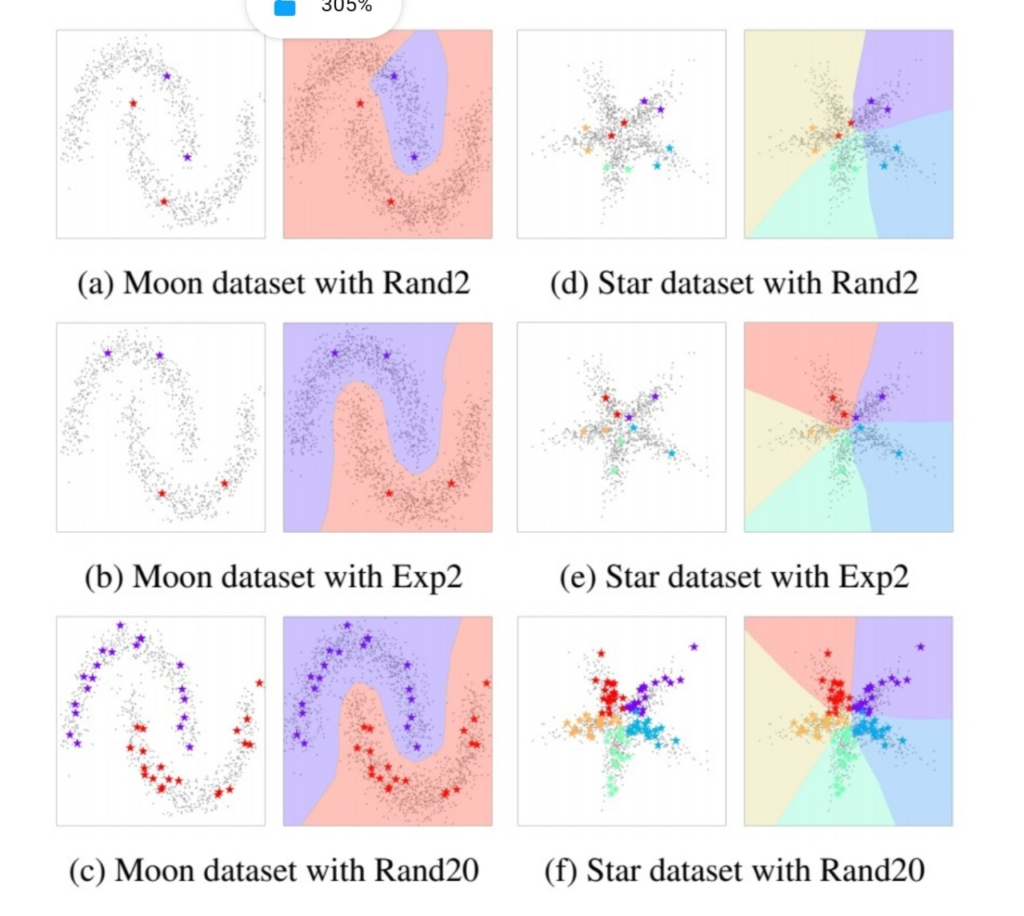
다음은 moon dataset, start data를 이용한 분석 결과이다. Rand{n}는 랜덤으로 선택한 n 개의 데이터를 labeled data 나머지는 unlabeled data로 사용하여 FixMatch 를 통해 학습 한 결과이며, Exp{n}은 전문가가 분포를 고려하여 선정한 n개의 데이터를 labeled data로 사용하고 나머지는 앞과 같은 방식으로 하여 학습한 결과이다. 보면 FixMatch(SSL 방법론을 대표하는)의 성능이 labeled data에 대한 의존성이 큼을 알 수 있다. labeled data의 갯수가 어느정도 보장되는 경우 (Rand20) 에는 잘 학습하였지만, labeled 데이터가 매우 부족한 상황에서 해당 샘플이 데이터의 전체 분포에 대한 대표성이 없다면 confirmation bias 현상이 발생하여 잘못된 결정 경계를 학습하고 있다.
[문제1: confimation bias] Analysis with real-world dataset(CIFAR-10)
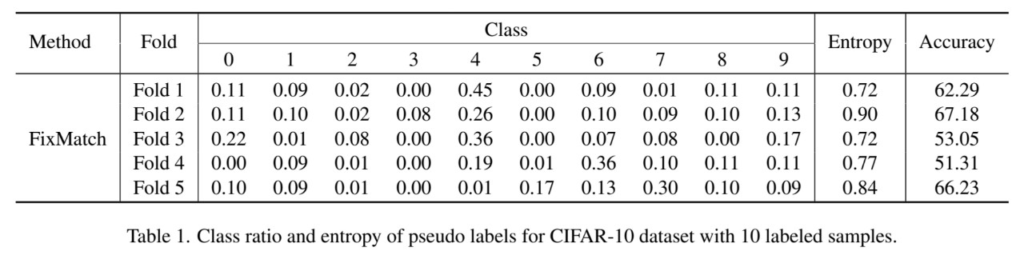
논문에서는 매우 적은 labeled data를 사용해 학습할 때 발생하는 현상을 조금 더 현실에 가까운 데이터를 통해 확인하기 위해 CIFAR10 데이터셋을 이용하여 추가 분석을 진행했다. class 당 단 하나의 데이터만을 labeled 데이터로 이용하여 Fixmatch 를 학습시켰고 유사한 셋팅으로 5번을 반복하여 실험했다(5 folds) 실험 결과는 위의 [표1]과 같다. 실험 결과를 보면 잘 학습된 경우(=Accuracy가 높은 경우) Entropy(클래스가 고르게 뽑히는 정도)가 1에 가까움을 확인 할 수 있다. 그러나 모든 반복 실험(fold)에서 class 당 pseudo label이 학습에 포함되는 경우 (즉 threshold에 의해 통과되는 경우)의 수가 고르지는 않음을 확인할 수 있다. 이를 통해 pseudo label로 포함되는 샘플의 클래스 분포가 고를 떄 더욱 학습이 잘 된다는 가설을 세울 수 있고, 이를 통해 해결하는 문제점이 confirmation bias 문제일 것이라는 가설을 세울 수 있다. 정리하면 분포를 잘 대표하는 labeled data를 선택해 학습할 수록 confimation bias 문제가 발생하지 않아 더 좋게 학습할 수 있다는 것이다.
[문제2: SSL의 불안정한 학습]
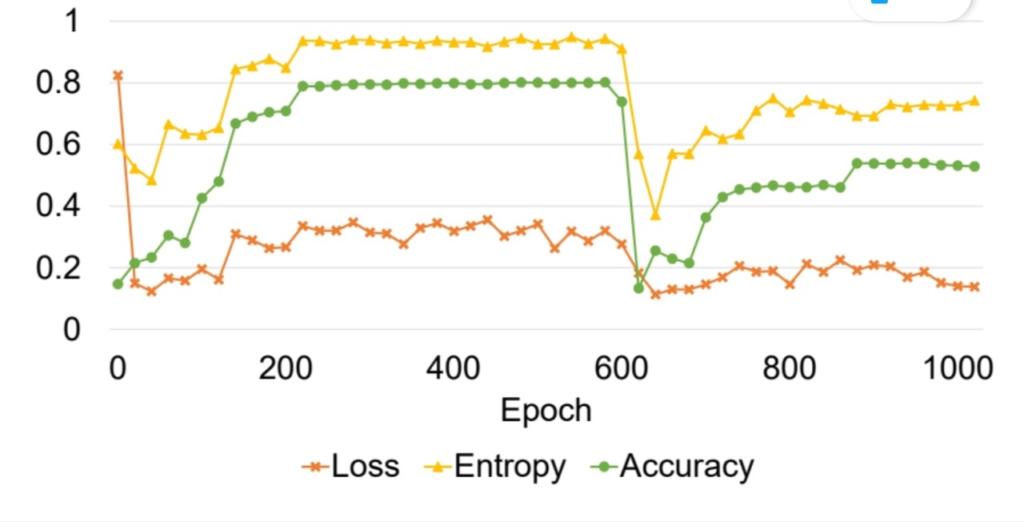
논문에서 주목한 문제가 하나 더 있는데 SSL 방법론의 불안전한 학습 문제이다. 위를 보면 SSL 문제의 학습이 loss가 계속 줄어들고 있더라도, 정확도가 중간에 크게 떨어지는 현상을 확인할 수 있으며, loss가 모델의 학습 정도를 어느정도 대표할 수 있던 기존 방법론과 다르게 SSL 방법론에서는 validation 과정이 필수적이다. 그러나 labeled data가 매우 적은 SSL 학습 과정 중 소중한 labeled data를 validation 과정에 이용하는것은 어려운 일이다. 따라서 본 논문은 이를 해결하기 위해 labeled data를 이용하지 않고 최적의 모델을 선정하는 model selection 방법론 또한 제안하였다.
[문제 1] 해결책: propagation regularizer
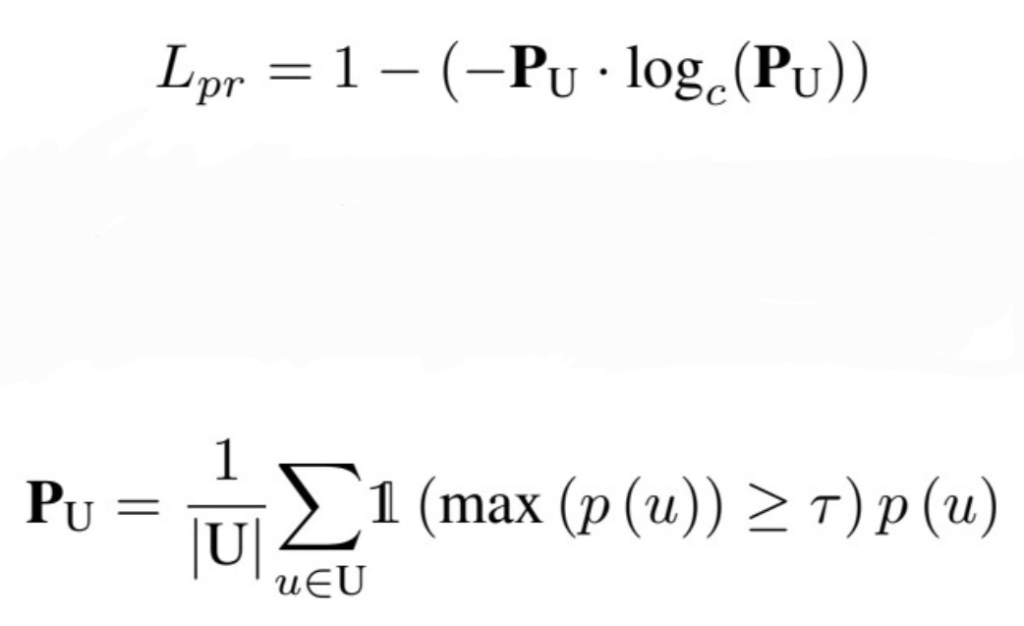
문제점 1의 해결책을 위한 loss는 [수식1]과 같다. Pseudo-labeling을 통해 선정되는 unlabeled data의 class 분포가 균등하게 되도록 정규화 loss를 구성한 것이다. unlabeled 의 분포가 완벽히 균등하면 해당 loss는 0이 된다. 해당 loss 는 기존의 SSL loss에 더해서 사용된다.
[문제 2] 해결책: model selection
논문에서는 좋은 모델을 unlabeled samples을 최대한 많이 활용하면서, confimation bias의 영향을 최대한 적게 받는 모델로 정의하였다. 정의에 따라 model selection을 위한 측정은 위의 두가지 요소를 고려하여 설계되었다. 먼저 unlabeled smaples을 최대한 많이 활용하기 위해 utilization measure을 정의하여 사용하였으며 모든 unlabeled data를 사용하면 1, 전혀 사용하지 않으면 0이 되도록 식을 설계하였다. (1/batchsize*sum(batch 내에서 학습에 사용되는 unlabeled data 갯수)) 다음으로 confimation bias 영향을 최소화하기 위한 정도를 측정하기 위해서는 위의 loss 식을 그대로 사용하였다. model selection은 모델 학습 시 사용하지는 않고 학습된 모델들 중에서, 최적의 model을 찾기 위해 사용된다.
실험
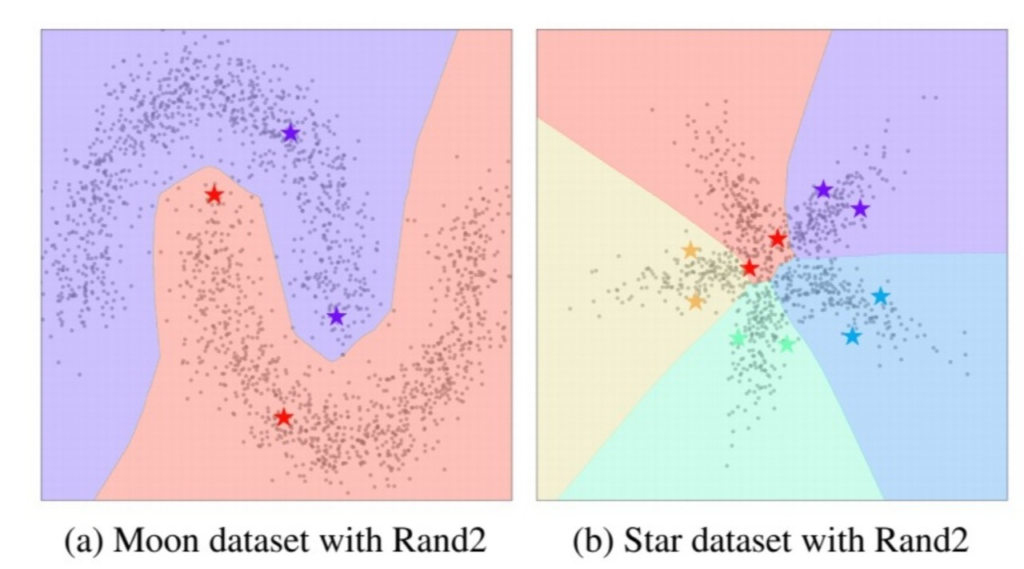
[그림3]은 앞선 [그림1]의 확장 실험으로 동일한 셋팅(Rand2)에서 제안하는 방법론을 적용하였을 때이다. 시작의 labeled data가 데이터셋 전체 분포를 대표하지 못하는것은 동일하지만, 제안하는 방법론을 통해 confirmation bias 문제 없이 잘 학습하였음을 알 수 있다.
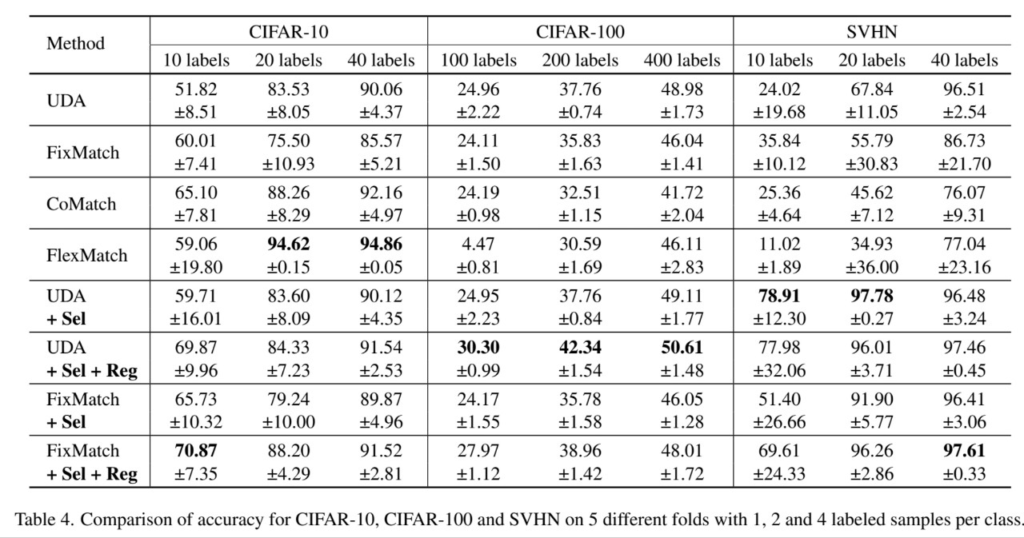
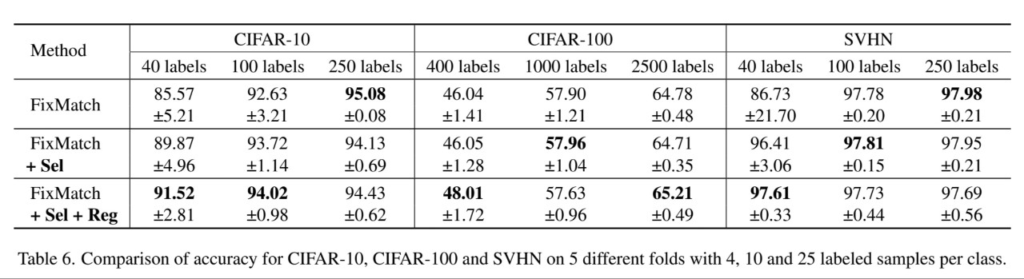
다음의 표는 기존 SOTA 방법론과의 비교이다. [표2]에서 확인할 수 있듯이 labeled 갯수가 매우 적은 (class 당 순서대로 1개, 2개, 4개)인 상황에서도 높은 성능을 보이며, CIFAR100에서 모든 경우에 SOTA 성능을 보이며 class 갯수가 많은 데이터에도 잘 적용됨을 알 수 있다. 또한 [표3]을 통해 비교적 많은 양의 labeled data를 사용할때의 성능도 보여, 제안하는 방법론이 언제나 잘 작동함을 보였다. 다만 제안하는 방법론을 적용하여 얻은 performance gain 정도가 줄었는데, 이는 방법론이 해결하는 문제인 confimation bias가 labeled data가 많을수록 약하게 발생하기 때문이라고 분석하였다.
좋은 리뷰 감사합니다. 몇가지 semi-supervised 방법론에서 발생할만한 문제점을 언급해주셨는데요. 그런데 혹시 저자가 왜 그런 문제가 발생하였는지는 밝히나요? 그리고 confirmation bias에 대해 정말 발생하는지 보여주는지도 궁금합니다.